基于岩石拉压宏观力学响应的平板模型微观参数匹配分析

成晨，林杭

(中南大学资源与安全工程学院，湖南长沙 410083)

在岩体工程的研究中，研究对象常常是一些大型的岩石构造体，如大型边坡稳定性分析，深部隧道开挖，地下开采等，这些工程很难通过室内试验进行研究。随着计算机技术的飞速发展，利用数值模拟可实现对岩体数值模型施加室内试验无法实现的复杂应力条件，因此该方法在岩体工程领域得到了广泛的应用。离散元法(DEM)是解决粒状和不连续材料工程问题的一种有效数值方法,常用于模拟岩石材料从微观破裂到宏观破裂的演化过程，可直观地展现材料的破坏行为以及裂隙的扩展[1]。利用颗粒离散元数值模拟研究岩体的力学性质时，需要进行全面的标定工作，标定过程包括变形和强度的参数修正。黏结的颗粒模型需要按照给定的材料确定的具体微观参数进行制备，以便再现特定的宏观材料性能，这一过程直接影响最终模拟结果的可靠性。另一方面，接触模型的选择也会影响微观参数匹配的效果和颗粒模型的宏观力学表现，所以数值模型的标定研究对岩石数值模拟试验有着重要意义。模型微观参数一般采用试错法或者反演计算法标定，该方法通常耗时费力并且盲目性大。因此，国内外学者对此进行了简化。POTYONDY 等[2]分析了颗粒与接触的微观变形强度参数对颗粒黏结模型双轴、三轴、巴西劈裂试验模拟结果的敏感性。YOON等[3-4]在使用PFC 模拟岩石单轴压缩试验时分别测试了线性平行黏结模型的微观参数对单轴抗压强度，杨氏模量和泊松比的敏感性，通过统计中央复合设计方法与Plackett-Burman(P-B)设计方法相结合应用计算机程序生成了最佳微观参数集。李坤蒙等[5]提出了基于物理试验响应的参数确定方法，利用物理试验响应反演计算颗粒间的接触本结构参数。邓树新等[6]利用P-B 设计和响应曲面法结合数学规划建立了平行黏结模型的接触模量，黏结强度等模型微观参数的标定方法。邓树新等[6]利用P-B设计和响应曲面法结合数学规划建立了平行黏结模型的接触模量，黏结强度等模型微观参数的标定方法。WANG 等[7]通过敏感性分析和全局优化过程来标定黏结离散元的宏观力学性能。POTYONDY[8]提出考虑颗粒的多边形结构的平板模型，用于取代平行黏结模型模拟典型硬岩，模拟结果表明平板颗粒黏结模型更加符合岩石破坏的微观和宏观机制。WU 等[9]基于黏结颗粒模型(BPM)的3 个内在问题，提出利用平板模型解决黏结颗粒模型的抗压拉强度比、内摩擦角的校正问题。上述研究在黏结颗粒模型微观参数对宏观力学参数的影响，以及接触微观参数标定方法上有较为丰富的成果，但存在以下问题：首先，多数岩石模型参数标定研究没有考虑岩石的抗拉强度，强度包络线等岩石力学宏观特性的校正；其次，目前大多参数标定是基于平行黏结模型，而平行黏结颗粒模型已被多数学者证实有抗拉强度失真的问题，能解决该问题的平板模型目前研究较少，其部分接触微观参数与宏观相应之间的的关系尚不明确，需要进一步研究。针对上述问题，本文采用Box-Behnken设计试验法，以多元线性模型拟合模拟结果，得到能够反映平板接触模型微观参数对宏观力学参数敏感性的关系方程，通过反解关系方程组，提出平板模型4个主要微观参数的算法方程。

1 数值模拟

1.1 模型选择

在PFC 软件内置的接触模型中，接触黏结模型(CBM)和平行黏结模型(PBM)常被用于模拟完整岩石，2 个模型的差异主要体现在力的相互作用和传递上。接触黏结模型只在颗粒接触点之间起作用而线性平行黏结模型是在接触面上通过以接触点为中心的有限矩形或圆盘横截面上活动，并且接触黏结模型只能传递力的作用，无法抵抗弯矩或者滚动，而线性平行黏结模型能够同时传递颗粒之间的力与力矩。当接触破坏时，线性平行黏结模型接触刚度能立即下降，而接触黏结模型的接触刚度则会一直保持作用。因为这些优点，目前许多模拟研究选择平行黏结模型来模拟完整岩体。而SHARRKOCK[10]对人造节理岩石的研究中明确指出，无论是对大尺寸试块还是小尺寸试块，平行黏结模型都无法实现对其抗拉强度的校准(模拟抗拉强度约是实际抗拉强度的5 倍)。为更好地解决拉压比的失真问题，POTYONDY[8]提出了考虑颗粒的多边形结构平板模型(FJM)，当颗粒相接触时，会产生一个抽象的接触表面，该接触面被离散化为元素并且可以产生相对旋转。接触面的每个元素都具有独立的状态。3 种模型黏结示意图见图1。吴顺川对平板模型材料的研究里证明了平板模型能够解决颗粒黏结模型的拉压比失真的问题，所以本文选择平板黏结颗粒模型作为主要研究对象。

图1 颗粒接触模型示意图Fig.1 Schematic diagram of particle contact model

1.2 模型建立

为获得模型宏观参数,首先需要建立一个与标准试验岩体样品尺寸相同的颗粒黏结模型(BPM)，参考POTYONGDY 等[2]的模型建立方法，首先生成颗粒体系、之后按顺序进行伺服压密、处理游离颗粒以及平衡系统等步骤(见图2)，最后建立如图3 所示的尺寸为φ50×100 mm3，共包含10 563 个圆形颗粒的颗粒黏结模型试样。

1.3 单轴压缩试验

试验加载前在模型中心设定一个测量圆，用于记录每个计算步数的横向应变速率与纵向应变速率以及材料中心的平均应力。接着给上下墙设置一个0.01 m/s的加载速率，通过记录上墙体收到的压力来记录模型受到的轴向应力，在瞬时轴向应力降为其峰值的70%时终止循环，输出计算过程中的轴向应力-应变曲线。模型的泊松比可由测量圆测得的横向应变速率比纵向应变速率计算得到。

1.4 直接拉伸模拟试验

直接拉伸试验模拟采用与单轴压缩实试验相同的材料模型，删除上部与下部墙壁，并将材料顶部和底部的一排颗粒设置为“抓手”(见图3)。顶部手柄向上以0.01 m/s的速度移动，同时底部手柄向下以相同的速度移动，以施加拉伸载荷。利用中心设置的测量圆的平均圆内接触力来计算模型中心拉应力。

图3 单轴压缩模拟试验与直拉模拟试验Fig.3 Uniaxial compression simulation experiment and direct tension simulation experiment

2 微观参数匹配

单元试件模型建立后，以试验获得的岩石宏观力学参数为依据，标定模型的微观本构参数。为解决颗粒黏结模型模拟岩石抗拉强度失真的问题，本文选取抗拉强度σt，单轴抗压强度σc，弹性模量E和泊松比λ作为宏观标定参数。

2.1 常规匹配流程

参考Gutiérrez-Ch J.G(2018)[5]对完整岩石的标定过程，分别标定平板模型的法向与切向接触刚度比kˉ*，有效模量Eˉ*，黏结抗拉强度σˉc与黏结内聚力cˉ。遵循控制变量的原则，每组模拟试验改变一个微观参数的值，保持其他参数不变，取取值范围中间值。进行一系列的单轴压缩和拉伸模拟试验后得到了如图5所示的微观参数与宏观参数之间的关系。以灵敏度分析的结果为指导，在GUTIÉRREZ-Ch J.G 所提出的标定过程中加入对抗拉强度的校准，新的校准顺序遵循图4 所示的流程图。

图4 微观参数的分步迭代过程Fig.4 Iterative process of microscopic parameter

对于平行黏结模型参数的匹配，通常令模型的黏结抗拉强度与黏结内聚力相等，BAHAADDINI 等[4]用平行黏结颗粒模型标定Hawkesbury 砂岩的宏观力学参数[10]时，得到的颗粒模型抗拉强度远大于真实岩体的抗拉强度，本文通过考虑抗拉强度校正的参数匹配方法(图4)再次对平行黏结颗粒材料和平板黏结颗粒材料进行标定，其标定得到的颗粒黏结材料宏观属性见表1。

由表1中本文的标定结果可知，平行黏结模型依然不能同时满足抗拉强度与抗压强度的校正，这是因为抗拉强度校正完成后，平行黏结模型材料能达到的单轴抗压强度会产生一个最大限制，这个限制值远小于他所对应真实岩体的抗压强度，而平板模型材料不会存在这样的限制(见图6)。

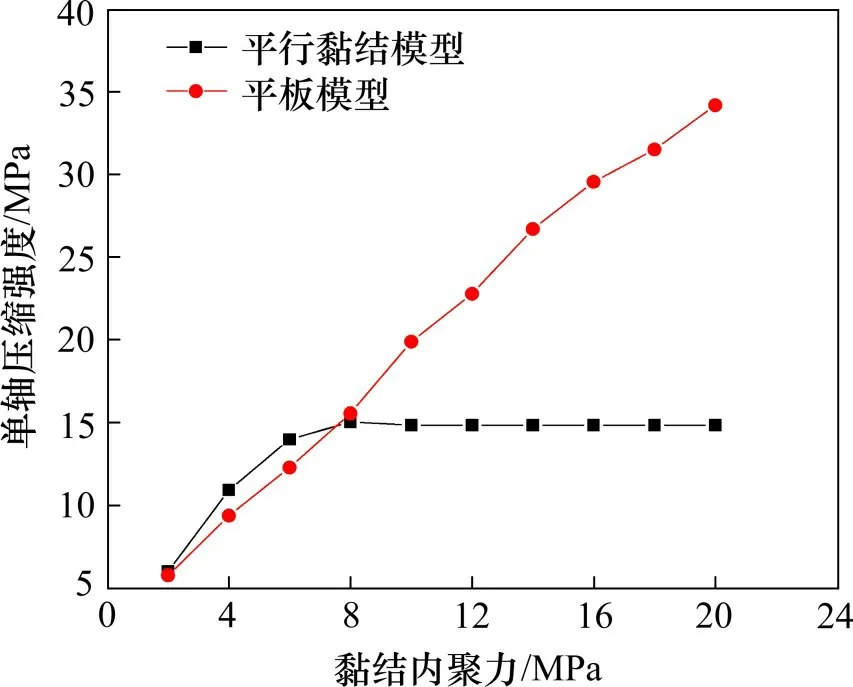
图6 接触模型内聚力对宏观单轴压缩强度的影响Fig.6 Effect of cohesion of contact model on uniaxial compressive strength of the macroscopic material

表1 平行黏结模型材料和平板模型材料的宏观属性Table 1 Macroscopic properties of parallel bond model materials and flat joint model materials

2.2 优化试验设计及数值试验结果

虽然上述的迭代匹配方法能够得到较为准确的平板模型参数匹配结果，但是匹配过程需要严格遵守迭代的顺序，只有在前一个参数校准成功后，才能进行下一个参数的校准。并且若要对其他不同类型的岩石进行标定，整个标定过程需要重新开始，这将是个十分耗时并且繁琐的工作。

目前试验设计方法(DOE)已被用于开发更有效的DEM 标定方法[12]。DOE 被定义为一种结构化的、有组织的方法，用于确定影响过程的因素与该过程的输出之间的关系[3]。故本文通过数理统计学中的试验设计，基于前文得到的微观参数与宏观参数之间的关系，针对多种岩石数值模拟研究中的微观参数标定问题进行进一步的探讨。现已有许多不同的DOE 方法，方法选择主要取决于分析的目的和要调查的因素的数量。Box-Behnken 设计试验法(BBD)可以对3～7 个因子进行检验，检验次数为15～62 次。当因子数目相同时所需的试验次数少于中心组合设计的试验次数，另外BBD法不存在轴向点，所以在设置因子水平范围时可避免出现负值[13]。故选择BBD 法简化参数标定过程，设计过程如下：首先选取单轴抗压强度USC，弹性模量E，泊松比PR和抗拉强度DTS作为试验指标。若不考虑颗粒自身属性和尺寸效应的影响，只考虑接触模型的变形与强度参数，选取黏结有效模量Eˉ(EC)，黏结刚度kˉn/kˉs(KK)，黏结抗拉强度σc(TS)，黏结内聚力cˉ(CS)4 个平板模型的主要微观参数作为试验因素。

最后计算试验因素范围，根据3.1 数值试验结果进行线性拟合：得到宏观弹性模量与EC的关系式：y=0.648x-0.006。根据目标标定对象宏观参数值，设计的岩石宏观抗拉强度范围为5～11 MPa。将y=2 和y=10 代入上式，得到x=7.79 和x=17.18，因此黏结抗拉强度TS 编码范围为7.5～17.5 MPa，同理，设计弹性模量范围取50～80 GPa，泊松比范围取0.15～0.3，单轴压缩强度范围取110～220 MPa，分别代入到图5 中宏观参数对应线性拟合公式，得到黏结刚度KK，黏结有效模量EC以及黏结内聚力CS的编码范围，具体取值范围以及编码公式见表2。

表2 微观参数及其标定范围Table 2 Microscopic parameters and calibration ranges

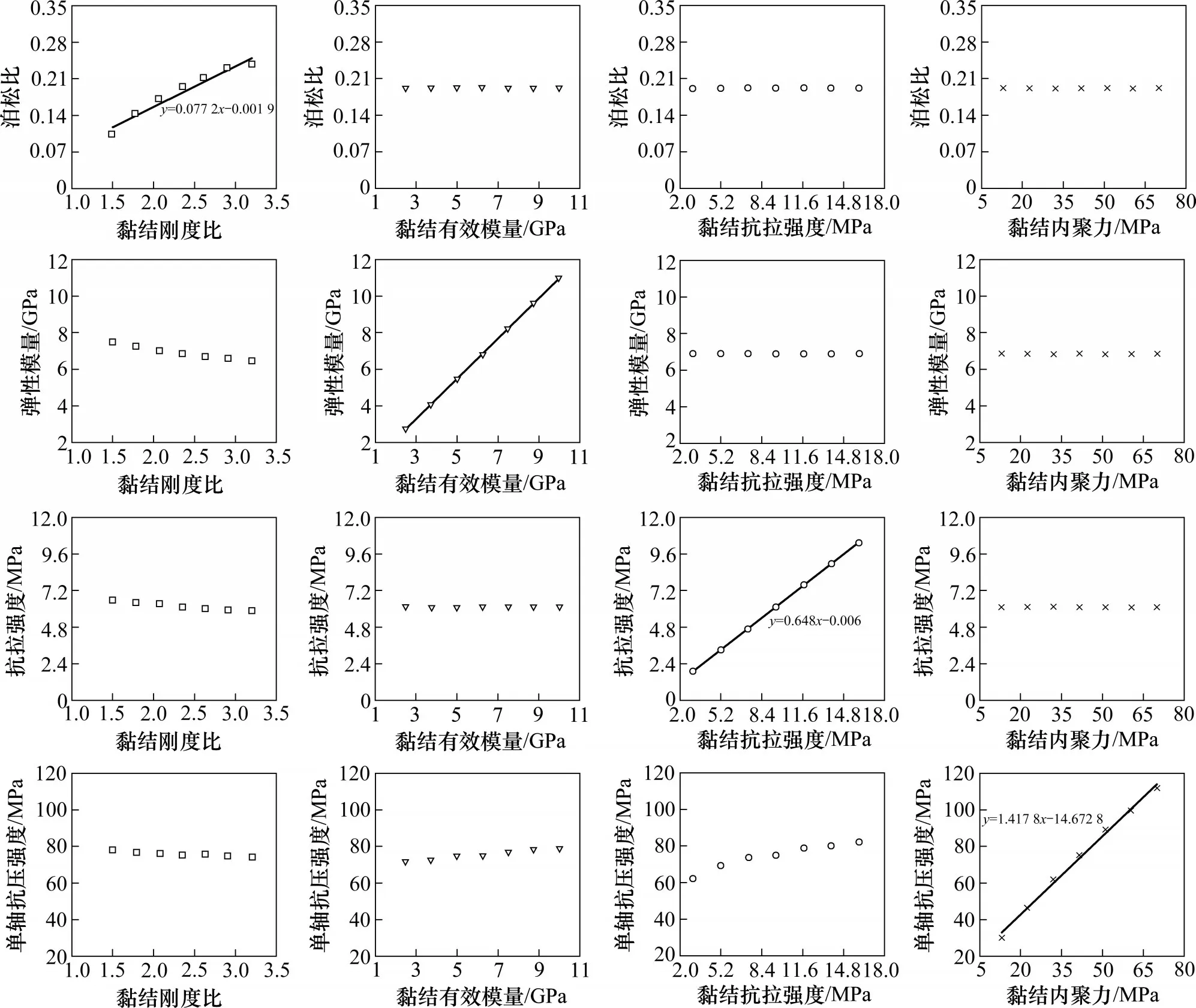
图5 平板模型的微观参数与模型宏观力学参数之间的敏感性分析Fig.5 Sensitivity analysis between the microscopic parameters of the flat joint model and the macro-mechanical parameters of the model

根据设计方案进行模拟试验，基于单轴压缩数值试验与直接拉伸数值试验的结果，计算得到每组数值试验的单轴抗压强度UCS，弹性模量E，泊松比PR和抗拉强度DTS，方案和计算结果见表3。

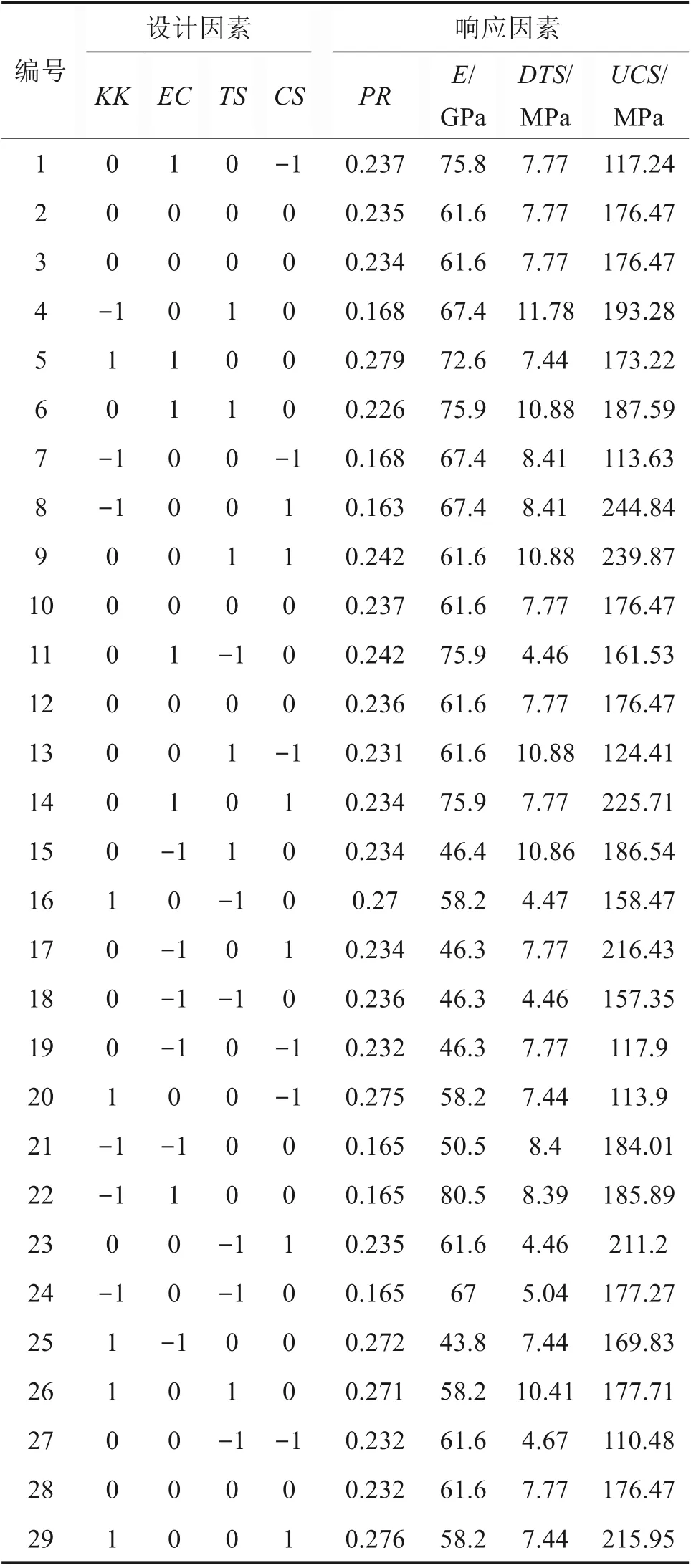
表3 BBD设计矩阵以及数值模拟结果Table 3 BBD design matrice and numerical simulation results

3 结果与讨论

3.1 统计分析

为简化求解，本文均采用如式(1)所示的线型模型，使用Design Expert 软件别对泊松比、杨氏模量、单轴抗压强度和抗拉强度4个宏观力学响应进行拟合分析，拟合结果见表4，R2与精密度等统计特征通常作为模型选择的依据。R2越接近1，说明模型拟合效果越好，并且要求精密度比率大于4，模型才是合理有效的。由拟合结果可知R2与精度均满足拟合条件，4 个宏观参数均可以采用线性模型来拟合。最后分别计算每个宏观参数对应微观参数的影响系数见表4。

表4 泊松比、弹性模量、抗拉强度和单轴压缩强度的BBD设计多元线性模型分析结果Table 4 Analysis results of multiple linear model of BBD design of poisson’s ratio,elastic modulus,tensile strength and uniaxial compressive strength

Y=I0+A×KK+B×EC+C×TS+D×CS(1)

式中：I0表示常量，A，B，C和D为方程系数。

3.2 求解方程

由分析结果得到4 个宏观因素与4 个微观因素之间的矩阵关系方程：

式中：

故由方程(2)的解X=A-1(Y-b)，化简得到黏结刚度比、有效模量、黏结抗拉强度、黏结内聚力的表达方程为：

3.3 方法验证

根据4种经典硬岩的物理试验结果进行微观参数的标定，代入前文提出的方程解析式(3)得到4种岩石的微观参数，如表5所示。

将表5 中的微观参数赋予到PFC2D 颗粒黏结模型中，得到单轴压缩和拉伸条件下数值模拟结果，与物理试验宏观参数的结果进行对比，见图7[8,14-16]，4 个指标的相对误差大部分都在5%左右。证明式(3)对同一尺寸模型的参数匹配具有通用性。

表5 平板模型黏结颗粒微观参数Table 5 Microscopic parameters of flat joint bonded model

图7 岩石宏观力学参数模拟值与试验值对比Fig.7 Comparison of numerical and experimental values of rock macro-mechanical parameters

4 结论

1) 颗粒黏结模型的宏观力学参数与接触模型微观参数存在一些对应影响关系，并且宏观力学参数随着主要影响因素的增大而增大。颗粒黏结材料的泊松比主要受黏结接刚度比影响，有效模量主要与黏结有效模量有关，抗拉强度的变化主要由黏结抗拉强度控制，单轴压缩强度受黏结内聚力影响的同时也受黏结抗拉强度的控制。

2) 通过分步迭代调整接触模型的黏结抗拉强度和黏结内聚力时，平行黏结模型材料的单轴抗压强度与抗拉强度之比只能达到一个较小的值，而平板模型材料能够与较高抗压拉强度比的岩体宏观响应相匹配。

3) 标定同一尺寸多种岩石的颗粒黏结模型参数时，可利用BBD试验设计方法建立岩石泊松比、弹性模量、抗拉强度和单轴压缩强度与接触模型微观参数黏结刚度比、有效模量、黏结抗拉强度和黏结内聚力之间的线性关系方程简化模拟参数匹配的步骤。