磁浮列车随机稳定性及首次穿越问题研究

黎燕霞，徐磊

(1. 中南大学土木工程学院，湖南长沙 410075；2. 高速铁路建造技术国家工程实验室，湖南长沙 410075)

磁浮列车由于具有冲击小、振动小、噪声低、能耗低、曲率大、爬坡陡等优点，受到越来越多的青睐[1]。目前，世界上关注的磁悬浮模式有德国TR 系列EMS 型常导电磁悬浮(10 mm，430 km/h)、日本MLX 系列EDS 电动型低温超导磁悬浮(100 mm，550 km/h)和中国HTS系列永磁型高温超导磁悬浮(10 mm，620 km/h)[2-3]。超导体具有完全抗磁性和磁通钉扎特性，形成悬浮高度和左右导向无需控制的自稳定系统[4]。由于明线上运行的常导吸力型高速磁悬浮列车本身的不稳定性与《高速磁浮交通车辆通用技术条件》(CJ/T 367—2011)中11.3条要求“在各种工况下，悬浮系统可以适应的最大起伏机械间隙不小于29 mm”需要相互平衡，磁浮列车稳定性问题应运而生[5]。磁浮间隙振幅超限使得磁浮列车运动轨迹可能偏离初始平衡中心，使得电磁铁的电磁环流过载饱和，导致失稳，影响舒适度。关于磁浮列车稳定性的研究工作往往关注磁浮系统控制器、自激振动、车轨参数匹配指标等，然而磁浮车自身是不稳定的，需要通过相关方法增强稳定性。LI等[6]对高温超导磁悬浮的相图、proportion integral derivative (PID)控制器进行了分析。高温超导磁悬浮的横向相图出现远离中心位置2 个不稳定的鞍点和1 个中心稳定位置稳定的焦点。PID 控制器设置有益磁浮车保持良好的运动稳定状态。王连春等[7]建立单悬浮点-弹性桥梁简化的耦合的模型，从能量传递的角度阐述了自激振动原理，从耦合系统的特征多项式的角度分析了自激振动机理。CHEN 等[8]建立车辆悬浮单元和柔性轨道梁的非线性耦合动力学模型，依据参数变化确定平稳性及其范围，表明车辆参数和轨道梁静态挠度之比的合理匹配指标有益车轨避免共振，维持稳定。此外，随机不平顺、气动荷载、磁浮车质量、磁浮架质量等随机激励荷载对磁浮列车稳定也有重要影响，时谨等[9]探讨了合理的磁浮线路功率谱形式，分析了导轨随机不平顺对系统动力学指标影响规律。SHEN[10]等测试了磁浮系统在不同导轨不平顺激励下的响应，认为其是导致系统振动的敏感因素之一。XU 等[11]认为单点的车-轨耦合模型在导轨不平顺激励作用下悬浮间隙频率和振幅增加。WU 等[12]计算了磁浮车轨耦合系统在风荷载的响应，认为气动荷载显著增大了磁浮车的加速度。WU 等[13]利用特征值分析，研究了气动荷载悬浮稳定性的影响，向上的空气动力荷载或俯仰力矩可能导致动态不稳定，向下的空气动力荷载可能导致静态不稳定。王党雄等[14]模拟了2 种质量在简支梁上通过和静悬浮时的车体、悬浮架、简支梁的振动加速度，试验表明，简支梁加速度在60 Hz处有较大峰值，这一频率(60 Hz)不受悬浮质量影响。悬浮质量越大，悬浮系统的不稳定性对车体和悬浮架加速度的影响较大。随机动力学与控制的哈密顿理论体系[15]、路径积分法[16]为研究非线性系统FPK方程的随机稳定提供了计算方法。尽管已有许多研究人员关注磁浮系统控制、自激振动、车轨参数匹配指标、导轨随机不平顺、气动荷载、悬浮质量等对稳定的影响，但从左边界特征值、首次穿越时间分析的研究尚不多见，在此，基于此分析方法对EMS 型磁浮列车稳定性及首次穿越时间开展研究。

1 磁浮列车动力学模型

一般来说，模型复杂性取决于其目的。倘若通过分析车辆振动响应来评估系统平顺性、舒适性、安全性，模型应该是完整的、准确的；而运动稳定性宜参考来自国防科大磁浮中心团队[7]认可的包含最核心要素的磁悬浮最小耦合模型，该模型具有更好的效率。

模型假设如下：

1) 根据运动稳定关键因素，以磁浮车、磁浮架[17]、悬挂件、导轨等为研究对象；

2) 忽略电磁铁错位布置、导轨转弯半径、导轨高差、导向等次要因素，使复杂的振动系统得以简化，提高求解效率；

3) 依据空气弹簧实验数据[18]设置非线性特征系数；

4) 将外部激励反演为近似一致白噪声激励[19-20]，磁浮力等效线性化[21]。

5) 磁浮架、磁浮车质量的波动近似为白噪声激励[14]。

磁浮车动力学模型及参数分别见图1和表1。

图1 磁浮车系统模型Fig.1 Maglev vehicle system model

磁浮系统微分方程如下：

式中：m1为磁浮架质量；m2为磁浮车质量；k1为磁浮架自振刚度；g为重力加速度；k2为磁浮车自振刚度；z0为磁铁初始位移；z1为磁浮架位移；z2为磁浮车位移；kcz为悬挂线性刚度；ccz为悬挂线性阻尼；ɑ1和ɑ2为非线性刚度系数；β为非线性阻尼系数；sgn为符号函数；δ为非线性阻尼耦合幂次；kδ为导轨随机不平顺系数；kv为气动荷载系数；fv(1/2ρAC3(V+U)2)为气动荷载；fm0为初始磁浮力；kep为等效磁动刚度；ked为等效磁动阻尼；ξ1为轨道不平顺激励；ξ2为风压激励；ξ3为磁浮架激励；ξ4为磁浮车激励。

导轨随机不平顺变量ξ1(t)，风压功率谱随机变量ξ2(t)，磁浮车激励ξ3和磁浮架激励ξ4。需满足以下关系：

2 磁浮列车随机稳定性求解

2.1 随机平均方法

基于随机平均方法的一维哈密顿Ito＾方程可预测随机稳定。通过该一维哈密顿Ito＾方程可以获得随机非线性方程临界稳定的表达式。

为便于计算，广义位移变量的转换如下：

式中：qi为广义位移；pi为广义动量，i=1～2。

式(1)经过降阶后的方程如下：

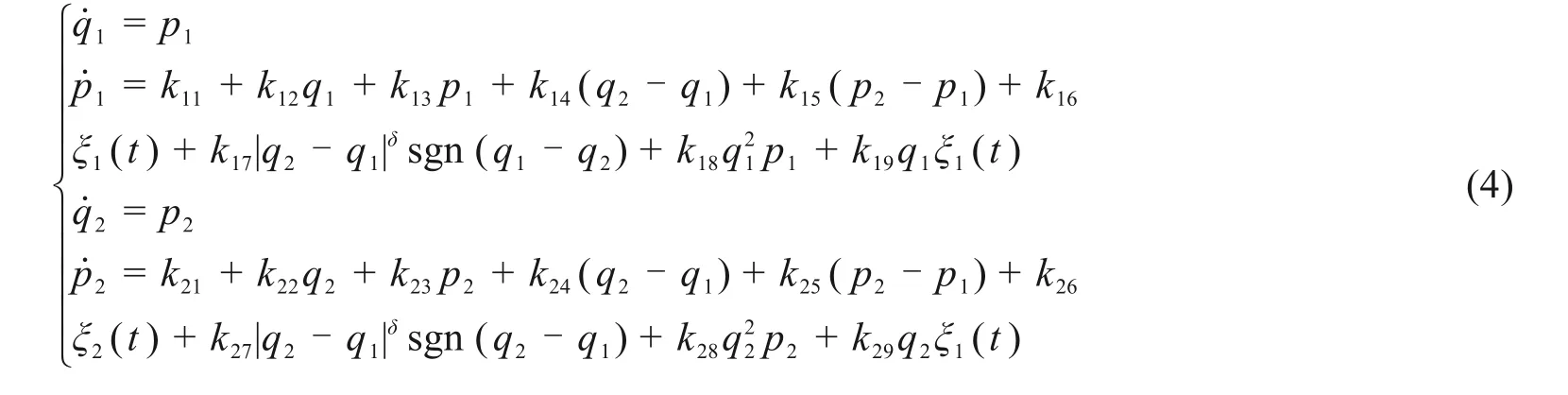
式中：

哈密顿能量方程为：

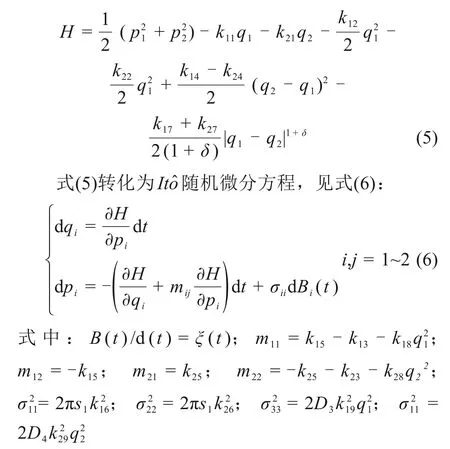
哈密顿系统涉及的变量均为独立变量，其方程从概率上收敛于一维的漂移和扩散过程。

Ito＾方程的平均哈密顿方程为

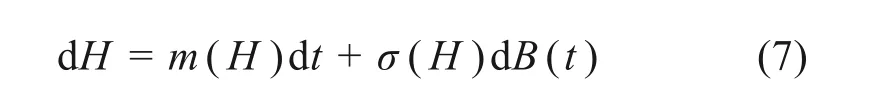
式中：m(H)为漂移系数；σ(H)为一维扩散过程；H(t)为扩散能量。

式(6)经空间平均后，代入式(5)，漂移系数和扩散系数积分表达式为式(8)：

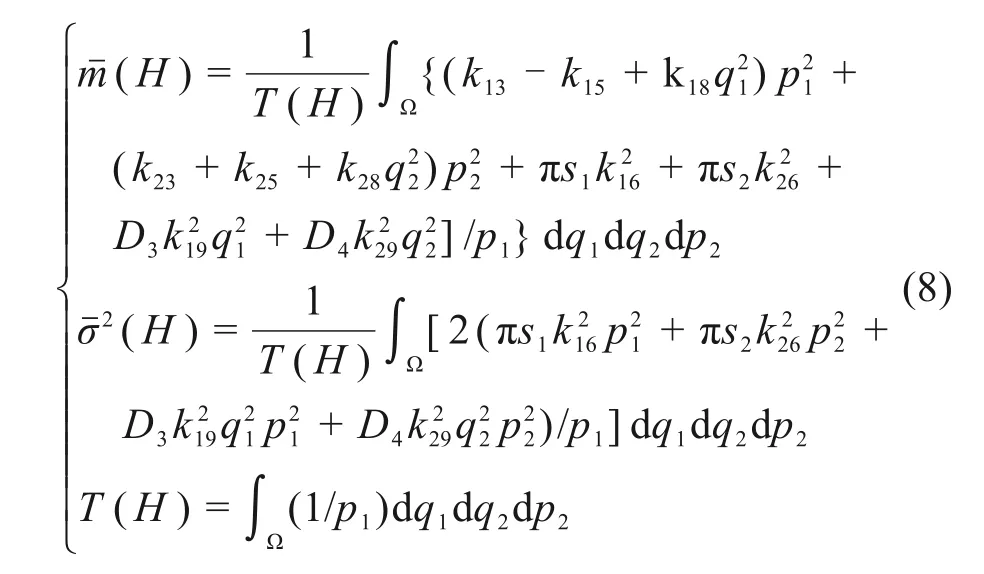
引入极坐标

2.2 磁浮列车左边界特征值求解

一维扩散过程的随机稳定性由该过程在边界上的形态体现。对拟不可积Hamilton 系统在等能量面上可作遍历假设，即H(q,p)=H为常数约束下，系统状态以等概率分布于等能量面上。时间平均可代之以空间平均，原有的多个动力学方程的边界条件，可代之以相应的1维Hamilton系统的边界条件。从而为边界类别判别稳定性方法的实施奠定了基础[19]。

当H→0，系统各重力、磁浮力、气动力会有一个调整后平衡，暂不考虑1阶。当H→0且δ>1，

忽略高阶，取2阶的近似值，式(5)转化为

那么，左边界扩散系数指数、左边界漂移系数指数、左边界特征指数，分别表达如式(13)。

考虑随机系统只要存在外激即失稳，分2类情况进行讨论。

1) 当S1≠0；S2≠0，漂移系数、扩散系数、特征指数如下：

此时为进入边界[19]，系统平凡概率不稳定，可考虑首次穿越问题。

2) 当S1=S2=0，漂移系数、扩散系数、特征指数如下：

根据第1类奇异边界类别的进一步分类依赖于特征值CL[19]，即：

2.3 磁浮列车首次穿越时间求解

条件可靠性函数R(t|H10,H20)满足下列后向Kolmogorov方程：

式中：mˉr，σˉrk由式(19)中mˉ1，σˉrk以H10与H20得到。

初始条件为R(0|H0)= 1，H0∈Ω。Гc上边界条件为R(0|H0)= 0，H0∈Гc。定性边界条件需利用方程(21)与mˉr，σˉrk在Г0上之值化为定量边界条件。它们是Г01上：

首次穿越时间的k阶条件矩，可从求解下列广义Pontryagin方程得到：

3 磁浮车随机稳定性分析

3.1 磁浮车左边界特征值分析

扩散过程在边界上的性态在很大程度上决定于整个磁浮车动力系统稳定的状态。哈密顿一维能量扩散过程的概率渐近稳定性完全由该过程在边界上的性态决定，详细参考文献[19]。依磁浮车-磁浮架边界分类分析，当系统处于稳定或失衡状态时，其相互关系见图2。

图2 磁浮车系统全局稳定性示意图Fig.2 Global stability of a maglev vehicle system

当CL=1 时，为系统临界稳定状态，经计算可得：

当特征指数小于1时，能量趋向稳定左边界(H→0)处，具有平稳解，此时系统是全局稳定的。当特征指数大于1 时，能量远离零点左边界(H→0)，能量在左边界(H→0)和右边界(H→∞)间徘徊，此时系统的稳定状态要根据其流动和扩散情况确定。从式(32)可以看出，当特征指数为1 时，是系统的临界状态。根据式(32)可导出系统各个参数约束关系，如图3～5。

图3 各参数变化的特征值Fig.3 Character values of left boundary vary with parameters

从图3可以看出，随着磁浮架质量激励D3和磁浮车质量激励D4增加，CL越大，越不利于稳定；随着等效磁动阻尼ked，随着悬挂线性阻尼ccz磁浮架质量m1，磁浮车质量增大m2，CL逐渐减小，越有益于稳定。随着磁磁浮车质量激励D4增加，磁浮车质量m2增加到一定的程度，再有变化，CL指标集中一点，基本保持不变，并小于3。

从图4 中可以看出，当CL指标为1，即临界状态时，可以导出两两参数之间的约束关系。ked-D3和Ccz-D3二维稳定域呈现递增趋势。

图4 二维稳定域Fig.4 Two-dimensional safe region

从图5 中可以看出，从式(3)可以导出任意2 个参数之间与特征值CL的关系，形成三维图。绿色水平层(CL=1)以上为由不稳定向失稳发展的方向。当ked/Ccz→0且D3→∞时，集中空间坐标右上角出现失稳报警区域；当m1/m2→∞且D4→∞时，集中空间坐标右上角出现箭头所示意失稳报警区域。

图5 三维稳定域Fig.5 Three-dimensional stable region

3.2 磁浮车首次穿越分析

根据2.3 的推导，上述方程可用有限差分法五点格式进行可靠度函数和首次跨越时间求解。

从图6中可以看出，外激S1≠0且S2≠0对相同的可靠度情况下，时间偏短。

图6 可靠性函数R(t)Fig.6 Reliability function

从图7中可以看出，外激S1≠0且S2≠0对相同能量情况下，时间偏短。

图7 平均首次穿越时间Fig.7 Average time of first-passage failure

4 结论

1) 基于哈密顿理论的随机平均方法，可以导出左边界特征值方程，以便进一步考虑随机激励对稳定性的影响，数值计算表明本文方法有效。

2) 相对于确定性特征值，等效动磁阻尼和悬挂线性阻尼越大，磁浮架和磁浮车质量及其参激强度越小，越有益于维持稳定。在临界稳定状态，各参数存在相互匹配关系。导轨随机不平顺激励且气动荷载激励不为0 时，系统平凡概率不稳定，在相同可靠度和能量情况下，首次穿越时间最短。

3)下一步可与平稳性、舒适度等指标相结合，共同优化参数范围。