数学表征：儿童数学学习的衔接性隐喻——以五下“圆”的大单元学习为例

潘香君

近年来，隐喻作为一种思维方式和认知现象在学校教学中受到广泛关注。在教学中，笔者发现，由于数学自身抽象的特点，有些学生难以理解数学知识，对数学学习的理解往往停留在浅表层，不擅长对单项知识点进行系统化建构，不能熟练地迁移运用方法。隐喻可以将数学中的抽象化为具体，将未知化为已知，助推学生认识和表达复杂的数学问题，并通过发展学生的多元表征能力，让他们在数学学习过程中建构体系化的知识，孕育数学思想，最终指向其思维的发展。

一、隐喻与数学表征的内涵解读

在狭义层面，隐喻是比喻的一种类型；在广义层面，隐喻是一种思维方式和认知现象，是人类认知和文化建构的基本方式。它是指利用熟悉的事物去构建对未知事物的理解，所以必然存在于教学实践中。

数学表征是数学学科的关键能力，既可以反映儿童数学学习的过程，又能呈现儿童数学学习的结果。它是指儿童利用已有的经验，借助熟悉的事物，去构建对未知事物理解的外显方式。数学表征可分为内在表征与外在表征，我们研究较多的是外在表征。外在表征是指需要学生理解和掌握的数学知识点等学习对象的外在形式。这种外在形式可以通过动作、图示、语言等方式外显学生的认知过程以及理解程度。动作表征、图式表征、语言表征等其实就是儿童在认知与理解等方面的隐喻方式。因此，可以将数学表征看作儿童数学学习的衔接性隐喻，它能在认知与思维之间架起一座桥梁，从而有助于儿童更好地建构认知与发展思维。

二、用好数学表征这个衔接性隐喻的策略

在数学教学中，教师要注重引导学生在学习中发展表征能力，用好这个衔接性隐喻。下面，笔者以苏教版五下“圆”的大单元学习为例，谈一谈怎样来引导学生建构深度表征，有效实现数学表征的衔接性隐喻的作用。

教学前，笔者尝试进行大单元设计（如表1），给学生搭建多元表征的平台，建构各种信息的联合体，编织知识、方法的结构网络，以期促进学生积累丰富的活动经验，联通内外表征，让其思维过程看得见。

表1 “圆”的大单元设计

（一）在前学中形成结构化表征

所有的学习都是基于原有经验的迁移。在学习“圆”这一单元之前，教师先组织学生回忆已认识的平面图形，以三个问题激发他们回顾反思：在认识这些平面图形的过程中，我们研究了它们的哪些特征？是怎样开展研究的？如果继续研究平面图形“圆”，你会研究它的哪些特征？怎样研究呢？请你用自己喜欢的方式整理相关内容。大部分学生借助思维导图整理已学知识、方法，教师在图示表征中解读到了学生内在结构化、模型化、深层化的思考。

1.结构化：从点状走向块状。

从学生的思维导图中，教师看出他们已经能抓取每一课时的重点内容。于是，引导学生通过整理与交流，提炼研究平面图形的基本点，即聚焦边、角的特征开展研究，并探索平面图形的周长与面积。学生在核心问题引领下展开思考，勾勒结构化的知识图。

2.模型化：从经验走向结构。

数学中的模型思想是建立在学生体会和真正理解数学的基础上的，这在学生的思维导图中可以看出来。学生在其中获得了对平面图形的研究经验，从而推想在学习圆的知识时也可以研究这些内容：什么是圆？怎样画圆？圆的面积怎么算？由此及彼，学生的学习逐渐从经验走向结构，主动创造丰富的学习过程。

（二）在合学中体验多元化表征

1.动作表征：孕育概念理解。

动作表征是以实际动作再现知识经验，用自己的身体来影响周围世界的一种方式。在“你能想办法画出一个圆吗？”这一活动中，有的学生借助透明胶带、学具篮里的硬币或圆片描画圆，有的自制工具画圆，更多学生选择直接使用圆规画圆。在经历不同方法画圆到学会用圆规画圆的过程中，学生能够初步感知圆是怎样的图形。学生虽然不能直接抽象定义圆，但能体会到定点就是圆心，定长就是半径，圆是封闭的曲线，为其后续学习奠定了基础。在画圆过程中，学生还能发现圆的一些特征：有无数条半径，而且同一个圆中的半径都相等，圆心决定圆的位置，半径决定圆的大小……深入理解了圆的特征。

2.图形表征：探寻公式关联。

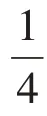
（图1）

（三）在创学中建立关联性表征

在教学中，教师要注意启发学生运用已经习得的经验去开启新的认知。练习中有这样一道生活情境题：一块草坪上的喷水装置最远射程是12米，这个喷水装置最多能喷射多少平方米？此题中的喷水装置就是现实生活中草坪、花圃的灌溉系统，学生结合图片观察能理解“射程”是圆的半径，喷出水的范围形成了圆的面积。教学时，教师不能就此戛然而止，而应该趁热打铁，出示变式题：如果让你来改编这一题，你还会怎样改编呢？静静思考后，学生思维的火花开始绽放，有学生提出：公园里音乐喷泉的最远射程是10米，它最多能喷射多少平方米？降落伞的绳最长的是8米，它打开后的面积最大是多少？聚焦本质特征，关联生活情境，助推学生深度学习，不仅应注重从知识到知识的延续，还应学会从生活中抽象出数学问题进行解决。

（四）在拓学中深化多重性表征

1.微主题探究：多元表征外显发散思维。

学完“圆”后，教师鼓励学生找找生活中的圆，如牛奶瓶口（底）的面、小区里的圆形花坛、纽扣的面等，并引导他们灵活运用数学知识解决生活中圆的实际问题。怎样才能求出牛奶瓶盖面的周长和面积呢？首先需要想办法测量出它的半径或直径，借助两把三角尺和直尺可以测量出直径，然后可以通过计算分别求出周长和面积。学生思考后还总结出像这样比较小的圆面可以用尺量法解决，比较大的圆还可以用不同的方法解决。

2.大主题深探：多元表征彰显聚合思维。

为什么生活中许多物体的面要设计成圆形呢？学生利用各种资源开展“车轮为什么是圆的”主题探究。学生通过前期搜集资料、互动讨论，聚焦“车轮为什么是圆的”这一核心主题，确定研究的小课题，设计富有挑战性的任务。在研究过程中，有的小组动手制作各种形状的车轮模型模拟运动，在对比中感受圆形车轮的优势；有的小组到数学场馆中，对方轮车进行测量、分析、比较，并形成文字报告。各小组通过不同的研究方式，借助动作表征、模型表征、文字表征等呈现研究过程与结果。最后，在集体交流时，小组间的多元评价促进了学生言语表征能力的发展。

综上所述，在“圆”的大单元学习中，通过前学、合学、创学、拓学等多样化的学习活动，借助多元表征，学生逐渐明晰了圆的概念本质，并能活用知识解决问题。当儿童的数学表征逐渐走向深度，对于数学内容的理解能够进行多元化展示，表征这一隐喻架构起认知与思维的桥梁的作用也就很好地实现了。