基于学生立场的数学教材横向比较与教学建议

刘兆伟

摘 要 基于学生立场，从情境创设、活动设计、文化渗透这三个方面，对人教版、苏教版、北师大版和青岛版教材中“三角形的面积”内容进行横向比较分析，进而提出教学建议：情境创设从单元整体出发、活动设计从已有经验出发、文化渗透从意义理解出发。

关键词 学生立场 教材横向比较 三角形的面积 情境创设 活动设计 文化渗透

《义务教育数学课程标准（2011年版）》（以下简称《课标》）指出：“数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构，是实现课程目标、实施数学教学的重要资源。”虽然不同版本教材的设计理念、编排体系与逻辑结构等不完全一样，但它们都是依据《课标》编成的，教师在设计教学时，可通过对不同版本教材中的同一内容进行横向比较分析，丰富对所教内容的认识和理解，从而设计出更有利于学生发展的学习活动。本文以“三角形的面积”一课为例，对人教版、苏教版、北师大版和青岛版教材进行横向比较分析，并在分析的基础上提出教学建议。

一、教材分析

1.对情境创设的对比分析

《课标》指出：“教材所选用的学习素材应尽量与学生的生活现实、数学现实、其他学科现实相联系，应有利于加深学生对所要学习内容的数学理解。”人教版、北师大版和青岛版教材都选用生活素材创设现实情境，以引发学生的学习兴趣。人教版教材以红领巾为学习素材，并直接提出问题：“怎样算出红领巾的面积呢？”北师大版教材以流动红旗为学习素材，并直接提出问题：“如何求出这面彩旗的面积？”青岛版教材中则以道路标志牌为学习素材，并用“你能提出什么问题？”引导学生提出问题：“制作这个标志牌需要多少平方分米的铝皮？”

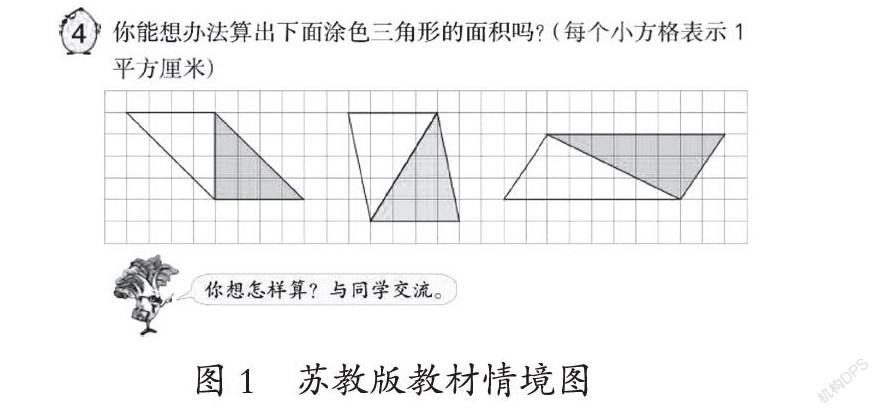
与上述三种版本教材不同的是，苏教版教材选择数学素材创设了纯数学情境：将三种不同类型的三角形置于方格图上的平行四边形中，让学生“想办法算出下面涂色三角形的面积”（如图1）。纯数学情境注重的是数学知识间的内在联系，学生在这样的情境中不仅能借助方格图数出三角形的面积，而且能依据三角形与平行四边形之间的联系算出三角形的面积，为学生探寻三角形的面积公式作铺垫。

2.对活动设计的对比分析

《课标》指出：“教材应设计必要的数学活动，让学生通过观察、实验、猜测、推理、交流、反思等，感悟知识的形成和应用。”人教版、苏教版和青岛版教材中探究活动的设计思路大致相同，都将三角形分成三类分别进行研究，最后归纳得到三角形的面积公式，这体现了分类和归纳的思想，但它们的侧重点不一样。

人教版教材设计的探究活动分三步进行。在提出探究问题后，启发学生“能不能将三角形也转化成学过的……”接着，引导学生用两个完全一样的三角形去拼平行四边形，并得出结论“用两个同样的三角形可以拼出一个……”最后，依据转化的过程推导出三角形的面积公式。苏教版教材设计的探究活动侧重下引导学生自主推导三角形的面积公式。在学生完成用两个完全一样的三角形拼平行四边形的活动后，组织学生讨论：（1）拼成平行四边形的两个三角形有什么关系？（2）拼成的平行四边形的底和高与三角形的底和高有什么关系？每个三角形的面积与拼成的平行四边形的面积呢？（3）根据平行四边形的面积公式，怎样求三角形的面积？通过这三个问题引导学生自主推导出三角形的面积公式。青岛版教材中设计的探究活动侧重于引导学生用数学的方式表达和思考，花了大量的篇幅用数学的方法分别演示将锐角三角形、直角三角形、钝角三角形加倍转化成平行四邊形的过程，并详细地描述了由平行四边形的面积公式推导出三角形的面积公式的推理过程。

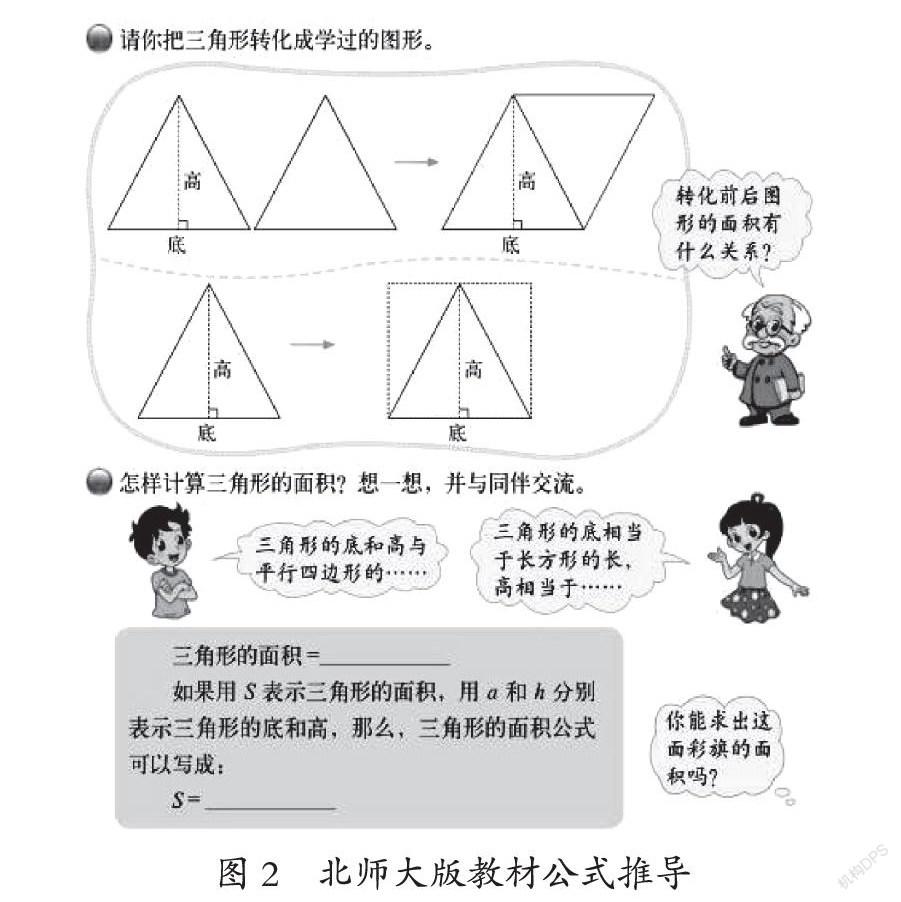
与上述三种版本教材不同的是，北师大版教材在提出探究问题后，直接将情境中的三角形抽象为一般三角形，并通过加倍法将这个三角形转化成平行四边形和长方形，再依据平行四边形和长方形的面积公式推导出三角形的面积公式（如图2）。

四种版本教材中，北师大版教材设计的探究活动最为开放，最具有挑战性，学生学习起来思维难度也较大，其他三种版本教材设计的探究活动则比较细腻，给学生提供了具体的方法引领。另外，人教版、苏教版和青岛版教材都将三角形加倍转化成平行四边形，而北师大版教材除了将三角形加倍转化成平行四边形外，还将三角形加倍转化成长方形。

3.对文化渗透的对比分析

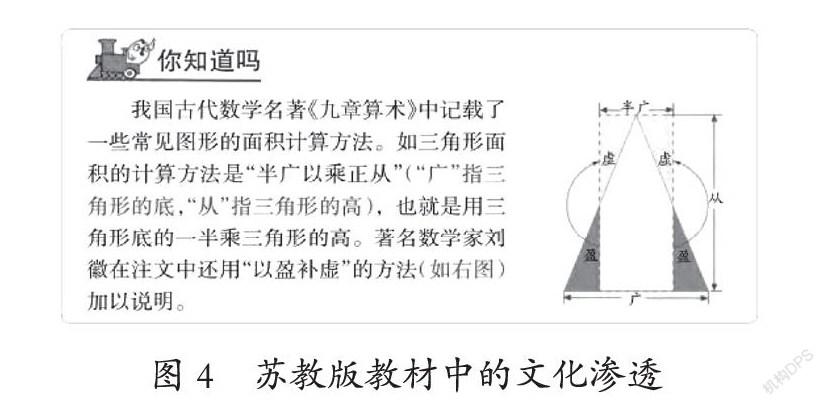
《课标》指出：“数学文化作为教材的组成部分，应渗透在整套教材中。”四种版教材中，人教版和苏教版教材都注重数学文化的渗透，而北师大版和青岛版教材对数学文化都未涉及。人教版教材在“你知道吗”栏目中，向学生介绍了《九章算术》中的长方形和三角形的面积计算方法（如图3）。苏教版教材中，不仅向学生介绍《九章算术》中的三角形的面积计算方法，而且配以刘徽所著《九章注解》中“以盈补虚”的图形，帮助学生理解“半广以乘正从”的意思（如图4）。

二、教学建议

1.情境创设从单元整体出发

数学知识具有整体性和结构性，每个知识点都处于一个相对稳定的系统之中。学生在数学学习过程中，不仅要掌握数学知识，而且要形成相应的认知结构。四种版本教材中“三角形的面积”的学习内容编排相似，这样的安排虽然也能帮助学生形成认知结构，但如果从单元整体教学出发创设情境，将更有利于学生从整体上把握本单元的学习内容，形成整体认知。

比如，在教学本单元的起始课时可以创设这样的情境：出示校园中一些区域的平面图，其中有长方形、正方形、平行四边形、三角形和梯形（甚至有组合图形），让学生分别求某些区域的面积。学生依据已有经验自然会用公式求得长方形、正方形的面积。在求得这两个图形的面积后，教师顺势引导学生回顾得到这两个面积公式的过程。随后，再让学生逐一思考怎样求平行四边形、三角形和梯形的面积，进行分课时教学。在分课时教学时，将此情境贯穿始终，后一课时在前一课时的基础上进行。这样就将“三角形的面积”置于“多边形的面积”这个整体中，学生在学习“三角形的面积”时，既承接前面学习中获得的知识经验和思维经验，又为后续学习梯形的面积积累新的经验，在学习的过程中逐步形成良好的认知结构。

2.活动设计从已有经验出发

学生学习的过程是经验不断积累的过程，新知的学习应建立在学生已有经验的基础上，这样才能被学生深刻理解和掌握，并能在学习过程中催生新的经验。因此，数学活动的设计应从学生的已有经验出发。

在学习本课之前，学生在多边形的面积计算方面已经具有的经验是：通过铺面积单位得到长方形和正方形的面积公式，以及将平行四边形等积转化成长方形得到平行四边形的面积公式。这些经验理应成为学生学习本课的基础，但四种版本教材中，并没有考虑学生的已有经验。苏教版教材中的例4直接暗示学生，两个完全一样的三角形可以拼成一个平行四边形，而没有给学生提供调用已有经验的机会。其他三种版本教材虽然都提出了类似于“能把三角形转化成学过的图形吗？”这样的问题以激活学生的已有经验，但学生依据已有经验，能够想到的是将三角形等积转化成长方形或平行四边形，而教材随后设计的探究活动中却是让学生将三角形加倍转化成平行四边形或长方形，与学生的已有经验脱钩。

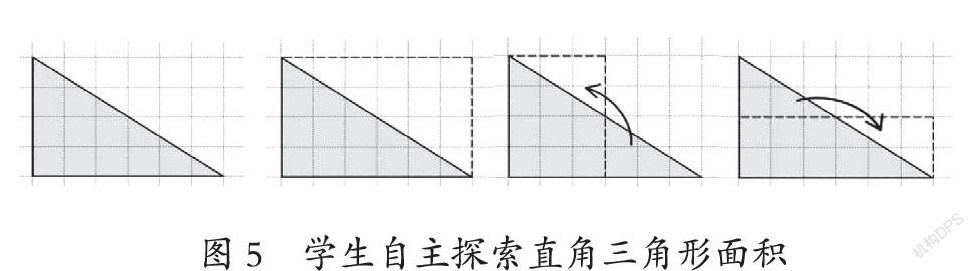
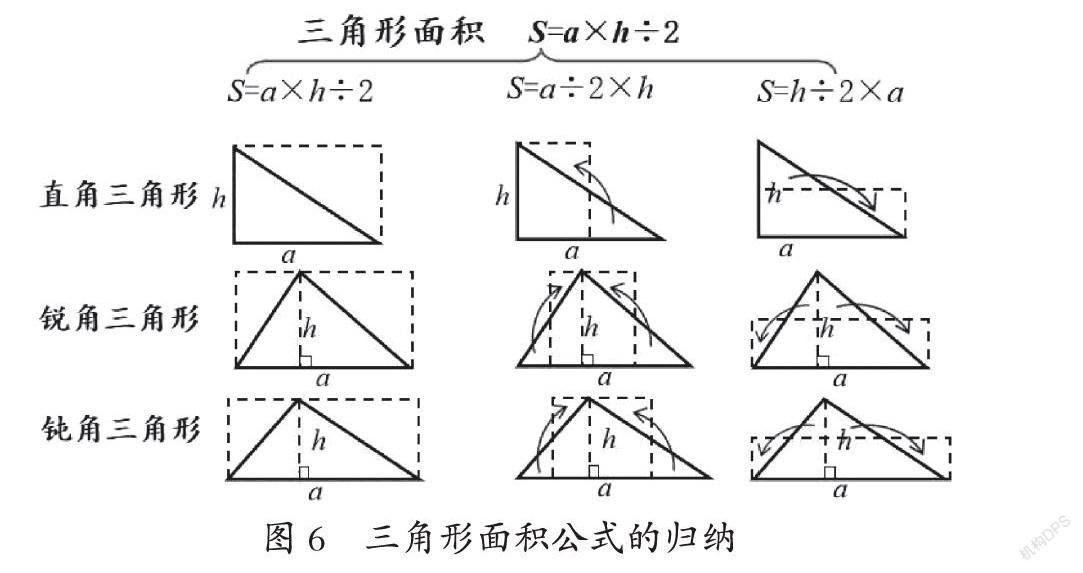
等积转化虽然是学生的已有经验，但用其来探寻三角形的面积公式思维难度较大，加上受课堂时间所限，所以四种版本教材都选择了直接让学生用加倍转化这一相对简单的方法探寻三角形的面积公式。其实，如果从关照学生的已有经验、发展学生的思维能力，以及积累活动经验的角度来看，完全可以让学生依据已有经验，自主探索三角形的面积公式。先让学生求一个方格图中的直角三角形的面积，学生除了能够数出这个三角形的面积外，还会想到三种方法将这个三角形等积转化成长方形，并算出面积（如图5）。接着，学生可以利用前面活动中获得的经验，将一般直角三角形等积转化成长方形，并得到直角三角形的面积计算方法，再依据直角三角形的面积计算方法类推锐角三角形和钝角三角形的面积计算方法。根据“所有锐角三角形和钝角三角形都可以沿高分成两个直角三角形”，运用直角三角形的转化方法将锐角三角形和钝角三角形等积转化成长方形，从而確定它们的面积计算方法。最后通过完全归纳得到三角形的面积公式（如图6）。这样从学生已有经验出发设计的探究活动，相比四种版本教材中设计的探究活动需要更多的时间，但相对于学生的学习体验与收获来说是值得的。

3.文化渗透从意义理解出发

数学文化凝聚了古人的智慧与创造，在数学课中渗透数学文化能够提升学生的素养，增长学生的智慧。虽然人教版和苏教版教材都注重渗透数学文化，但它们所采用的方式是附加式，即在课的最后通过“你知道吗”栏目向学生介绍《九章算术》中三角形的面积计算方法。但《九章算术》中三角形的面积计算方法是依据等积转化得到的，与教材中的加倍转化不一样，学生对其只是了解，感悟是不深刻的，所以他们很难从中感受到古人发现的伟大，更谈不上汲取智慧。

如果引导学生将探究三角形的面积公式的过程与古人发现三角形面积计算方法的过程结合起来，在经历了上述探究过程后，再出示“你知道吗”中的相关内容，学生不仅能够理解《九章算术》中记载的三角形面积计算方法，而且能体会“以盈补虚”的价值，并将其用于梯形面积公式的探究过程中。学生不仅从中获得数学知识，而且能够感悟到古人的智慧与创造，获得智慧的生长。

从学生立场出发，对多种版本教材中的同一内容进行横向比较，能够让我们突破自身的经验及思维定势，发现更多的教学可能，从而为学生的学习提供更好的教学设计。

[责任编辑：陈国庆]