渗碳12CrNi3合金钢疲劳寿命预测及变应力水平下残余寿命可靠性研究*

郭 扬 邓海龙③ 刘 兵 于 欢③ 郭玉鹏

(①内蒙古工业大学机械工程学院，内蒙古 呼和浩特010051；②内蒙古工业大学材料科学及工程学院，内蒙古 呼和浩特010051；③内蒙古自治区先进制造技术重点实验室，内蒙古 呼和浩特010051)

随着现代工业的发展，零部件向轻量化-高可靠性方向发展，多数零件受到循环加载载荷影响，且实际加载次数远远大于107周次[1-3]。为了确保零部件在使用寿命内不会发生过早的疲劳破坏，需要对零部件进行疲劳寿命预测及先验寿命下疲劳残余寿命评估。

机械零件的疲劳失效通常是由表面缺陷/内部夹杂物诱发的，在形成初始裂纹后经过很少的循环次数就导致零件的疲劳断裂[4]，因此一些研究人员提出[5-6]可以从裂纹扩展的角度来评估零件的疲劳寿命。邓海龙等[7]提出了以细晶粒区作为小裂纹与长裂纹扩展行为的转换点时的小裂纹+长裂纹扩展疲劳寿命预测模型。李伟等[8]在考虑了门槛强度因子的基础上分别提出了针对内部/表面失效的裂纹扩展寿命模型。吕绪明[9]等验证了两参数模型能够合理地预测恒幅载荷下的裂纹扩展行为。Bang D J[10]等建立了基于双参数驱动力和裂纹扩展阈值的长短裂纹扩展模型。

在工作载荷作用下，零件会由于局部应力集中而产生初始微裂纹，随着微裂纹的扩展，零件的损伤不断增加，残余寿命不断减小，发生疲劳失效的概率不断上升。吕海波等[11]提出了一种元件疲劳可靠性的剩余强度模型，以剩余强度R与载荷S作为参量，分析了结构元件的疲劳可靠性。谢里阳等[12]提出了基于载荷循环数-疲劳寿命的干涉模型，建立了不同载荷历史下剩余寿命分布参数变化的疲劳可靠性计算方法。凌丹[13]等提出了一种基于威布尔分布的疲劳剩余寿命可靠性预测方法，针对同一应力水平下的试样对疲劳剩余寿命进行了评估。然而上述方法未考虑到同一应力水平下数据点较少或处于多应力水平等情况。因此本文提出了一种变应力水平下疲劳残余寿命可靠性方法。

本文基于渗碳12CrNi3合金钢疲劳试验，研究其应力-寿命特性。通过疲劳试样断口观测，确定了失效机理及裂纹尺寸特征。从裂纹扩展角度建立了内部疲劳失效的疲劳寿命预测模型；最后基于不同应力水平下疲劳寿命威布尔分布特性，建立了残余疲劳寿命的可靠度模型及概率密度模型。

1 疲劳试验

1.1 试样及热处理

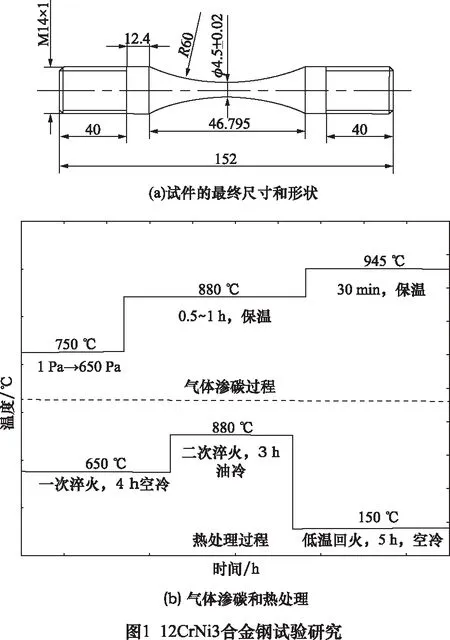
本试验研究材料为12CrNi3合金钢，其化学成分如表1所示。将直径为16 mm退火钢棒加工到沙漏状，再利用360 #～2000 #金刚砂纸沿试样轴向方向由低粒度至高粒度研磨试样表面，最终试样尺寸如图1a所示。为满足性能要求，对试样进行气体渗碳和热处理。使用井式气体渗碳炉，对试样进行气体渗碳，首先将渗碳炉升温至750 ℃，通入乙炔气体并保持炉内压强为1 Pa；其次将试样间隔5 mm放入渗碳炉中，将炉内压强增至650 Pa；之后将渗碳炉加热至880 ℃并保持0.5～1 h，使试件均匀受热；最后将渗碳炉加热至945 ℃并保温30 min。完成渗碳后，试样进行热处理，包括两次淬火和一次低温回火，如图1b所示。

表1 12CrNi3合金钢的化学成分 (wt.%)

1.2 微观力学性能

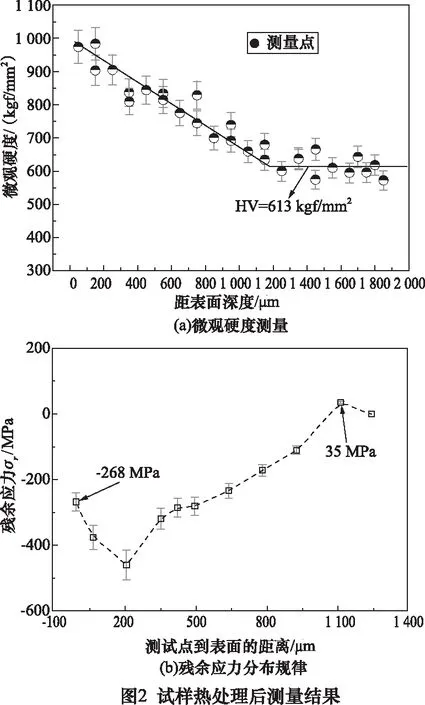
试样热处理后，截取中间漏斗部位一段镶嵌成金相试样，结合纳米压痕硬度测量仪，从试样表面到心部每间隔100 μm打点并测量维氏硬度(HV)，其误差棒为5%，结果如图2a所示。随着距离表面深度的增加，维氏硬度值呈现线性减小趋势，当距离表面约为1 200 μm时，维氏硬度值趋于平稳。这是因为随着距离表面深度增加，渗碳工艺的影响会越来越小。通过测量可知表面渗碳层维氏硬度最大值约为990 kgf/mm2，心部的维氏硬度均值为613 kgf/mm2且渗碳层深度约为1 200 μm。

基于TEC 4000 X射线衍射系统，获得残余应力分布规律，其误差棒为10%，结果如图2b所示。由图可知:表面残余应力为-268 MPa，且残余应力随着深度变化的趋势为先减小后增大，在达到正应力值再减小至零。这是由于为了使试样径向内的应力保持平衡，在渗碳层过渡区域，渗碳层与心部基体内的残余应力状态应互为反作用力。当测量点距离表面深度接近1 100 μm时，最大残余拉应力约为35 MPa。

1.3 疲劳试验方法

本试验使用高频疲劳试验机，用脉冲拉伸力(应力比R= -1)测试12CrNi3渗碳钢。试样分别施加不同的应力水平，破坏准则定义为断裂时的寿命。试验完成后，通过扫描电子显微镜观察所有的断口表面，确定断裂方式以及裂纹成核位置，同时观察裂纹的特定形貌特征。

2 结果与讨论

2.1 应力-寿命曲线

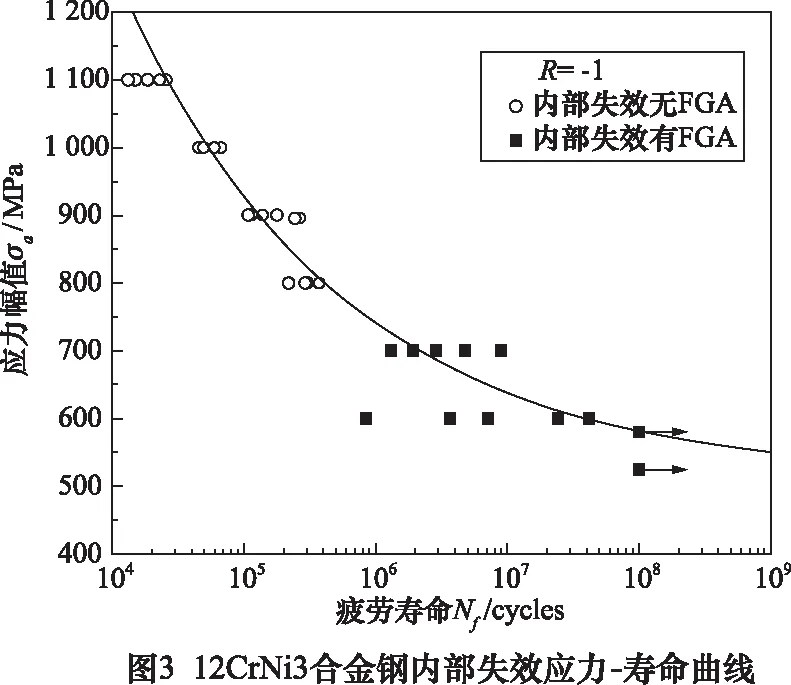
疲劳试验所得的应力-寿命数据点如图3所示。通过观察数据点可以发现应力和疲劳寿命具有负相关趋势，且不存在传统的疲劳极限。基于数据点的分布规律，得到应力-寿命拟合曲线如图3实线所示。

2.2 试样断口观察及失效机理分析

通过电子扫描镜观察12CrNi3试样的断口形貌，其典型断口形貌如图4所示。对于12CrNi3合金钢在R= -1时的内部失效，首先将断口区域划分为基体区和渗碳层。由于渗碳层的强化效果，裂纹均生成于内部基体区域，如图4a所示。在基体区可以观察到裂纹处的鱼眼特征，放大后如图4b及4d所示。鱼眼的外观看起来比较暗，这可能与裂纹扩展速率以及基体区域微观组织的差异有关。当应力幅值在700 MPa以上时夹杂物周围只存在鱼眼，由文献[14-15]可知，试样90%的疲劳寿命用于鱼眼的形成过程中。这就意味着，形成夹杂之外鱼眼之内的疲劳寿命可以看作是试样疲劳全寿命。而当施加应力幅值在700 MPa及以下时，鱼眼中心的夹杂物周围可以观察到一个明亮且粗糙的粒状区域，这个区域叫做FGA,此时可认为形成夹杂之外FGA之内的疲劳寿命可当作试样的全疲劳寿命,如图4c及4e所示。

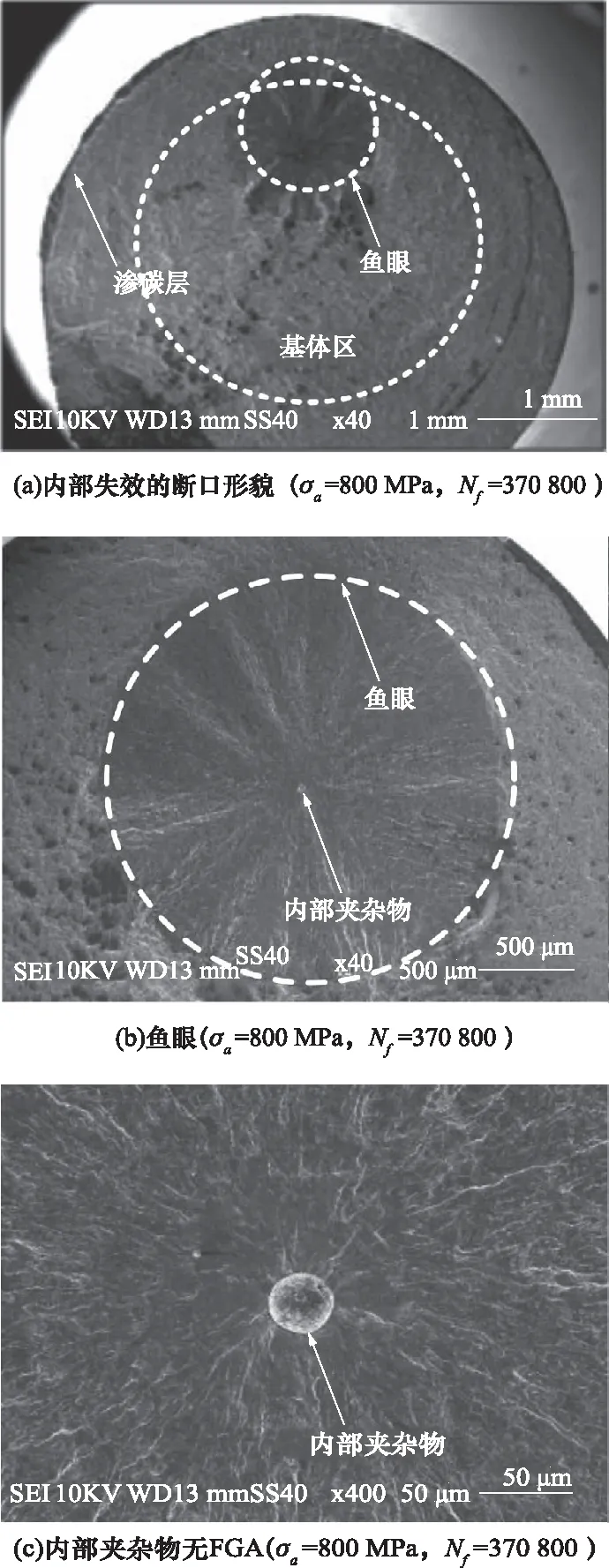
基于断口观察，发现所有试样的裂纹源均来自内部的非金属夹杂物，因此可认为渗碳12CrNi3合金钢的内部失效是由非金属夹杂物诱发的。在进行试验时，夹杂物周围会形成应力集中效应，进而形成微裂纹。随着加载时间的增加裂纹逐渐形成，最终导致试样断裂。

2.3 疲劳裂纹尺寸特征

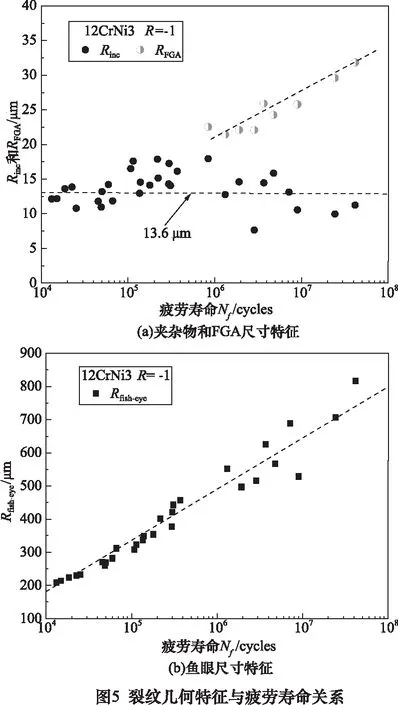
将Rinc、RFGA及Rfish-eye分别定义为夹杂物、细晶粒区及鱼眼区域面积的半径。基于扫描电子显微镜观测及图形处理软件测量，渗碳12CrNi3合金钢在应力比R=-1下，裂纹几何特征与疲劳寿命关系如图5所示。如图5a所示，Rinc介于7.6～17.6 μm，其均值约为13.6 μm，且与疲劳寿命及应力比无关；RFGA随着疲劳寿命Nf的增加呈增长趋势。如图5b所示，随着疲劳寿命的增加，Rfish-eye同样呈增长趋势。

2.4 等效应力强度因子

基于Murakami，Marines等学者的研究[16-17]，在恒幅载荷下，可将内部夹杂物，FGA及鱼眼等效为内部圆形裂纹，其等效强度因子可由式(1)给出：

(1)

其中：Δσ为施加应力的范围，在恒幅载荷下压应力对裂纹扩展的影响很小，因此可以用最大应力代替Δσ；Rinc，FGA，fish-eye分别为夹杂物，FGA和鱼眼的半径。

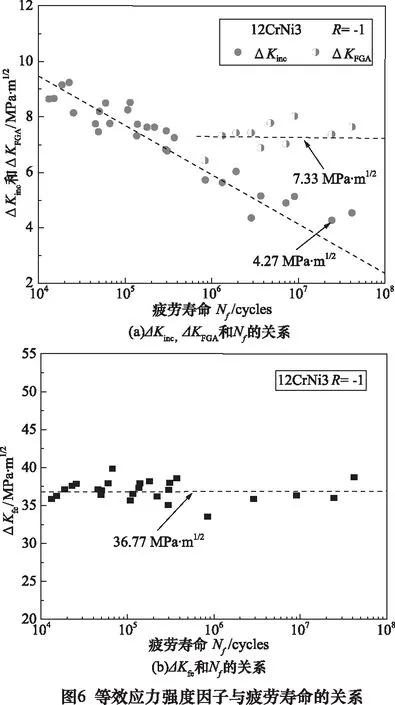
由等式(1)，可得到夹杂物，FGA和鱼眼的等效应力强度因子ΔKinc，ΔKFGA及ΔKfe与疲劳寿命Nf的关系，如图6所示。由图6a可知，随着等效疲劳寿命的增加，ΔKinc与Nf呈负相关趋势，其最小值为4.27 MPa·m1/2；而ΔKFGA趋近于固定值7.33 MPa·m1/2。由图6b可知，ΔKfe也趋近于固定值36.77 MPa·m1/2。

3 疲劳寿命预测模型

基于Erdogan和Paris[17]制定的Paris法则，裂纹扩展寿命预测模型如下所示。

(2)

式中：a为裂纹长度，N为疲劳寿命，ΔK为等效强度因子，C和m分别为疲劳裂纹扩展阶段的不相关于材料的裂纹扩展速率的系数及指数。

在Paris法则的基础上，结合Klesnil及Lukas[18]的研究，考虑到裂纹扩展阈值及其影响，进一步得到裂纹扩展速率式(3)。

(3)

其中：ΔKth为裂纹扩展阈值。

结合维氏硬度和裂纹尺寸特征，Murakami提出的一个通用方程来计算[18]裂纹扩展阈值，如式(4)所示。

(4)

其中：HV为微观硬度，取心部均值613 kgf/mm2。

对于内部疲劳失效无FGA形成，结合式(2)～(4)，由夹杂尺寸到鱼眼尺寸进行积分，可得：

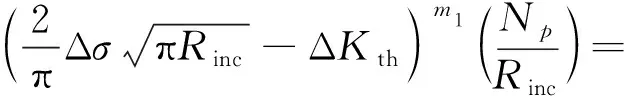
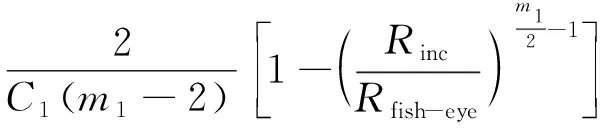
(5)

其中:Np为内部疲劳失效的预测疲劳裂纹扩展寿命。因此，对于由内部失效无FGA的裂纹扩展寿命模型如式(6)所示。

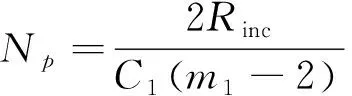
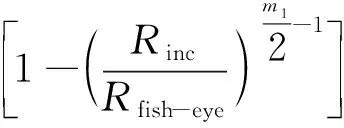
(6)

同理，对于由内部失效有FGA的裂纹扩展寿命模型如式(7)所示。

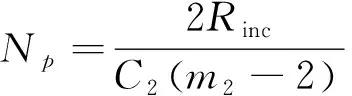
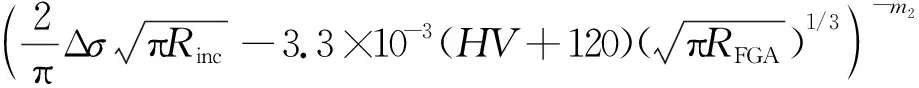
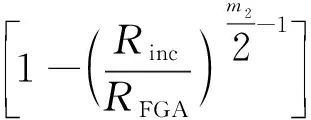
(7)

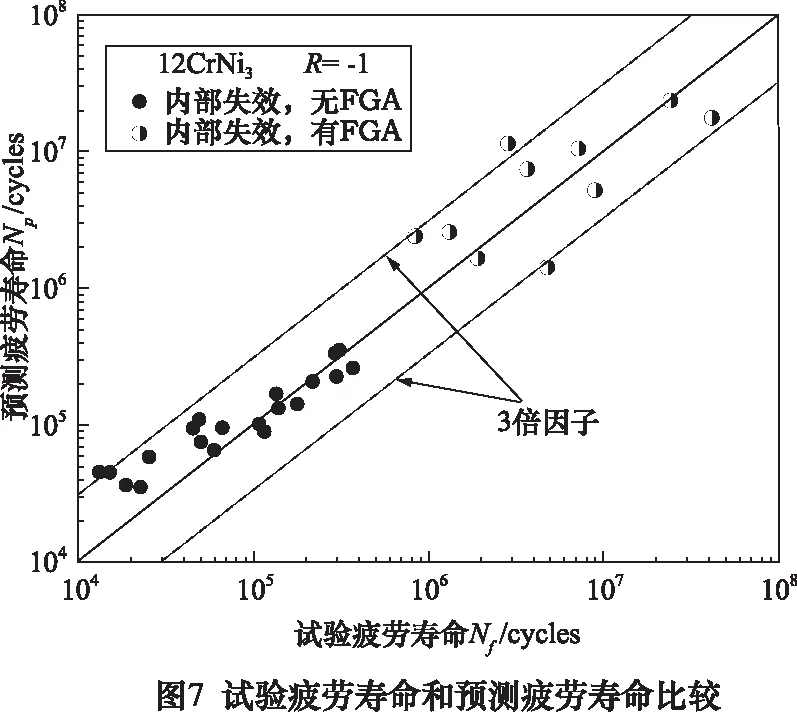
基于试验数据可得：C1= 3.389 3×10-15，m1=5.500 3；C2= 3.643 3×10-16，m2= 5.892 5。图7为试验疲劳寿命和预测疲劳寿命比较。由图可知预测疲劳寿命Np在试验疲劳寿命Nf的3倍寿命区间之内，这表明该疲劳寿命模型的预测精度较高。

4 变应力水平下疲劳残余寿命可靠性分析

4.1 基于威布尔分布的残余寿命分布函数

基于疲劳试验数据，发现32个试件疲劳失效的寿命值分散性较大。因此结合上文可定义一个新的变量：试验寿命比S，即S=Nf/Np，对S进行分布检验，可知S服从威布尔分布。则其概率密度为:

(8)

其中：N0为位置参数；Na为尺寸参数；b为形状参数。

结合Levenberg-Marquardt法，得到三参数威布尔分布的各个参数值为N0=0.78，Na=1.01，b=1.99。

在变应力水平下的零件，通常都可确定其最终的试验寿命比S。若零件工作一段循环周次且还未发生失效，此时试验寿命比定义为先验寿命ts。对于具有先验寿命ts的零件继续工作直到失效，此过程所损耗的试验寿命比定义为零件的残余寿命，记为Tt。Tt是随机变量，将其分布函数记为Ft(x)，则根据条件概率贝叶斯公式得[19]:

Ft(x)=P(Tt≤x)=P(T≤ts+x|T>ts)

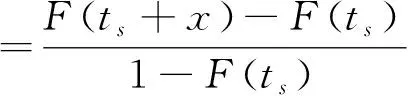
(9)

因为F(ts)=1-R(ts)，可知

F(ts+x)=1-R(ts+x)

(10)

将式(10)代入式(9)得

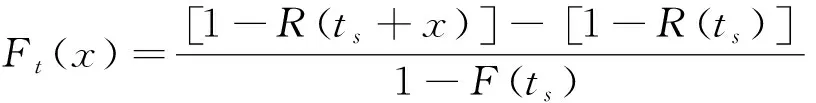
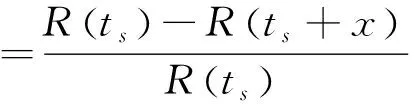
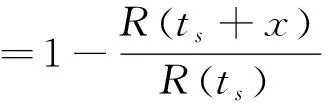
(11)

则一定先验寿命ts下的残余寿命的分布函数为:

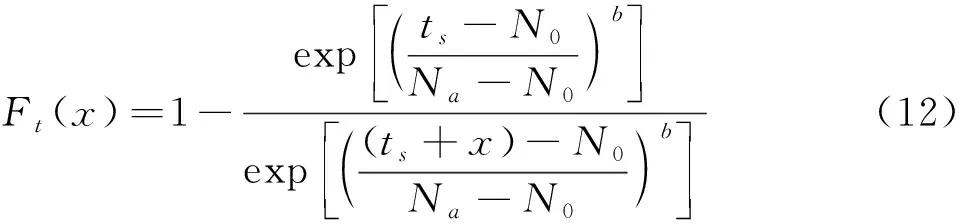
根据疲劳寿命的分布参数, 可以获取其残余寿命的分布规律。具有先验寿命ts的零件其残余寿命Tt能达到x的概率为:

(13)

一定先验寿命ts下残余寿命的概率密度函数为:

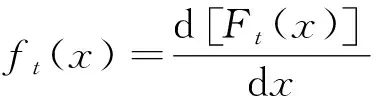
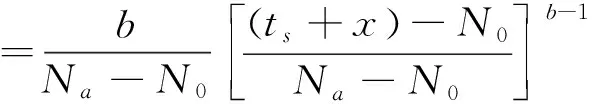
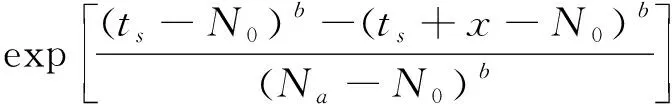
(14)

4.2 残余疲劳寿命可靠性评估

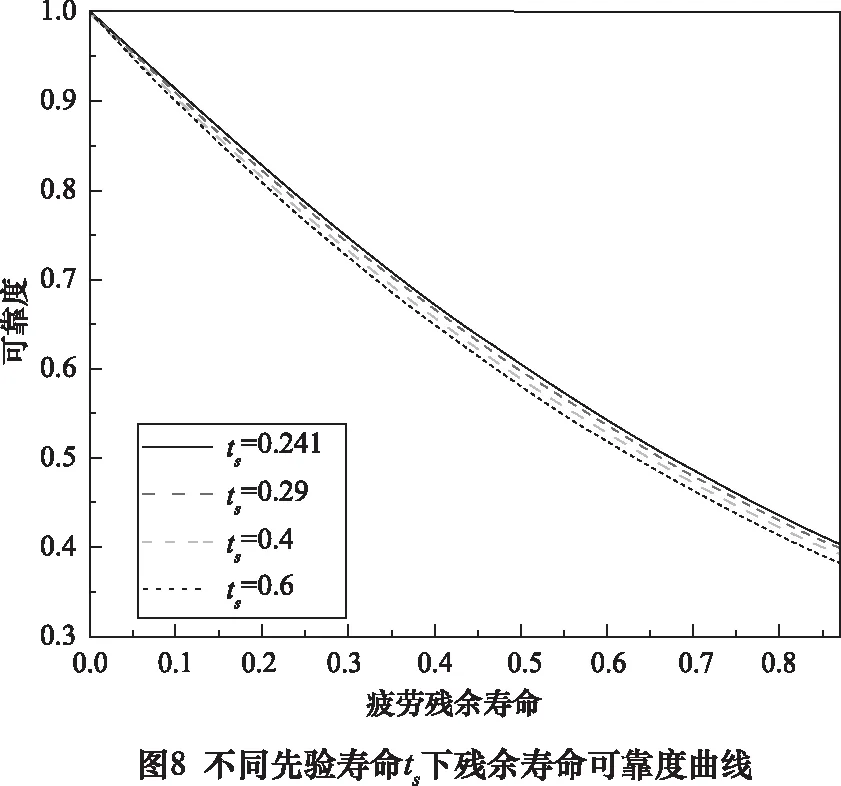
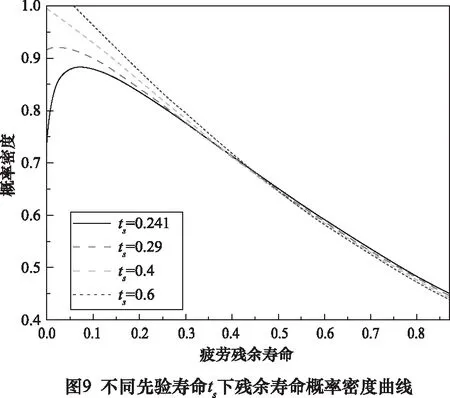
进一步地，当试样的先验寿命ts= 0.241, 0.29, 0.4, 0.6时，可分别计算得到残余寿命的可靠度和概率密度。

图8为不同先验寿命ts下残余寿命的可靠度曲线，图9为不同先验寿命ts下残余寿命的概率密度曲线。很明显，随着残余寿命增加，其可靠度在减小且减小趋势由大到小，因此可靠度曲线逐渐由陡变缓。其概率密度也在减小，并且残余寿命的分散性也越来越大。

5 结语

(1) 通过疲劳试验，得到了12CrNi3合金钢的S-N曲线，发现随着疲劳寿命的增加应力幅值在不断下降，并且不存在传统的疲劳极限。

(2)从疲劳裂纹扩展角度，基于裂纹尺寸特征，提出了疲劳寿命预测模型；该模型所预测的疲劳寿命在3倍寿命区间之内且有较高的预测精度。

(3)从概率角度，基于变应力水平下疲劳寿命的三参数威布尔分布规律，进一步构建了试样先验寿命下的残余寿命可靠度模型及概率密度模型。在不同先验寿命ts下，随着疲劳残余寿命的增加，其可靠度在减小且减小趋势由大到小；其概率密度也在减小，并且残余寿命的分散性也越来越大，与工程实际相符合。