考虑冲压作用的悬架控制臂疲劳强度分析

雷 刚 陈志豪 于 航 樊 伟

(①重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆400054；②浙江吉利汽车研究院有限公司，浙江 宁波 315336)

作为悬架系统的关键部件，控制臂起到导向和传力的作用，同时影响着车辆行驶的平顺性和操纵稳定性[1]。冲压成型因其低成本[2]、高精度和良好的材料利用率成为制造控制臂的主要方式之一[3]。在以往的CAE分析中常忽略成型因素对控制臂这类钣金件结构性能的影响，而在实际情况中冲压成型导致控制臂厚度分布不均匀，造成整体强度及疲劳性能降低，这就导致分析结果相较于实际情况误差大。

为了提高冲压件的仿真精度，国内外学者对此做了大量研究。Wang W L等人[4]通过一种数据库修改方法将冲压效应考虑到发动机支架的疲劳预测中，大大提高了疲劳预测的准确性。Mélanie C等人[5]解决了冲压工艺对部件疲劳性能的影响并阐明了在汽车部件生产过程中如何有效考虑这些影响。

本文以某款车型的麦弗逊悬架控制臂为研究对象，基于整车多体动力学模型，根据轮心六分力和轮胎接地力分别获取控制臂铰接点处的动静态载荷，对未考虑冲压效应与带有冲压效应的控制臂模型进行疲劳强度仿真对比。依据结果对冲压工艺进行改进并对改进后的冲压模型再次进行疲劳强度仿真，通过3次结果的对比分析，研究了冲压效应对控制臂疲劳强度性能的影响。

1 动静态载荷的获取

1.1 动态载荷谱的获取

比利时环路作为综合考量汽车耐久性可靠性的特殊路面[6]，是控制臂疲劳耐久测试的最佳选择。为了确保分析结果的可靠性，本文采用实际采集的方法，在汽车满载情况下，把车辆在比利时环路上获取的道路信号作为输入进行求解仿真，从而获取六分力数据。

基于获得的六分力谱，提取到此路面下控制臂3个连接点动态载荷谱如图1所示。控制臂外点与转向节之间采用球铰链接，因此只有3个方向的力。

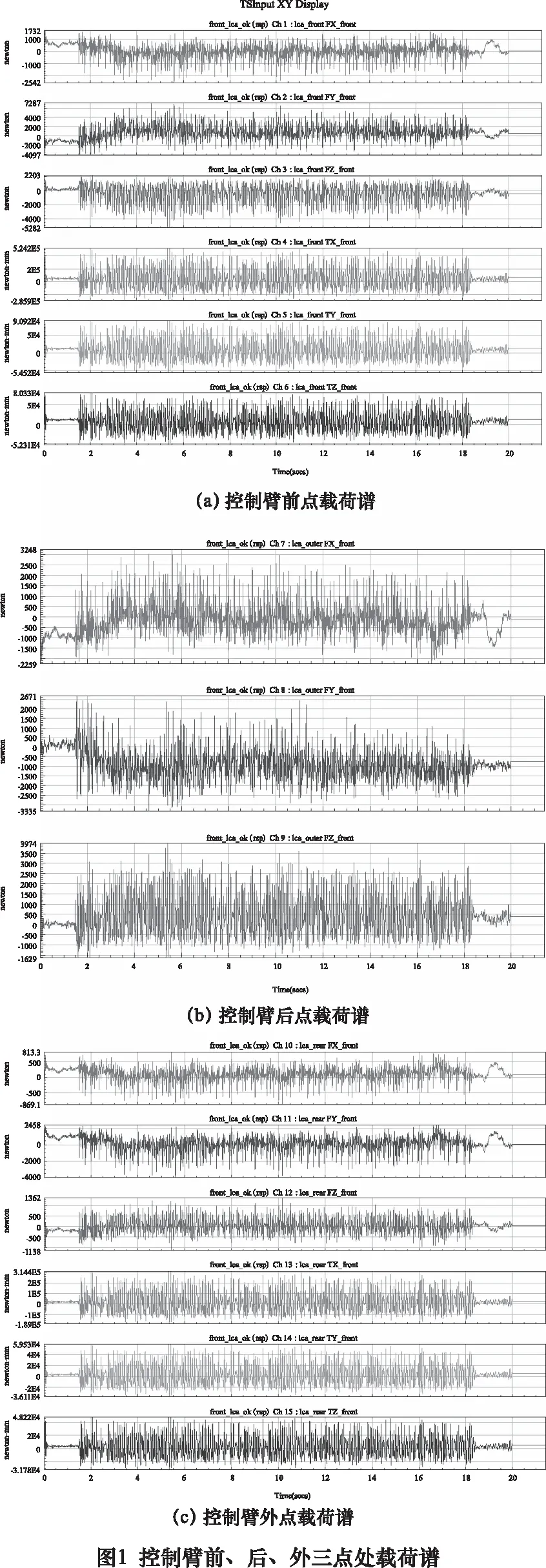
建立整车动力学模型，主要包括麦弗逊前悬架、双连杆后悬架以及转向系统等子系统，对各子系统进行装配，得到的整车多体动力学模型如图2所示。

1.2 静态载荷的计算

为了较全面的反应悬架在极限工况下的性能，计算紧急制动、通过不平路面以及极限转向工况下(取车辆右转状态)的轮胎接地力。这3种工况的加速度分别1g、3.5g、0.95g(g=9.81 m/s2)，所需的车辆相关参数如表1所示。

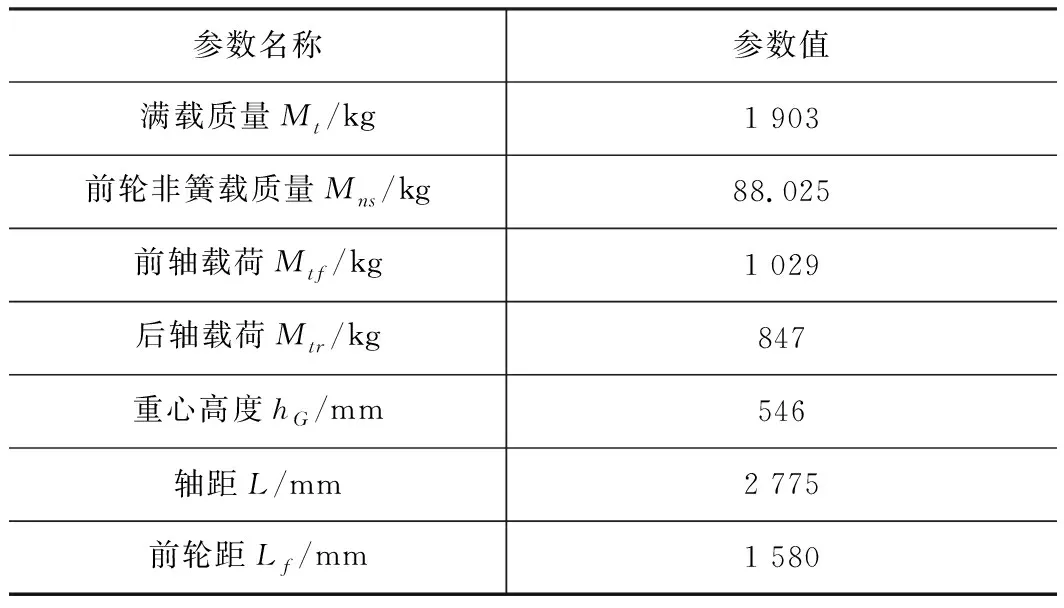
表1 车辆相关参数

通过计算获取到的3种工况下的车辆左右前轮接地力如表2和表3所示。将上述轮胎接地力输入悬架模型中进行仿真分析，得到各个典型工况下前悬架控制臂铰接点载荷如表4所示。

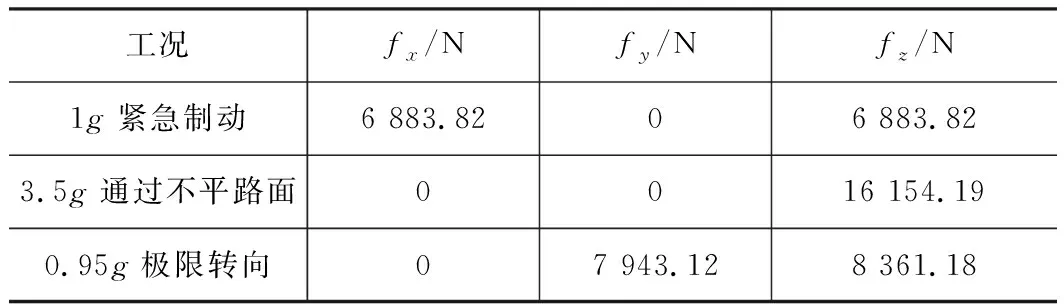
表2 3种工况下左前轮接地力

表3 3种工况下右前轮接地力

2 控制臂有限元建模及仿真分析

2.1 控制臂有限元建模

麦弗逊悬架控制臂由上中下3层板件构成，其厚度分别为3 mm、2.6 mm、3 mm，前后衬套厚度分别为4.25 mm与5 mm。采用抽取中面的方式进行二维混合网格划分，平均网格尺寸为4 mm，得到共计21 279个网格，21 367个节点。控制臂的材料为结构钢SAPH440，其弹性模量为2.07×105MPa，泊松比为0.3，密度为7.8 t/m3，屈服强度为305 MPa。在控制臂外侧球铰与转向节相连处以及内侧前后端衬套与副车架相连处采用RBE2单元进行模拟，在内侧衬套与板件之间等连接处采用二维单元模拟焊缝，控制臂有限元模型如图3所示。

2.2 边界条件及工况确定

在实际情况中，控制臂随着车辆的行驶而摆动，因此采用惯性释放的方式对控制臂进行约束，同时将表4得到的控制臂铰接点的载荷施加到3处RBE2单元从节点上。

表4 3种极限工况控制臂铰接点载荷

2.3 仿真计算

2.3.1 强度分析

仿真结果如图4所示。

由图4可知，3个工况下的应力主要集中在控制臂外缘拐角以及外侧螺栓孔附近，最大应力为极限转向工况下的控制臂外端，大小为286.2 MPa，而控制臂的屈服极限为305 MPa，安全系数大于1。在3种极限工况下，控制臂的最大应力小于其屈服强度，不会发生塑性变形和破坏，满足设计要求。

2.3.2 疲劳分析

由于控制臂的失效很大概率是因为高循环次数的交变载荷造成的，属于高周疲劳失效，因此采用名义应力法进行疲劳分析[7-8]。在此之前需要对控制臂施加单位载荷并求解，对控制臂前后端施加3个方向的单位力和力矩，对外端施加3个方向的单位力，共计15个工况，将计算后的控制臂单位应力结果输出并进行疲劳分析。控制臂的材料为SAPH440，根据其材料参数得到其S-N曲线如图5所示。

结合所得的控制臂外、前和后侧3处动态载荷谱对控制臂疲劳寿命进行预测，采用Gerber平均应力修正与Von Mises应力相结合的方式进行计算，得到的疲劳寿命云图如图6所示。焊缝处以及控制臂前端与外端衬套孔附近为疲劳寿命较小区域，其中节点ID为7 942处为疲劳寿命最小处，其寿命达到了3.006×105个载荷循环，换算为行驶里程则超过1.6×106km，远超《机动车强制报废标准规定》的6×105km里程数，因此发生疲劳破坏的可能性极低，满足要求。

3 控制臂冲压模型的建立及仿真分析

3.1 冲压模型的建立

对控制臂进行冲压仿真，为了使软件能根据模型实时细化网格以匹配变形较大的区域，确保一定的求解精度与速度，本文采用自适应网格划分方式继而将其进行偏置获得凸模网格模型。

3.2 冲压仿真参数设置与结果分析

为了避免出现冲压负角，先建立冲压局部坐标，再定义合理的拉伸方向，采用直接成型的方法，并对板件进行修边、冲孔和翻边，得到的成形极限与厚度变化结果分别如图7及图8所示，依据云图，控制臂最薄处为2.26 mm，位于外端及前端边缘处，相较于数模最大厚度的3 mm减少了0.74 mm，减薄率达到24.7%。

3.3 冲压结果映射与疲劳强度分析

对自适应网格进行重新划分并对成形结果调用与映射，得到不同厚度的控制臂模型，映射后的加载模型如图9所示。

对经过冲压仿真的控制臂模型进行强度分析，3个工况下的强度云图如图10所示，与未带有冲压效应的控制臂强度结果对比如表5所示。

表5 有无冲压效应的控制臂强度结果对比

根据云图以及表格可知，考虑冲压效应的控制臂在紧急制动与极限转向工况下最大应力值显著大于未带有冲压效应的控制臂且超过了材料的屈服极限，应力较大的区域依旧分布在控制臂外端球铰以及翻边处，不满足强度要求。

对带有冲压效的控制臂进行疲劳分析，其疲劳寿命云图如图11所示，由云图得，疲劳寿命较小区域集中在控制臂外端与球铰相连的螺栓孔附近，其疲劳寿命为2.146×105个载荷循环，即1.18×106km的行驶里程，虽然依旧满足设计标准，但相对于未考虑冲压效应的控制臂疲劳寿命缩短了28.9%，可见冲压效应能够对控制臂的结构性能造成较大影响。

4 冲压工艺的改进及对比分析

依据前文内容，具有冲压效应的控制臂其强度及疲劳寿命都有一定的缩减，特别是紧急制动和极限转向工况下的强度无法满足设计要求，这是由于冲压导致控制臂厚度分布不均，部分区域如控制臂前部衬套周围与翻边处减薄。初步分析是由于凹凸模圆角半径较小，使得进料不顺畅，要针对冲压工艺进行改进。对模的圆角半径进行增大以减小进料阻力，以降低冲压后的减薄率，再次进行冲压仿真，得到的成形极限和厚度变化云图如图12与图13所示。

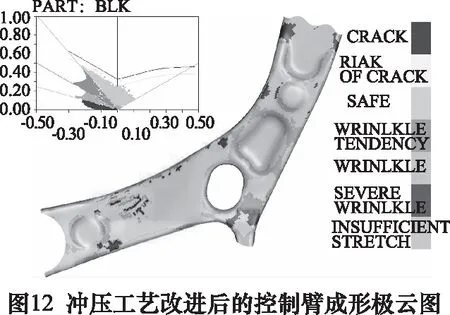
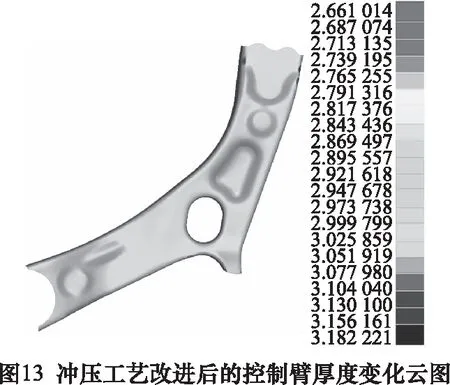
根据云图结果，控制臂最薄处为2.66 mm，其厚薄分布位置无较大变化，但相较于原结果24.7%的减薄率，优化后的减薄率降低至11.3%，有较大改善。将网格结果映射到冲压工艺改进后的有限元模型中进行强度分析，得到3种极限工况下的结果云图如图14所示。

从结果来看，改进后3种极限工况下的应力仍主要分布于控制臂翻边处，相较于改进前，3种工况的最大应力分别减小了5.6%、1.3%、8.3%，具体结果数据对比如表6与表7所示，最大应力值小于控制臂材料的屈服强度，基本满足要求，说明在冲压工艺改进之后，该工艺下的控制臂结构性能会得到优化，同时也验证了冲压工艺中造成的控制臂厚度的变化对控制臂的结构性能也存在不可忽略的影响。

表6 冲压工艺改进前与原结果最大应力结果对比

表7 冲压工艺改进后与原结果最大应力结果对比

对冲压工艺改进后得到的控制臂进行疲劳仿真，得到其疲劳寿命云图如图15所示。控制臂疲劳寿命较薄弱区域基本未发生变化，但其载荷循环由改进前的2.146×105增大到了2.563×105，增幅达到了19.4%，将其转换为行驶里程为1.42×106km，虽相较于未带有冲压效应的控制臂该值减少了14.4%，但依然远大于国际规定的6×105km的强制报废里程数，而且相比于冲压工艺改进前的疲劳寿命也有明显改善，这说明冲压工艺导致的控制臂厚度的变化必然对控制臂的疲劳寿命有较大影响。

冲压工艺改进前后控制臂疲劳寿命转换为行驶里程与原结果对比如表8所示。

表8 冲压工艺改进前后控制臂疲劳寿命与原结果对比

5 结语

本文研究了控制臂在传统有限元分析及考虑冲压成型作用下的强度及疲劳寿命，并针对第一次冲压仿真结果对冲压工艺进行优化，对比了3次仿真的控制臂疲劳强度，得到以下结论：

(1)冲压工艺使得冲压件不可避免的出现厚度不均匀、局部出现厚度减薄情况，导致带有冲压效应控制臂的强度及疲劳性能相较于未考虑冲压效应的控制臂有一定的下降，表明冲压成型对控制臂的强度及疲劳性能的影响不可忽视。在对控制臂这类冲压件进行有限元分析时考虑冲压成型对其厚度的影响可以提高仿真的精度，使得结果更贴合实际。

(2)优化冲压工艺如增大凹凸模圆角半径可以降低进料阻力，以减少出现局部厚度减薄的情况，降低冲压成型对零部件结构性能影响的程度。