基于ARMA—ARCH模型的上证指数波动率的实证研究
文/王萌月(中央财经大学金融学院)
一、前言
(一)研究背景
对于投资者和学者而言,预测股票交易指数是一个棘手的问题。股市是一个极度复杂的市场,其表现受到多种因素的影响,比如通货膨胀率、利率、经济环境、政治问题等。波动性是评估金融市场状况,是投资者、基金经理和金融监管机构做出决定的重要参考变量,是确定股票、期权和期货等金融工具价格的重要因素,是衡量风险与投资回报的一种方法。股票市场的波动性对金融法规、货币和财政政策也有重大影响。预测波动性已经成为经济活动中十分重要且迫切的事情。使用适当的预测模型,可以通过非常准确地预测来获得巨大的回报,这就关系到所构建预测模型的准确性问题。因此,选择什么模型、什么指数更具有代表性,成为广大学者致力于研究的问题。
(二)模型基本理论
ARMA模型和ARCH模型是预测波动率的经典模型。
1.ARMA模型
ARMA模型称为自回归移动平均模型,是时间序列分析模型的一种。是将AR(p)模型(自回归模型)和MA(q)模型(移动平均模型)组合,得到ARMA(p,d,q)模型。表达式如公式1-1:

2.ARCH模型
另一个时间序列分析常用模型为ARCH模型,称为自回归条件异方差模型,广泛应用于与波动性有关的研究,还可以度量金融风险的大小。通常研究波动率聚类性特征,波动率聚类是由于金融资产收益率可能日收益率不存在或自存在微弱的自相关性,但是收益率的平方存在很强的自相关性,即收益率序列不相关但是也不独立。ARCH(q)模型表达式如公式1-2:

随着ARCH模型的不断发展出现了ARCH类模型,包括GARCH,EARCH,TGARCH,ARCH—M模 型,这些模型均被广泛运用到波动率预测中。
二、文献综述
(一)国外相关文献
Engle,Robert(1982)针对尖峰厚尾的金融数据提出了具有良好拟合效果的ARCH(p)模型,为股票市场价格的自回归条件异方差问题提供了解决工具。Tim(1986)发现ARCH模型并不能很好地拟合所有的时间序列,便在此基础上加入了带有滞后期的条件方差误差项,GARCH模型应运而生。Robert,Mustafa(1992)认为GARCH模型处理厚尾能力强,能有效解决小样本背景下模型阶数过大造成的低效率和低精度问题,更加准确地描述条件异方差的动态特征。
(二)国内相关文献
贺本岚(2008)以2001年1月到2008年1月的上证指数为样本,对数据进行时序分析,在研究过程中分析比较了ARMA模型和ARCH模型,他发现自回归条件异方差模型能更好地预测波动率。成城(2014)选取1998—2013年上证指数的数据为样本进行量化分析,他在研究过程中用ARCH类模型进行了对比研究,证明了ARCH类模型中的GARCH模型和EGARCH 模型在研究波动率方面的可行性。姜海凤(2014)以我国饮料行业板块为研究对象,用ARCH类模型研究了该板块的波动率特征,并 对ARCH,GARCHE,EGARCH模型进行了比较。发现了我国饮料行业波动率具有尖峰厚尾、聚类等异方差特征。
三、上证股指波动率实证研究
(一)数据预处理
本文以上证指数作为时间序列,样本时间跨度为2016年1月4日至2020年5月30日,共1065个数据。为了考察ARMA—ARCH模型在估计并预测上证股指波动率方面的准确性,本文将样本空间分为两个部分,即估计样本和预测样本。2016年1月4日至2020年4月30日为估计样本,用于模型参数估计,2020年5月1日至5月30日为预测样本,用于评价所构建的ARMA—ARCH模型的预测能力。本文数据来源于wind金融终端。
1.平稳性检验
平稳性是分析时间序列数据的前提,检测样本的平稳性,主要有两种方法。第一种方法是图检法,根据时间序列数据的走势可以直接判断是否平稳。从图1中我们可以看到,上证股指的收盘价在2016年1月初有一个陡然下降的趋势,从2016年2月到2017年底逐渐震荡上升。到了2018年初达到高峰,之后急剧下降,在2019年初降到最低点。随后在2019年年中,2020年初均出现小高峰。很明显,该时间序列数据是非平稳的。为了消除主观因素的影响,更加准确地验证该组数据是否平稳,我们用平稳性检验的第二种方法:ADF单位根检验,结果如表1所示,t统计量的值为-1.572,其绝对值明显小于在1%,5%以及10%的显著性水平下的t统计量的绝对值,所以我们可以得出上证指数收盘价序列至少存在一个单位根,所以该时间序列是非平稳的。

表1 上证指数日收益率序列单位根检验

图1 上证指数日收盘价时序图
2.平稳化处理
为了消除上证指数时间序列的异方差实现平稳化,我们需要进行平稳化处理,实现平稳化的方法有两种,一是取对数,二是做差分。为了进一步保证平稳,我们同时采用这两种方法,即采用对数差分法进行处理,用相邻两日收盘价的对数一阶差分表示,公式可以表示为DP=lnpt-lnpt-1, pt,pt-1分别表示t和t-1时刻上证指数的收盘价。
如图2所示,我们可以看出对数一阶差分之后的时序图在0附近上下波动,且没有明显的趋势,因此对数差分之后的时间序列数据是平稳的。同样的,为了更加使该结论具有说服力,我们进行ADF单位根检验,检验结果如表2所示,t统计量的值为-12.805,其绝对值明显大于在1%,5%以及10%的显著性水平下的t统计量的绝对值,所以我们可以得出上证指数收盘价序列不存在单位根,此时的时间序列是平稳的。

表2 上证指数对数差分后的单位根检验

图2 上证指数对数差分后的时序图
(二)模型构建
1.ARMA模型
(1)ARMA模型定阶
在第一部分中,我们通过对数一阶差分之后已经将时间序列进行了平稳化处理,下面我们通过建立ARMA(p,d,q)模型来进行参数估计,该模型的关键就是定阶,即p、d、q的值,我们已经知道d=1,现在来确定p和q的值。通过表3我们可以看到自相关和偏相关在4阶截尾,我们大致估计p=4,q=4。为了进一步确认,我们根据AIC最小准则进行反复试验,发现在p=4,q=4时,AIC确实最小。因此我们可以建立ARMA(4,1,4)模型对参数进行估计,拟合结果如表4所示,我们可以发现除了常数项,其他参数的P值均小于0.01,说明在1%的显著性水平下这些参数都是显著的。根据表4我们可以得出ARMA模型的表达式,即公式1。
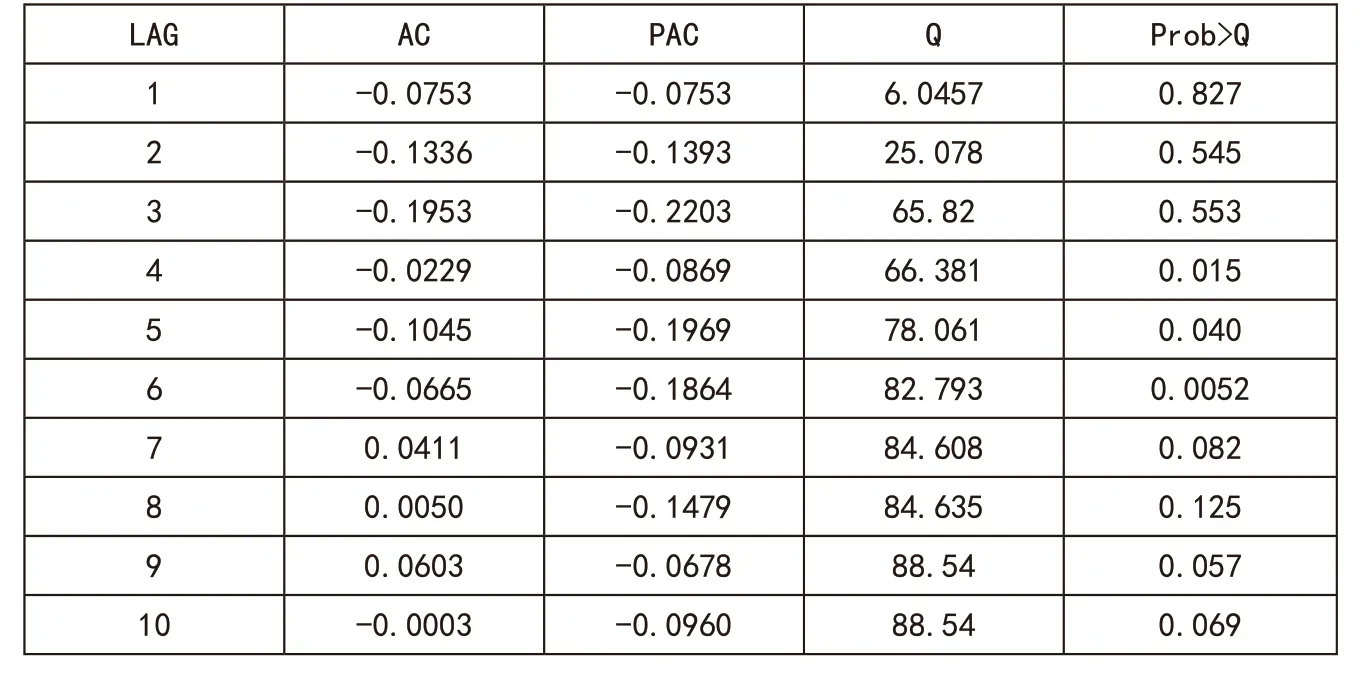
表3 上证指数自相关和偏相关表

表4 ARMA(4,1,4)模型参数估计结果

(2)模型检验
为了对构建的ARMA(4,1,4)模型进行检验,即检验该模型残差序列是否为白噪声,我们对残差进行检验。我们通过观察ARMA(4,1,4)模型的自相关和偏相关图,如表5,根据结果显示我们构建的这个模型的自相关和偏相关的p值均大于0.05,由此我们可以认为该模型通过了检验。
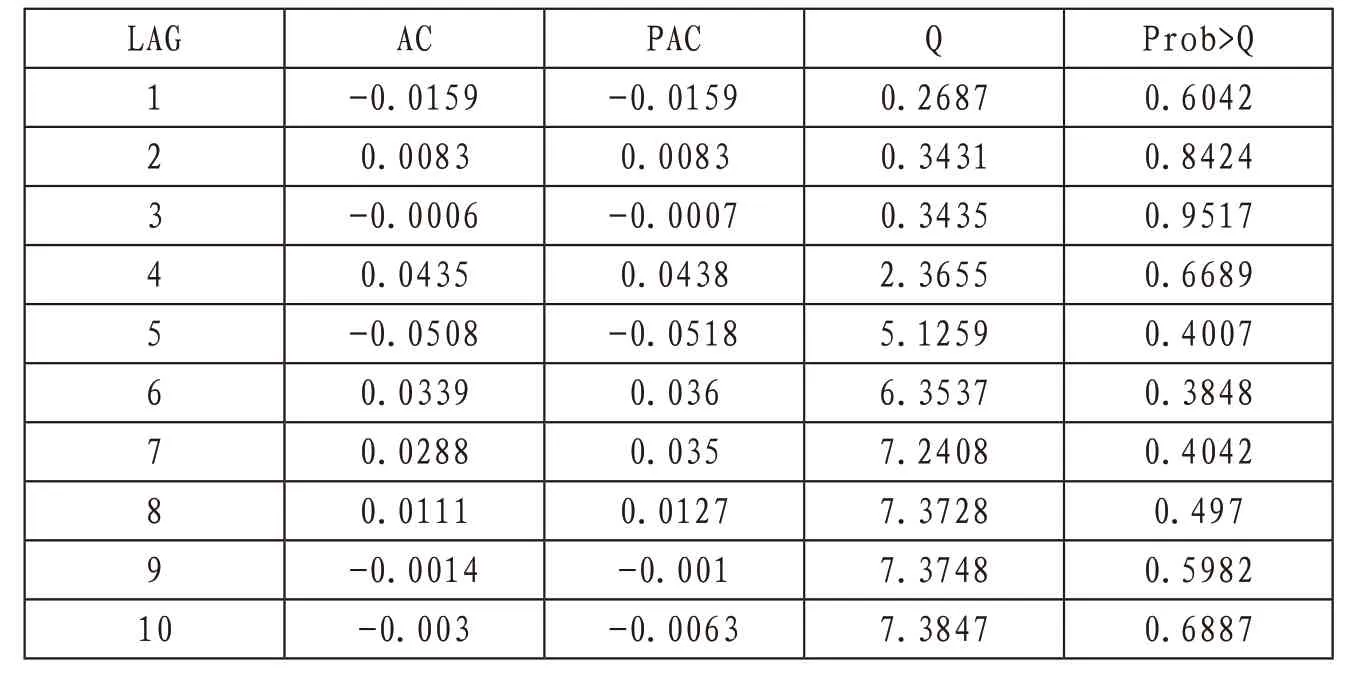
表5 ARMA(4,1,4)模型自相关和偏相关表
2.ARCH模型
(1)ARCH模型定阶
在构建了ARMA(4,1,4)模型的基础之上,为了防止残差序列存在条件异方差给预测结果造成影响,我们需要建立ARCH类模型来消除条件异方差。同时根据上图3我们观察到上证指数对数差分之后的时序图呈现波动率聚类的特点,同时我们通过软件计算出了这组数据的偏度和峰度,峰度大于3意味着我们需要进一步建立ARCH类模型。或者我们可以通过对残差方差进行预测,通过观察方差时序图,即图3发现,存在明显的条件异方差,所以我们需要建立ARCH类模型。
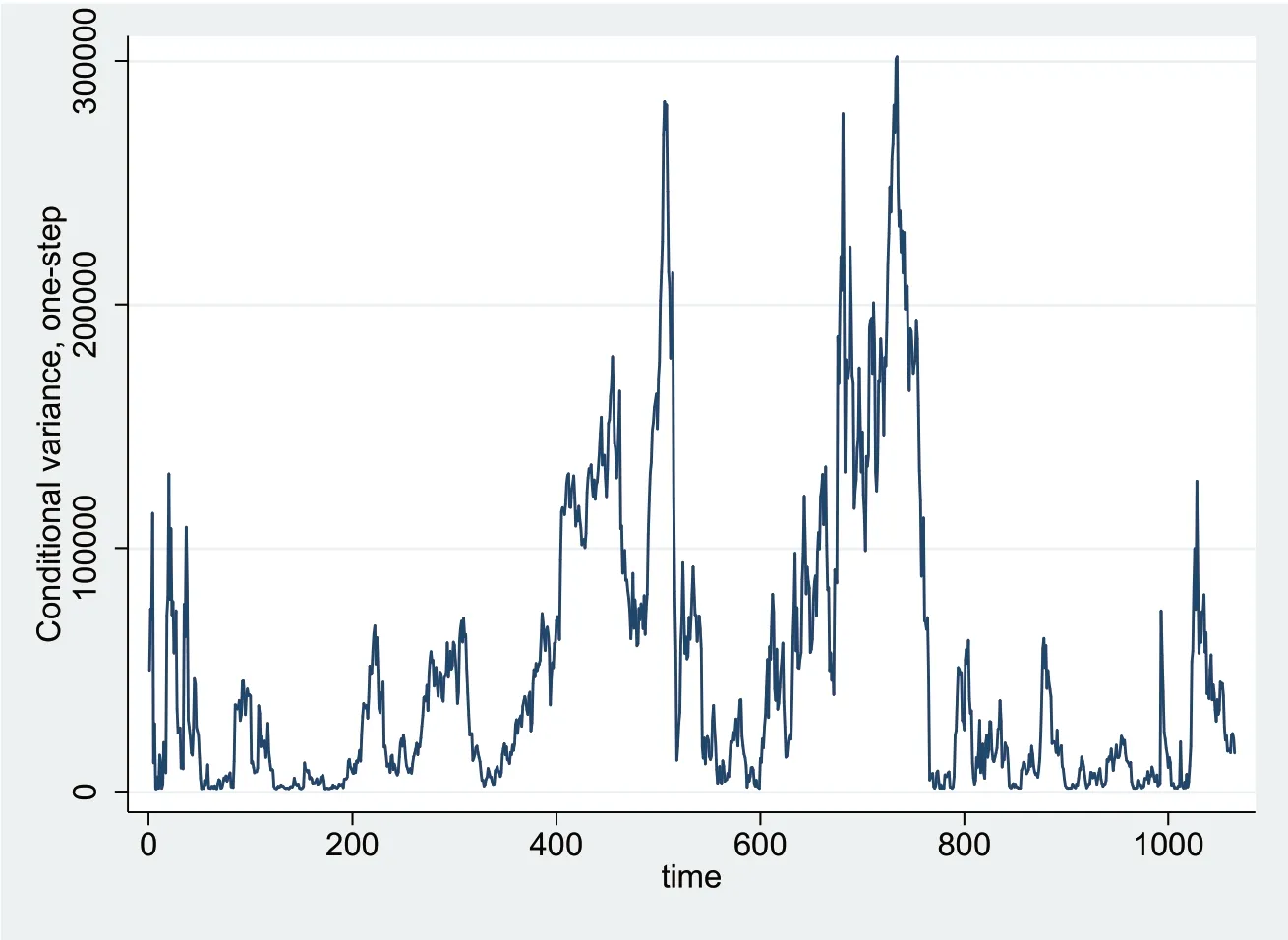
图3 上证指数残差的方差时序图
建立ARCH模型同样关键的是要确定阶数,我们需要进行不断重复的试验。首先建立ARCH(1)模型,通过自相关和偏相关的P值发现,该值均小于0.05,所以仍然存在自相关。这说明我们建立的ARCH(1)模型阶数不够。经过不断试验我们发现ARCH模型在滞后3阶时模型的自相关和偏相关系数等于两倍标准差,其他均处于两倍标准差之内,所以在ARMA(4,1,4)模型的基础上我们确定了ARCH(3)模型,称为ARMA-ARCH模型。
(2)ARMA-ARCH模型检验
我们通过自相关和偏相关系数的P值对该模型进行检验,如表6所示,我们发现P值均大于0.05,说明我们构建的ARMA-ARCH模型的残差序列是一个白噪声,该模型通过了检验。

表6 ARMA-ARCH模型的自相关和偏相关表
(3)对ARMA-ARCH模型进行参数估计
根据ARMA和ARCH模型的定义可知,ARMA模型是通过时间序列的均值进行拟合,ARCH模型是通过时间序列的方差进行拟合,根据表7的模型参数估计结果,我们可以得出如下两个方程:

表7 ARMA-ARCH模型参数估计结果
均值模型:

方差模型:

(三)模型预测
根据前面内容,我们将样本分为了两个部分即参数估计样本和预测评价样本,我们将2016年1月4日至2020年4月30日的数据称为样本内,将2020年5月1日至5月30日的数据称为样本外。用ARMA—ARCH模型对样本外的数据进行预测,预测结果见表8。

表8 真实值与预测值比较
从表中我们可以得出误差比均小于10%,相对来说预测值和真实值还是比较接近的,但是我们发现5月19日和5月20日的误差比均超过了5%,因此该模型在短期的预测效果较好,但是不太适合长期预测,随着预测周期变长,误差会越来越大。
四、结论
本文建立了对上证指数波动率定量研究的ARMA-ARCH模型,根据该模型的预测结果,我们发现短期预测效果较好,长期预测误差会增大。且在研究中我们发现上证指数波动率较大并且具有尖峰厚尾、聚类性等条件异方差特征。为了我国股市的健康发展,对于投资者来说应该保持理性思维,尽量避免盲目跟风;对于上市公司来说,应该及时披露经营和财务信息,尽量做到信息透明;对于监管部门来说,应该加大对内幕交易、财务造假等行为的惩罚力度,积极构建一个公开、公平、公正、透明的股票市场。同时应该严格审核IPO,完善劣质上市公司退出机制,提高上市公司质量,只有这样才能实现资源配置效益的最大化。

