转换角度看问题 拨云见日疑惑开

李晓阳

中图分类号：G4 文献标识码：A

从小学到中学数学知识，呈现一个有益到难、从简到繁的过程。然而，人们在学习数学理解和掌握数学的过程中，却经常通过把陌生的知识转化为熟悉的知识，把繁难的知识转化为简单的知识，从而逐步学会解决各种复杂的数学问题。因此，转化既是一般化的数学思想方法，具有普遍的意义，同时转化思想也是攻克各种复杂问题，法宝之一，具有重要的意义和作用，转化思想的实质，就是在已有的简单的、具体的基本的知识的基础上，把未知化为已知，把复杂化为简单，把一般化为特殊，把抽象化为具体，把非常规化为常规，从而解决各种问题。现就把我自己在小学数学课堂中如何渗透转化思想的和大家一起分享下。

一、化新为旧，把陌生的问题转化为熟悉的问题。

任何一个新知识，总是原有知识发展和转化的结果。在实际教学中，我就引导学生把感到生疏的问题转化成比较熟悉的问题，并利用已有的知识加以解决，就是我们所谓的化未知为已知，促使其快速高效地学习新知。如空间与图形中的平行四边形、三角形、梯形等图形的面积公式推导，教学这些内容，一般是将要学习的图形转化成已经学过的图形，再引导学生得出新的图形的面积计算。

例如，平行四边形的面积推导，当教师通过创设情境使学生产生迫切要求出平行四边形面积的需要时，可以将“怎样计算平行四边形的面积”直接抛向学生，让学生独立自由地思考。这个完全陌生的问题，需学生调动所有的相关知识及经验储备，寻找可能的方法，解决问题。当学生将没有学过的平行四边形的面积计算转化成已经学过的长方形的面积。其他图形的教学亦是如此。1、推导三角形面积时，把三角形转化成平行四边形。 2、推导圆的面积公式时，把圆形转化成长方形。3、推导圆柱体积公式时，把圆柱体转化成长方体。4。圆锥的体积公式进，把圆锥转化成圆周柱。还有在求不规则图形和组合图形的面积，也是通过分割和割补把其转化为我们学过的规则图形，再通过它们的面积之和或之差来求。

另外在小数除法中，除数是小数的除法，也是把除数（小数）转化为整数，使其转化为学生熟悉的除数是整数的除法从而进行计算，笔算多位数乘除多位数，也是用的化新为旧的方法。

二、化抽象问题为直观问题，降低理解难度，帮助学生形成概念。

数学的特点之一就是它具有很强的抽象性，而对于小学生来说抽象的问题解决起来比较困难，而把抽象的问题转化为直观问题，将会大大降低理解难度。例如：教学"体积"概念。教师可以借助形象物体设问，引导学生分析比较。首先观察物体，初步感知。让学生观察一块橡皮和铅笔盒，提问：哪个大，哪个小？又出示一个魔方和一个骰子。提问：哪个大，哪个小？通过观察物体，让学生对物体的大小有个感性认识。接着在一个盛有半杯水的玻璃杯里慢慢加入一块石头，学生可以观察到，随着石头的投入，杯中的水位不断上升。问：玻璃杯里的水位为什么会上升？学生从这一具体事例中获得了物体占有空间的表象。在教师的引导下，对"为什么玻璃杯里的水位会随着石头放入而升高"这一问题进行深入讨论，通过讨论交流学生能够很自然地领悟"物体所占空间的大小叫体积"这一概念。为了进一步使概念在应用中得到巩固，继续在盛满水的玻璃杯里放石子，学生观察到水溢了出来，教师启发学生：从观察到的现象中你们发现了什么问题？学生思考后提出：杯里溢出的水的多少与放进去的石子有什么关系？经过讨论得出：从杯里溢出水的体积等于石子的体积。至此学生不仅认识了概念，而且能够应用概念。

三、化繁为简，使问题简单化。

化繁为简，如同侦破谜案，追踪迷雾后面简单的真相。数学问题看似复杂多变，像谜案一样让人猜不透.其实谜案背后的动机往往并不复杂。学数学、做数学题，正是追踪复杂表象背后的简单性，往往从已有的基本事实或原理出发，抓住蛛丝马迹，穷追不舍，直到水落石出，柳暗花明`。

例如：在教学植树问题时，出示例题：同学们在全长200m的小路一边植树，每隔5m栽一棵（两端都栽）。一共要栽多少棵树？

引导学生理解题意，大胆猜测，并开始验证时。看来这个问题值得我们研究，可200米有点长，研究起来不方便，怎样才能使我们的研究更方便呢？把小路缩短，我们就将原来的复杂的问题变得简单了。那下面我们就将小路缩短到20米来研究。這时，学生在转化思想的影响下，茅塞顿开，将一道生活中的数学问题既形象又有创意地解决了。从这里可以看出：有些问题比较复杂，直接解答过程会比较繁琐，我们可以化繁为简，从而使问题简单化。

四、化曲为直，化立体图形为平面图形，突破空间障碍。

“化曲为直”的转化思想在推导圆的面积公式中可以说把它运用的淋漓尽致，它可以把学生的思维空间引向更宽更广的层次，形成一个开放的思维空间，为学生今后的发展打下坚实的基础。

例如，圆面积的教学，我在教学过程中，先请学生把圆20等分以后，请他们动手拼成近似的平面图形长方形，学生发现分的份数越多，拼成的图形越接近长方形，圆的面积就等于拼成的长方形的面积，拼成的长方形的宽就是圆的半径r，长方形的长就是圆的周长的一半（πr）从而推导出圆的面积公式，即用转化思想，通过“化曲为直”来达到化未知为已知。学生兴趣盎然。

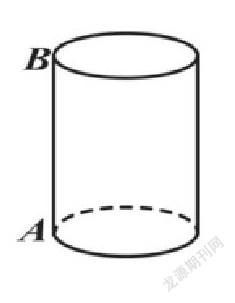
还有下面这道题目，是把立体图形转化为平面图形，大大降低题目的的难度。

如图，有一个圆柱形油桶，它的高为80分米，底面半径为25分米，在圆柱下底面圆周的A点有一只蚂蚁，它想吃到上底面与A点在同侧的B点的食物，要求蚂蚁只能沿桶壁爬行至少一周，则蚂蚁需爬行的最短路程是多少？（π取整数3）

此题只需要把圆柱展开，求A、B两点之间的距离就行了。

四、化数为形，降低解题难度。

数和形之间是对立又统一的关系。在一定的条件下可以相互转化。

例如，在教学"学校六月份用水210吨，比五月份节约了15%。五月份用水多少吨？"这一例题时，有学生列的算式是210÷（1+15%），有的学生列式为210÷（1-15%），而且争论的脸红耳赤，当我和学生一起把线段图画出来之后，学生的争论也就戛然而止了。因为有了线段图的合理支撑，学生对210÷（1-15%） 这一算式已坚信不疑了。可见，通过画线段图即数形结合的方法能有效将题目中抽象的数量关系直观形象地表示出来，从而降低解题难度。而根据学生的实际情况适当采取先数后形的策略，可以使学生的学习主动性大大增强，同时使学生的逻辑思维能力不断得到锻炼。

转化思想作为最重要的数学思想之一，在学习数学和解决数学问题的过程中无处不在，就要要求老师在课堂中把这一思想贯穿始终，学生才能熟练运用转化思想，解决各种复杂的问题，最终达到在数学的世界里举重若轻的境界。