多径信道下的改进型OFDM 定时同步方法

姚远翔，马文峰，曹 逊，吴 霞，赵几航

（陆军工程大学，江苏 南京 210000）

0 引言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）是多载波数字调制方案，广泛运用于Wi-Fi、4G 和5G 等通信系统中；但是由于OFDM 系统对定时和频率偏移的敏感性，它比单载波系统要求更高的同步精度。由于任何同步错误都会引入载波间干扰（Inter-Carrier Interference，ICI）和符号间干扰（Inter-Symbol Interference，ISI），从而降低OFDM 系统的性能；因此，同步是OFDM系统必须执行的一个重要步骤。目前实际系统中大多采用基于训练序列的同步算法，这是因为此类算法在前导结构上灵活多变，可以采用不同特性的序列构造前导。并且，此类算法针对不同结构可利用不同的相关处理方式，可以从多种角度对算法进行改进以不断提升同步估计性能。现阶段提出的同步方法主要有基于延迟自相关、基于对称自相关、基于本地序列互相关[1]3 种方法。其中，最经典的方法是由Schmidl 和Cox 提出的基于延迟自相关的[2]施米德尔-考克斯（Schmidl-Cox，SC）算法，该算法基于[A，A]训练符号结构，通过计算前后两个相同部分的相关峰值来确定起始点；但其定时测度函数在正确定时点附近有一个平台，这个平台导致帧起始点的模糊，增大了估计的误差。Minn[3]提出了一种改进的基于[A，A，-A，-A]训练符号结构的定时算法，这个方法的最大优点是在定时时刻减小了峰值平台；但是在错误时刻也很容易出现多个较大的尖峰，为判决门限的选取带来困难。随后Park[4]设计了一种新的共轭对称结构的训练符号，与Schmidl 和Minn 相比，它在正确的起始点产生了更清晰的定时度量，但仍然存在小的旁瓣。恒包络零自相关（Constant Amplitude Zero Auto Correlation，CAZAC）序列是一种具有恒幅值、零自相关等良好特性的同步序列，基于此，Malik[5]提出了利用由两个共轭CAZAC 序列组成的特殊前导码，并使用本地序列进行互相关的同步方法。Fang[6]、Jian[7]和Fan[8]分别又提出了不同算法来提高同步性能，但在多径衰落信道下的性能有待提高。Yang[9]提出了一种基于本地序列互相关、快速定时搜索窗口和双阈值决策的定时同步方法，有效地降低了虚警概率和捕获丢失概率，在多径信道下有较好的同步性能；但是其算法在定时测度旁有两个侧峰。

本文提出了一种基于扎多夫-楚（Zadoff-chu，ZC）序列的定时同步方法，该方法定义一种新的训练序列结构，使用本地序列互相关，可以有效地削减定时度量侧峰。此外，提出动态阈值判别法，以提高多径衰落下同步的鲁棒性。最后，通过仿真，在多径信道下，验证了其性能。

1 OFDM 系统模型

OFDM 的时域样本可以表示为：

式中：j为复数；n为子载波的总数；Nμ是有效子载波的数量；X(k)为在第k个子载波上传输的频域中的数据符号；x(n)为时刻n处的符号样本。

多径信道可以表示为：

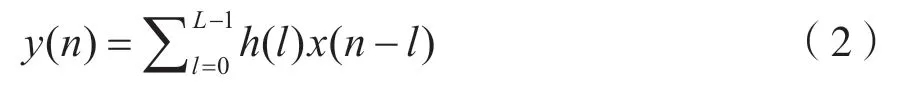
式中：h(l)为信道冲激响应；l为时域中信道样本的最大延迟。

所以，经过信道后接收机接受到的信号可以表示为：

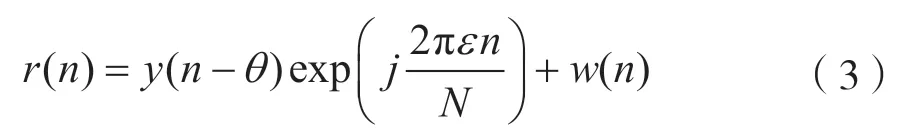
式中：θ为测量的整数符号定时偏移；ε为子载波间隔归一化后的载波频率偏移；w(n)为加性高斯白噪声（Additive White Gaussian Noise，AWGN）。

定时同步的目的是利用循环前缀或特殊训练符号的相关特性来估计延迟。由于如式（3）所示的AWGN 和多径的影响，同步方法需要对噪声和多径影响具有鲁棒性。

2 本文提出的同步方法

2.1 同步前导码设计

ZC 序列是CAZAC 序列的一种，也就是说它是恒幅值，零自相关序列，由Zadoff 和Chu 两人提出。该序列均峰比小，和自己的非整周期移位序列的相关值为0，而且两个互质的ZC 序列的互相关也接近于0。此外，它的傅里叶变换仍然是CAZAC 序列，所以该序列非常适合作为前导码来使用。

ZC 序列的表达式为：

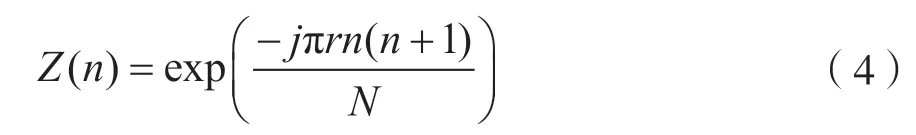
式中：r为序列根索引（root index）；N为ZC 序列的长度。两个根如果是互质的，那么生成的两个序列相关峰值几乎为零，所以本文利用这些性质设计了一种如图1 所示的新的训练序列结构。

图1 训练序列结构

该训练序列由1 个长度为N的OFDM 符号组成，其中A为一个长度为N/4，根索引为ra的ZC 序列。

由于快速傅里叶逆变换（Inverse Fast Fourier Transform，IFFT）不改变CAZAC 序列的性质，因此可以直接使用A或A的N/4 点IFFT 生成的序列来构造A。

B是和A对称且共轭的序列。

C是一个长度为N，根索引为rc的ZC 序列，其中rc和ra互质。

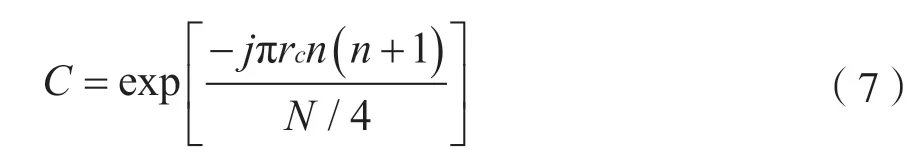
而D是和C对称且共轭的序列。

2.2 度量函数

根据所提出的前导符号的结构，定时度量函数被定义为：

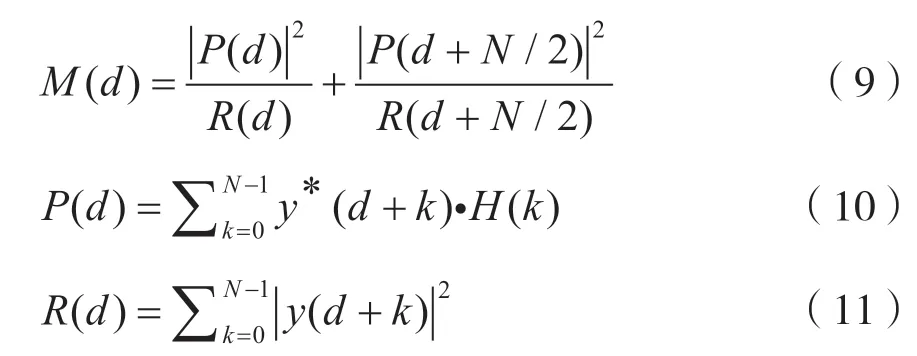
式中：P(d)为接收序列y和本地序列H之间的相关运算；R(d)是接收样本的模值，用来归一化。

图2 为在AWGN 信道下，SNR=0 dB 时的定时度量，可以明显看出在正确定时位置的度量值远超其他时刻。图3 为相同条件下Yang 算法的定时度量。

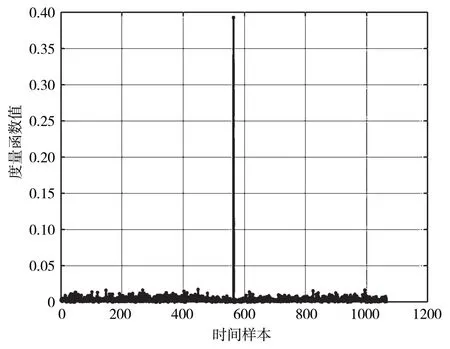
图2 本文方法的定时度量

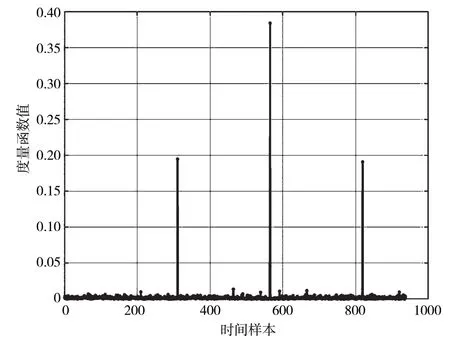
图3 Yang 算法的定时度量

从和图3 中Yang[9]的算法的比较可以看出，本算法有效地消除了正确定时时刻两侧的侧峰，这能够有效抑制多径信道下，低信噪比时，侧峰对正确判别带来的影响。

2.3 同步方案

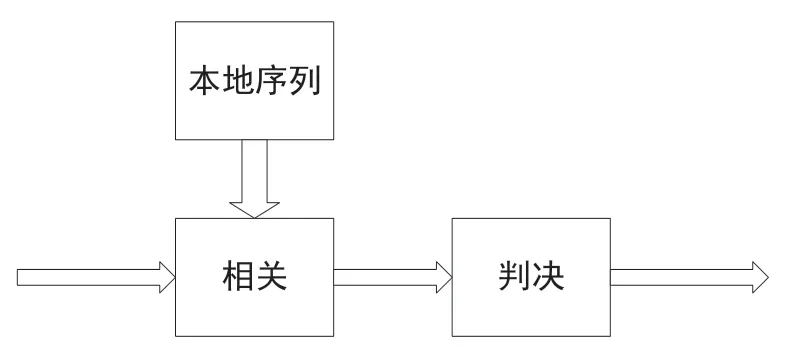
图4 同步方案

本文采用本地序列相关的方法，本地序列没有经过多径信道的传输，不会受到干扰，可以保证互相关获得更稳定的定时度量。在实际系统中，OFDM 受到多径和多普勒频移的影响。多径衰落可能导致同步位置的改变，多普勒频移可能导致信道的时间选择性衰落；结果，导致不同时隙上的接收信号强度不同，前导码的相关峰值将遭受不同的衰落系数。对此，本文提出了动态阈值的方法，不再采取单一的阈值来判别正确定时位置，而是根据相关值遭受的衰落，采取不同的阈值，极大地提高了判别的准确程度。

设当前样本点为d，首先对判决点前长度为100 个样点的滑动窗内的度量取平均值得到Ma，平均值Ma乘以系数g即可得到动态阈值Th1。再对判决点后100 个样点的滑动窗内的度量值取平均值得到Mb，平均值Mb乘以系数g即可得到动态阈值Th2。系数g可以根据信道的不同进行调整。在当前样本的度量值同时大于动态阈值T1和T2时，即认为该样本是正确的定时位置。即为正确定时时刻。

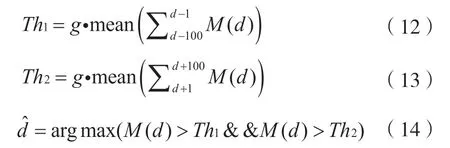
3 仿 真

本文采用MATLAB 进行多径衰落信道下的仿真，因为Yang[9]的方法比Malik[5]、Park[4]等的方法性能要好，所以本文和Yang[9]的方法进行对比。本文使用的是具有64 个循环前缀的256 个子载波的OFDM 符号。

在无线通信系统中，信号从发射端发射出来后，会在多个信道下进行传输，可能会经过地面、建筑物的反射、折射、绕射等，最后才会到达接收端。在接收端，这些带有同样信息的信号由于信道的不同，相应地，到达接收端的时间以及信号强度等也会不同。另外，在移动通信系统中，终端难免会有移动速度，根据物理学中的多普勒效应，会产生多普勒频移。对此，第三代合作伙伴计划（3rd Generation Partnership Project，3GPP）协议中定义了几种不同的信道仿真模型来对多径衰落以及多普勒效应等进行信道模型的仿真。

本文采用的多径衰落信道模型为3GPP 标准下的扩展典型城市信道（Extended Typical Urban，ETU）模型，扩展步行者信道（Extended Pedestrian A，EPA）模型和扩展车辆信道（Extended Vehicular A，EVA）模型。

ETU 模型总共有9 条路径。每条路径分别有不同的延迟和增益。本文模拟了典型的城市中的多径衰落信道。具体参数如表1 所示。

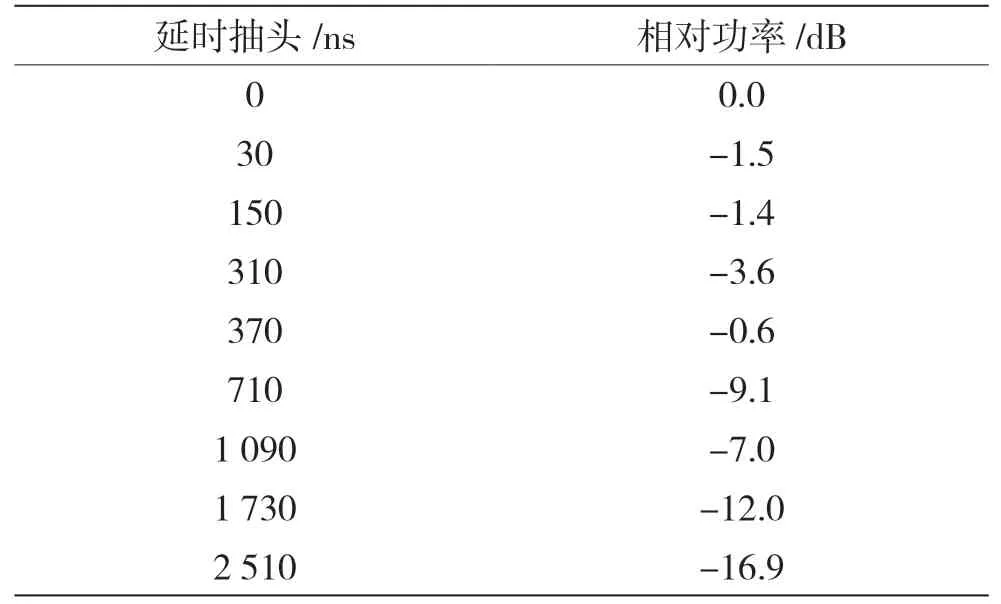
表1 ETU 参数

在ETU 模型下，从-16～0 dB 进行了模拟，记录了定时位置正确的成功率，如图5 所示。

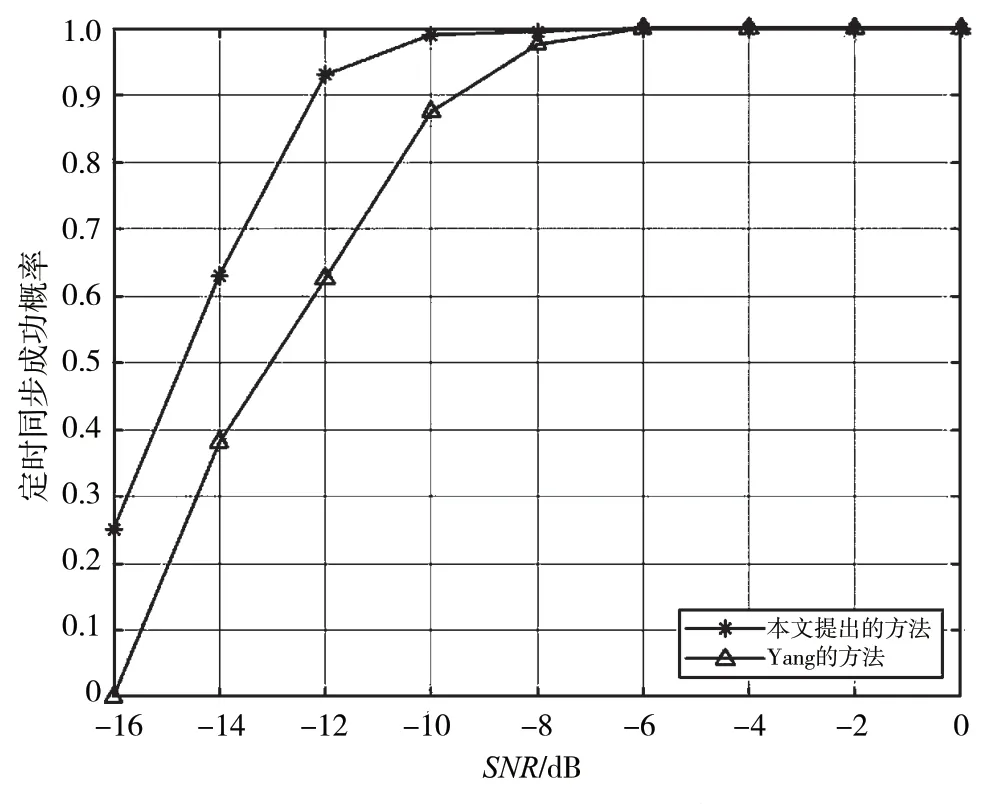
图5 ETU 下的捕获成功率

从图5 中可以看出本文算法在-6 dB 以上情况时的正判率可以达到100%，在-14 dB 时的正判率也可以达到60%以上；但是Yang 的算法在-14 dB时只有不到40%的正判率。

EPA 信道总共有7 条不同参数的路径。参数如表2 所示。

表2 EPA 参数

从-16～0 dB 进行了模拟，记录了定时位置正确的成功率，如图6 所示。

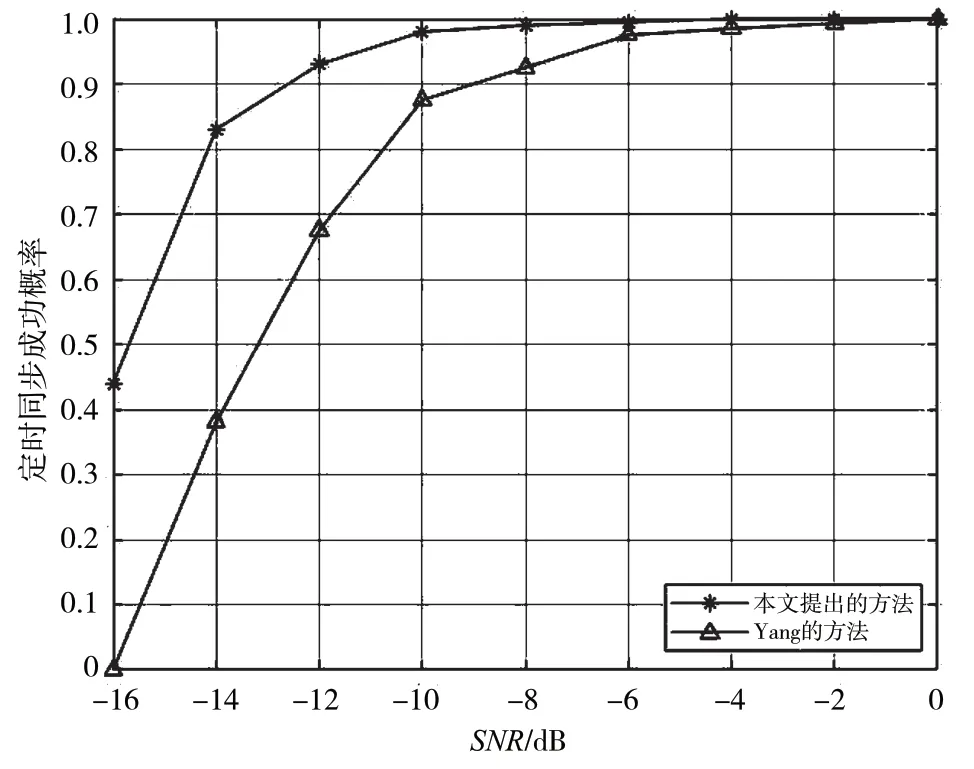
图6 EPA 下的捕获成功率

通过图6 可以看出在EPA 信道中，本文提出的算法在-8 dB 时有97%左右的正判率，在-12 dB以上时有93%左右的正判率；而Yang 算法在-12dB时只有不到70%的正判率。

EVA 信道总共有9 条不同参数的路径，如表3所示。

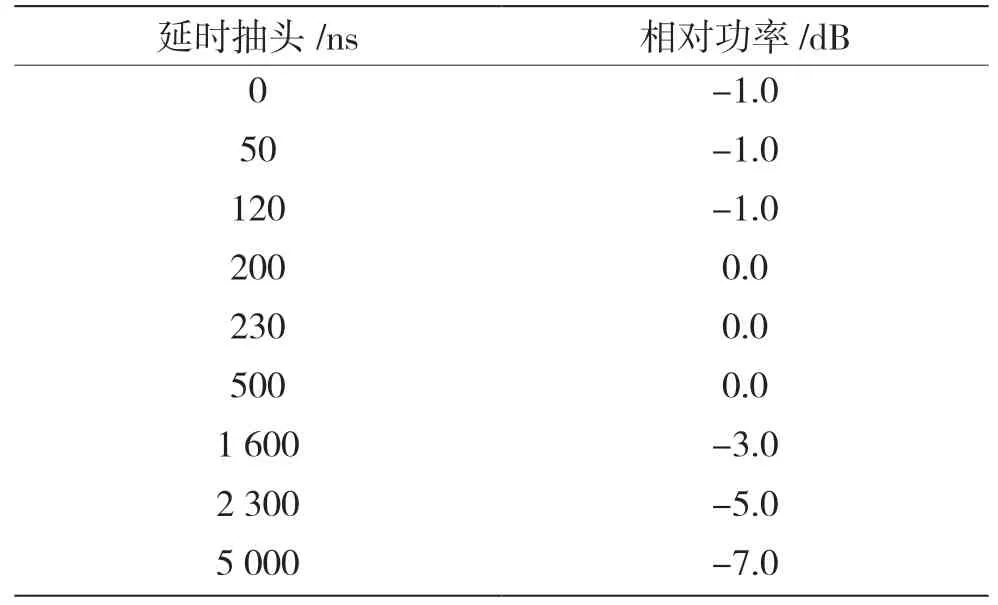
表3 EVA 参数

从-16～0 dB 进行了模拟，记录了定时位置正确的成功率，如图7 所示。

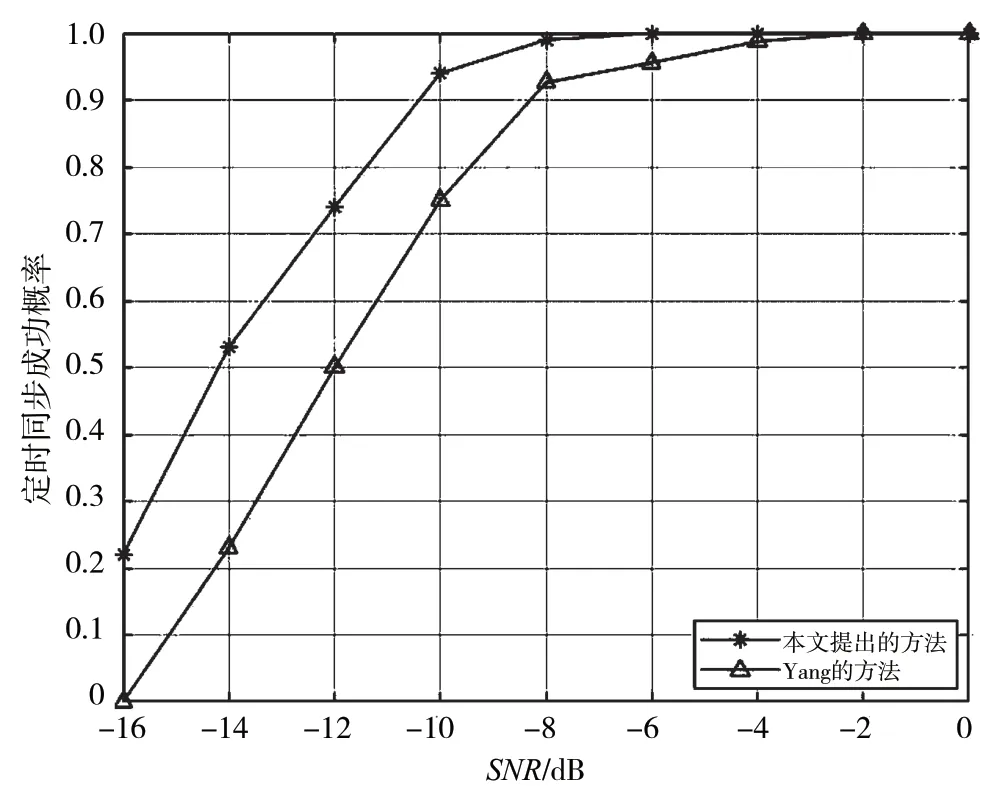
图7 EVA 下的捕获成功率

通过图7 可以看出在EVA 信道中，本文提出的算法在-6 dB 以上时有接近100%的正判率，在-12 dB 以上时有74%左右的正判率。而Yang 算法在-12 dB 时只有50%的正判率。

4 结论

本文利用ZC 序列良好的相关特性，针对多径信道，设计了一种新的训练序列结构和相应的度量函数，并且提出了动态阈值判别方法。通过仿真，验证了该算法在多径衰落信道下，具有良好的定时同步性能。研究表明，该算法为OFDM 定时同步提供了方法借鉴。