基于分布直方图的MFSK 调制识别技术
林秋海,龙 华
(昆明理工大学,云南 昆明 650100)
0 引言
多进制频移键控(M-ary Frequency Shift Keying,MFSK)常用于无线短波信道,是数字通信中重要的调制模式之一[1]。随着信息技术的广泛发展以及对数字通信监听、盲解调的迫切需求,对包含MFSK 在内的数字通信调制模式进行识别,是当前的研究热点[2]。
根据以往调制模式识别的相关研究,技术路线大抵可以分为基于似然比的判决和基于特征提取的统计识别[3]。针对MFSK 的类内识别,比较多的学者使用了基于特征提取的统计识别,如高阶累积量、瞬时频率的统计量等。张文启[4]通过数学推理发现MFSK 的各阶累积量的理论值基本相等,所以先将基带信号微分,再求其4 阶的高阶累积量,以实现2 进制数字频率调制(Binary Frequency Shift Keying,2FSK)、4 进制数字频率调制(4-ary Frequency Shift Keying,4FSK)和8 进制数字频率调制(8-ary Frequency Shift Keying,8FSK)三者的区别;但此种算法计算复杂,且使用高阶累积量需要预估载频才能获取基带信号,而载波预测的准确度对上述特征提取结果影响又较大[5],并不易于实现。陈蕙心[6]考虑多进制瞬时频率个数多于2FSK,故使用一次递归频率均值和2 次递归频率均值来区分2FSK、4FSK 和8FSK;但此方法需在信噪比大于10 dB 以后,才能区分4FSK 和8FSK。谭正骄等[7]使用递归归一化瞬时频率绝对值的均值来区分2FSK 和4FSK,但无法实现8FSK 的区分。王海滨等[8]利用瞬时频率绝对值的标准偏差以实现对2FSK 和4FSK的区分,但也未述及对8FSK 的区分。在时域特征较难以实现MFSK 类内识别的情况下,有学者会考虑使用频域上的特征进行区分,如邓璋等[9]针对信号谱线所在位置的强度设置了一定阈值,而后进行判决,也能实现2FSK 和4FSK 的区分;杜盼盼[10]利用MFSK 基带信号循环谱谱峰的个数也实现了3 类信号的区别,但此类算法都较为复杂。笔者考虑到MFSK瞬时频率的不同,如对瞬时频率进一步统计量分析,在满足区分功能的前提下,能简化算法的复杂度,并进行仿真测试验证该算法的识别准确率。
1 MFSK 的瞬时频率
MFSK 调制方式的本质是利用基带信号去选择载波频率,即利用载波频率的差异来存储基带信息,比如,在2FSK 中,当基带信号为零时,选择一定的载波频率;而当基带信号为1 时,选择的载波频率是在初始载波频率的基础上加上一定的载波偏移。其数学模型为:
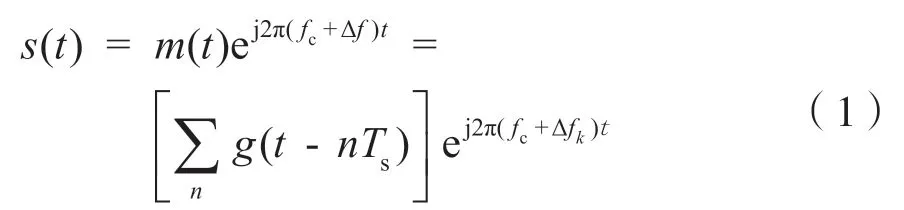
式中:j表示复数;m(t)为基带信号;fc为调制所用的载波信号;Δfk为载波信号频率的偏移量,k值不同时,载波偏移量也就不同;g(t-nTs)为n个脉冲序列,其持续时间都为Ts。
对调制后信号s(t)求取其瞬时相位φ(t)为:
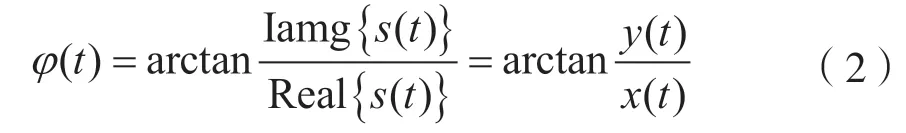
式中:y(t)和x(t)分别为调制后信号的虚部和实部。
因为瞬时相位会受到线性相位分量2πfct的影响,所以在运算过程中会对瞬时相位实施去卷叠,并减去线性分量[11]。则非线性瞬时相位可求解为:
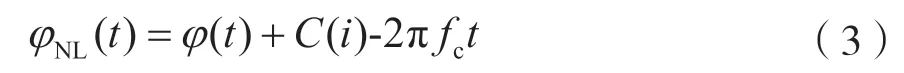
式中:C(i)为实施去卷叠时的补偿因子。
此时,对得到的瞬时相位求取时间差分,就可以得到瞬时频率。计算公式为:

对式(4)进行离散后,可化简为:
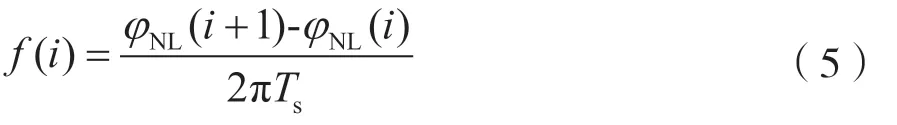
在MFSK 调制信号中,求取的瞬时频率值取决于“M”。即若为2 进制频移键控调制,则瞬时频率应为fc和fc+Δf;若为4 进制频移键控调制,则瞬时频率应为fc、fc+Δf、fc+2Δf和fc+3Δf;若为8 进制频移键控调制,则瞬时频率应为fc、fc+Δf、fc+2Δf、fc+3Δf、fc+4Δf、fc+5Δf、fc+6Δf、fc+7Δf。
2 瞬时频率统计量分析
根据式(5),笔者假设码元数量均为10,信号速率均为200 b/s,载波均为1 200 Hz,采样频率均为9 600 Hz 的2FSK、4FSK 和8FSK 信号3 组。让信号分别经过加性高斯白噪声信道,且信道信噪比设置为5 dB、10 dB、15 dB 3 种情况。通过仿真,得到了如图1、图2、图3 所示的结果。考虑到低噪声情况下,瞬时频率信息容易被噪声淹没,故在求取瞬时频率时,添加了滤波器[12]。
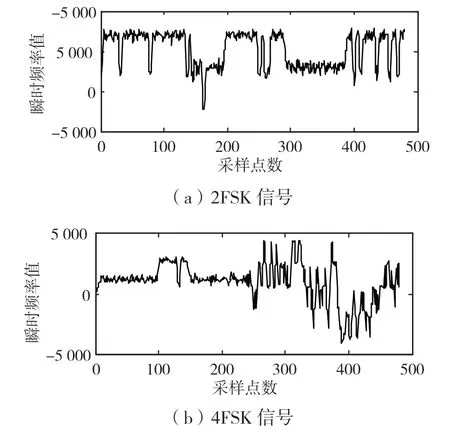
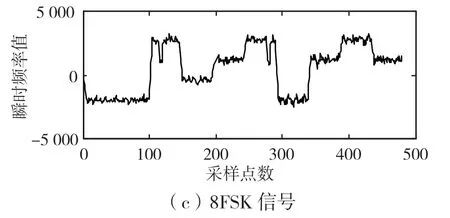
图1 信噪比为5 dB 时,3 种信号的瞬时频率
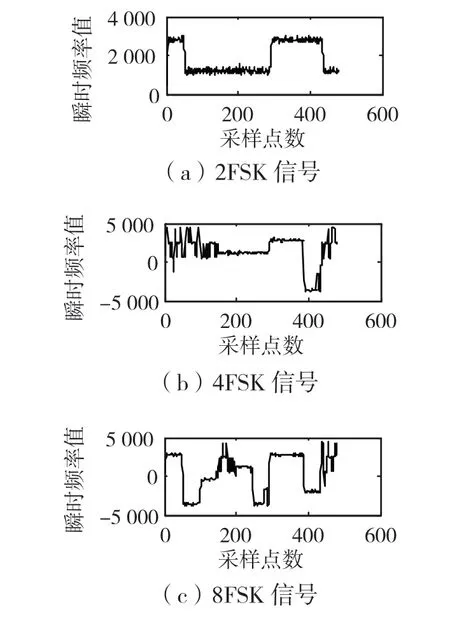
图2 信噪比为10 dB 时,3 种信号的瞬时频率

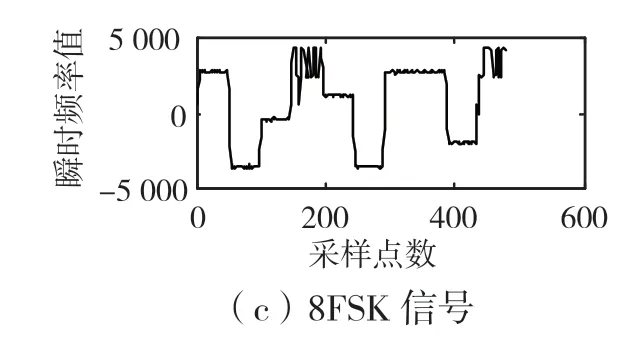
图3 信噪比为15 dB 时,3 种信号的瞬时频率
如图1、图2、图3 所示,2FSK、4FSK 和8FSK 3 个信号在分别经过不同信噪比的高斯白噪声信道后,所得到的瞬时频率具有一定的区别。当信噪比越高时,瞬时频率越能反应出实际码元值。若对取得的瞬时频率进行直方图等统计量运算,理论上可以实现对2FSK、4FSK 和8FSK 3 个信号的区分。
为提高提取统计量特征的鲁棒性,笔者对式(5)求出的瞬时频率进行了去直流和归一化的预处理[13],其数学表达式为:

根据式(5)和式(6),笔者重新假设了码元数量为1 000,信号速率为0.2 Mb/s,使用载波为1 MHz,采样速率为12 MHz 的2 进制、4 进制、8进制频移键控信号,并将信号经过信噪比为15 dB的高斯白噪声信道。考虑码元长度对结果的影响[14],故在此设置的码元长度为1 000。对经过高斯白噪声信道信号进行预处理,并统计其频率直方图后,可以得到如图4 所示的结果。
从图4 可以看出,瞬时频率分布直方图可以较好地反映调制信号调制模式,当分布的波峰有2 个时,可以判断为2FSK 信号;当分布的波峰有4 个时,可以判断为4FSK 信号;当分布的波峰有8 个时,可以判断为8FSK。而且,在截取相同长度信号下,当多进制频率键控分布的瞬时频率值会更多,导致其频率分布的“峰”会更“瘦”,反之更“胖”。
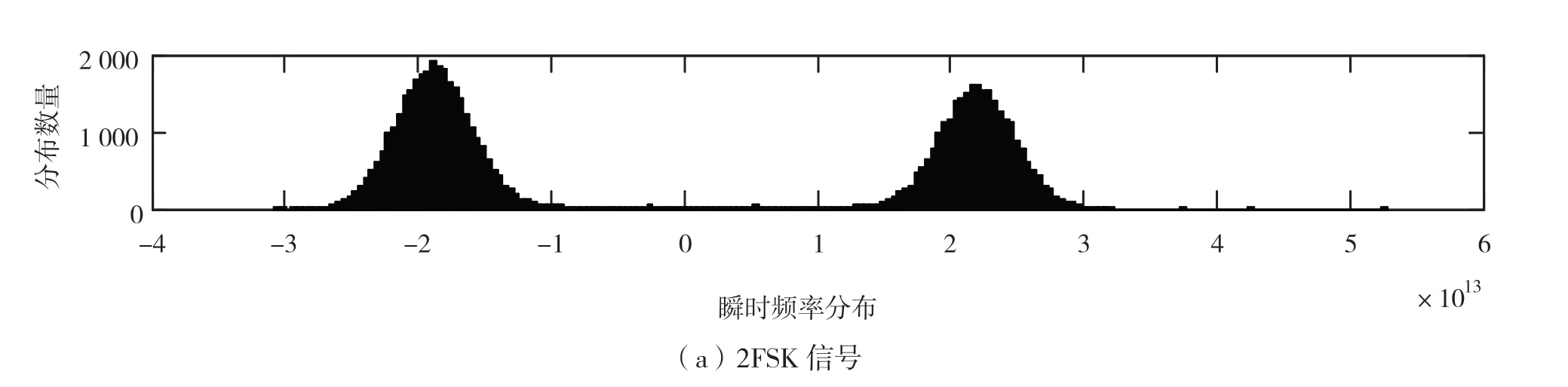
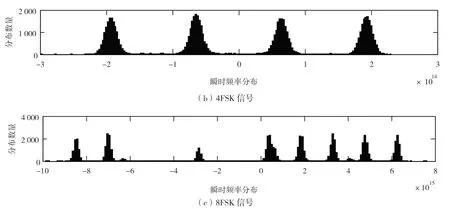
图4 瞬时频率分布
3 基于瞬时频率分布直方图的测试仿真
根据第2 小节的分析,依据波峰数量,可以实现对2FSK、4FSK 和8FSK 3 个信号的区分。在采用决策树判决的情况下,笔者假设了当波峰数量少于3 个时,程序自动判断为2FSK;当波峰数为4个时,程序判断为4FSK;当波峰数超过6 个时,程序判断为8FSK。
为判断笔者所设置门限值的准确度,笔者设计了与第2 小节实验参数一致的实验,即码元数量为1 000,信号速率为0.2 Mb/s,使用载波为1 MHz,采样速率为12 MHz,信道信噪比扩大为1~20 dB。仿真实验共测试500 次,以测算其识别的准确率。同时,笔者以文献[6]的方法作为参考对比,得到如图5 的测试结果。
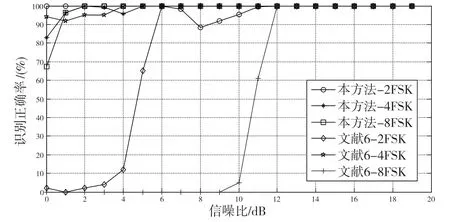
图5 基于瞬时频率分布直方图的测试结果
从图5 可以看出,使用瞬时频率分布直方图来区分2FSK、4FSK 和8FSK 3 个信号,效果要比文献6 中的方法好。使用文献[6]的方法,需要信噪比分别在6 dB、4 dB 和13 dB 时,2FSK、4FSK和8FSK 3 个信号的识别率才能达到100%;但使用本文方法,在极低信噪比(2 dB)的情况下,3 种信号的识别准确率都达到100%。在高斯白噪声信道信道比为1~20 dB 下,3 种信号的平均识别率,本文方法达到98.53%,比文献[6]方法高出26.41%。
4 结语
通过测试仿真发现,MFSK 的瞬时频率直方图具有较为明显的区别,将该特征用在MFSK 的类内识别上,能在低信噪比的情况下较好的实现2FSK、4FSK 和8FSK 3 个信号的区分。在高斯信道信道比为1~20 dB 下,2FSK 的平均识别率为98.81%,4FSK 的平均识别率为98.51%,8FSK 的平均识别率为98.27%,具有较高的理论和应用价值。然而,本文仅使用了一个特征值来区分MFSK 的类内识别,致使2FSK 和4FSK 在部分信噪比的情况下,识别准确率有所下降。下一步,拟参考文献[15]中的方法,将频率分布直方图中波峰距离等因素一并考虑,以增加识别的准确率。

