分组码的几种码限的讨论
冯天树
(北京科技大学天津学院,天津 301830)
0 引言
给定q元信息,位长k,增加m=n-k个监督编码元,编码为n长码n(n>k),构成分组码(n,k,d)或(q,n,k,d)。分组码用符号(q,n,k,d)表示,包括线性分组码和非线性分组码。线性分组码下文中也用符号[q,n,k,d]表示,是群码,有封闭性和包含全0码字。
设C是q元n长码,即C是的子集。d是码C的最小距离,表示为:

式中:d(x,y)表示x和y的汉明距离,即x和y不相同的位数。
如何构造(q,n,k,d)码达到香农极限,一直是信道编码工作者们追求的目标,科学家们在不断地构造出新的好码。在构造新码的过程中,不可不免地遇到一个问题:哪些码可以构造出来,哪些码构造不出来,如果能构造出来,那么该如何构造?现在信道编码理论中出现了分组码的四个限或界(bound):汉明限、Plotkin 限、Singleton 限,Gilbert-Varshamov 限。但所有信道编码教材都对几码限介绍的非常简洁,本文对这四个码限进行详细的讨论和分析,希望对信道编码工作者在构造达到香农极限的新码时有所帮助。
1 几种码限
1.1 汉明限
1.1.1 码限问题
汉明给出了分组码(q,n,k,d)的d的一个上限,这就是汉明限[1]。汉明限为:

说明:
(1)汉明限是必要条件,不是充分的。所有的码必须满足此条件,不满足的这条件的码肯定不存在。
当式(1)取等号时的码叫完备码。令d=2t+1,参数为(n,k,2t+1)的q元完备码满足:
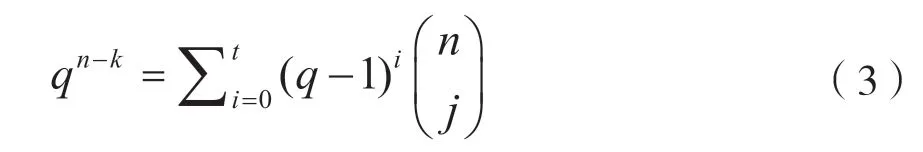
但遗憾的是满足式(3)的q、n、k、d很少。
Golay 求出满足式(3)的参数(q,n,k,d)的只有(2,23,12,7),(2,90,78,5),(3,11,6,5)三组;但Golay 发现二元(90,78,5)不存在[2],只存在二元(23,12,7)码和三元(11,6,5)码。二元Golay (23,12,7)码满足:
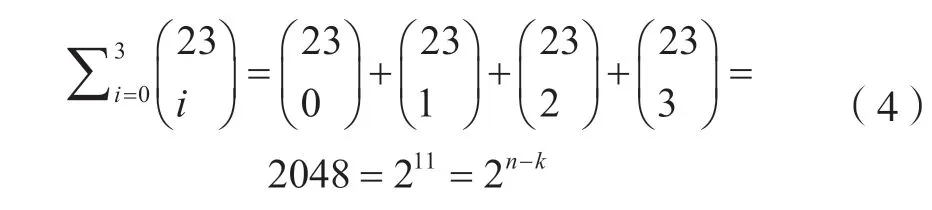
完备的线性分组码只有以上几种,后来数学家们找到一些非线性的q元完备码[2]。
(2)q元(n,n,1)码是完备码,但毫无纠错能力,没增加任何校验位。
(3)二元码(2t+1,1,2t+1)奇数长的重复码,是完备码,许用码组只有两个码:全1 码、全0 码。
(4)q元汉明码的码距d=3,是码。q=2 时,为(2m-1,2m-1-m,3),m=n-k是监督位个数。
(5)并不是任意给定q、n、k、d,都能构造出相应的(q,n,k,d)码,使q、n、k、d满足式(2)的约束。
对达不到汉明限的非完备码,有个覆盖半径问题。
1.1.2 覆盖半径问题
[定义1]覆盖半径:码集合C(许用码组)是的子集,以每一个属于C的码v为球心,以ρ为半径的球,对许用码组的所有码字做这样的球,让这些球并集等于。最小的ρ称为码C的覆盖半径,记为t(C)。
线性分组码的t(C)实际上是编码矩阵陪集首(或译码校验子)的最大汉明重量[1],即:
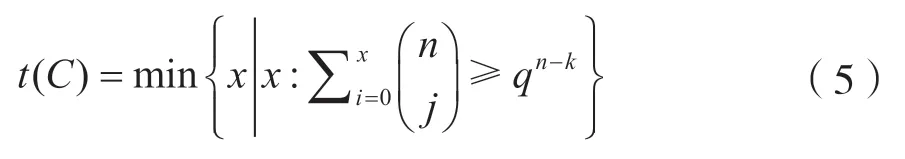
[定义2]每一个属于C的码v为球心,以ρ为半径的球,所有球不相交的半径ρ的最大值叫码C的球半径,记为S(C)。
显然有:
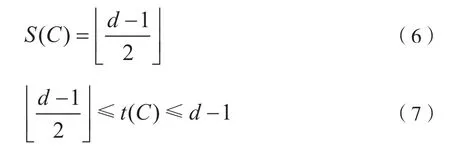
如果t(C)=S(C),式(2)取等号,码C就是完备码。例如,汉明码C的=1=S(C),二元Golay 码(23,12,7)的=3=S(C)。
对非完备分组码C求覆盖半径t(C),是一非常难的问题,数学家们一直在探索[3-4],覆盖半径t(C)和相应的码的码重分布没有对应关系,虽然线性码的最小码重等于最小码距。
t(C)越小,空间中包含的许用码组的码字越多,越接近完备码,因而t(C)越小的码越好。但如何构造小t(C)的码,人类仍然未知。
1.2 Plotkin 限
1.2.1 码 限
Plotkin 也给出了线性分组码[q,n,k,d]的d的一个上限,被称为Plotkin 限[5],码限为:
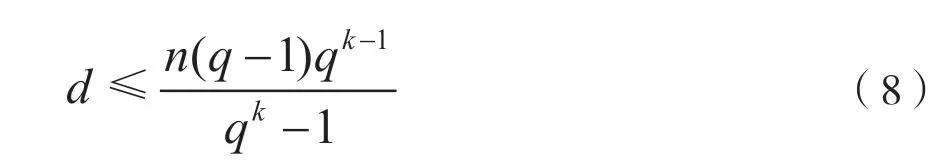
Plotkin 是根据同一[n,k]线性分组码,有qk(n-k)个不同的生成矩阵;每个矩阵产生的许用码组的总重量相同,为n(q-1)qk-1;每码的非零最小码重(最小码距)不会大于平均码重:。
对非线性分组码(q,n,k,d),M是码字总数(对应线性码的qk),有如下结论:

证明思路是分组码的总距离小于等于nM2(q-1)/q,再除以总码子对M(M-1)。
式(8)的条件也是[q,n,k,d]码存在的必要条件,分组码必须满足此条件。
1.2.2 等重码
[定义3]等重码:式(8)取等号时的码叫等重码或单纯码(simplex code),这时码组的所有非零码的码重一样。
线性等重码的性质如下:
(1)可以证明[6]:q元等重线性码[q,n,k,d]是q元汉明码的对偶码,对汉明码m=n-k是监督位长度,对等重码m是信息位长度。
(2)当q=2时,二进制线性等重码[2m-1,m,2m-1],码 长n为2m-1,信息位数为m,校验位数2m-1-m,许用码组个数为2m,每个非零码字的重量(码距)是,例如,[3,2,2]、[7,3,4]、[15,4,8]码等等。
(3)以等重码所有许用码为行构成码矩阵,码矩阵的列数比行数多一,即是(2m-1)×2m矩阵。
(4)因为等重码的码矩阵的列互换,码的重量不变,那么码矩阵列互换不影响码重或码距,生成矩阵列互换即可得到。
1.2.3 二元码线性等重码的构造方法
(1)方法1
先构造汉明码,再用汉明码的H矩阵做G矩阵即可生成等重码。m(信息位个数)位二元共2m个组合,去除全0 码,剩下的2m-1 列构成的矩阵就是等重码的生成矩阵。
也可用循环码生成,xn-1=g(x)h(x),单纯码的生成多项式是其对偶汉明循环码的h(x)。
(2)方法2
将2m×2m阶0,1 Walsh-Hardamark 矩阵(即 将普通±1 的Walsh-Hardamark 矩阵的1 变为0、-1变为1),去掉全0 列,得到(2m-1)×2m矩阵即为许用码矩阵[7]。
非线性等重分组码这里不做讨论。
1.3 Singleton 限
1.3.1 码限
设Aq(n,d)表示长为n最小码距为d的q元分组码所能容纳的码字个数的最大值,即Aq(n,d)=max{M|存在分组码(n,m,d),给定n,d}。
Singleton给出了分组码(n,k,d)的Aq(n,d)的上限:

当分组码为线性码[n,k,d]时,d的上限为:

这时码限与q无关。
式(10)和式(11)表示的极限叫Singleton 限。对线性分组码,Singleton 的证明思路是:对线性分组码,最小码距是最小的非0 码重,此时信息位不可能全0,至少一个1,而n-k位监督信息最多有n-k个1,所以最小的非0 码重至少为n-k+1。
1.3.2 MDS 码
[定义4]使式(11)等号成立的码叫极大距离可分(Maximum Distance Separable,MDS)码,此时达到Singleton 限.
对二进制线性分组码,只有重复码(n,1,n)奇偶校验码(n,n-1,2)及(n,n,1)码,这三类码是MDS 码,叫平凡MDS 码。2 ≤k≤n-2 的(n,k,d)MDS 码叫非平凡MDS 码。
对二进制线性码,MDS 码都是平凡MDS 码,没有非平凡的MDS码。因为q=2时n=3,(3,1,3),(3,2,2)码都是平凡码。
著名的里德-所罗门(Reed-Solomon,RS)码q=2,n=q-1=2m-1 是非平凡多进制MDS 码。
线性[n,k,n-k+1]MDS 码的对偶码是[n,n-k,k+1]码,也是MDS 码。
1.3.3 MDS 码的猜想
设M(k,d)=max{n|存在(q,n,k,n-k+1)码}
[命题1]如果q≤k,那么M(k,d)=k+1
q元分组MDS 码猜想[8]为:

对线性码,设m(k,d)=max{n|存在线性码(q,n,k,n-k+1)}

这猜想至今没被完整证明,只部分被证明,n、k、d是小数字时可以验证。
1.3.4 多项式码
[定义5]多项式码:设a1,a2,…,an是Fq中n个不同的元素(n≤q)(1 ≤k≤n),则集合:
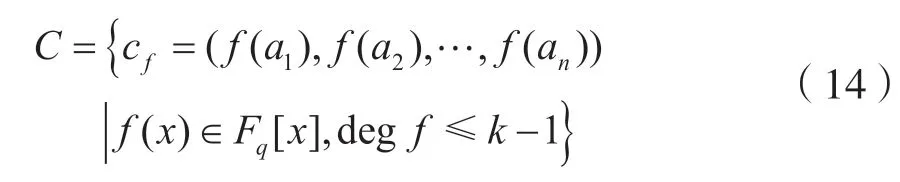
是q元[n,k,d]线性MDS 码。
可以证明多项式码的d=n-k+1,只要多项式的次数小于等于k-1,n≤q,则可构造一大类MDS 码。扩展RS 码是f(x)取固定某函数的特殊多项式码,多项式码提供了一大类构造MDS 码的方法。
1.4 Gilbert-Varshamov 限
1.4.1 码 限
Gilbert 用代数的方法证明分组码(n,M,d)(不一定线性),如果存在下关系:
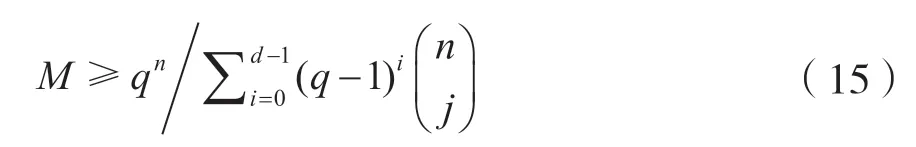
那么这样的(n,M,d)分组码一定存在。
如果线性分组码[q,n,k,d]存在以下关系:
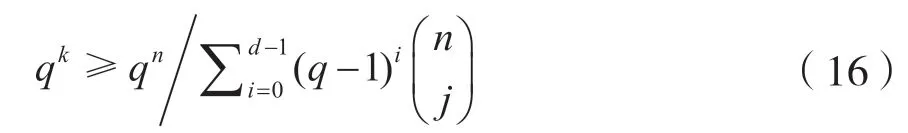
或者是:
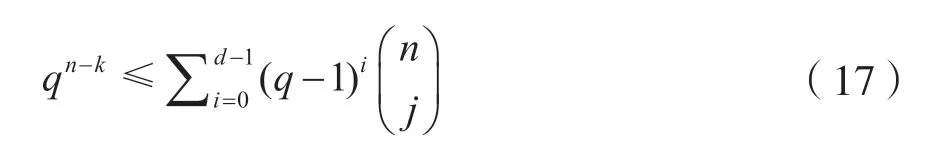
那么这样的线性[n,k,d]码一定存在,这就是Gilbert 限,该条件是码存在的充分条件,不是必要的。
Gilbert 的证明思路:以许用码的每码字为中心,以d-1 为半径的汉明球的并的集合个数,肯定超过的元素个数。
Varshamov 用概率统计的对线性分组码方法证明了:
设q≥2,对每个,且0<ε≤1-Hq(δ),那么一定存在(n,k,d)码

式中:R=k/n,δ=d/n,Hq(δ)是q元熵函数:
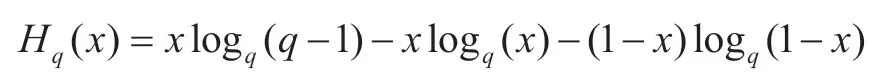
可以证明式(16)当n→∞时和(18)是一样的,都称Gilbert-Varshamov(GV)限。
式(16)叫非渐进GV 限,式(18)叫渐进GV 限。
1.4.2 码限说明
式(16)这个限很松,给定n和k,d存在下限,或给定n和k,d存在下限。当n、k、d、q是小数字时,汉明码、等重码、RS 都比非渐近GV 限好;但比式(16)下限小的码,是存在的。
[命题2]更紧的非渐进GV 限是:
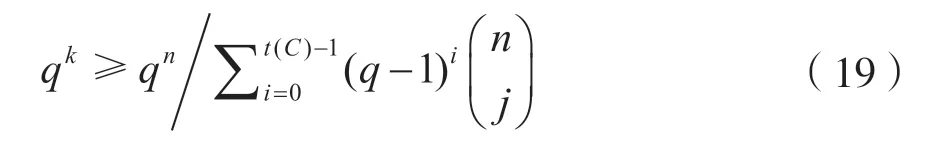
t(C)码C的覆盖半径,所以求码的覆盖半径很重要。证明略。
[命题3]对任意(n,k)线性分组码,总存在d=1的码。
证明:当生成矩阵的第k行为n长(0,0,…,0,1)或第k行有奇数个1 时,当发送信息为k长的(0,0,…,0,1)时,码字为n长(0,0,…,0,1),最小非0码重为1,所以d=1。
[命题4]式(16)的等号,不可能存立,除非d=1。
证明:因为取等号时,以码为球心以d-1 为半径的球,会两不相交,并覆盖整个空间。这等效于:完备码的以码为球心以(d-1)/2 为半径的球覆盖整个空间,(d-1)/2=d-1,所以d=1。证毕。
2 4 种码限的比较和说明
如图1 所示是q=2 时的几种限。
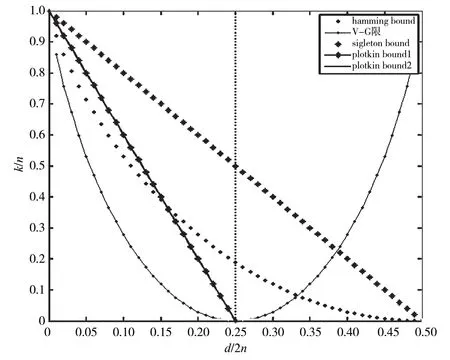
图1 二进制码限
图1 中Plotkin bound2 曲线是:
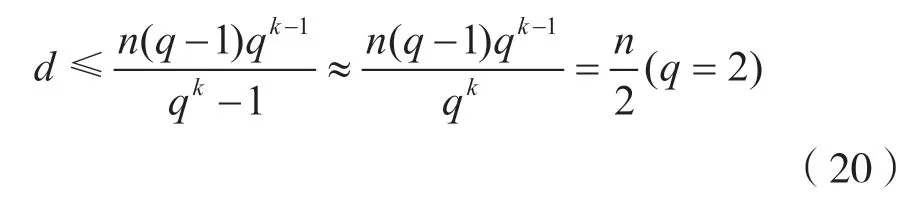
2.1 对几种码限的比较说明
2.1.1 说明一
在几种上限(Plotkin、汉明、Singleton)中,任意一码,只能满足3个限中最小的。图1中,R<0.4时,码限应小于Plotkin 限;R>0.4 时,码限应小于汉明限。意味着:想构造完备码,R必须是大于0.4高码率码;想构造等重码,必须R小于0.4。
例如:
二进制汉明码(15,11,3) 码,其Plotkin 限为dplotkin=7,其Singleton 限为dsingleton=4。
真实d=3 <dplotkin,d<dsingleton。
二进制等重码(15,4,8) 码,其汉明限为dhamming=7,其Singleton 限为dsingleton=15-4+1=12。
因为,215-4>C(15,0)+C(15,1)+C(15,2)+C(15,3)
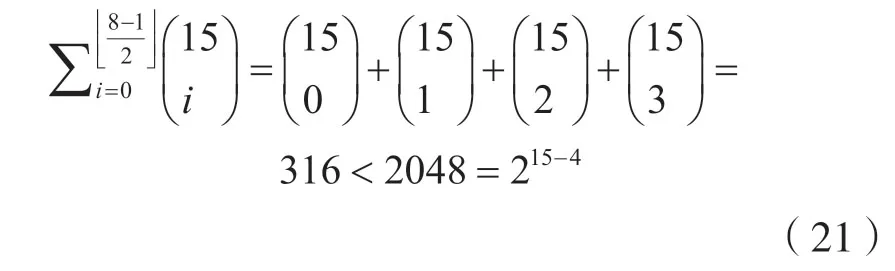
等重码也是满足汉明限。
二进制等重码(15,4,8)码在GV 限曲线的上面,则:
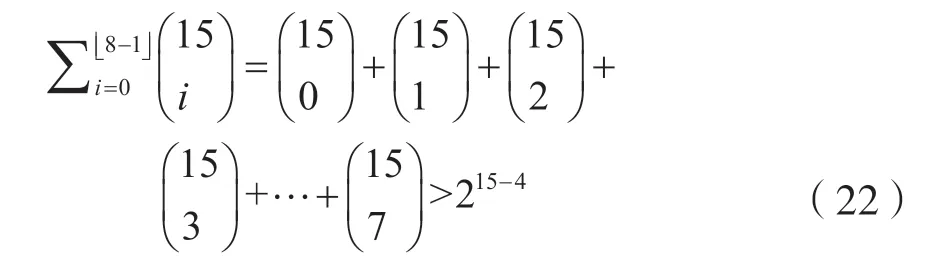
2.1.2 说明二
GV 限条件是充分条件不是必要的,分组码可以位于GV限曲线的下面,并不是所有的码都满足GV限。
例如(15,4,5)码:
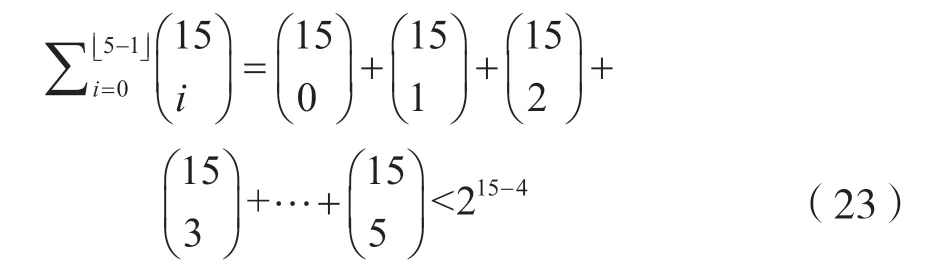
但该码存在。
2.1.3 说明三
表1 是n=16 的所有k的二进制循环码及其最小d。
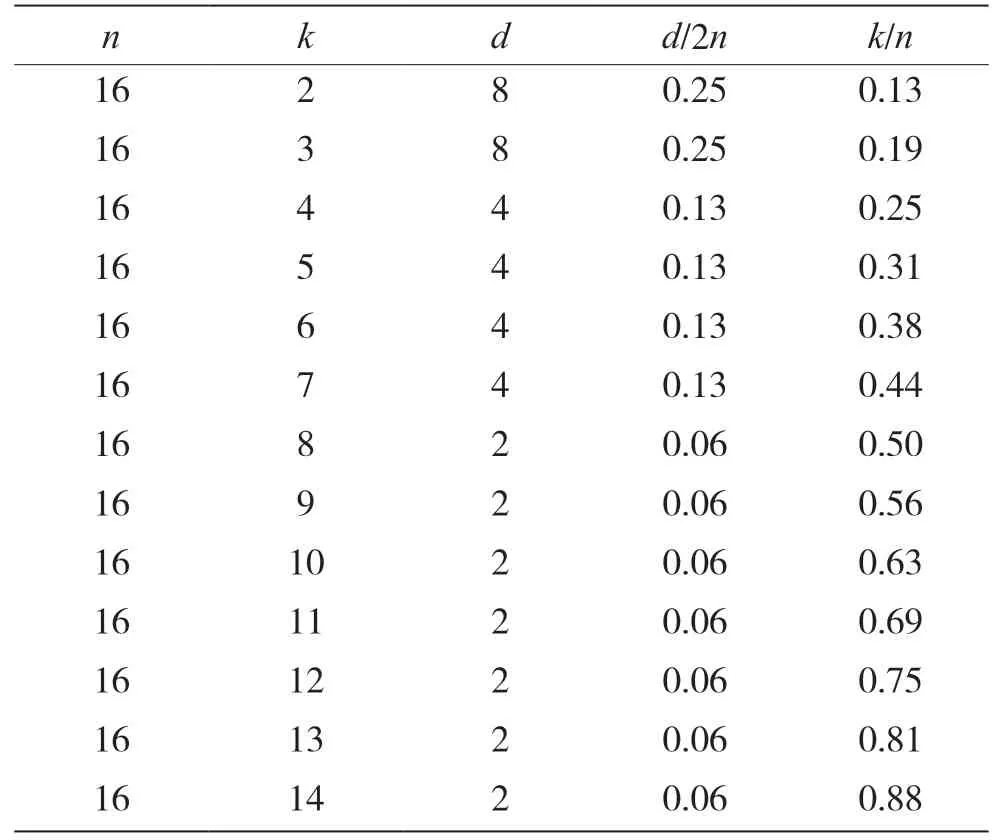
表1 n=16 的所有k 的二进制循环码及其最小d 的码限
图2 是n=16 的所有k的二进制循环码在码限图上的情况(小圆圈)。
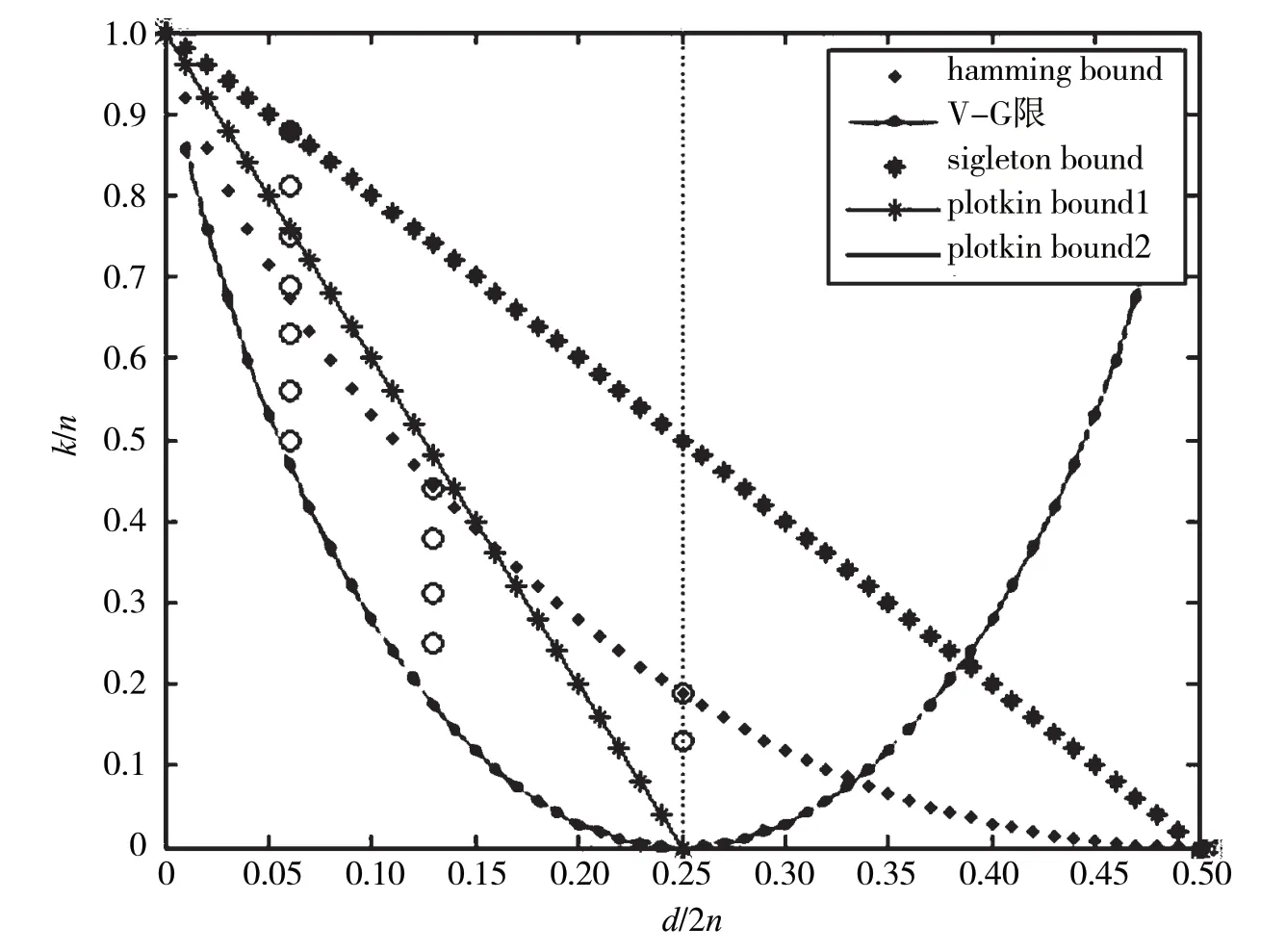
图2 n=16 的所有k 的二进制循环码及其最小d 的码限
2.2 关于Singleton 限图的一个问题的解释
在图1 的码限图中,Singleton 限曲线在汉明限曲线和Plotkin 限曲线的上面,而汉明限Plotkin 限是必要条件。让人感到奇怪的是:达到Singleton 限的MDS 码,怎么会满足汉明限和Plotkin 限呢?下面举例说明。
例如:RS 码(7,2,3)(t=1,q=8)满足汉明限。满足Plotkin 限。
这是因为图1 画的二进制码限图,满足Singleton 限的MDS 码应是q进制码(不是二进制),且必须满足q>n,而把Singleton 限画在二进制码限图上(某些文献也这样画Singleton 限曲线),就会产生误解。
3 码限对香农信道编码定理的意义
香农给出了著名的信道编码定理:在存在差错概率的信道上,如果传送码率不超过信道容量C,那么一定存在一种纠错编码的方法,使接收端能够无误码接收。香农信道定理的证明的方法是:随机码、码长n无穷长和最大似然译码。
香农在信道编码定理中使用随机码和n→∞时,当R=k/n<信道容量C,那么平均误码率将趋近0。R<C;但R不能趋近0,R越接近C,码越好。
从上文中的几个码限可以得出,为达到香农限,不可能无限增加d,因为d的增大是受码限约束的,并且d的增大对Pe的减少是有限的,为达到香农限只能想别的办法。
[定义6]q≥2,设有一组{ni}i≥1,是一组递增的分组码长度,假设存在序列{ki}i≥1和{di}i≥1,使得存在q元分组码Ci=(ni,ki,di),那么码序列Ci={Ci}i≥1是码序列。C的码率定义为:对汉明码CH∶ni=2i-1,ki=2i-1-i,di=3,R(CH)=1,δ(CH)=0。

而构造香农码要求:R<信道容量C,要Pe→0,δ不能→0,否则没纠错能力。R不能→0,否则Pe→0 的代价不是在R略小于容量C时得到的。显然汉明码不能满足香农定理的要求。
同样,等重码簇的R=0,δ=0.5,RS 码簇、MDS 码簇都不能满足n→∞时,R和δ能同时保持大于0,不趋近0。
渐进GV 限,如式(18),对构造香农码的意义:是否存在能用代数方法规则构造出来的码,n→∞时R和δ能同时保持大于0,不趋近0。
所以数学家们在构造n→∞时R、δ都不趋近0 的码。1972 年Justesen 构造出这种码,但离渐进GV 限有点距离。
现在数学家们把码空间的码解释为代数几何中的影射空间的曲线,在构造渐进GV 码如仙农码方面有一定的进展[9]。
4 结语
本文对信道编码中的分组码的汉明限、Plotkin限、Singleton 限、Gilbert_Varshamov 限四种距离限进行了讨论和分析,说明达到这些限时的码的性质和码的构造方法,并对这些码限进行了比较和分析。结果说明:要降低误码率到达香农限,增加码距的作用对是有限的,关键还是靠增加码长和构造新的编译码方法。这些码限特别是GV 限对构造香农理想码有重要意义。这种思路和工程界构造的Turbo码、LDPC 码和polar 码,不是一条思路。另外,分组码还有Johnson限、Griesmer限、Elias-Bassalygo限,本文未做讨论。

