一种对无人机通信链路中扩频信号识别改进方法
涂 航,熊 刚
(1.海军参谋部,北京 100841;2.中国电子科技集团公司第三十研究所,四川 成都 610041)
0 引言
随着智能化新技术的发展,无人机在民用和军事领域中具有广阔的应用前景。无人机通信链路包括下行的图传与上行的遥控链路,是无人机实现测控信息传输的重要通道。地面控制站相当于无人机系统运行的核心大脑,而无人机遥控链路发挥着关键的控制指令发送作用[1]。无人机通信链路示意图如图1 所示。
图1 无人机通信链路
无人机通信链路信号样式有正交相移键控(Quadrature Phase Shift Keying,QPSK)调制信号、16 正交幅度调制(Quadrature Amplitude Modulation,QAM)信号等。近年来,因为扩频信号具有抗多径性能良好、传输速率高、抗截获等特点,已经成为了无人机遥控链路的一种重要信号样式[2]。全球无人机市场占有率最高的大疆系列消费级无人机大量采用了直接序列扩频(Direct Sequence Spread Spectrum,DSSS)信号作为其通信方式;军用无人机如外军的通用数据链(Common Data Link,CDL)、战术通用数据链(Tactical Common Data Link,TCDL)等也选取了DSSS 扩频信号方式,可为系统提供较强的抗截获性能。
由于扩频信号对于无人机通信的重要性,与之相应的信号识别技术成为了监测和对抗领域重要研究课题。在当前日益复杂的电磁环境里,信号纷繁,种类较多,扩频信号识别是后续还原无人机遥控链路传输信息的前提[3]。然而,一方面,在非合作情况下可得的目标先验信息较少,属于盲处理范畴;另一方面,扩频信号有时湮没在背景噪声里,为信号识别带来了挑战。传统的信号处理方法对DSSS 扩频信号的分析识别并不太理想[4],因此引起了许多学者和研究机构的关注。文献[5]分析了根据时域能量识别扩频信号的方法;但是需在较高的信噪比条件下才能使用,对于功率微弱的DSSS 扩频信号处理效果并不是很理想[5]。文献[6]中描述了一种基于频域谱分析的识别思路,该方法对信号频谱估计的要求较精准,否则提取的频域特征不稳定,在实际的复杂电磁环境中难于识别扩频信号[6]。文献[7]的方法是通过对信号六阶矩的特征计算判别扩频信号,并区分出其与QAM 信号和相移键控(Phase-Shift Keying,PSK)信号,不需要很高的信噪比条件;但该思路的运算量大,处理资源开销多,不利于实际中快速识别应用[7],还须采用新的算法思路。
针对上述问题,本文提出一种无人机通信链路中扩频信号识别改进方法。该方法首先通过可调节步长的自适应滤波实现对复杂干扰的抑制,其次结合对扩频信号的多重相关累积特征的提取分析,最后以期得到更好的识别效果。
1 扩频信号分析原理模型
无人机在空中飞行进行通信时,遥控链路中DSSS 扩频信号的信噪较低,需要从实际的强噪声背景中判断出信号是否存在,并对信号的载频、带宽等参数进行估计,然后经过下变频和滤波抽取等处理,得到基带信号。DSSS 扩频通信收发传输原理模型如图2 所示。
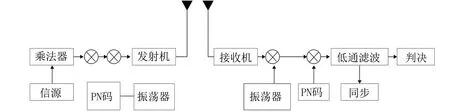
图2 扩频DSSS 通信收发传输原理模型
DSSS 信号的数学模型可表示为:

且有:
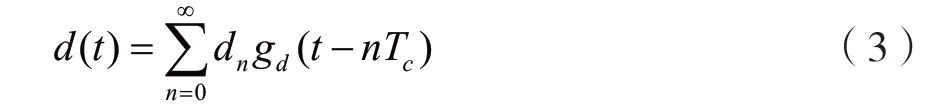
式中:p表示扩频信号的功率;d(t)表示扩频码序列;Tc为信息码周期;fc表示载波频率;θ表示信号相位,初相位通常为0;t表示时间;下标c表示载波;下标d表示延时;g(t)表示码元脉冲成型函数;dn表示原始信息码。
在参数估计的过程中,可先用改进的Welch 谱估计思路进行频率的粗估计,通过对信号序列数据分段,计算每段的周期图,然后进行平均以获得估计值。相对于根据单个周期图的估计,此方法可减小估计值的方差。在初步的频率分析估算后,还可采用四次方谱算法开展对频率的精估计,对于DSSS 扩频信号、二进制相移键控(Binary Phase Shift Keying,BPSK)调制和QPSK 调制信号,都能得到估计结果。可由式(4)计算出频率fc精确估值(fc)fine为:
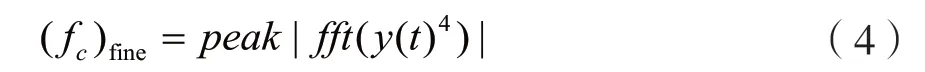
式中:peak(·)表示取峰值;fft表示对信号进行傅里叶变换;y表示DSSS 信号量。
此外,还可估计出其他参数,包括符号周期、定时偏移等,对于扩频信号还可以进一步估计扩频码序列从而解扩,最后可对信号解调进行信息恢复。
扩频码具有周期性,并且信号扩频码序列的统计特性与白噪声近似,所以相关值也会呈现明显的周期性峰值,而对于常规的调制信号,仅可能在相关域平面的中心位置处出现最高峰,且其相关峰不会有周期性,因此根据扩频相关性质能够对信号进行识别。DSSS 信号相关峰计算原理模型如图3 所示。
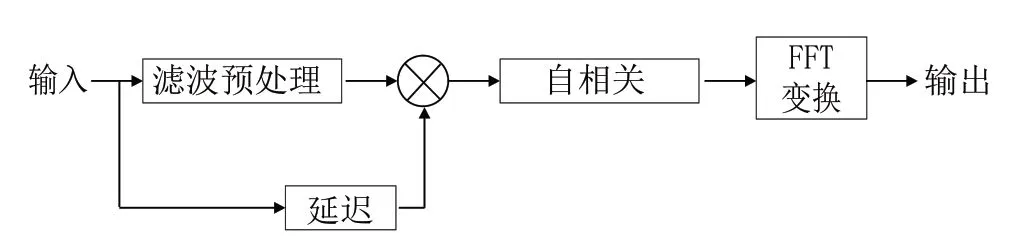
图3 扩频信号相关运算模型
扩频信号延迟相关谱可根据图3 模型得到。延迟相乘信号r(t)的表达式为:

式中:τ表示延迟量。
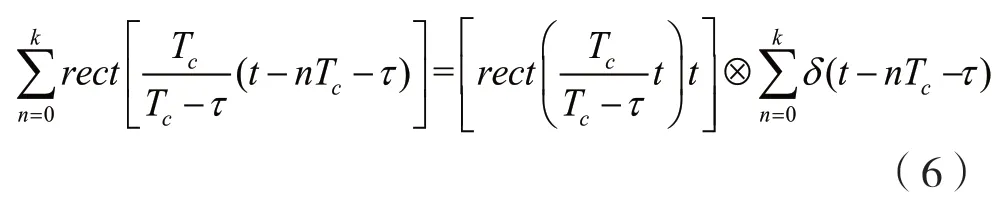
式中:δ(t)表示脉冲冲激响应函数。
然后进行FFT 变换得到信号相关谱,并可从中产生的谱线为:
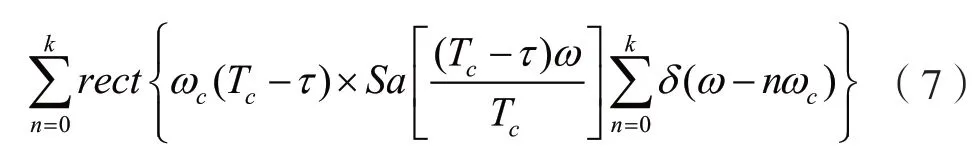
根据式(7),在码速率n倍位置处存在相关谱的谱线,在对无人机通信链路中扩频信号识别时可以利用此特征。考虑到无人机采取了宽带通信传输方式,在信号处理实际应用中需要满足过采样条件,Rc为扩频码速率,则采样率fs应取:fs≥10Rc。设信号y(t)经过模数转换ADC 采样离散化后为y(n),可得无人机扩频信号相关谱的连续部分为:
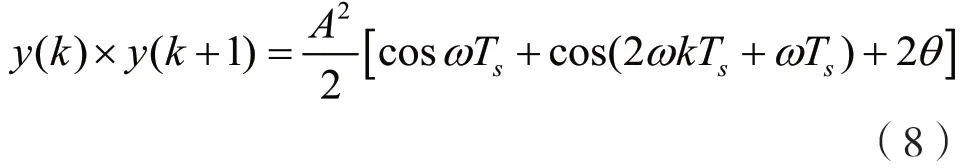
式(8)中含有多个基于扩频码速率的谱线,从而可针对性地进行有效搜索判识。
2 新改进识别算法分析
为了消除在无人机信号识别中干扰及噪声的影响,需要对信号进行滤波。面临复杂的电磁环境中存在的许多较大的背景干扰,可采取基于自适应滤波的处理思路[8]。自适应滤波算法中应用较广泛的是最小均方误差(Least Mean Square,LMS)算法,可在信噪比相对较低情况下抑制干扰,结构易于实现[9];但传统思路因为采取恒定的步长因子,导致收敛速度慢,稳定性较差[10]。本文在此处引入一种可调节步长的改进LMS 方法,可提高收敛速度,并使误差得到优化,增强了对干扰噪声的抑制效果,鲁棒性强。对于待处理的信号s(t)的表达式为:
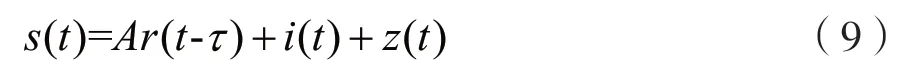
式中:A表示幅度因子,A=1;r(t)表示延迟相关信号,τ=0 时延迟为0;i(t)表示干扰分量;z(t)表示噪声分量。式(9)的归一化离散采样形式为:
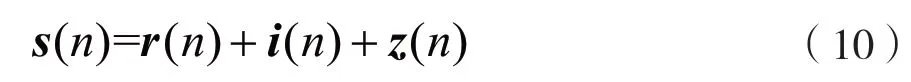
式中:s(n)、r(n)、i(n)、z(n)是相互独立的序列。
s(n)还可用线性回归模型进行表示,即为:
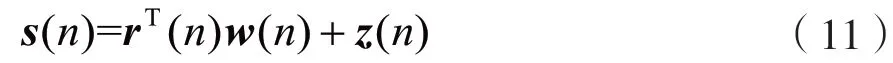
式中:z(n)为高斯噪声,均值为0,均方差为;w(n)为权系数向量。设权向量值的偏差为v(n),e(n)为系统误差,v(n)与r(n)独立,基本的自适应滤波权向量更新表达式为:
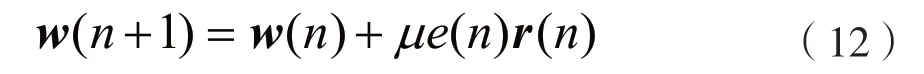
式中:μ表示步长因子。
设r(n)的维数为M,峰度因数为k,即自适应滤波器的阶数。权值偏差的更新表达式为:
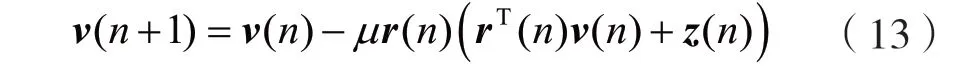
设为r(n)的均方差,通常μ值一般较小,有:(M+k-1)<<2
在实际中k>1,可得:
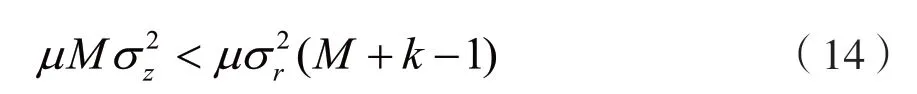
从而得出步长因子最大取值有:
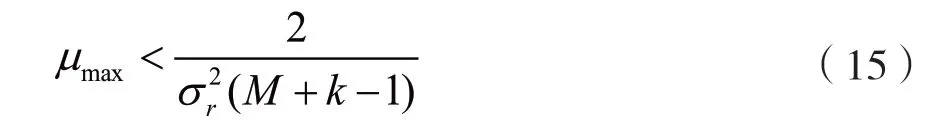
在可调节步长的思路中,可采用最小相关谱能量误差形式实现步长因子的更新,并逼近达到理想步长的调整匹配目标。设初始步长因子为μ0,改进算法中初始的变步长因子应大于传统LMS 算法,使得算法收敛速度快。在干扰信号的滤除过程中,变步长因子迅速达到稳定值。合理的步长取值范围应为μmin~μmax,其中误差最小变化量Δe(n)min为:

在自适应滤波过程中,对权系数向量首先进行初始化设置。设权向量的维数为M,误差信号e(k)的频域变换为E(k),sign(·)表示取符号函数,Var(·)表示取方差函数,L表示输入数据块长度。变步长因子的计算表达式为:
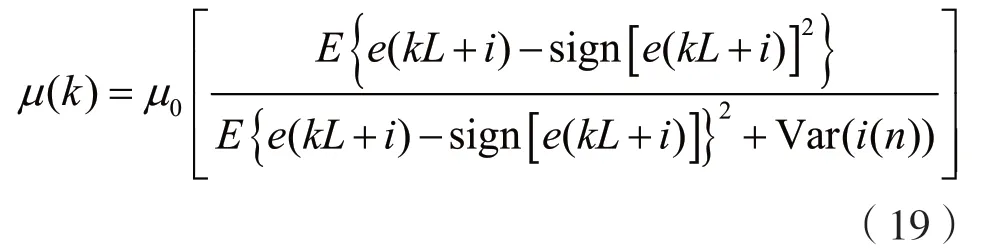
对于相关谱进行最小均方误差LMS 计算,进行权向量的更新,反复迭代,直至实现完全消除干扰。
可调节步长的LMS 方法在不同输入信噪比下的信噪比优化因子如表1 所示。

表1 LMS 算法在各输入信噪比下的优化因子
下面分析基于多重相关累积的思路,进一步降低通信链路环境中的噪声影响,取得更好的抗噪效果。该方法充分拓展了传统思路,得到更强的相关性能,抑制干扰信号,有利于从复杂背景中识别出微弱信号,使得算法提取出的特征更稳健。本文改进的多重相关累积算法结构如图4 所示。
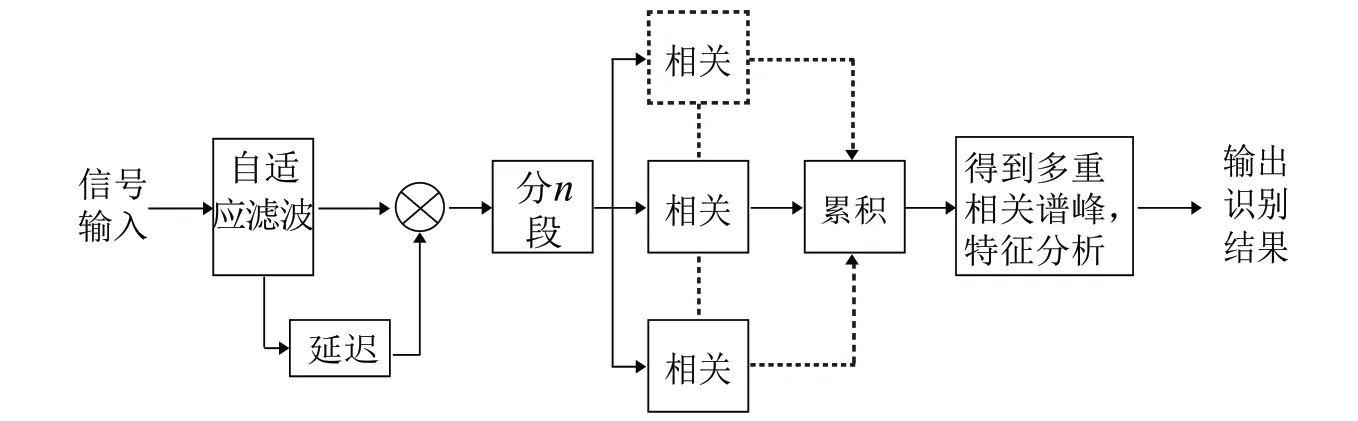
图4 改进的多重相关累积算法结构
信号的相关谱函数分析式为:
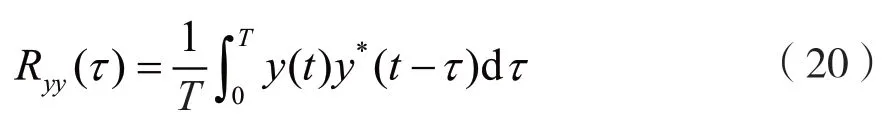
设加窗长度为M,则相关谱累积函数的二阶矩为:

并可得:
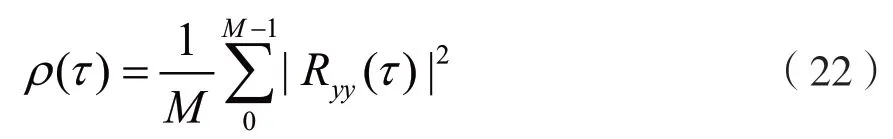
对加窗处理后的信号求取均值平滑,再对扩频信号相关谱的谱线变化进行分析,谱线之间的间隔是相同的,且都出现扩频码速率的倍数周期位置。当存在多个信号的情况时,DSSS 信号的相关峰能量将和其它信号的叠加,导致在相关结果图的中心位置的幅度达到最大,这主要是由其它类型调制信号性质造成的,DSSS 信号在该位置的相关峰幅值小于QPSK 信号和16-QAM 信号,但DSSS 信号存在非中心位置处周期性的相关谱线,QPSK 信号、16-QAM 信号却不具有。多信号情况时的相关谱峰如图5 所示。
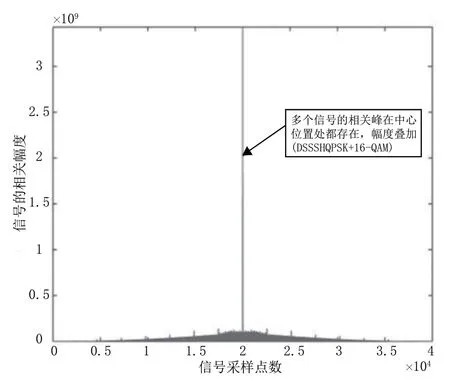
图5 信号多重相关峰(DSSS+QPSK+16QAM)
对中心位置相关峰幅度减小,并放大非中心位置处的信号各相关峰谱线,如图6 所示。
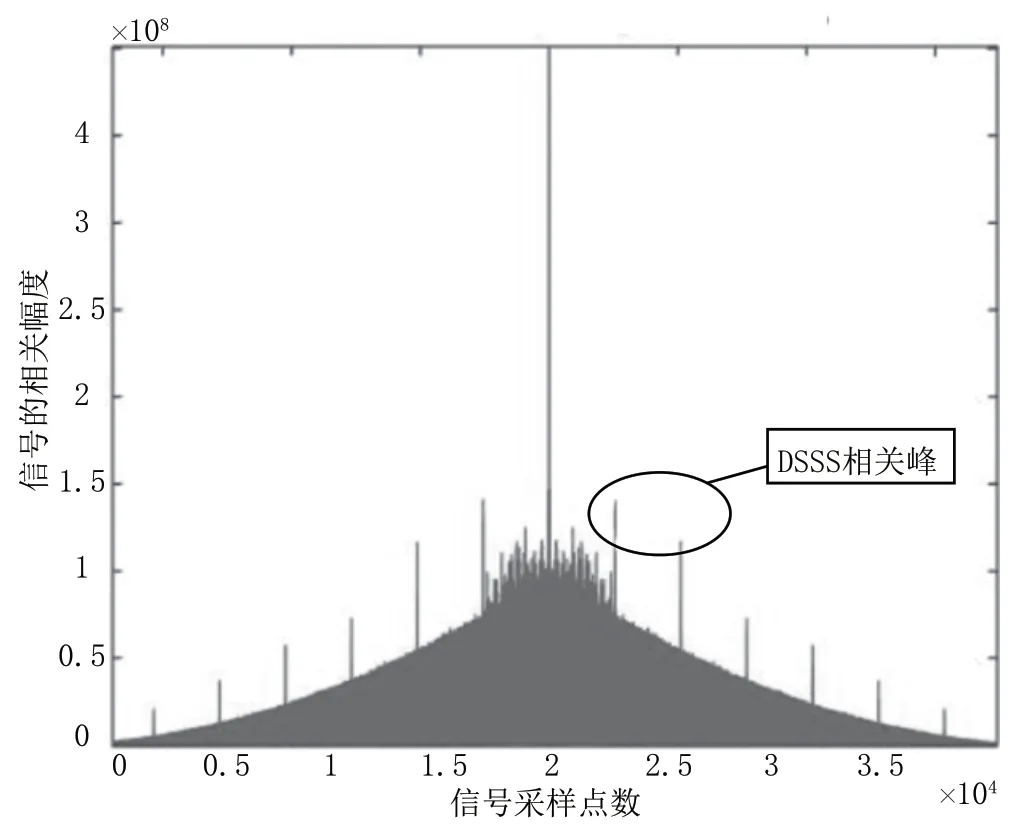
图6 多重相关峰非中心位置处
由于中心峰值的相对较大强度,为了更好地选择识别阈值,因此需要抑制τ=0 处的峰值,从而进一步提高了鲁棒性。此外,与DSSS 信号的相关峰值相比,其他类型信号的循环相关处理结果仅有一个峰值幅值较大,且最高峰值在相关平面上以τ=0为中心。
对DSSS 扩频信号和QPSK 信号、16-QAM 信号分类识别的示意图如图7 所示。QPSK 信号和16-QAM 信号都不存在多重相关谱线。
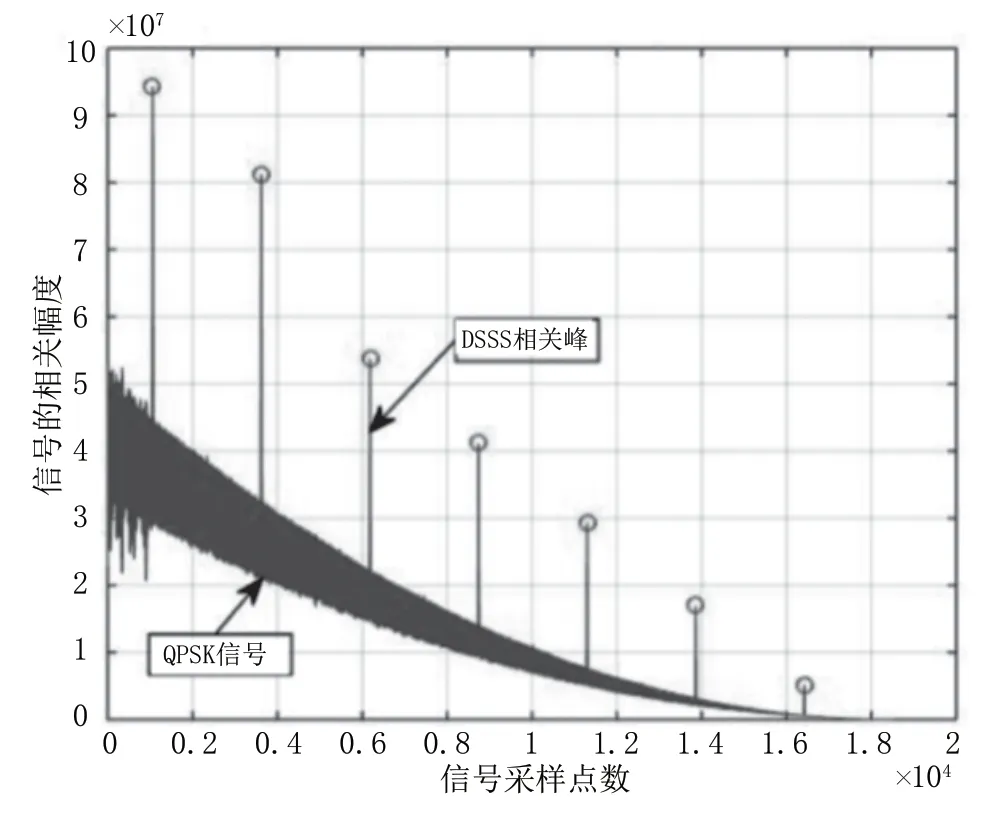
图7 DSSS 信号与QPSK 信号的识别分类
下面对无人机通信链路中扩频信号识别改进的思路步骤进行概述:
(1)对接收采样信号延迟相乘,并进行自适应滤波处理。即求取信号与其在延迟τ下的乘积得到扩频码速率,从而可在码速率位置处开展对峰值的快速搜索,并通过可调节步长的LMS 算法实现对干扰噪声的有效抑制;
(2)对步骤(1)的计算输出结果进行分段相关计算,即可先分为n段,设信号输入序列总长度为N,则,M为相关谱的窗长度,然后求取出分段相关累积的结果;
(3)根据多重相关特性实现噪声的进一步抑制,捜索求取R(τ)各分段相关的累积最大值,将大于阈值的峰值点以及延迟τ的位置进行记录,并判断τ的间隔是否相等。满足上述条件时,即可识别出DSSS 信号。
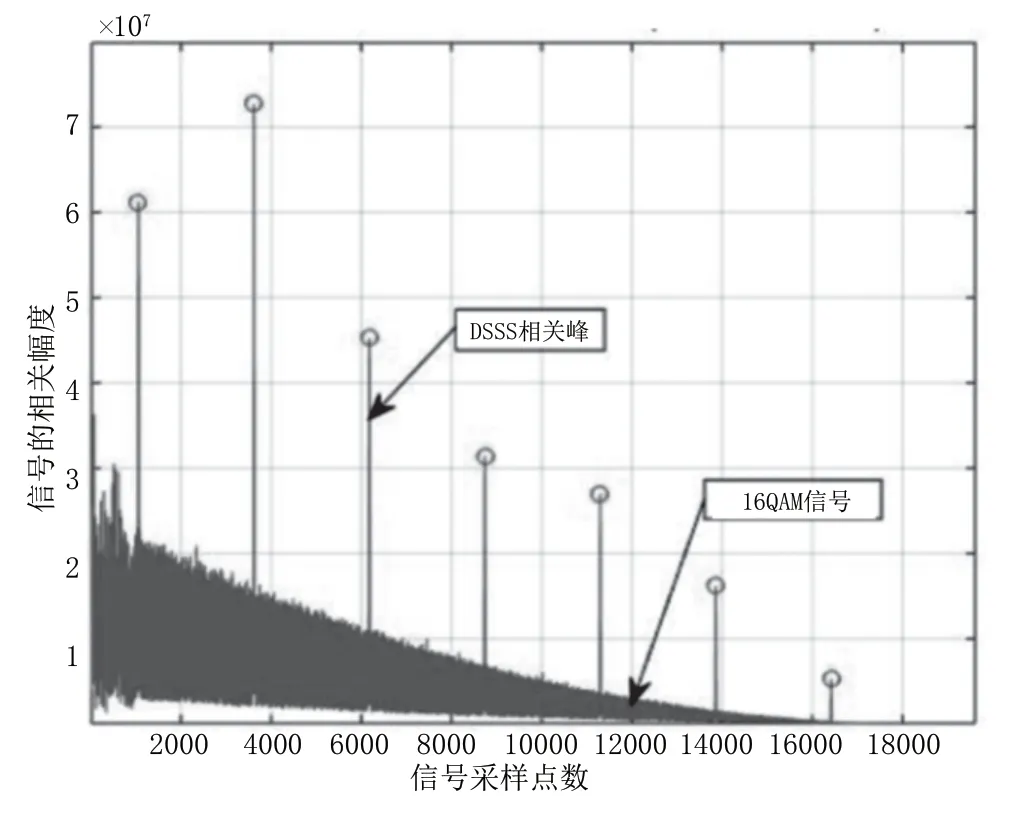
图8 DSSS 信号与16-QAM 信号的识别分类
3 仿真分析
对本文改进算法进行MATLAB 仿真试验验证。仿真参数设置为:接收的无人机扩频信号采样率为200 MHz,载频为60 MHz,扩频码速率为10 Mb/s,样本点数取为8 192,扩频码为M 码序列。Monte Carlo 仿真次数为1 000 次。选用过去的一些思路包括基于频域分析的识别方法、基于六阶矩特征的识别法和本文新改进方法进行比较,识别性能曲线如图9 所示。
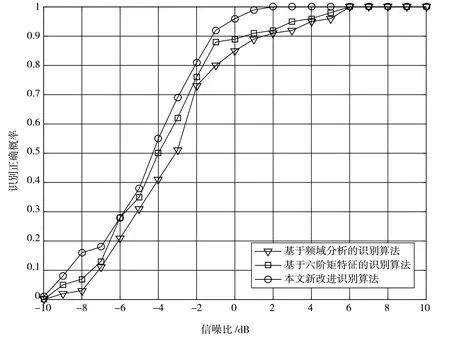
图9 本文新算法和过去算法的性能比较曲线
对图9 分析可得出,本文的新算法可实现对DSSS 信号的正确识别,且在低信噪比条件下,新方法的检测效果相对优于过去的方法,性能获得了提高。
4 结语
本文对无人机通信链路中扩频信号有效识别是信号监测研究中受到最新广泛重视的问题,在对过去的一些方法开展改进的基础上,设计拓展实现新的算法思路。该算法是一种基于可调步长自适应滤波和多重相关累积特征的识别算法。新改进思路具有良好的抗噪性,无需先验信息,收敛速度快,适用于实际应用环境中对无人机链路中DSSS 扩频信号的高效处理。此外,仿真试验验证了新方法的性能,比起过去的一些思路具有更高的识别率,鲁棒性好,且计算量相对较小,可为扩频信号分析识别提供一种更实用的手段,并对通信信号监测技术领域的研究贡献力量。

