基于直觉模糊集合的精确输入模糊输出的模糊回归模型

翟 忱, 曲智林

(东北林业大学 理学院, 黑龙江 哈尔滨 150040)

回归分析是一种用于研究因变量与自变量之间关系的方法,而模糊回归模型中涉及到的变量有模糊变量。模糊回归模型首先由Tanaka等[1]提出,并通过最小化模糊性准则,采用线性规划的方法求解模型的模糊参数。Phil[2]提出了模糊最小二乘法准则,从最小二乘法的角度研究了模糊回归模型,根据模糊数之间的各种距离测度,通过最小化预测模糊值和给定模糊数据之间的总平方误差来估计模型的参数。模糊最小二乘法因可以提供一个更精确的估计结果而被广泛应用。Hosseinzadeh等[3]基于高斯模糊数,研究了精确输入高斯模糊输出的模糊回归模型,采用非线性规划的方法求解模糊参数。Gong等[4]基于三角形模糊数,提出了模糊输入、模糊输出的模糊线性回归模型,采用模糊最小二乘法求解模糊参数,并将模型应用到员工绩效评价中。Hassanpour等[5]研究了基于梯形模糊数的模糊输入、模糊输出的模糊线性回归模型。

Atanassov[6]引入了直觉模糊集的概念。经典模糊集通过隶属度来确定模糊集合,直觉模糊集合同时考虑隶属度、非隶属度和犹豫度这3方面信息,更适用于处理一些模糊性问题,更符合实际情况。直觉模糊集合的提出拓展了模糊集理论,将模糊回归模型扩展到直觉模糊环境中也是一个重要的课题。Arefi等[7]针对对称三角直觉模糊数建立了模糊输入、模糊输出的模糊回归模型,基于直觉模糊集的加权距离,通过模糊最小二乘法求解模型的直觉模糊参数。Parvathi等[8]同样针对对称三角直觉模糊数建立了模糊输入、模糊输出的模糊回归模型,采用线性规划的方法求解模糊参数。Chen等[9]采用三角直觉模糊数,基于最小绝对偏差准则建立数学规划问题,研究了模糊输入模糊输出的模糊回归模型。在实际情况中,经常会遇到精确输入模糊输出的模糊回归问题。如,树木的生长状态的“好”与“坏”是模糊信息,而温度、降水量、太阳辐射等影响因素是精确数据。因此,研究精确输入、模糊输出的模糊回归问题是有意义的。本文将基于LR型直觉模糊数,建立精确输入模糊输出的模糊回归模型,来处理更符合实际情况的模糊性问题。

1 直觉模糊集合

定义1[6]设X是一个非空集合,将X上形如

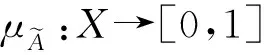
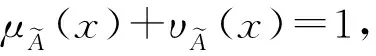
定义2[10]称

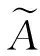
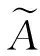
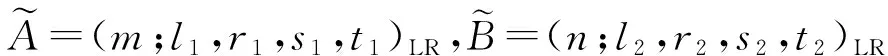
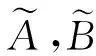
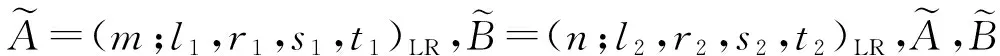
其中,

2 直觉模糊回归模型及其参数估计

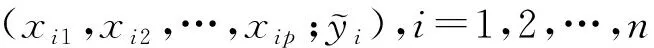
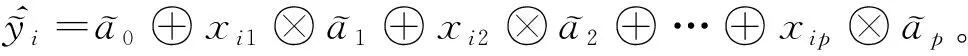
(1)

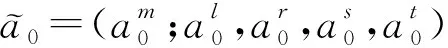
根据定义4,可得

(2)

最小。

根据定义5,可得

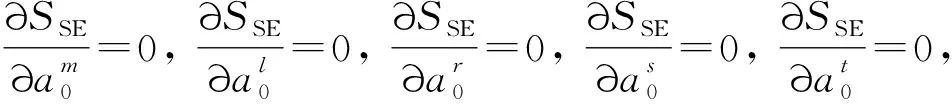
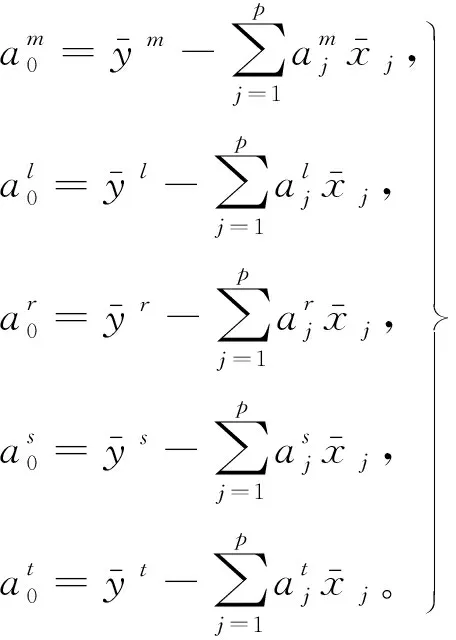
(4)

将式(4)代入式(3),可得

引入如下符号:

若XcTX是非奇异矩阵,可得

则参数估计的结果为

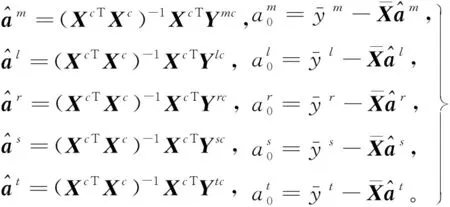
(6)

3 模糊回归模型的检验

Arefi等[7]基于直觉模糊集合之间的相似度定义了平均相似度来检验模型的拟合程度。该方法通过计算预测值与观测值之间的相似度来检验模型的拟合程度,计算过程中需要计算预测值与观测值的隶属度与非隶属度,计算过程较为复杂。本文根据定义5,定义了模型(1)的离差平方和以及回归平方和,建立了模型(1)的模糊判定系数,可通过模糊判定系数来检验模型的拟合优度。

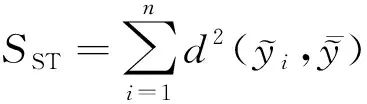
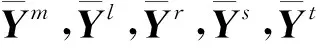
令

可得

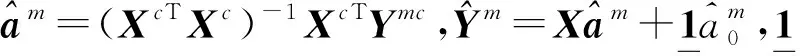
重复以上步骤,可得SST=SSE+SSR,则有如下定义

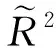
4 算 例

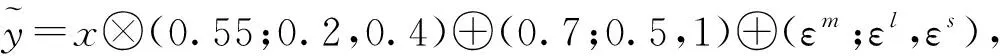
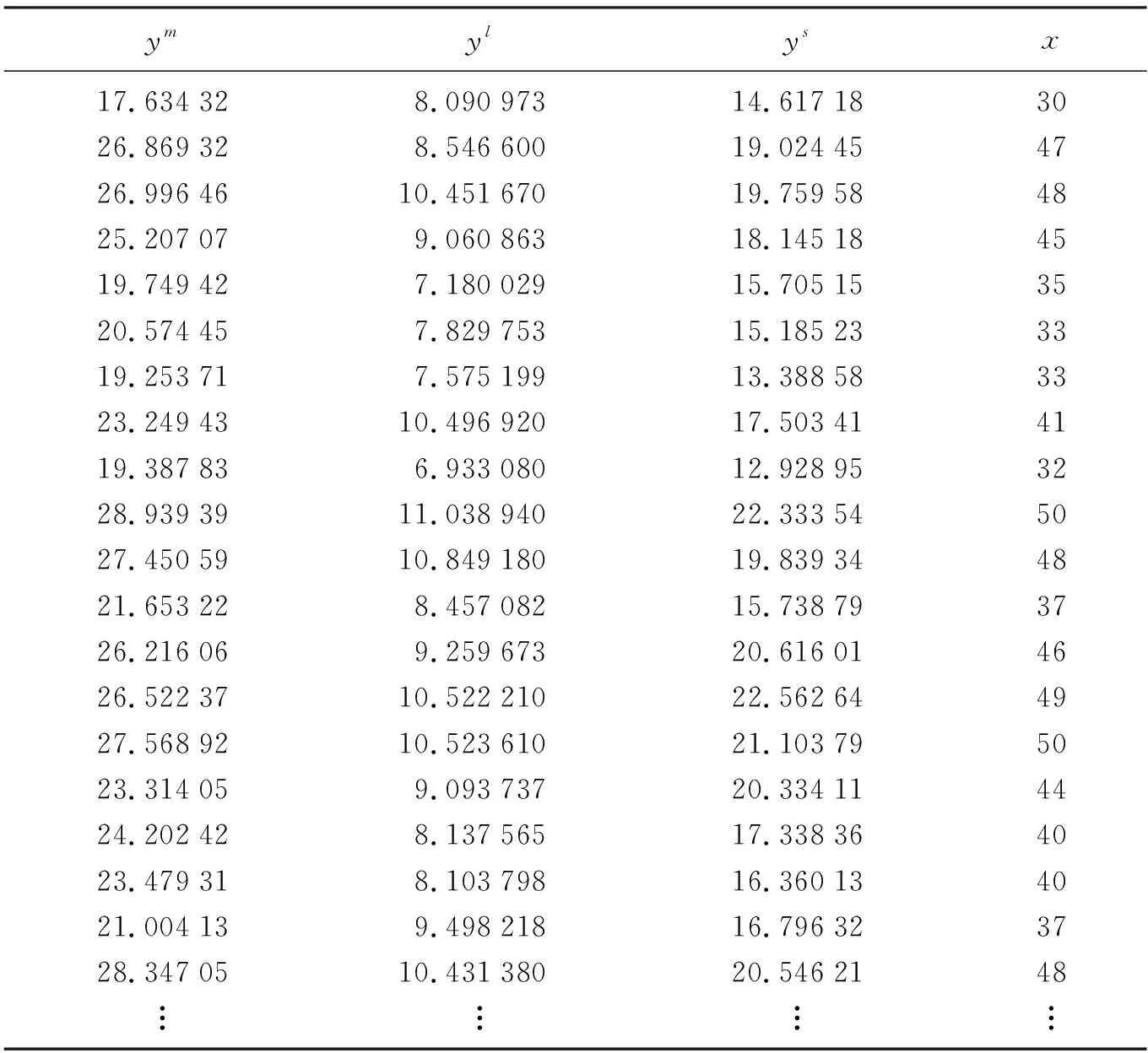
表1 随机数据Table 1 Random data

根据式(6),通过模糊最小二乘法,求出模糊回归模型为

模型拟合效果如图1所示。

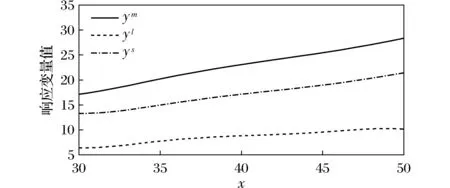
图1 拟合图像Fig.1 Fitting image

5 结 论

本文提出了基于LR型直觉模糊数的模糊线性回归模型,讨论了模糊最小二乘法在直觉模糊环境中的扩展,构建了精确输入、模糊输出的模糊回归模型。给出了模型参数的具体表达形式,且参数估计的结果不受直觉模糊样本的隶属度、非隶属度函数形状的影响,所以本文提出的模型适用于不同类型的直觉模糊样本。直觉模糊集同时考虑了隶属度和非隶属度,比经典模糊集更符合实际情况,相较于基于经典模糊集合的模糊回归模型,本文提出的模型能更好的处理现实中的模糊问题。为了检验模型拟合程度的好坏,本文定义了模糊判定系数,扩展了模型检验的方法。模糊判定系数无需考虑观测值与预测值的隶属度与非隶属度,计算方法简单易行。本文不足之处在于没有考虑直觉模糊变量分布,不能对参数进行假设检验,只能通过模糊判定系数来检验模型拟合度。参数的假设检验以及计算参数的置信区间是笔者未来的研究内容。