S -型生物化学系统的参数辨识求解方法

吴家琪, 徐恭贤

(渤海大学 数学科学学院, 辽宁 锦州 121013)

参数辨识研究是建立生物化学系统数学模型的重要组成部分,一个好的参数辨识方法可以获得较好的模型参数值。为了得到生物化学系统的最优模型参数值,国内外学者相继进行了一些参数辨识方法的研究工作[1-12]。例如,针对S -型生物化学系统的参数辨识问题,Chen等[1]提出了一种多目标进化方法;Wu等[2]应用蟑螂遗传算法对S -型生物化学系统的模型参数进行了优化辨识;Kimura等[4]采用混合差分进化方法研究了S -型生物化学系统的参数辨识;徐恭贤等[8]基于修正配置提出了一种有效的参数辨识方法,并将其应用于S -型微生物发酵模型的参数辨识中。邱添[10]利用龙格库塔法将S -型生物化学系统转化为代数方程,然后通过求解转化后的非线性优化问题得到原参数辨识问题的最优解。

本文针对S -型生物化学系统,构建了以浓度误差与浓度速率误差之和为极小化目标的参数辨识模型。结合微分方程数值解法中的基尔公式和B样条插值原理,将所构建的参数辨识模型转化为非线性规划问题。通过2个例子计算研究表明,该方法可以获得更为精确的参数辨识结果。

1 数学模型

S -型生物化学系统可以描述为

式中:Xi(i=1,2,…,n)为生物化学系统代谢物浓度;Xj(j=n+1,n+2,…,n+m)为生物化学系统酶活性;αi,βi为速率常数;gij,hij为动力阶;向量p=(αT,βT,GT,HT)T。其中α,β,G,H可分别表示为以下形式:

2 参数辨识问题

为了计算出速率常数αi,βi和动力阶gij,hij,本文建立以下参数辨识模型:

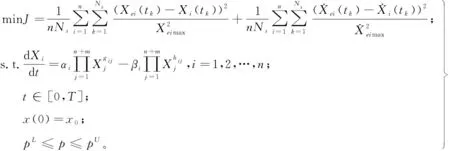
(1)

3 参数辨识问题求解方法

为了求解上述参数辨识问题,本文利用B样条插值原理和基尔公式[11]提出了一种求最优解方法,将式(1)中的微分方程组离散化为

则上述优化问题(1)可以转化为如下非线性规划问题:

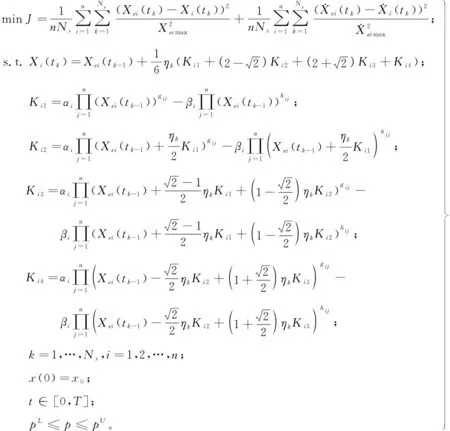
(2)

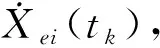
4 仿真研究

例1 考虑如下生物化学系统:

(3)

本例中初值为X(0)=(1,3)T,时间t∈[0,8],时间间隔h=0.1,参数真实值为α1=3,α2=1,β1=1,β2=1,g11=0,g12=-2,g21=0.5,g22=1,h11=0.5,h12=1,h21=0,h22=0.5。

则可得出如下参数辨识模型:

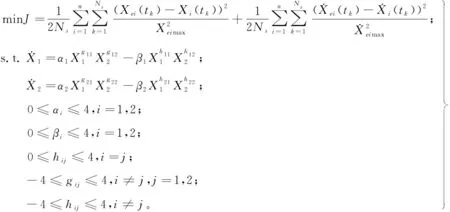
(4)

表1给出了无噪声条件下问题(4)的参数辨识值,相应的J值为4.822 902 767 244 267×10-9。由表1可以看出,本文中的方法得到的参数值与真实值比较接近。

表1 例1的辨识结果Table 1 The identification results of example 1

表2给出了结果比较,其中误差函数e为

从表2可知本文的误差e值分别比文献[8]和[10]降低了94.94%和11.58%。

表2 例1中误差e的比较Table 2 The comparison of error e in example 1

图1给出了代谢物浓度随时间变化的曲线,从图中可见,各代谢物浓度的计算值Xi(tk)与实验值Xei(tk)基本一致。

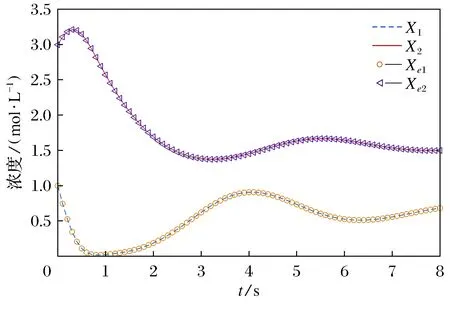
图1 例1中无噪声条件下的仿真结果Fig.1 The simulation results without noise in example 1

图2为在Xei(tk)中加入5%高斯白噪声后系统的仿真结果,从图中可见,在噪声情况下,本文方法仍能得到较好的参数辨识结果。

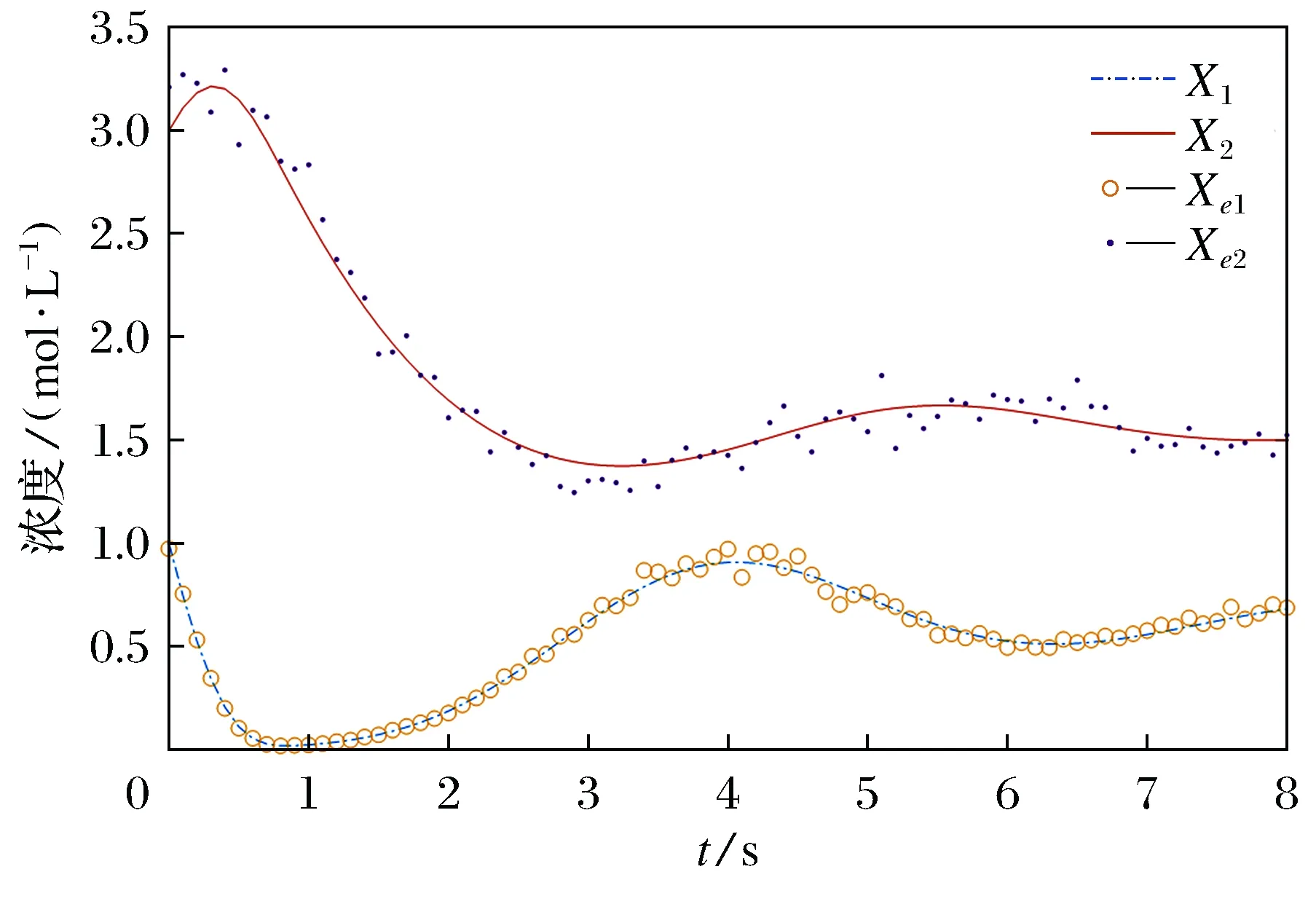
图2 例1中5%噪声条件下的仿真结果Fig.2 The simulation results under the condition of 5% noise in example 1

例2 考虑如下生物化学系统:

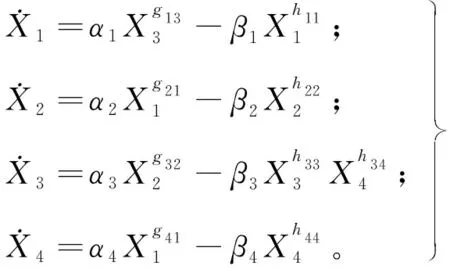
(5)

本例中初值X(0)=(1,1,2,3)T,时间t∈[0,0.5],时间间隔h=0.1,参数真实值为:α1=12,α2=8,α3=3,α4=2,β1=10,β2=3,β3=5,β4=6,g11=0,g12=0,g13=-0.8,g14=0,g21=0.5,g22=0,g23=0,g24=0,g31=0,g32=0.75,g33=0,g34=0,g41=0.5,g42=0,g43=0,g44=0,h11=0.5,h12=0,h13=0,h14=0,h21=0,h22=0.75,h23=0,h24=0,h31=0,h32=0,h33=0.5,h34=0.2,h41=0,h42=0,h43=0,h44=0.8。

则可得出如下参数辨识数学模型:

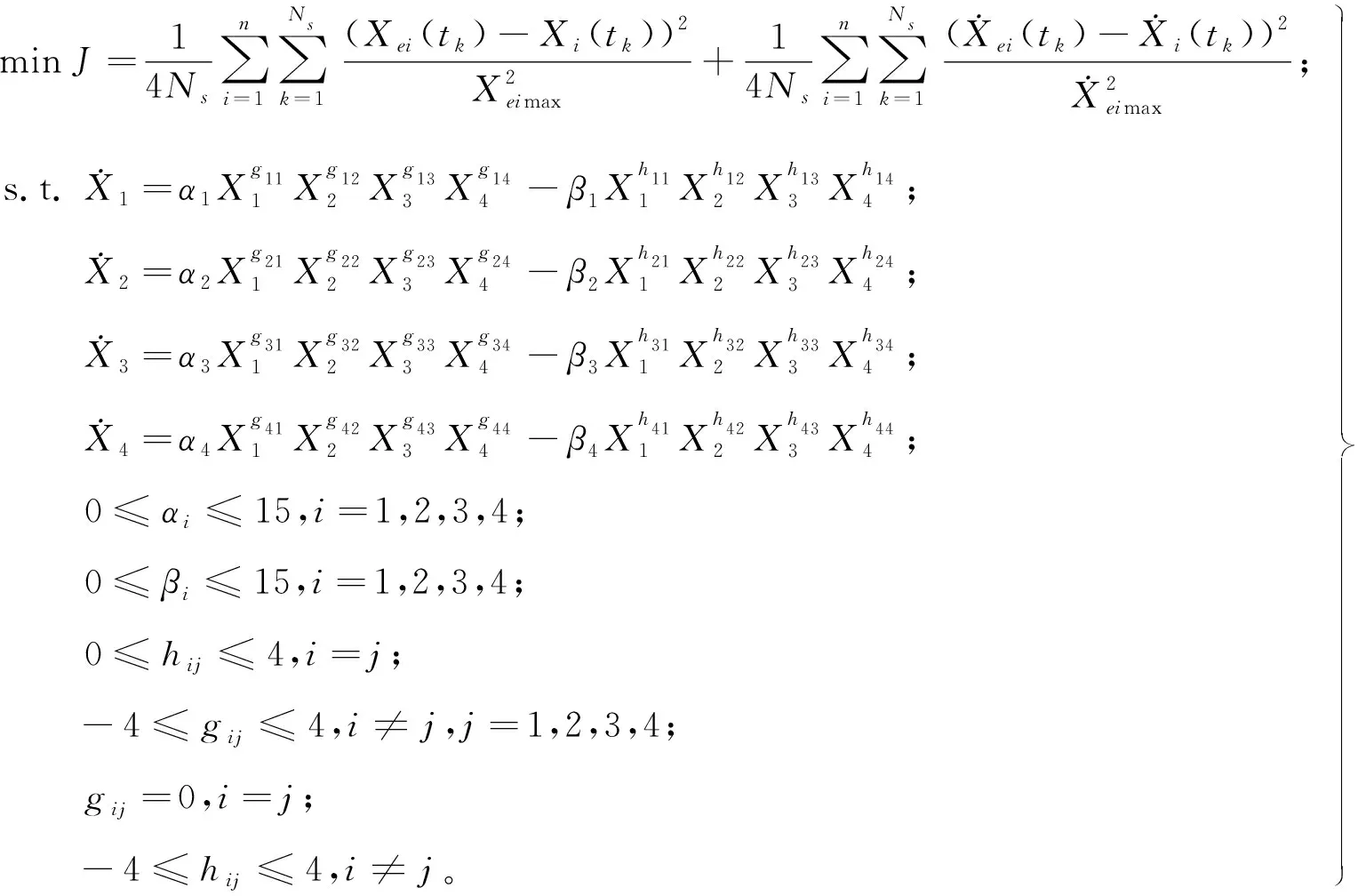
(6)

表3给出了无噪声条件下问题(6)参数辨识值,相应的J值为2.691 819 786 948 131×10-8。由表3可以看出,本文中的方法得到的参数值与真实值比较接近。

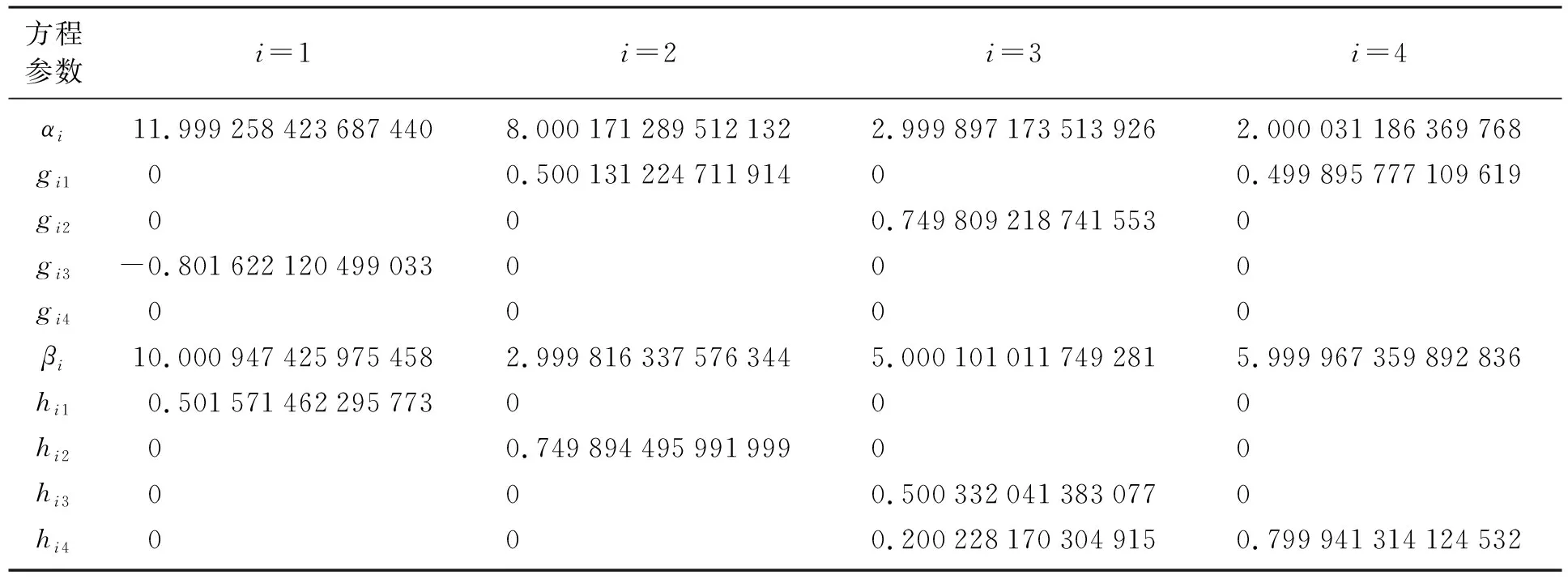
表3 例2的辨识结果Table 3 The identification results of example 2

表4给出了结果比较,从表4可知本文的误差e值分别比文献[8]和[10]降低了95.5%和12.51%。

表4 例2中误差e的比较Table 4 The comparison of error e in example 2

图3给出了代谢物浓度随时间变化的曲线,从图中可见,各代谢物浓度的计算值Xi(tk)与实验值Xei(tk)基本一致。

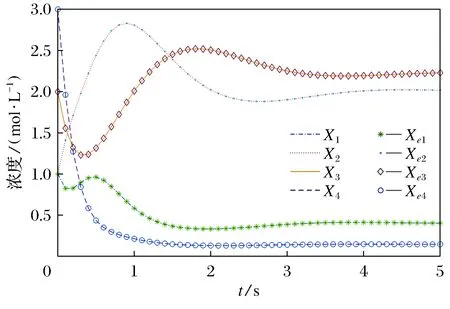
图3 例2中无噪声条件下的仿真结果Fig.3 The simulation results without noise in example 2

图4为在Xei(tk)中加入5%高斯白噪声后系统的仿真结果,从图中可见,在噪声情况下,本文方法仍能得到较好的参数辨识结果。

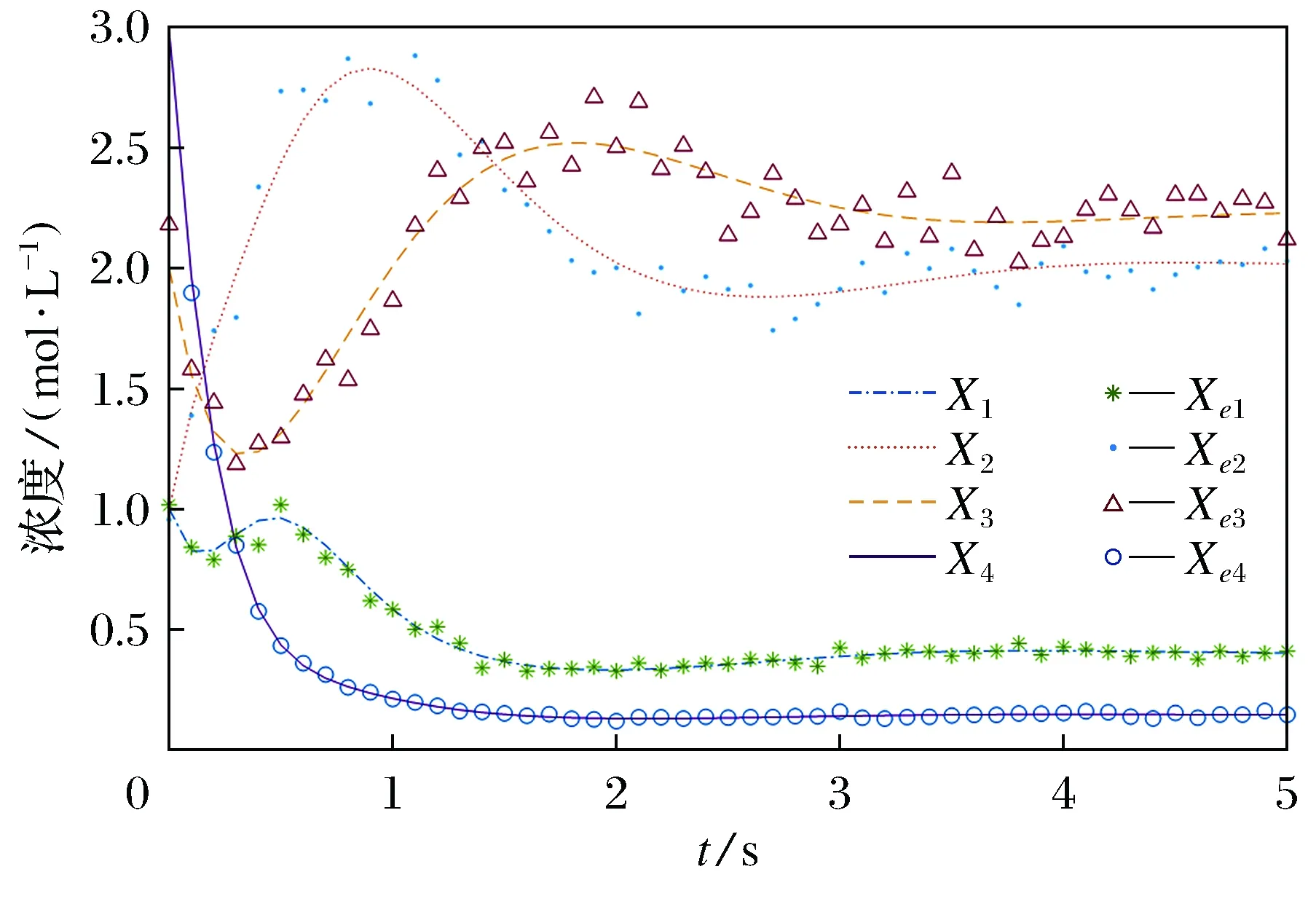
图4 例2中添加5%噪声条件下的仿真结果Fig.4 The simulation results under the condition of 5% noise in example 2

5 结 语

针对S -型生物化学系统的参数辨识问题,本文给出了参数辨识优化模型。结合微分方程数值解法中的基尔公式和B样条插值原理提出了一种求解方法。2个例子的计算结果表明,本文方法可以得到比已有文献更准确的参数值。