基于全局和局部信息融合的SVM多模态过程故障检测

郭金玉, 李 涛, 李 元

(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)

大数据时代,工业自动化技术正在快速的发展,工业系统的规模和控制系统的复杂程度都在不断提高,越来越体现其非高斯、多工况的特点,同时也会造成故障发生概率不断增大,因此对控制系统精度和安全可靠性也提出了更高的要求。

主元分析(principal component analysis, PCA)作为工业过程中对故障进行诊断和检测的最基础手段,一直发挥着重要的作用,被广泛应用在多种场景,同时也衍生出多种新的故障检测方法[1-3]。PCA在实现降维的同时,能够保留数据的全局信息,很好地反映数据变化。由于PCA处理的数据需要满足高斯分布和线性分布的前提假设,并且在降维的同时会导致局部信息丢失,因此具有一定的局限性。为了提高PCA在多模态过程中的故障检测性能,郭金玉等[4]提出改进局部熵主元分析的故障检测方法,通过构造改进局部熵数据剔除多模态特性,并建立主元分析故障检测模型,实现对故障数据的有效检测。此外,为了改善全局算法在故障检测中的不足,Hu等[5]将局部保持投影算法(locality preserving projections, LPP)应用于工业过程故障监测。LPP算法[6-7]是一种用于提取数据特征的降维方法,它能够很好地保留数据的局部信息,主要考虑的是保持数据中近邻点之间的结构,其本质是对拉普拉斯特征映射的线性逼近。为了提高LPP算法的故障检测性能,Guo等[8]提出差分局部保持投影(difference locality preserving projections, DIF-LPP)算法,利用差分方法剔除数据非线性和多模态结构,然后运用LPP进行故障检测。为了进一步推广LPP在非线性生产过程中的应用,Luo等[9]提出核全局-局部保持投影算法(kernel global-local preserving projections, KGLPP)。

Vapnik[10]于1995年提出支持向量机(support vector machine, SVM),由于其强大的泛化能力和在解决各种分类问题方面的诸多优势,被国内外学者广泛研究学习[11],成为机器学习中的经典算法。SVM算法对数据进行故障检测时,需要运用正常和故障数据对SVM模型进行训练,该训练过程使得SVM能够学习到正常和故障数据的特征变化,更好地进行故障检测。面对高维数据,Guyon等[12]提出线性支持向量机递归特征消除(support vector machine recursive feature elimination, SVM-RFE)算法,即线性SVM-RFE。Shieh等[13]通过使用总体排序或特定类型的排序来选择关键特征,提高线性SVM-RFE对样本特征的提取,改善SVM的性能。由于故障检测与诊断并不只是线性问题,Xue等[14]引入高斯核SVM-RFE提取非线性特征进行故障检测与诊断,该方法关键在于核参数的选择,通过对比选择出最优参数,建立一种先进的故障检测与诊断框架。

对高维数据,SVM的运行时间较长。为了降低SVM的运行时间,需要对数据进行特征提取和降维,而SVM算法性能的高低依赖于数据特征提取的好坏。在处理多模态过程时,数据会出现非高斯性等问题,这也会影响SVM算法的故障检测性能。因此,为了有效地提高SVM对多模态过程的故障检测性能,提出一种基于全局和局部信息融合的SVM多模态过程故障检测方法。结合局部概率密度方法,本文将多模态问题转化为单模态问题,然后运用PCA算法和LPP算法分别提取数据的全局信息和局部信息,并融合全局和局部信息用于建立SVM故障检测模型,实现对多模态过程的故障检测与监视。

1 基于全局和局部信息融合的SVM多模态过程故障检测

1.1 基于局部概率密度的多模态过程预处理算法

在现代工业生产过程中,过程数据往往存在严重的非线性、多模态特性,传统的故障检测算法直接应用于多个模态会影响故障检测的结果。因此,本文运用局部概率密度算法对原始数据进行预处理,剔除数据的多模态结构。通过一个人工合成的多模态数值例子来验证局部概率密度算法剔除数据多模态结构的有效性。在此数据中每个样本有2个变量,并且线性相关。变量x1服从[0,1]均匀分布;变量x2服从[1,2]均匀分布;e为服从均值为0、标准差为0.1的正态分布的噪声。具体数据来源于

x2=x1+e。

(1)

通过对模型(1)进行适当的位置转换,可以获得2个模态的数值例子,在每个模态下分别生成400个样本。图1是2个模态的数据分布散点,图2是运用局部概率密度算法对原始数据进行预处理后的数据散点。通过图1和图2的比较,可以直观地看出局部概率密度算法能够有效地将多模态结构转化成单模态结构,进而验证了该算法的有效性。

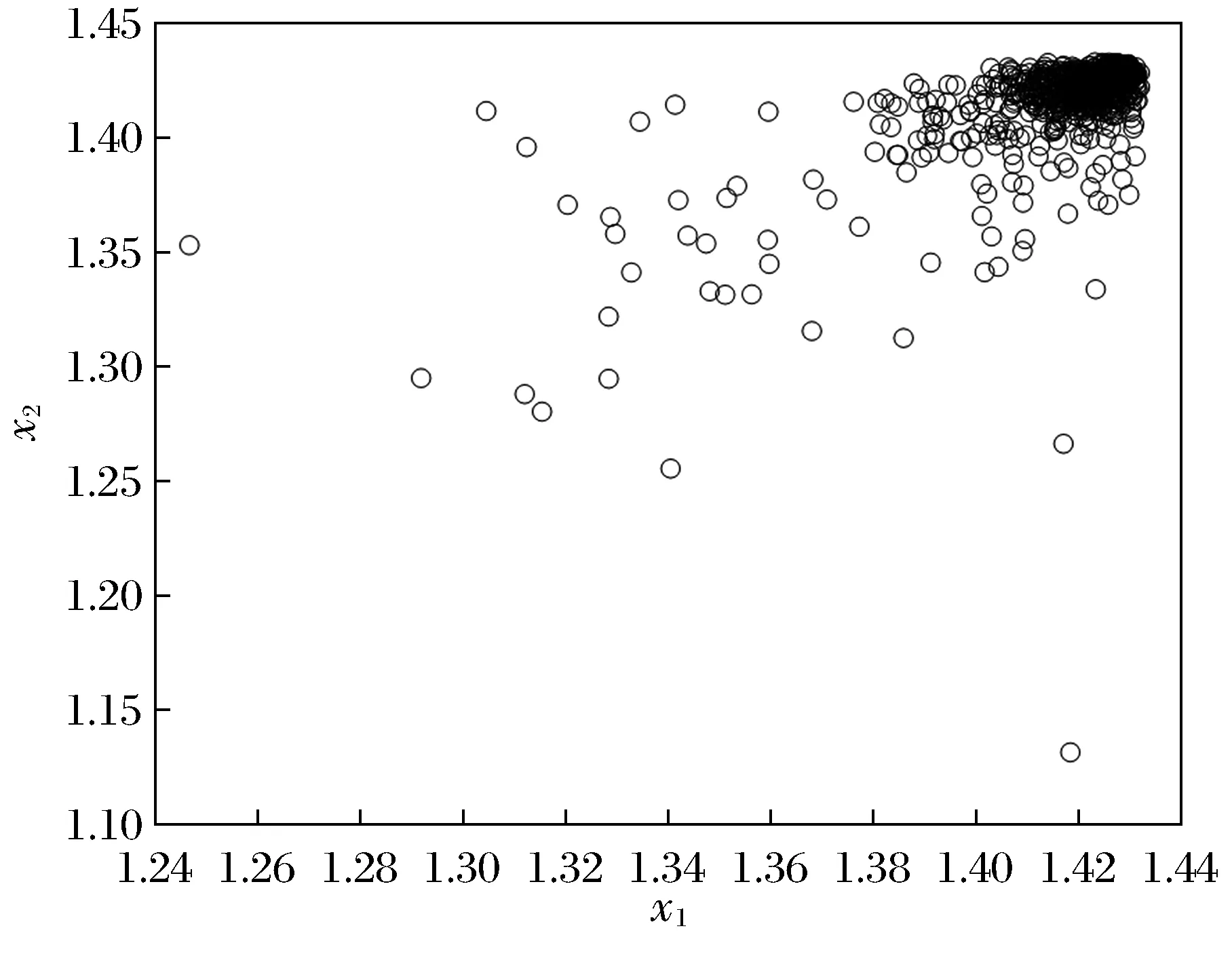
图2 局部概率密度数据散点Fig.2 Scatter plot of local probability density data

1.2 主元分析算法

在多元统计分析中,主元分析能够达到降维的目的,提取原始数据的主要特征。假设数据集为Xm×n,其中m是样本数,n是变量数。定义标准化后样本集X的协方差矩阵为

(2)

对协方差矩阵S进行特征值分解,计算出特征值和特征向量,并按照特征值大小降序排列。接下来求取主元个数z,现有的选择主元个数的方法包括累计方差贡献率(cumulative percent variance,CPV)、碎石检验、平行分析和重建误差准则等方法,但对于哪种方法更好,目前尚未达成共识。因此,本文根据累计方差贡献率求取主元个数z。当CPV≥85%时,所获得的主元能够代表样本的主要特征[15],计算方式如下:

(3)

式中,λi为协方差矩阵的特征根,其中由前z个特征向量构成的矩阵就是负载矩阵P。根据式(4)计算主元矩阵T1,提取数据的全局特征信息。

T1=XP。

(4)

用PCA算法对上述多模态数值例子进行处理,得到如图3所示的主元图。从图中可以看出,经过PCA处理的数据仍然是2个模态,说明PCA算法无法剔除数据的多模态结构,这会影响PCA算法的故障检测性能。

图3 PCA算法处理后的数值例子主元Fig.3 Principal component plot of numerical example preprocessed by PCA algorithm

1.3 局部保持投影算法

PCA能够将高维数据投影到包含原始数据方差最大的低维空间上,并且能够剔除变量之间的相关性。由于PCA是一种二阶算法,这意味着它考虑的仅是给定数据的均值和方差-协方差,因此在实际工业过程中缺乏对具有复杂分布的数据提供局部信息表示的能力。由于流形学习算法具有保持局部结构信息的能力,LPP算法能够使投影数据与原始数据的近邻结构得到保持,可以很好地保留数据的局部特征信息。算法的核心是寻找投影矩阵A,将m个高维样本点映射到低维特征空间中,即Y=XA,使Y尽可能地代表X。

首先构造目标函数,使局部近邻结构在投影前后相似,如式(5):

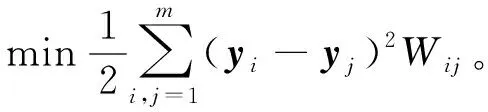
(5)

式中:yi是xi在低维空间中对应的样本点,即yi=xia,其中a为投影矩阵A的列向量;W为权值矩阵,Wij表示顶点xi和xj路径的权重,计算方法为Wij=exp-(‖xi-xj‖2)/t,故式(5)可表示为

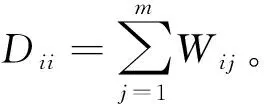
XTLXa=λXTDXa。

(7)

式(7)的p个最小特征值对应的特征向量即为投影矩阵A。同样地,LPP采用主元矩阵刻画数据的局部特征信息,

T2=XA。

(8)

用LPP算法对上述多模态数值例子进行处理,得到如图4所示的主元图。从图中可以看出,经过LPP处理的数据仍然是2个模态,说明LPP算法也无法剔除数据的多模态结构,这会影响LPP算法的故障检测性能。

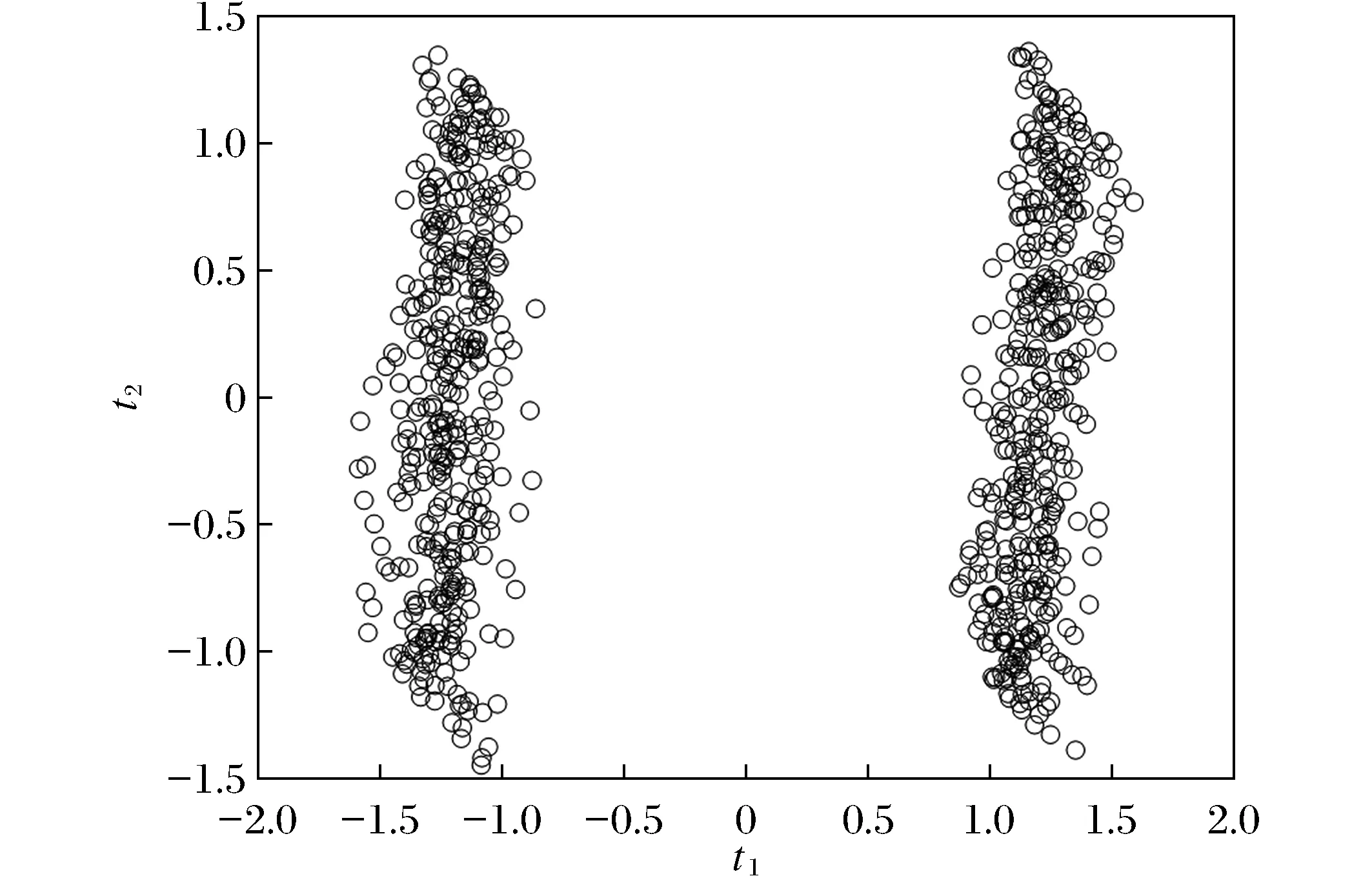
图4 LPP算法处理后的数值例子主元Fig.4 Principal component plot of numerical example preprocessed by LPP algorithm

本文首先运用局部概率密度算法剔除多模态结构,然后运用PCA和LPP分别提取数据的全局特征和局部流形特征。

1.4 全局和局部信息融合的SVM算法

将包含全局和局部特征信息的主元矩阵进行融合,即T=[T1,T2],2者融合后在低维空间能最优地保留数据的局部和全局信息。运用正常和故障数据的主元矩阵T作为SVM模型的输入,对SVM进行训练,获得判别分类函数。建立模型之后,SVM能够学习到正常和故障数据的特性,从而将数据正确分类。

SVM算法在解决数据集规模相对较小、样本呈现非线性和局部极小值等问题方面具有许多优点。在样本训练集空间T中找到一个最大分离超平面,才能把不同类别的样本有效地分类。假设样本训练数据集为T={(t1,y1),(t2,y2),…,(tm,ym)},yi∈{-1,+1},ti∈z+p在该样本训练集空间中找到一个最大分离超平面,把不同类别的样本有效分类,这是分类学习最基本的思想。SVM对指定数据分类的超平面如下:

wTt+b=0。

(9)

式中:w=(w1,w2,…,wz+p)T是权重向量;b是位移项;t为样本空间中任意点。为了找到最大间隔的超平面,实现最大程度分类,需要找到合适的参数w和b,使得间隔最大,达到最好的分类效果。

考虑到一些无法分类的样本以及支持向量机在一些样本上分类出错的情况,为了提高支持向量机的容错率,引入惩罚因子C和松弛因子ξ。松弛因子的引入使SVM分类具有一定的容错性,能够忽略落在隔离带中的样本点对超平面划分的影响,使超平面不用朝这些样本点方向移动。惩罚因子通常设置为一个常数,惩罚因子越大,要求松弛因子的值尽量小,即对噪声的容忍度越小,其主要起到权衡的作用。那么SVM的基本型可表示为

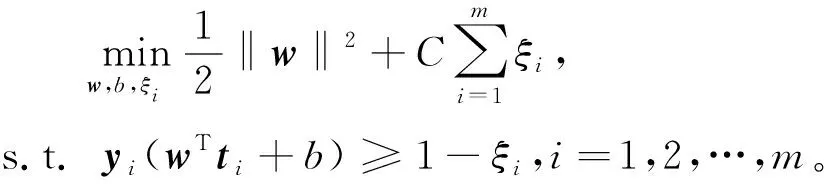
(10)

其中ξi≥0,C>0是一个常数。

为了求解式(10),需要将其转化为“对偶问题”,运用拉格朗日乘法求解,则该问题的拉格朗日函数可写为

(11)

其中αi≥0,μi≥0是拉格朗日乘子。通过对上式求解,可以得到该模型为

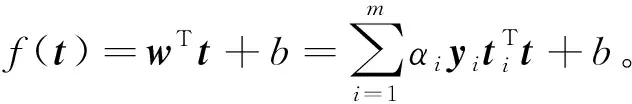
(12)

在实际工业过程中,数据并不只是服从线性分布,更多情况是非线性数据,为了对数据更好地分类,需要通过非线性映射φ(t)将其投影到高维特征空间。为了避免高维运算,引入核函数,通过核函数计算后该模型为

(13)

式中K(·)是核函数。因此,SVM在对数据进行分类时,若数据呈现线性分布,SVM对其进行线性分类,若数据呈现非线性分布,SVM可以将映射到高维空间,并引入核函数解决高维计算问题,进而高效准确地对数据实现分类。

1.5 基于全局和局部信息融合的SVM多模态过程故障检测

PCA、LPP和SVM方法适用于单模态过程的故障检测,然而工业过程通常包含多个模态,如果这些算法直接应用于多模态过程,其监视和检测性能就会下降。为了改进多模态过程的故障检测性能,本文首先利用局部概率密度方法[16]将多模态数据处理成单模态数据,然后应用本文方法进行过程监视与检测。基于全局和局部信息融合的SVM多模态过程故障检测具体步骤如下:

1) 在正常操作条件下收集历史数据集X1=[x1,x2,…,xm]T∈m×n;

2) 对历史数据集进行标准化处理,得到矩阵X2;

3) 运用式(14)计算X2的局部概率密度矩阵

(14)

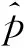
4) 运用PCA和LPP算法分别提取数据的全局和局部特征信息,并将两者融合,作为SVM的输入,运用正常和故障数据的全局和局部融合的信息训练SVM模型获得判别分类函数;

5) 对测试数据进行预处理,对局部概率密度矩阵提取全局和局部特征信息,将两者融合后运用SVM模型进行分类,得到最终分类结果。通过该步骤分类后,正常数据划分成一类,定义为标签0,故障数据划分成另一类,定义为标签1。

2 仿真结果与分析

Tennessee-Esatman(田纳西-伊斯曼)过程已成为国际上通用的工业过程模型仿真平台[17],在故障检测和诊断领域,被国内外学者广泛使用。TE过程变量众多,其中2个气液放热反应会产生2种主产品,此外,还和5个主要操作单元等共同组成TE过程。TE过程模拟21种预编程故障,丰富多样的故障类型能够真实反映实际工业过程中的众多问题。改变该过程中产物G和H的比例,可以对其进行各种操作模式。由于多模态过程具有不稳定性, 受各种变量影响较大,所以采用多种控制策略来解决该问题。本文采用的是分散控制,由Ricker提出, 可从文献[18]提供的网站上下载其仿真代码。本文对该过程中的模态1和模态3两个模态进行研究。

从模态1和模态3中分别选取600个正常样本组成多模态训练数据集。此外,从两个模态中分别选取400个故障样本组成多模态测试数据集。需要注意的是,SVM和本文方法在训练模型时需要加入故障数据,因此,还需要从2个模态中分别选取400个故障样本用于SVM和本文方法的训练。

在TE多模态过程仿真中,以故障类型1、2、3、4、5、7、8和10为例,对本文方法进行分析。其中PCA和LPP的主元个数通过85%累计方差贡献率确定,T2和SPE统计量的99%控制限通过核密度估计方法计算。通过寻优测试将SVM和本文方法中的惩罚因子设置为0.8,窗宽g设置为0.45。图5是正常训练数据中变量3和变量5的序列图,可以看出数据呈现2个模态。通过局部概率密度方法对多模态处理后,样本由多模态变成单模态,如图6所示。

(a) x3(b) x5

(a) x3(b) x5

利用PCA、LPP、SVM和本文方法分别对预处理后的单模态数据进行故障检测,故障5的检测结果对比如图7所示。从图中可知,传统PCA和LPP算法的检测效果并不理想。由于PCA是线性算法,样本的非线性分布会导致算法的检测性能下降,因此检测效果不理想。LPP算法的统计指标需要服从高斯分布的前提假设,当这种假设不满足时,会降低其检测性能。与PCA算法相比,LPP算法的故障检测性能更优。这是因为PCA算法提取数据的全局特征,而LPP算法提取数据的局部特征,提高了故障检测性能。SVM算法对故障样本的分类准确性高于PCA和LPP,这得益于SVM算法在训练数据时能够学习到2类样本的特征变化, 因此在模型测试时能够有效地识别故障样本。本文方法通过融合PCA提取的全局特征信息和LPP提取的局部特征信息,增强了对样本特征信息的提取能力,使得SVM能够更好地学习到2类样本的特征变化情况,提高了故障检测性能。与传统PCA、LPP和SVM算法对比,本文方法的故障检测效果最佳,验证了本文方法在多模态过程故障检测中的有效性。

(a) T2-PCA(b) SPE-PCA(c) T2-LPP(d) SPE-LPP(e) SVM(f) 本文方法

表1是4种算法对8种不同类型故障的检测率对比。从表中可知,对8种不同类型的故障,本文方法的故障检测率相较于其他算法都有不同程度的提高,验证了该算法的有效性。

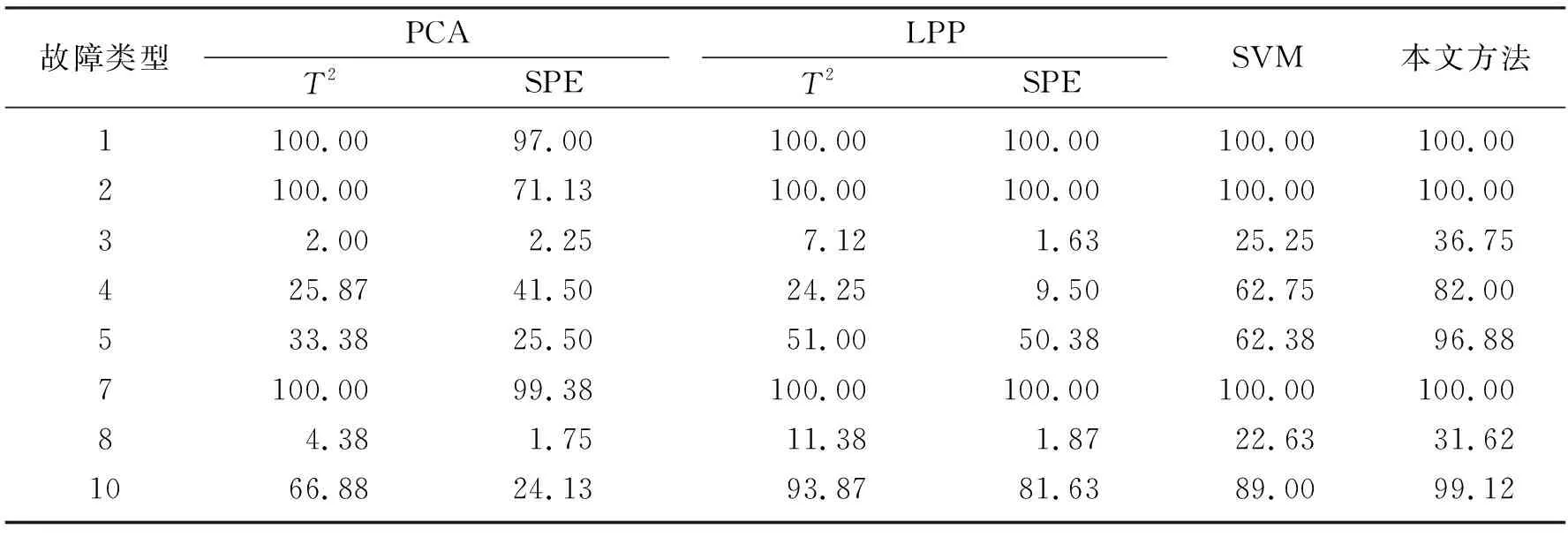
表1 4种算法的故障检测率对比Table1 Comparisons of fault detection rates of 4 algorithms %

3 结 论

提出一种基于全局和局部信息融合的SVM多模态过程故障检测方法。引入局部概率密度函数将多模态数据转化为单模态数据,消除多模态和非高斯特性。在此基础上,将PCA和LPP算法提取的全局特征信息和局部特征信息融合,增强对样本特征信息的提取能力,提高SVM算法的故障检测性能。将本文方法应用于TE多模态过程中,仿真结果表明,与传统PCA、LPP和SVM方法比较,本文方法能够提高故障检测率,验证了该方法的有效性。