基于马氏距离kNN的多模态过程故障检测

王晓云, 王东琴, 郭金玉

(1. 沈阳理工大学 机械工程学院, 辽宁 沈阳 110159;2. 沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)

随着自动化和智能化技术在工业生产中的广泛应用,生产过程中的监控环节越来越重要,为适应多模态的生产过程,基于多模态间歇过程的故障诊断就显得尤为重要。许多学者对基于数据驱动的故障检测技术进行了研究,主元分析(principal component analysis, PCA)[1]是一种对数据进行化简的传统多元统计过程监控方法(multivariate statistical process monitoring,MSPM)方法,也是较为成熟的算法,但是它提取的是线性特征,无法有效地检测非线性和多模态过程,而实际工业生产过程中更多的是非线性和多模态过程,所以它在纷繁复杂的多模态间歇过程当中,难以得到广泛应用。

很多研究人员对多模态工业过程故障检测进行了多角度、深层次的研究,并提出了一些新的故障诊断手段。文献[2]利用k近邻(k-nearest neighbor,kNN)的方式进行故障检测,并在半导体蚀刻工艺过程中得到成功应用。该方法能够对非高斯、非线性的多模态间歇过程进行故障检测,缺陷在于该算法在处理样本容量大的数据集时,使系统的计算负载和存储负担过大,每次分类都会进行重新计算导致计算量增加。除此之外,当多模态样本方差较大时,该算法也无法得到理想的处理结果。文献[3]提出的局部离群因子算法,能够利用单个模型对多模态过程进行有效监控,但该方法缺陷在于检测效果容易受参数影响,稳定性差,而且计算量也较大。文献[4]运用局部密度估计方法对多模态过程进行监控,能够迅速检测出多工况过程的故障。文献[5] 研究了一种基于时空近邻标准化和局部离群因子的复杂过程故障检测算法,能够实现具有动态性、多模态特性或两者兼具的过程的故障检测。当前,就多工况生产而言,数据维数不断上升,存在方差差异明显和中心漂移等特点,文献[6]利用加权k近邻方法进行故障检测。由于在kNN方法中,对于多模态过程,数据与其邻域之间的距离计算从不考虑每一个单模态的尺度信息,Song等[7]提出一种基于标准化kNN(standardizedknearest neighbor,SkNN)的故障检测方法,该方法考虑了模态式内和模态式间的尺度信息,通过标准化距离来表征数据与其邻域之间的距离。此外,与基于kNN的故障诊断方法相比,基于SkNN的故障诊断方法通过构造权重来考虑不同邻域的重要性。

本文研究了一种新的基于马氏距离kNN(MD-kNN)的故障检测方法,通过分析故障数据与正常数据在空间距离关系上的差异,有效消除了模态间的方差差异,进而达到检测故障的目的。

1 基于马氏距离kNN的多模态过程故障检测

1.1 kNN方法

kNN分类算法表示任意样本均选择与它距离最近的k个邻居来代表。根据训练样本和近邻样本之间的距离分布,从而确定具有一定置信水平的阈值。kNN的故障诊断过程包括建模过程和故障检测过程,具体步骤参见文献[8]。下面具体分析本文提出的马氏距离的kNN算法。

1.2 MD-kNN算法

kNN适合用于多模态故障检测。但当同一变量在不同模态下的方差有显著差异时,kNN规则在检测多模态过程中的微弱故障时就失去其优良性能,下面通过数值例子加以说明。

图1为全部训练样本和故障样本的散点分布情况。其中,圆圈、星号以及方块分别表示第1、2模态训练样本以及第1模态的故障样本。模态1的2个变量x1、x2都呈现[0,1]的正态分布;模态2的2个变量x1、x2都呈现[15,6]的正态分布。

图1 数值例子散点分布Fig.1 Scatter plot of numerical example

将kNN方法中k的近邻数设为1,控制限可通过训练数据确定。图2为利用kNN方法对该数值例子的检测结果,圆圈、星号以及方块分别表示模态1、2训练样本以及第1模态的微弱故障样本。图2中有4个星号没有显示, 因为它们的值明显高于其他值。

从图2中可以看出故障样本的距离要大于模态1中训练样本的距离,小于模态2中训练样本的距离。传统kNN算法采用欧式距离来计算样本间的距离,其控制限是根据总体样本的检测指标值确定的,即控制限是由较大方差的模态中的样本决定的,而本例中的故障属于小方差模态的微弱故障,因此无法检测到。

图2 kNN对训练样本和一个微弱故障的检测结果Fig.2 Detection result of kNN for training samples and a weak fault

在上述分析的基础上,设计出一种新型算法,命名为马氏距离kNN(MD -kNN),马氏距离可以清晰地检测出观察样本与已知样本两者之间的距离,在识别故障和状态分类过程中非常适用[9]。马氏距离表示数据的协方差距离,与欧氏距离不同的是它考虑到各种特性之间的联系,可以衡量样本间相似度的距离,因而可以检测在不同模态下同一变量方差显著不同时的微弱故障。通过考虑数据之间的相互关系来计算样本之间的距离,样本xi与xj的马氏距离为

(1)

由式(1)可知,为确保协方差矩阵可逆,样本数量应满足i>j。故马氏距离能有效衡量数据变量之间的相互联系,欧氏距离意味着全部类别等概率呈现出来,欧式距离属于马氏距离中的一种特殊类型。目前,决策的中心位置是2种距离中心连线后的中点,详情见图3,如果两距离产生的先验概率不一致,此时采取中垂线进行决策判断将会导致结果出现误判,应该向右调整决策线,通过马氏距离获取向右移动位置的大小。

图3 类别表征Fig.3 Category representation

传统的kNN算法在计算样本间的欧式距离时不考虑模态间局部差异的情况,对检测指标进行计算,当不同模态的方差差异较大时,对微弱故障的检测性能较差。基于MD -kNN的故障检测,利用马氏距离计算各样本间的距离,不用考虑模态间不同的稀疏程度。图4为MD -kNN方法对数值例子的检测结果,MD -kNN有效地检测出了模态1的微弱故障,说明了该算法的有效性。

图4 MD -kNN对训练样本和一个弱故障的检测结果Fig.4 Detection result of MD -kNN for training samples and a weak fault

1.3 建模过程与在线检测

2 仿真结果与分析

2.1 多模态数值例子

以人工合成的多模态数值为例,应用本文提出的方法对方差差异较大的多模态过程故障检测进行验证。具体如下:

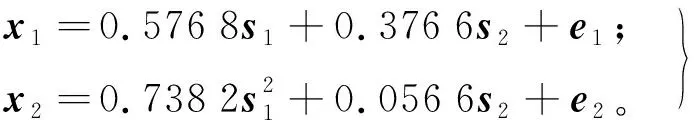
(2)

式中,模态1:s1～Uniform(-10,-7),s2～N(10,0.01);模态2:s1～Uniform(2,5),s2～N(-10,1)。其中e1,e2是服从[0,0.01]的正态分布的噪声。根据以上模型形成2种模态的数据,分别从中挑选200个正常数值作为训练样本和校验样本,再挑选6个非正常数值作为故障样本。图5为训练样本、校验样本以及故障样本的散点分布,通过图5的散点分布可知,本文研究的数值例子稀疏程度不一致的多模态模拟案例。

图5 多模态数据散点分布Fig.5 Scatter plot of multimodal data

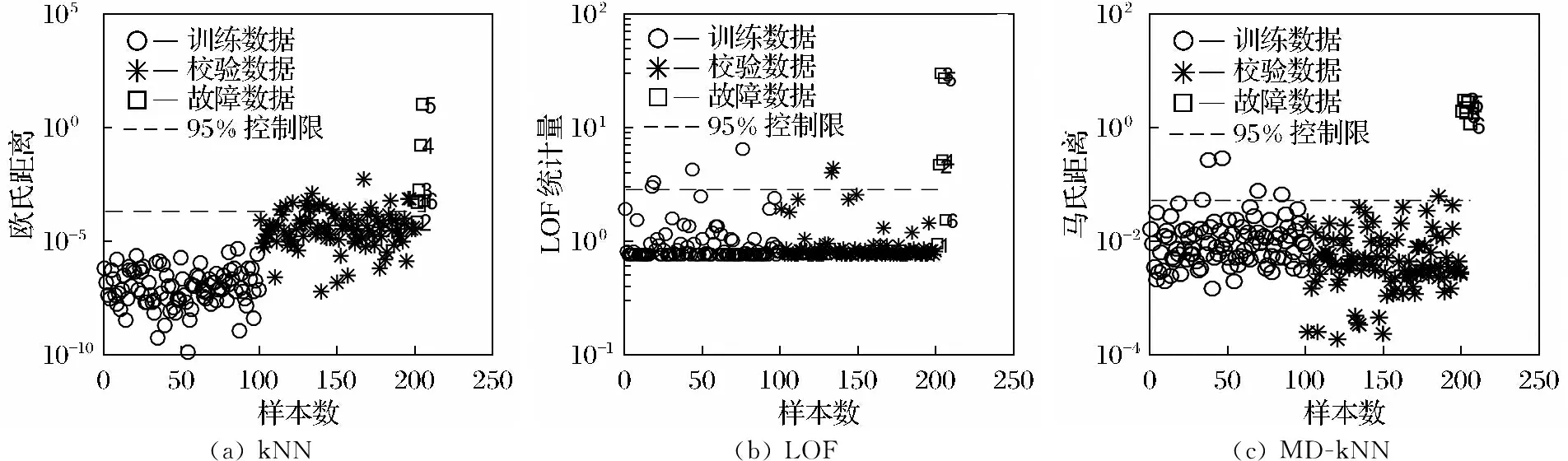
kNN、LOF和MD -kNN 3种方法对上述多模态数值例子的检测结果如图6和表1所示。其中kNN的近邻数k取3;LOF的近邻数取23。观察图6可以得出,MD -kNN检测出的故障最多,误报个数最少,MD -kNN的算法更为可靠。

表1 多模态数值例子的检测结果对比Table 1 Comparison of detection results of multimodal numerical example %

(a) kNN(b) LOF(c) MD-kNN

根据表1可得出,MD -kNN算法较kNN和LOF有显著优势。LOF算法易被离群样本影响的特性导致其漏报个数较多。相较于kNN和LOF 2种算法,MD -kNN较少发生误报和漏报的现象,说明此算法具有更优的特性。

2.2 半导体生产过程数据

半导体的生产过程是实际的工业过程例子,已广泛应用于利用数据驱动进行故障检测的领域中。本文结合半导体工业的实际例子,即以A1堆腐蚀工业过程为例[10-12],对前面提及的故障检测方法进行对比。该数据是由3个模态的107个正常批次和20个故障批次组成,每个模态分别选取32个批次用于建模,剩下的正常批次作为校验批次用来验证模型的准确性,因此建模批次为96个,正常校验批次为11个,故障批次为20个。在21个测量变量中筛选17个作为检测变量数据,选取的变量见表2,关于半导体的数据取自文献[10-12]。

表2 半导体生产过程所用变量Table 2 Variables used in semiconductor production process

本文采取最短长度的方法获取等长批次。 消去初始状态的5个不稳定样本, 储存85个样本来适应最短的批次。 把三维建模信息X根据每一个批次所在的方向进行展开, 最终变成二维矩阵X。 该方式同样用于数据的校验和故障处理。 对于二维矩阵, 依次采取kNN、LOF以及MD -kNN 3种方法来完成建模, 将其应用于11个校验批次, 以及20个故障批次, 完成故障检测。 对于kNN方法, 近邻数值k取3; 对于LOF方法, 带宽取值为0.01, 近邻数值取8。 kNN、LOF以及MD -kNN 3种检测方法的具体检测结果见图7, 其中虚线表示各统计量95%的控制限。 从图7可以得出: kNN检测出所有校验数据, 故障数据只检测出16个; LOF检测出全部校验数据, 而故障数据仅检测出13个; MD -kNN则检测出所有校验数据和故障数据。 相较于kNN和LOF算法, MD -kNN算法的检测可靠性最高, 证明了MD -kNN算法对于多模态间歇过程故障检测的优越性。

在3种算法中,MD -kNN算法不仅误报率为零,漏报率也最低,具体数据见表3。

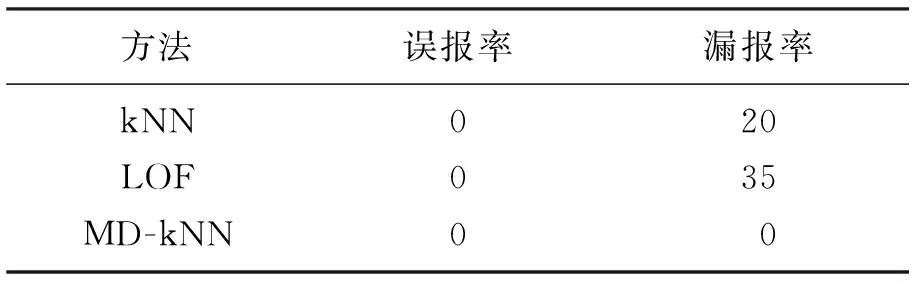
表3 半导体过程的检测结果对比Table 3 Comparison ofdetection results of semiconductor process %

3 结 论

本文研究了以kNN算法为基础的适用于多模态过程故障检测的新算法,该算法采用计算样本间马氏距离的方法消除模态间的方差差异,能够最大程度上分离多模态的正常和故障数据,使得检测的故障数据更准确。相较于传统的故障检测算法,本文算法应用在数值例子和实际的半导体工业数据上,可以有效减小误报率和漏报率。