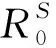具有非线性干扰的随机SIR模型的平稳分布和灭绝性
刘明鼎, 张艳敏
(青岛城市学院 理学院, 山东 青岛 266106)
传染病是在世界范围内对人类健康构成重大威胁的疾病。其中乙型肝炎病毒(HBV)已经造成了全世界20亿人的感染和近百万人的死亡[1]。HBV在人类之间的传播途径比较复杂,例如可以通过母婴、血液和性接触等途径进行传播[2]。而原发性肝癌患者80%是因为感染了HBV而引起的[3]。由此可见HBV对人类的公共卫生健康造成了巨大的威胁。疫苗是控制各种传染病传播的有效手段之一,而通过构建数学模型研究这些传染病的传播动力学行为也是控制传染病传播的有效方式,也有了较为丰富的研究成果[4-9]。这些数学模型可以从更广泛的角度去理解、分析传染病的传播行为。因此部分学者通过建立数学模型研究HBV的传播,解释传播过程中的动力学行为[1,5,10-12]。文献[1]研究了如下确定性的HBV传播模型:
(1)
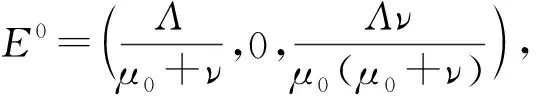
然而在现实世界中,传染病的传播会受到环境噪声的影响。因此研究随机传染病模型的动力学行为比较符合实际情况,对分析病毒在自然环境中的传播行为更有帮助。其中大多数随机传染病模型研究的是线性扰动[13-16]。普遍具有形式dX(t)=[Λ-βX(t)-G(t)X(t)]dt+ηX(t)dB(t),其中η2>0为一维标准布朗运动B(t)的干扰强度。为了深入了解HBV传播的动力学行为,研究具有非线性扰动的随机传染病模型是非常有意义的。因为与线性扰动相比,非线性扰动更能反映真实情况。已经有部分学者开始研究具有非线性扰动的传染病模型。Liu等[17]和Han等[18]研究了二阶扰动的随机传染病模型,具有
dX(t)=[Λ-βX(t)-G(t)X(t)]dt+ηX(σ11+σ12X(t))dB(t)
的形式。KHAN等[12]研究了如下非线性扰动的随机乙型肝炎传播模型,
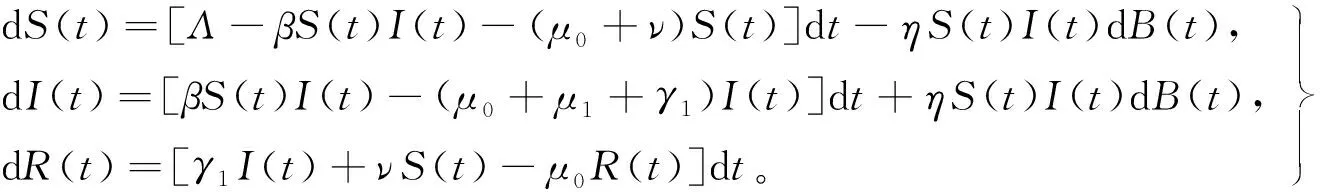
(2)
证明了模型(2)的正解全局唯一性、持久性以及灭绝性,但并没有证明其存在稳定的正平衡态或者存在平稳分布。而正平衡态的稳定性是生物数学模型动力学性质的重要研究内容。然而,大多数随机模型没有传统的正平衡态。因此,随机生物数学模型的平稳分布(随机正平衡态)一直受到广泛关注。
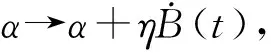
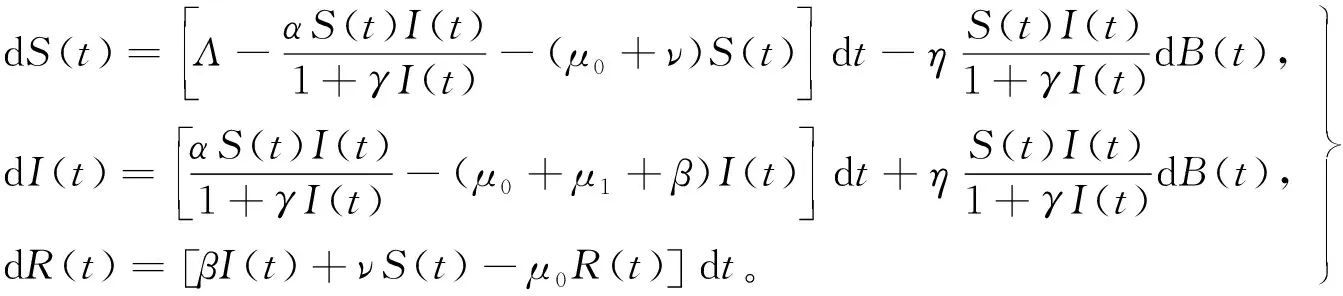
(3)
本文将首先研究模型(3)正解全局唯一性,然后依次给出其存在平稳分布和灭绝性的充分条件。因为模型(3)具有的是非线性扰动,所以对其存在平稳分布的证明需要构造新颖的Lyapunov函数,需要采用新的证明方法。
1 预备知识
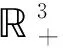
定义1[19]对于n维随机微分方程dX(t)=f(X(t),t)dt+g(X(t),t)dW(t)所描述的马尔科夫过程X(t),(t≥t0),具有初值X(0)=X0,W(t)是n维标准布朗运动。则关于随机微分方程的一个重要算子定义为
例如,设二阶可微函数V,则有
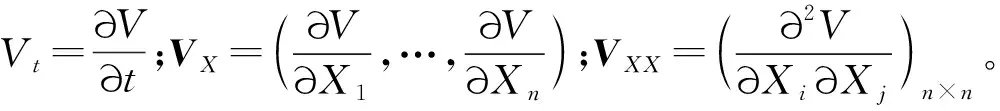
dV(X(t),t)=LV(X(t),t)dt+VX(X(t),t)g(X(t),t)dW(t)。
设X(t)为d维欧式空间Ed上的齐次马尔科夫过程,且满足
扩散矩阵为
引理1[20]设X(t)为马尔科夫过程,如果存在有界开区域D∈Ed,Γ为区域D的正则化边界,并满足以下条件:
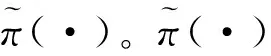
其中g(x)为可积函数。
引理2
(a+b)2=a2+2ab+b2≤2(a2+b2),(a≥0,b≥0)。
引理3[21](强大数定律) 设M={M}t≥0在t=0处满足实值连续局部鞅消失,则有
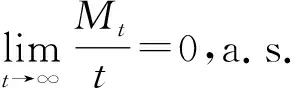
2 全局正解存在唯一性
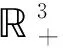
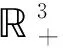
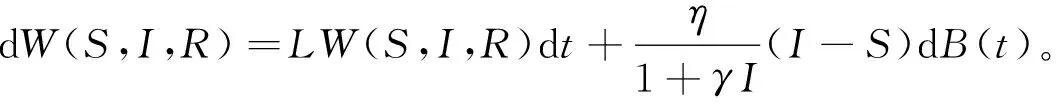
(4)
当x>0时,x-1-lnx>0,因此可以构造非负函数
W(S,I,R)=(S-1-lnS)+(I-1-lnI)+(R-1-lnR)。
则有
则有
至此完成了LW≤K的证明。接下来证明τe=∞的过程是标准的,同文献[11-16]几乎完全一致,这里略去。定理1证毕。
3 平稳分布
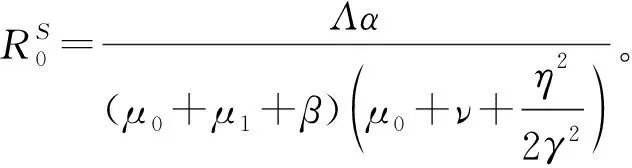
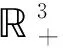
证明 根据引理1结论,为了保证定理2成立,需要满足引理1的2个条件。而条件1)的证明与文献[11-16]完全类似,比较容易得到,所以这里省略。主要工作是验证条件2)。接下来证明条件2)成立,首先定义如下4个随机Lyapunov函数:
其中C1,M为常数,在后面的计算中会给出具体满足的关系式。
第1步 对V1(S(t),I(t))使用It公式,并利用引理2得
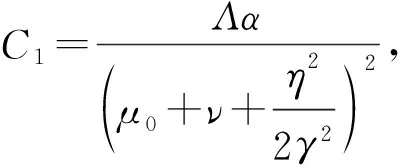
第2步 对V2(S(t),I(t),R(t))使用It公式,注意到1 第3步 对V3(R(t))使用It公式得 第4步 对V(S(t),I(t),R(t))=MV1+V2+V3使用It公式得 式中 第5步 记ε>0是充分小正数, 其中 记 同时取M、ε满足下列各式: 为了清晰证明过程,定义 证明 第1步,对式(3)的前2个方程在(0,t)上进行积分得 将式(12)与式(13)相加得 (14) 在式(14)两端从(0,t)积分可以得 在式(16)两端从(0,t)上进行积分,并结合引理3、式(15)可以得到 则当定理条件R0<1成立时,有 我们将使用表1中的模型(3)系数取值,通过数值算例来验证文章的结论。 表1 模型(3)系数取值Table 1 Parametric values of model (3) 利用文献[25]提出的高阶法,对模型(3)进行离散,得到离散方程 (17) 对于具有非线性扰动的随机HBV传染病模型,本文利用随机Lyapunov分析法,以及It公式,得到了以下结论: 2) 因为模型具有非线性扰动,所以构造了新颖Lyapunov函数,证明过程也更具挑战性。文中所构造的Lyapunov函数的方式以及证明过程简化有效,可以推广到类似模型的证明中。 3) 通过数值算例对平稳分布和灭绝性的条件进行了验证。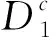
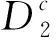
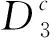
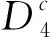
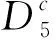
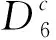
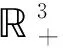
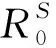
4 灭绝性
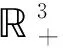
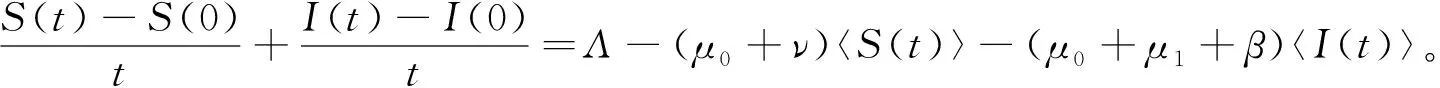
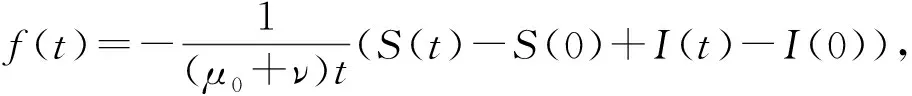
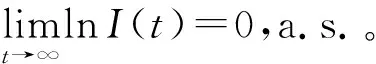
5 数值算例

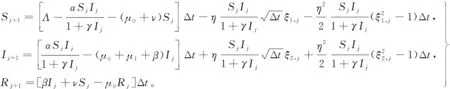
6 结 论