基于K-prototype聚类的学生教育画像分析

翟 鸣 宇， 程 建, 王 苏 桐, 王 延 章

(大连理工大学 经济管理学院, 辽宁 大连 116024)

一、引 言

随着数字化校园的建设，高校积累了大量学生基本信息、生活消费、学习读书等动静态数据。《中国教育现代化2035》[1]中指出，各大高校应结合大数据、人工智能技术，积极打造“智慧校园”，通过学生画像，建立学生标签，采取个性化的教学方式等全方位了解学生、引导学生，从而提高教学质量，培养优秀人才[2]。

学生画像是利用用户画像技术，围绕学生在学习、生活、个人发展、社会交往等多个角度产生的行为数据进行加工，为学生定义个体或群体画像，为学生自我评价、自我诊断与改进提供有效的量化参考；同时，也为学校学生管理提供学生个体及群体的直观且精确的描述，从而为日常管理、制度建设、教学管理等事务提供有效的运行支撑。学生画像的数据主要来源于包括性别、专业等基本信息的静态数据，以及包括食堂消费、网络行为等动态数据，这些数据可以从多个维度刻画学生的形象，通过聚类方法构建具有明显标签化的学生特征，可以更加科学地对学生进行分类管理。学生群体的画像特点在数据处理之前通常是未知的和杂乱的，运用监督机器学习方法难以处理，通常采用以聚类为代表的无监督机器学习技术。

随着校园信息化建设的推进及大数据分析技术的成熟，国内外学者纷纷展开了关于学生教育画像方面的研究。国外在这方面的研究起步较早但是更偏向于在线学习者的肖像构建、学生学习风格分类、协同学习与预测学生表现等。Antonenko和Velmurugan[3]通过层次聚类方法Wards聚类和非层次聚类方法k-Means聚类，分析在线学习者的行为模式。Dharmarajan和Velmurugan[4]基于2228名学生的成绩记录，使用CHAID分类算法从学生以往成绩中挖掘信息并预测学生的未来表现。Manikandan等人[5]使用k-Means聚类方法将具有相同学习能力的学生聚类并构建特征。Tian等人[6]基于西安交通大学的学生数据集，运用模糊C均值聚类方法构建在线学习肖像库，为不同学习肖像的使用者提供个性化在线学习环境。这些方法虽然取得了较好的聚类效果，但是数据层面只考虑了学生成绩因素，缺少对学生生活、消费、网络数据的考虑与探究。

国内这方面的研究虽然起步较晚，但结合校园各类信息数据，研究方向更为广阔。武书舟[7]分析学生静态数据与动态数据，根据不同类别数据特征提取结果，对不同群体学生建立学生画像标签体系，从而进一步建立学生画像，并基于模糊综合评价算法和学生画像的家庭经济困难认定模型，科学地给出高校学生家庭经济情况认定结果。万安庆[8]利用学生成绩、体测数据、一卡通刷卡数据、无线网络使用数据，构建包含学生学习情况、经济水平、生活轨迹、人际关系、网络使用习惯的亚健康画像。董潇潇[9]以高校各种校园数据为基础，构建大学生行为画像，从多个维度和角度综合描述了大学生在校信息状态，并通过数据挖掘技术，对大学生行为画像进行聚类分析，挖掘大学生的学习及生活上潜在的规律及模式，在一定程度上为教学部门提供了决策支持信息。杨浩[10]获取了10 022名学生的学习、消费、论坛数据，并根据数据模型和系统需求构建了学生画像标签体系。根据系统的功能需求和标签体系，运用多种机器学习方法对学生数据进行分析。使用模拟退火算法优化的模糊C均值算法，对学生的学习和消费水平进行分析，使用文本分析算法分析学生的兴趣爱好、关注话题和情绪指数，基于支持向量机算法对学生的挂科情况进行预测，选择Apriori算法预测学生具有挂科风险的科目，选择C4.5决策树算法对学生生活、学习以及情绪异常进行分析，对学生的学籍异动情况进行预警。经过系统的验证和测试，优化后的模糊C均值算法的聚类效果显著提高，挂科预警的准确率达到83%，用于学生挂科科目预警的关联规则最高置信度为73%。然而以上这些方法虽然考虑了学生校园生活数据，但是这些方法仅通过一些描述统计信息去表示学生画像，缺少可视化的效果，且在聚类过程中，将类别特征直接通过编码转换为数值特征，在距离计算上会导致较大误差，聚类效果有待提升。

传统 k-mean算法仅限于数值数据。Ahmad和Dey[11]提出了一种基于k-prototype的聚类算法，该算法适用于具有混合数值和类别特征的数据，通过新的成本函数和距离度量，克服了k均值仅支持数值特征的局限并提供了更好的聚类特征。针对高校教育大数据中的类别数据与数值数据，本文分别采用汉明距离与欧式距离的方式进行混合度量，基于K-prototype进行聚类，根据聚类的描述统计结果，形成学生特征标签，采用词云图可视化的方式构建学生教育画像，为高校管理人员的科学管理提供决策支持。

二、基于K-prototype的聚类模型

聚类是一种探索类簇间相关性并评估簇内数据相似性的无监督机器学习方法。

本文基于K-prototype对高校学生大数据进行聚类，并在聚类的基础上构建学生画像，模型整体框架如图1所示。学生数据中既包含如性别、生源地等类别型特征，又包含年龄、回寝时间等数值型特征。目前流行的聚类方法如K-means、分层聚类、密度聚类等，只能处理数值型特征，本文运用的教育大数据含有大量的类别特征，部分特征类别较多，运用此类方法通常会导致聚类效果较差。

K-modes算法是在数据挖掘中对类别特征型数据采用的聚类算法，是对K-means算法的扩展。它按照K-means的核心内容进行修改，针对类别属性的度量和聚类中心的计算进行改进，以类别特征属性值的个数作为聚类中心间的距离，但只能处理类别型特征数据。因此需要有一种能同时处理两种不同类型数据的聚类方法。K-prototype算法[11]继承了K-means算法和K-modes算法的思想，并加入了描述数据簇的原型和混合属性数据之间的相异度计算公式，是处理混合属性聚类的典型算法。

图1 基于K-prototype学生聚类框架

1.距离度量

K-prototype分别按照K-means和K-modes的距离计算方法欧式距离和汉明距离来度量数值型特征和类别型特征，将其进行组合来构成对原型的距离。假设样本为n个，特征为m个的集合D={X1,X2,…,Xn},Xi,Xj分别表示两个样本。

对于数值型特征，首先需要进行规范化处理，将其映射到[0,1]区间，再计算数值特征的距离，K-means使用的欧式距离源自欧式空间中两点间距离公式，距离表示为：

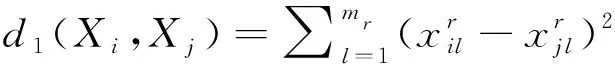
(1)

对于类别型特征，K-modes使用汉明距离进行计算：

(2)

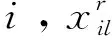
计算混合特征类型的对象之间的相异性可以把不同的特征组合到单个相异性矩阵中，设k为聚类个数，Qc={qc1,qc2,…,qcm}表示类别c选择的类别中心，因此，数据和中心簇的距离可表示如下：

d(Xi,Qj)=d1(Xi,Qj)+γld2(Xi,Qj)

(3)

则K-prototype的损失函数可以定义为：

(4)

2.混合聚类K-prototype

数值变量经过标准化，方差为1，因此，γc设置为0.5。K-prototypes算法具体步骤：

步骤1：从数据集D中随机选择k个初始聚类中心{c1,c2,…,ck}；

步骤2：遍历数据集D，根据公式(3)计算样本与各个聚类中心的距离，将该样本分配到距离中心最近的类别中；

步骤3：每次分配样本后，更新数值特征与类别特征的聚类中心。对于数值特征采用公式(1)计算，对于类别特征采用公式(2)计算；

步骤4：采用公式(3)和(4)计算损失函数；

步骤5：如果新的损失函数值小于所设定的阈值或迭代次数大于设定的T，则计算结束，输出聚类中心，否则重复步骤2、3、4。

3.聚类特征分析及画像构建

聚簇个数的选定，关系到不同聚簇得到统计特征及画像情况，轮廓系数(Silhouette Coefficient)[12]结合了内聚度和分离度，可以客观地评价聚类效果的好坏，因此，在通过设置不同的聚簇个数，从中选择轮廓系数表现最好的聚簇。

形成聚簇之后，对每个聚簇的中心进行描述，对于数值特征，计算该聚簇学生群体的均值、方差，从基本属性、生活规律、日常消费3个维度进行评价，并在聚簇中按照必修课平均成绩进行进一步细粒度划分，使这些聚簇的画像构建更加全面具体。

三、基于教育大数据的学生聚类分析

1.数据预处理

本文使用辽宁省某高校的学生脱敏数据进行分析，该数据集包含了辽宁省某高校大学生基本信息、学籍信息等静态数据，以及2018～2019年的成绩数据、图书借阅数据、一卡通生活消费数据、奖惩贷记录、上网记录、门禁记录等动态数据。

数据预处理在数据挖掘中约占整个工作量的80%，数据的质量将会直接影响模型预测的效果[13-14]，因此，在建模分析之前，需要先对数据进行预处理。数据预处理前有2017级学生4695名，处理之后为4624名。

为了提升数据质量，针对一卡通消费记录及网络信息记录不完全、成绩信息及基本信息存在缺失的样本进行删除操作，K-prototype算法针对数值型数据采用欧式距离作为度量，必修课加权成绩、月均借书数量等特征的量纲之间存在较大差异，采用最大最小规范化来减少不同量纲对聚类结果造成的影响。对每个样本的数值属性使用如下公式进行规范化。

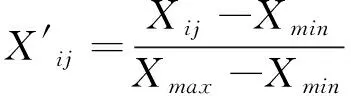
(5)

其中，X′ij表示该属性归一化后的值，Xij表示未归一化的值，Xmax表示该属性所有样本最大值，Xmin表示该属性所有样本最小值。

2.数据描述

为经过数据预处理之后的数据类型汇总，分为学生基本信息、消费信息、教务信息3个部分，基本信息包括学生背景信息、党员发展阶段等属性；消费信息主要由一卡通消费以及与一卡通绑定的IP入网账户的消费按照时间维度汇总而成；教务信息包含学生挂科门数、必修课加权平均分数,预处理后的2017级学生类别特征和学生数值特征如表1和表2所示。表1中还包括院系、班级、考生类别、生源地、宿舍、贷款金额、资助等级、资助金额共18个特征，由于每个特征的取值较多，故仅列出部分特征值。

表1 2017级学生类别特征

表2共包含27个特征,思政课程包含马克思主义基本原理、中国特色社会主义理论与实践等课程，体育课程包含羽毛球、足球、擒拿格斗等课程。在生活消费数据方面，受数据收集渠道限制，本文只能获取学生基于校园卡的消费，若在学校周边的其他商户消费，则无法获得，因此，月均食堂午餐次数等特征数据只能代表学生在学校食堂消费的次数,月均夜间上网在线时长表示23：00～6：00校园网在线时长。

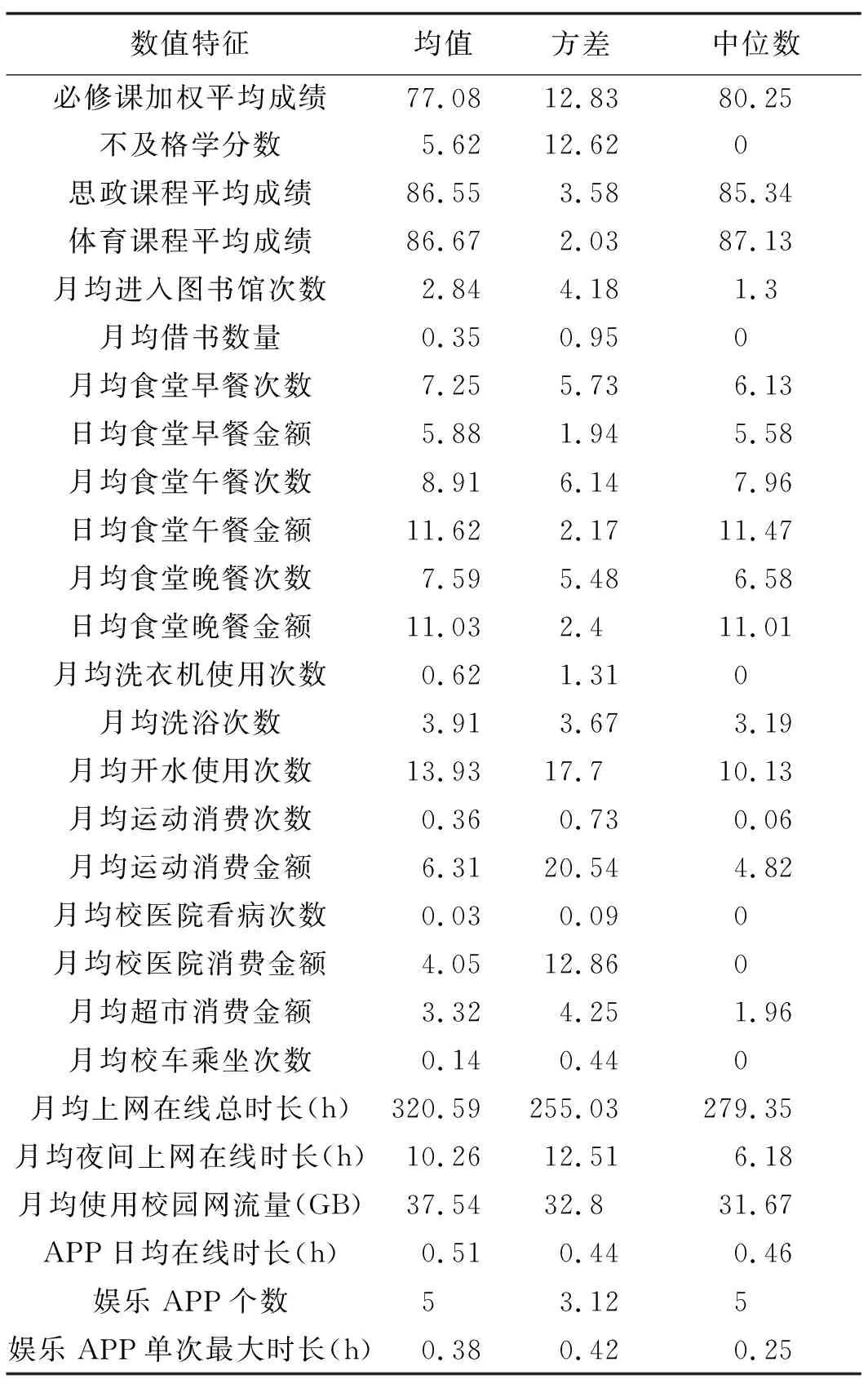
表2 2017级学生数值特征

3.聚类评价

本文学生聚簇的划分个数K通过轮廓系数(Silhouette Coefficient)来进行选取。其结合了聚类的凝聚度(Cohesion)和分离度(Separation)，用于评估聚类效果的好坏。轮廓系数的定义公式为：

(6)

其中，ai表示第i个样本与其同一簇群中所有其他数据之间的平均距离，即为量化簇内的凝聚度。bi表示其与最近一个聚簇的平均距离，用于量化簇内的分离度。s为全部样本的轮廓系数平均值。不难发现，若s小于0，说明s与其簇内元素的平均距离大于最近的其他簇，表示聚类效果不好；如果ai趋于0，或者bi大于ai，那么s趋近于1，说明聚类效果最好。

本文对2017级学生的数据进行聚类分析。首先，我们用轮廓系数对K-prototype聚类方法的性能进行分析，并与K-Means、DBSCAN方法进行比较(K-Means模型中只使用数值型数据，DBSCAN采用不同聚类半径下最优值)，比较如图2所示。

从图2中可以看出，本文所提方法K-prototype明显优于其他常用聚类方法K-Means与DBSCAN，体现出针对同时包含类别特征和数值特征的数据时，K-prototype聚类更加具有优势。当聚类个数K=4时，此时聚类效果最好。本文以K-prototype聚类方法按照K=4进行聚类，得到A、B、C、D4个聚簇，对其人数比例、学年必修课加权成绩进行统计分析得到表3。其中，成绩优秀代表学年必修课加权平均成绩大于85分，成绩差代表学年必修课加权平均成绩小于60分。

图2 轮廓系数对比图

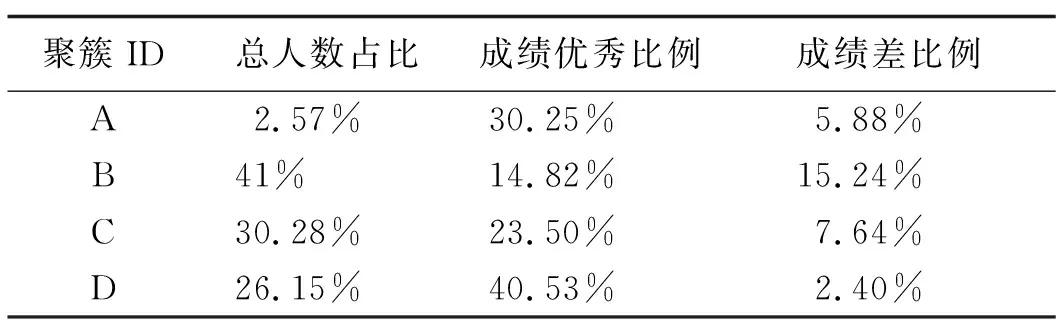
表3 教育画像聚类结果

表3展示了教育画像的聚类结果，ABCD这4个类别人数比例、成绩优异与较差的比例皆不相同，从图3可以看到B类男生最多，A类入党志愿比例最高，D类获奖学金比例最高、家庭困难比例也最高。

图3 4类群体基础信息对比

稳定性表示数据的方差，方差越小，稳定性越高。从图4中可以发现，B类学生早餐花费最高；D类学生早餐花费稳定性最好，早餐次数最多；C类学生早餐次数稳定性最好；D类学生超市花费最多；A类学生超市花费稳定性最好。

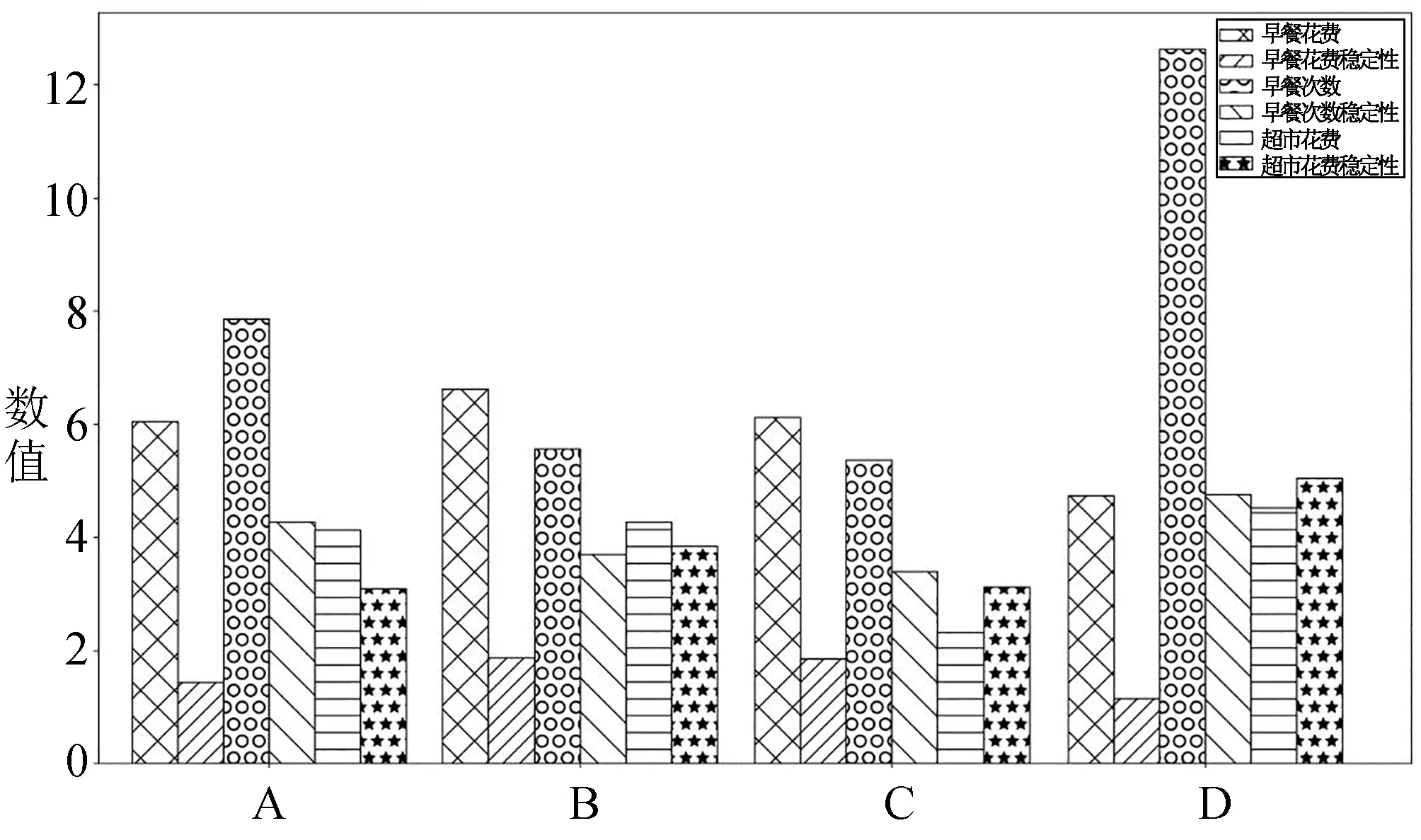
图4 4类群体早餐及超市消费情况对比

四、基于数据挖掘的学生行为画像分析

本文基于辽宁省某高校教育大数据进行K-prototype聚类，在对学生群体特征标签进行标注后，对各类学生群体进行详细分析。

1.学生画像分析

构建学生群体画像是以形象化的形式对学生群体的特点进行刻画，本文在基于K-prototype聚类的基础上，对学生群体画像进行分析与刻画。为了纵向比较2017级学生的特征，本文提取了每位学生分数排在前3的课程名称，并与2018级、2016级、2015级学生对比,学生的加权成绩反映了学生对课程的重视程度，图5所画的词云图反映了2017级学生所重视与关注的课程与其他年级学生的差异情况。

如图5所示，2017学生处于大学二年级，较为重视思政课的学习。此外，材料力学、英语、大学物理等基础性课程投入精力较多。从(a)～(d)4幅词云图可以发现，随着年级的升高，课程的重心也在发生着变化。在大一时间段内学生的主要精力都放在学分较高、难度较大的基础学科上，因此，在高等数学、数学分析、程序设计等基础学科的加权分数较高。随着年级的升高，思想政治教育理论课得到进一步加强，大二阶段着重开展中国特色社会主义等政治理论课的学习。大三阶段集中开展各类专业课的学习，不同学院、不同专业差异较大，因此，课程覆盖范围广，课程门类较多，同时开展实习、实训类课程。大四的学生面临毕业，则把精力更多地集中在了毕业设计和毕业论文。

图5 各年级学生加权成绩排名前3课程词云图

根据轮廓系数实验结果，运用K-prototype以K=4对2017级学生数据进行聚类，根据聚类结果分别从类别特征和数值特征两个维度构建学生画像，如表4～7所示。其中，数值型特征以表格的形式进行展现，从基本属性、日常消费、生活规律3个维度进行刻画，除了基本属性之外，均采用均值±方差的方式进行表述，平均成绩为学生必修课平均成绩。在校的消费金额均为日均，消费频次为月均。

基于聚类结果，对4类学生群体构建画像。对于数值型特征，按照必修课平均成绩大于85分为优秀、小于60分为差进行细粒度划分，对于数值特征分别进行统计。此外，男女生比例表示聚类中的男生人数与女生人数之比，数值大于1，表示男生人数大于女生人数，反之表示男生人数小于女生人数；入党意愿比例表示入党申请人、积极分子、发展对象占总人数的比例，获奖比例表示获得奖学金的学生占总人数的比例，困难比例表示家庭一般困难及特别困难占总人数的比例。将学生聚类群体各类特征的均值与方差相互进行比较分析，同时与表2的2017级学生整体数值特征进行比较，可以分析各类学生群体的特征并对其进行定义。为了更好地对不同学生进行聚类，将必修课加权平均成绩、思政课成绩和入党意愿作为“思想积极型学生”的判断指标；将娱乐App个数、夜间上网时长作为“夜猫子游戏型学生”的判断指标；将到餐厅就餐次数和夜间上网时长作为“生活规律性型学生”的判断指标；将获得奖学金的比例、家庭困境比例和成绩优秀学生比例作为“节俭好学型学生”的判断指标。从表4～7中，ABCD这4个类别的学生群体画像，可以总结出如下规律：

表4中，A类学生群体有119人，以经管学院、软件学院为代表，该类别在整体中人数较少，必修课加权平均成绩为79.02分，在4类群体中排名第二且高于2017级整体学生必修课加权平均成绩77.08分。其中，男女生比例较低，仅为0.78，表示男生人数少于女生，在4个学生群体中女生人数最多；思政课平均成绩较高；入党意愿比例为0.52，在4个群体中最高；获奖学金比例较高，为0.32；日常消费的频率与额度居中；困难比例低于D类群体，高于B、C类群体。早餐食堂就餐次数与其他4类学生相比较高，具有早起的习惯，而午餐晚餐频率低于整体均值，洗浴次数低于整体均值，夜间上网在线时长略高于整体均值，使用娱乐APP个数处于中间水平，月均上网在线总时长低于整体。获得奖学金比例高表明，该类学生群体成绩较为优异，在学生学习、日常活动中表现活跃，其中成绩优异的学生比例较高，为30.25%。成绩优秀的学生中女生较多，入党意愿强烈，该类学生拥有较好的生活作息和学习习惯，因此可以将A类学生标记为“思想积极型学生”。

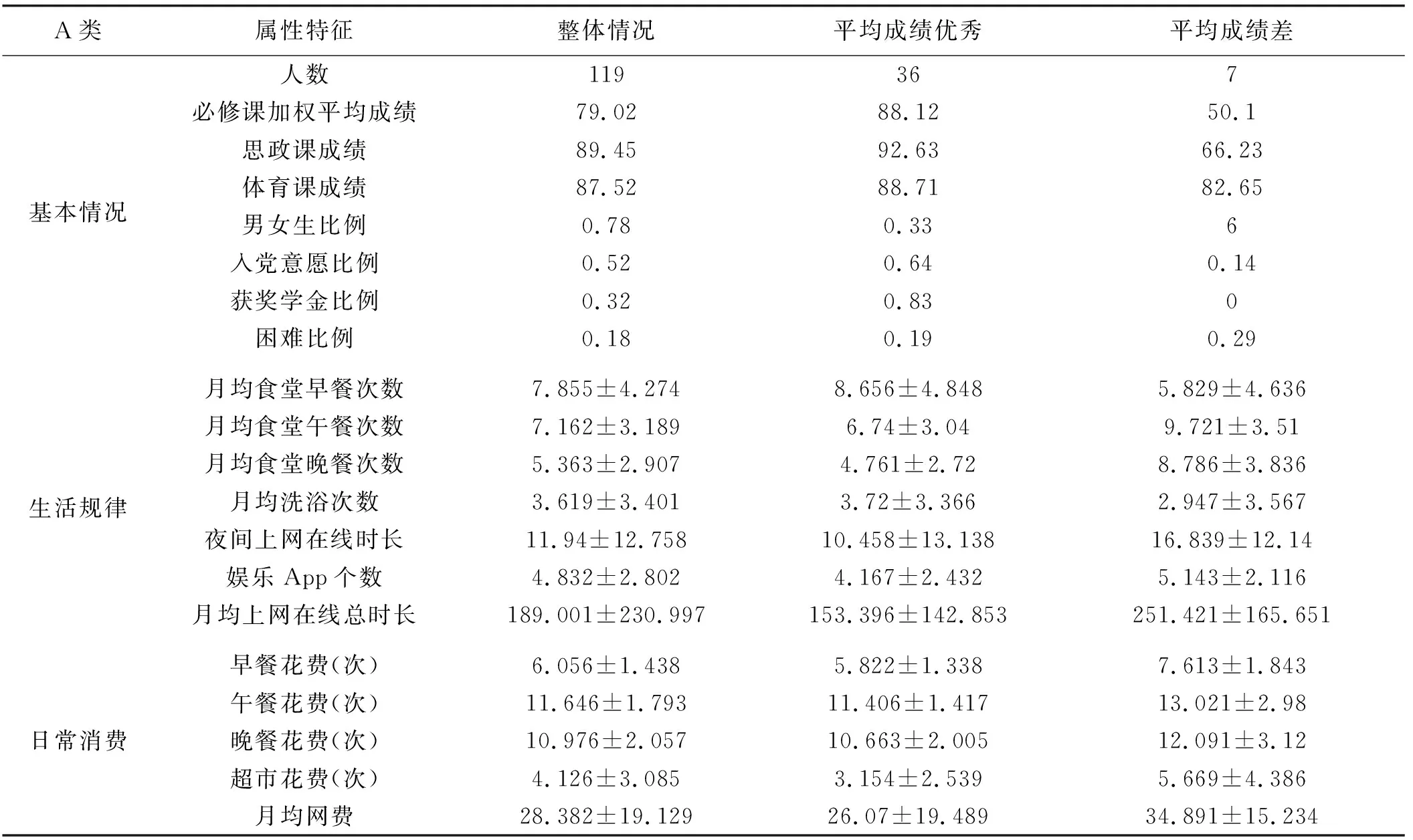
表4 A类学生教育画像

从上述画像特征可以看出，“思想积极型学生”的比例较低，但对学习成绩要求较高、入党积极、思想要求进步，善于运用网络媒介的优势，发挥其对学习的正向积极作用；性别在这种类型中具有非对称性；日常生活较为规律，在日常花费上较为合理。

表5中，B类学生群体有1896人，必修课加权平均成绩为73.11分，在4类学生群体中最低；思政课与体育课成绩偏低，平均成绩优秀的学生比例在4类群体中最小(14.82%)，成绩差的学生比例最大(15.24%)。在4类学生群体中，B类学生男生占比最大，男女比例为5.18:1，获奖学金比例(12%)最小，家庭贫困比例(17%)较小，月均网费最高，为59.717元，学校食堂就餐次数最少，夜间上网时长最多，为每月17.321小时，远高于整体均值10.26小时，相较于其他学生群体，娱乐App数量较大且上网娱乐时间最长，夜间上网时长较高，因此将B类学生标记为“夜猫子游戏型学生”。从上述画像特征可以看出，“夜猫子游戏型学生”占比较大，对学业较为忽视；家庭较为优越，上网花费较高，上网时长尤其是夜间上网时长最长，生活作息不规律，可见网络对学生的负向影响较大。对此，可以将这类学生列为重点关注学生群体，特别是该群体中平均成绩较差的同学，对其进行学业预警，开展大学生涯规划、职业规划等讲座，引导其形成良好的学习和生活习惯。

表5 B类学生教育画像

表6中，C类学生群体有1400人，必修课加权平均成绩为77.02分，思政课与体育课成绩居于中间水平，成绩优秀学生比例(23.50%)较高，成绩差学生比例(7.64%)较低，作息时间规律，早餐就餐次数较少，夜间上网时长最短，生活习惯较好，因此可以将C类学生标记为“规律作息型学生”。

表6 C类学生教育画像

从上述画像特征可以看出，“规律作息型学生”代表了学生群体中的大多数，学业要求不高，思想上中规中矩，对人生规划缺少思考。因此，应对此类学生加强引导，帮助学生做好人生规划。

表7中，D类学生群体有1209人，必修课加权平均成绩为81.86分，在所有类别中，成绩优秀学生比例最高，为40.53%；思政课与体育课成绩最好，且获奖学金比例最高；该学生群体中家庭困难比例最高，为0.34；在4类学生群体中，在学校食堂就餐平均次数最高，花费最低。这体现出该类学生生活较为节俭，因此可以将D类学生标记为“节俭好学型学生”。

表7 D类学生教育画像

从上述画像特征可以看出，“节俭好学型学生”家庭困难程度在同辈群体中最大，但对自身学业的要求却没有降低；作息时间规律，花费均控制在日常的必备花销上。因此，这类群体可以作为同辈的学习典范。同时，也要重点关注一些成绩较差的学生，可能会因家庭贫困造成对学业的影响。对该类学生应重点关注其家庭情况，辅导员应主动进行关怀，为其提供勤工俭学等帮扶，在励志奖学金评定方面可重点考虑该类学生群体。

五、结 语

本文基于辽宁省某高校学生成绩、网络使用情况、消费情况等数据，采用基于汉明距离与欧式距离混合度量的K-prototype方法进行聚类，通过轮廓系数对聚类效果进行评价，并与常用的K-means、DBSCAN等方法进行对比，分析结果表明基于K-prototype的聚类在教育大数据的处理上更具优势。此外，根据聚类的描述统计结果，形成学生特征标签，构建了4类学生教育画像。画像从基本属性、生活消费、生活规律维度将学生群体划分为“思想积极型学生” “夜猫子游戏型学生” “规律作息型学生” “节俭好学型学生”4类学生群体，为学生群体赋予了特征标签，可为学生教育管理者提供相应的决策支持。

针对不同学生群体，需要有针对性的管理策略。结合上述研究结论，提出如下4点建议。

(1)对于“思想积极型学生”，应该发挥其在同辈群体中的榜样作用。树立优秀的典型案例，进行宣传，营造学生学习先进、争创思想积极的氛围。同时，高校也要关注该类型中的男生，注意男生在学业和思想上的动态，对于成绩较差的男生，高校应该给予更多的学业帮助和思想辅导。

(2)对于“夜猫子游戏型学生”，应该关注游戏对学生学业和生活的负向影响。该类型的学生家庭较为优越，在游戏类的APP使用上占据了较多的时间，特别是在晚上23点后上网时间较长，会影响正常的睡眠及第二天的正常上课状态。因此，对于该类学生，高校多关注其上网的偏好及时间，对其进行合理干预和积极引导，强化体育锻炼的意识和习惯，培养正常的作息习惯。

(3)对于“规律作息型学生”，其在学生群体比例最高，需要激发该群体的学业危机意识，提前做好生涯规划。要善于运用各类资源的平台强化课程学习和实践能力的提升，提高自身价值的认知水平。

(4)对于“节俭好学型学生”，在学生家庭基本情况方面，学业危机群体中男生比例较高，应重点关注并培养此类男同学的自我管理意识。家庭贫困的学生生活习惯普遍较好，成绩也较为优异，对该类学生应重点关注其家庭情况[15]。

本文在针对不同学科专业等细粒度的挖掘分析还存在不足，未来将进一步关联消费数据及学生管理数据，提升学生教育画像的全面性，同时针对不同画像群体，制定细粒度的学业危机干预措施。