利用图像法分析水平面圆周运动临界问题

陈龙

一、水平转台

水平转台上单一物块随圆盘做匀速圆周运动是靠静摩擦力来充当向心力，而较为复杂的是绳子连两物块在圆盘上做圆周运动的临界问题.

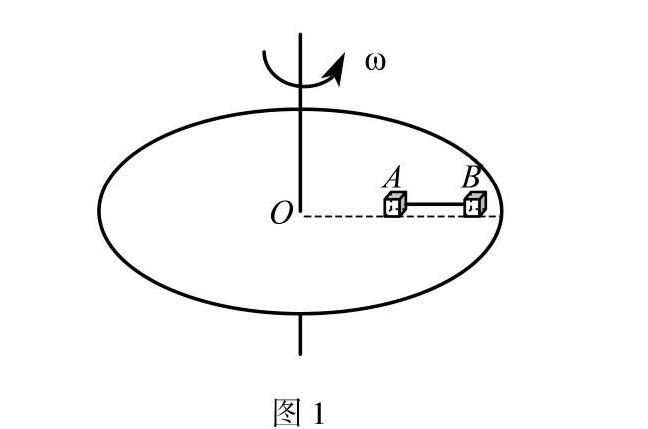
例1 如图1所示，在水平转台上有沿半径方向放置用细线相连的质量均为m的A、B两小物块（可视为质点），细线处于刚好伸直状态（未绷紧），A和B距轴心O的距离分别为R和2R，两小物块与转台间的最大静摩擦力均为重力的K倍，两物块随圆盘转动时与圆盘保持相对静止，当圆盘角速度缓慢从0增加时，试分析两小物块所受摩擦力FfA、FfB随转台角速度的平方（ω2）的变化图像.

解析 当转台的角速度比较小时，A、B物块做

图1圆周运动的向心力由静摩擦力提供， A的摩擦力为FfA=mω2R，B的摩擦力为FfB=mω22R，随着角速度增大，由上两式可知A、B物块所受的摩擦力与ω2成正比.接着继续增大角速度ω，B物块的静摩擦力先达到最大静摩擦力Kmg，此时对B分析，Kmg=

mω212R可得：ω1=Kg2R ，此时A的摩擦力为

12Kmg.

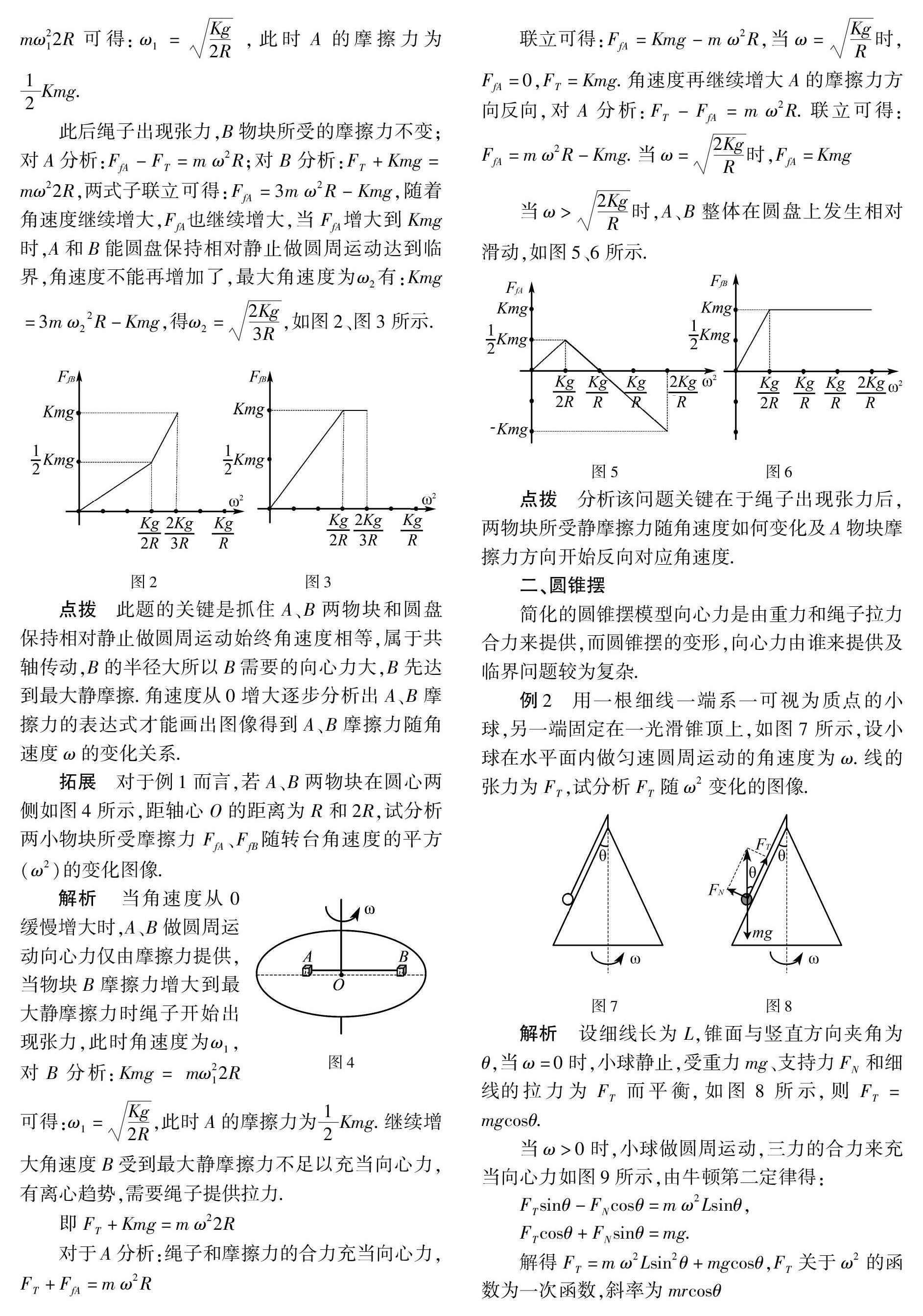
此后绳子出现张力，B物块所受的摩擦力不变;对A分析：FfA-FT=mω2R;对B分析：FT+Kmg=mω22R，两式子联立可得：FfA=3mω2R-Kmg，随着角速度继续增大，FfA也继续增大，当FfA增大到Kmg时，A和B能圆盘保持相对静止做圆周运动达到临界，角速度不能再增加了，最大角速度为ω2有：Kmg=3mω22R-Kmg，得ω2=2Kg3R，如图2、图3所示.

图2         图3

点拨 此题的关键是抓住A、B两物块和圆盘保持相对静止做圆周运动始终角速度相等，属于共轴传动，B的半径大所以B需要的向心力大，B先达到最大静摩擦.角速度从0增大逐步分析出A、B摩擦力的表达式才能画出图像得到A、B摩擦力随角速度ω的变化关系.

拓展 对于例1而言，若A、B两物块在圆心两侧如图4所示，距轴心O的距离为R和2R，试分析两小物块所受摩擦力FfA、FfB随转台角速度的平方（ω2）的变化图像.

图4

解析 当角速度从0缓慢增大时，A、B做圆周运动向心力仅由摩擦力提供，当物块B摩擦力增大到最大静摩擦力时绳子开始出现张力，此时角速度为ω1 ，对B分析：Kmg= mω212R可得：ω1=Kg2R，此时A的摩擦力为12Kmg.继续增大角速度B受到最大静摩擦力不足以充当向心力，有离心趋势，需要绳子提供拉力.

即FT+Kmg=mω22R

对于A分析：绳子和摩擦力的合力充当向心力，FT+FfA=mω2R

联立可得：FfA=Kmg-mω2R，当ω=KgR时，FfA=0，FT=Kmg.角速度再继续增大A的摩擦力方向反向，对A分析：FT-FfA=mω2R.联立可得：FfA=mω2R-Kmg.当ω=2KgR時，FfA=Kmg

当ω>2KgR时，A、B整体在圆盘上发生相对滑动，如图5、6所示.

图5         图6

点拨 分析该问题关键在于绳子出现张力后，两物块所受静摩擦力随角速度如何变化及A物块摩擦力方向开始反向对应角速度.

二、圆锥摆

简化的圆锥摆模型向心力是由重力和绳子拉力合力来提供，而圆锥摆的变形，向心力由谁来提供及临界问题较为复杂.

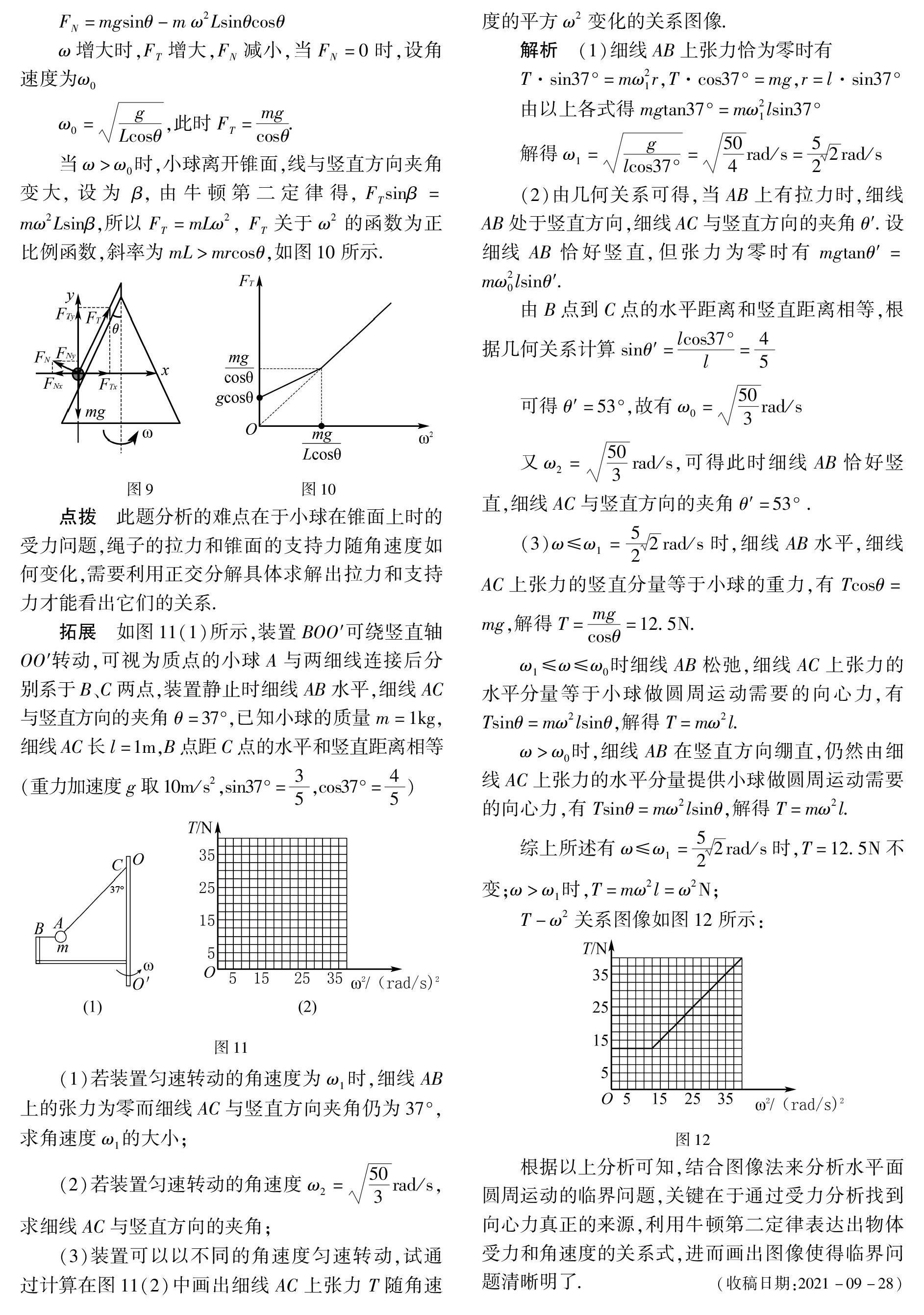
例2 用一根细线一端系一可视为质点的小球，另一端固定在一光滑锥顶上，如图7所示，设小球在水平面内做匀速圆周运动的角速度为ω.线的张力为FT，试分析FT随ω2变化的图像.

图7         图8

解析 设细线长为L，锥面与竖直方向夹角为θ，当ω=0时，小球静止，受重力mg、支持力FN和细线的拉力为FT而平衡，如图8所示，则FT=mgcosθ.

当ω>0时，小球做圆周运动，三力的合力来充当向心力如图9所示，由牛顿第二定律得：

FTsinθ-FNcosθ=mω2Lsinθ，FTcosθ+FNsinθ=mg.

解得FT=mω2Lsin2θ+mgcosθ，FT关于ω2的函数为一次函数，斜率为mrcosθ

FN=mgsinθ-mω2Lsinθcosθ

ω增大时，FT增大，FN减小，当FN=0时，设角速度为ω0

ω0=gLcosθ，此时FT=mgcosθ.

当ω>ω0时，小球离开锥面，线与竖直方向夹角变大，设为β，由牛顿第二定律得，FTsinβ=mω2Lsinβ，所以FT=mLω2， FT关于ω2的函数为正比例函数，斜率为mL>mrcosθ，如图10所示.

图9         图10

点拨 此题分析的难点在于小球在锥面上时的受力问题，绳子的拉力和锥面的支持力随角速度如何变化，需要利用正交分解具体求解出拉力和支持力才能看出它们的关系.

拓展 如图11（1）所示，装置BOO′可绕竖直轴OO′转动，可视为质点的小球A与两细线连接后分别系于B、C两点，装置静止时细线AB水平，细线AC与竖直方向的夹角θ=37°，已知小球的质量m=1kg，细线AC长l=1m，B点距C点的水平和竖直距离相等（重力加速度g取10m/s2，sin37°=35，cos37°=45）

图11

（1）若装置匀速转动的角速度为ω1时，细线AB上的张力为零而细线AC与竖直方向夹角仍为37°，求角速度ω1的大小;

（2）若装置匀速转动的角速度ω2=503rad/s，求细线AC与竖直方向的夹角;

（3）装置可以以不同的角速度匀速转动，试通过计算在图11（2）中画出细线AC上张力T随角速度的平方ω2变化的关系图像.

解析 （1）细线AB上张力恰为零时有

T·sin37°=mω21r，T·cos37°=mg，r=l·sin37°

由以上各式得mgtan37°=mω21lsin37°

解得ω1=glcos37°=504rad/s=522rad/s

（2）由几何关系可得，当AB上有拉力时，细线AB处于竖直方向，细线AC与竖直方向的夹角θ′.设细线AB恰好竖直，但张力为零时有mgtanθ′=

mω20lsinθ′.

由B点到C点的水平距离和竖直距离相等，根据几何关系计算sinθ′=lcos37°l=45

可得θ′=53°，故有ω0=503rad/s

又ω2=503rad/s，可得此时细线AB恰好竖直，细线AC与竖直方向的夹角θ′=53° .

（3）ω≤ω1=522rad/s时，细线AB水平，细线AC上张力的竖直分量等于小球的重力，有Tcosθ=mg，解得T=mgcosθ=12.5N.

ω1≤ω≤ω0时细线AB松弛，细线AC上张力的水平分量等于小球做圆周运动需要的向心力，有Tsinθ=mω2lsinθ，解得T=mω2l.

ω>ω0时，细线AB在竖直方向绷直，仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力，有Tsinθ=mω2lsinθ，解得T=mω2l.

综上所述有ω≤ω1=522rad/s时，T=12.5N不变;ω>ω1时，T=mω2l=ω2N;

T-ω2关系图像如图12所示：

图12

根据以上分析可知，结合图像法来分析水平面圆周运动的临界问题，关键在于通过受力分析找到向心力真正的来源，利用牛顿第二定律表达出物体受力和角速度的关系式，进而画出图像使得临界问题清晰明了.

（收稿日期：2021-09-28）