地震作用下斜交空心板桥支座竖向受力特性分析及其控制
梁 峰,徐庆超,阎宗尧,赵安安,王阳春,李雪红
(1.山东高速建设管理集团有限公司,山东 济南 250014;2.南京工业大学 土木工程学院,江苏 南京 211800;3.山东高速工程检测有限公司,山东 济南 250002)
伴随我国城市立体化交通的发展和交通路网的不断加密,为了克服路网周围复杂自然条件的限制,保证公路线形平顺流畅,通常会采用斜交桥、弯桥等复杂形式桥梁结构,这类桥梁具有不同于正交桥的受力性能,因此,对它们进行深入的研究具有重要的意义。空心板桥以其建筑高度小、施工方便、造价低廉等优势,得到了广泛的应用,空心板桥常用的支座为板式橡胶支座,单个支座的承载力和富余承载力都较小,而斜交桥的支座受力特点为钝角区域的反力比锐角区域的反力大,易引起支座超压或脱空[1]。在地震作用下,斜交桥的地震响应更为复杂,上部结构的惯性力是通过支座的摩擦力传递到下部结构的,支座压力越大,传递的地震剪力越大。超压的支座在地震作用下可能会被剪坏,而压力不足的支座则有可能过早地发生滑动并进一步加剧未滑动支座的剪力,因此支座不均匀受压对桥梁的抗震性能会产生较大影响。地震作用下斜交空心板桥板式支座受力的影响因素已成为人们关注的重点问题[2-21]。姚凯等[2]揭示了板式橡胶支座在不同设计参数下对斜交桥地震响应和横向抗震性能的影响;卢明奇等[3]通过分析支座剪切刚度对斜交连续梁桥自振周期的影响后认为,在支承方式一定的情况下,改变支座剪切刚度对结构的扭转振动作用不明显;Maleki[4-5]探究了跨径、桥宽、端横梁刚度等参数变化对斜交钢混组合板梁桥地震响应的影响;陈晋阳[6]以斜交连续梁桥为研究对象,选取斜交角、支座支承刚度、跨径、墩高和跨数等参数,对公路斜交连续梁桥进行了系列的地震响应参数分析;沈贤等[7]研究板式橡胶支座摩擦滑移效应以及支座动摩擦因数、剪切刚度、局部脱空等对斜交桥地震响应的影响;张培君[8]针对单跨和两跨的公路简支斜交梁桥,采用输入方向、梁端位移、支座形式等参数进行了地震作用下的动力响应分析。以上研究主要针对单联斜交结构(简支梁或连续梁)开展地震机制的研究,虽取得了一些有价值的成果,但针对地震支座受力性能的研究尚不够系统和完善,需进一步深入研究。
基于此,本文以先简支后桥面连续空心板斜交桥为研究对象,地震作用时考虑桥面连续的影响,分析支座反力的响应特性以及斜交角、盖梁刚度、跨径、桥宽等因素对支座反力分布特性的影响,并且通过调整支座竖向刚度,提出有效改善支座反力分布不均的控制措施,以期对同类公路桥梁的抗震设计提供借鉴。
1 工程概况及有限元模型
本文以京台高速公路泰安至枣庄(鲁苏界)段典型斜交桥为研究对象。该桥桥墩中心线与顺桥向轴线交角(α)为45°(桥轴线与支承线的垂线之间的锐角夹角),桥梁类型为B类,特征周期为0.4 s,场地类型为Ⅱ类,抗震烈度为7度(0.10g),跨度为16 m,主梁采用空心板(宽13 m),桥墩平均墩高为5.8 m,墩身为圆形(直径100 cm),桩身为圆形(直径120 cm)。主梁采用C50混凝土,盖梁、墩柱采用C30混凝土,桩基采用C25混凝土;支座采用板式GYZ250×52型橡胶支座。桥梁横剖面如图1所示。
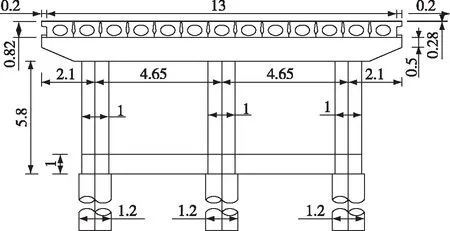
图1 桥梁横剖面示意图(m)Fig.1 Schematic diagram of cross section of bridge(m)
采用Midas/Civil软件建立桥梁有限元模型,采用梁格法,将主梁分成13片纵梁和连接纵梁的横梁,纵梁承担主梁的等效质量,而横梁通过横向截面等效成梁的横向惯性矩和扭转刚度。横向受力和变形由只提供刚度没有自重的虚拟横梁进行模拟,这能较好地反映斜交桥在恒载和活载下的纵向、横向受力特征,计算时以材料等效质量形式考虑桥面二期恒载的影响。全局坐标系X方向为桥梁起点与终点的连线方向,Y方向与X方向垂直,模型中均不考虑桩土相互作用的影响,墩底固结。有限元模型如图2所示,建立3联,每联3跨。

图2 有限元模型Fig.2 FEM model
采用反应谱法进行地震响应分析,选取《公路桥梁抗震设计细则》(JTG/T B60-01—2008)的反应谱作为地震动输入。本桥梁地处7度设防区,工程场地为Ⅱ类,其加速度反应谱如图3(图中S为加速度,T为周期,E1、E2为地震作用类型)所示。
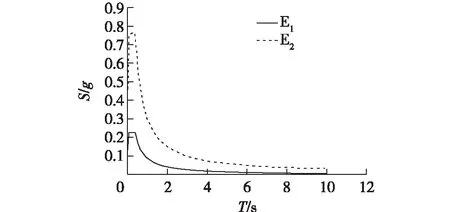
图3 在E1和E2地震作用下的水平设计加速度反应谱Fig.3 Horizontal design acceleration response spectra under E1 and E2 earthquakes
斜交桥地震响应包括水平向和竖向的地震作用,其中水平向考虑纵桥向和横桥向地震的共同作用,横桥向为沿横向墩柱中心点连线方向,纵桥向垂直于横桥向。地震动输入具体组合原则为纵桥向+横桥向+0.65×竖向。地震响应组合原则为1.0×自重效应+地震效应,其中自重包含二期恒载。空心板桥每块空心板宽1 m,每端布置两个支座,两个支座中心间距0.6 m,则桥梁每跨一侧需设26个支座。由于施工时采用先简支后连续的转换体系,则每个盖梁上需布置两排支座,笔者重点分析中间1联3跨,其支座布置如图4和5所示。
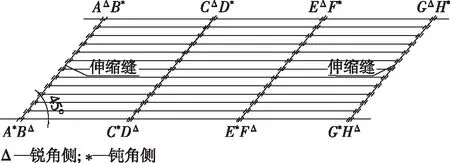
图4 桥梁支座布置(虚线为各轴线支座)Fig.4 Bridge bearing arrangement(dotted line for each axis bearings)
板式支座的竖向刚度(kv)按照式(1)计算[21]。
(1)
式中:Ev为支座等效抗压弹性模量,Ac为支座有效受压面积,tr为支座总橡胶厚度。
2 斜交桥的模态分析
通过模态分析对结构的动力特性进行研究,有助于理解结构的动力响应规律。为此,笔者首先对斜交角为0°(正交桥)、15°、30°和45°的斜交桥进行模态分析,其中,Ux和Uy分别为顺桥向和横桥向平动的质量参与系数,Rz为桥跨结构平面内扭转运动的质量参与系数(表1)。

图5 盖梁上支座布置Fig.5 Bearing arrangements on the capping beam
由表1可见:斜交角为0°时,正交桥前4阶模态形式表现为单一方向上的平动,第5阶出现平面内扭转振型。而随着斜交角逐渐增大,斜交桥第1阶模态形式表现为纵、横向平动耦合,纵向平动质量参与系数逐渐减少,由原先的92.74%减至43.61%;横向平动质量系数逐渐增大至46.58%,当斜交角为45°时,1阶模态形式出现明显的纵、横向平动耦合现象。在斜交角为15°时,第2阶则出现桥面扭转振型;当斜交角从0°增大至45°时,扭转质量参与系数从0增大到45.41%,表明当斜交桥的倾斜角度越大,地震对结构整体产生的影响就越显著,斜交桥的纵、横向平动耦合加剧,结构的扭转效应增大,同时桥面扭转振型前移。所以,对倾斜角度相对较大的斜交桥,地震计算时应考虑整体结构的空间耦联性。
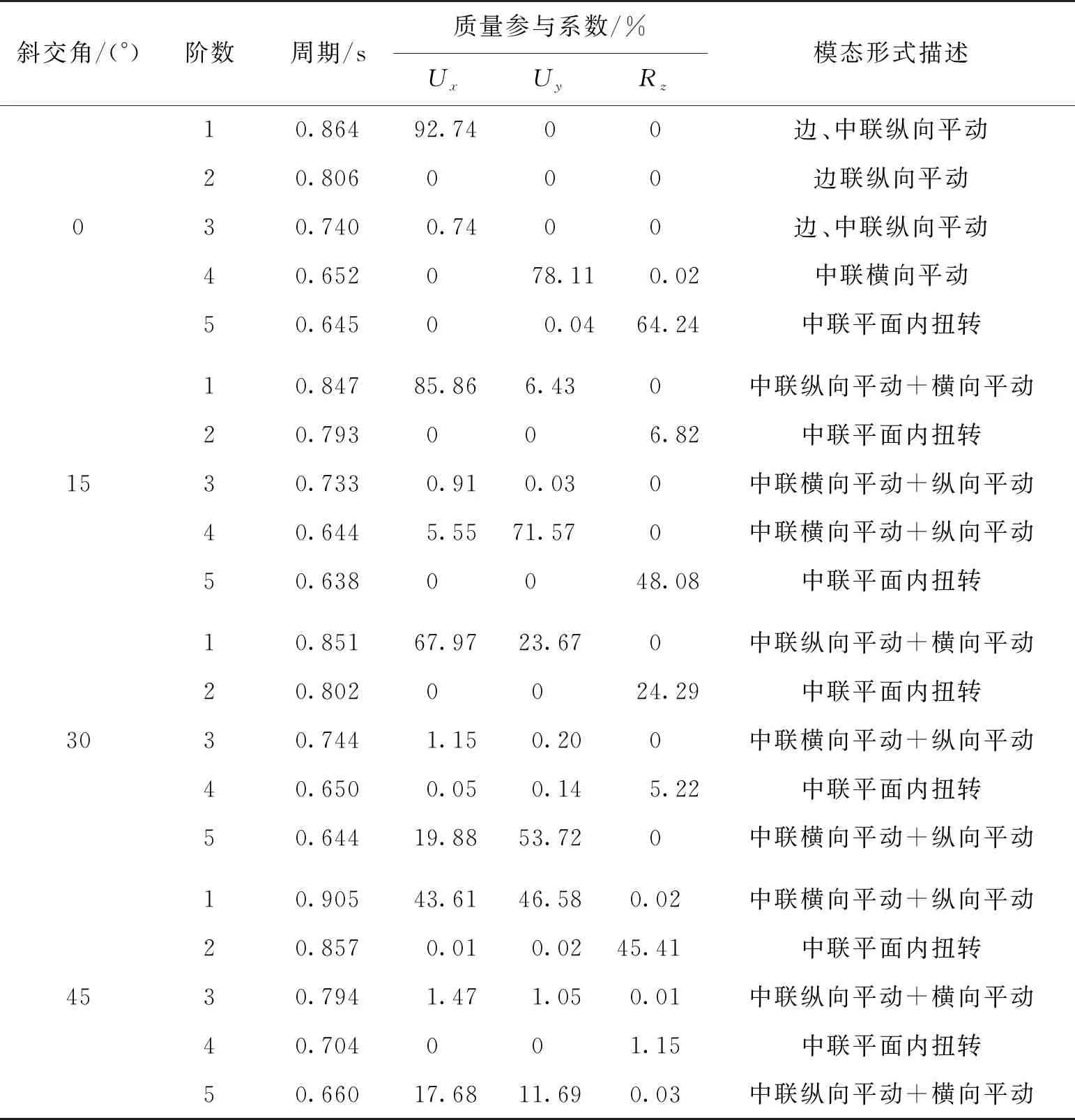
表1 斜交角0°、15°、30°和45°桥梁周期和质量参与系数
3 支座反力响应特性分析
以斜交角为45°的情况为例,对支座反力响应特性进行分析,表2列出了中间1联3跨在恒载和E2地震作用下的支座反力最大值和最小值,图6绘出了各支座反力的变化曲线。
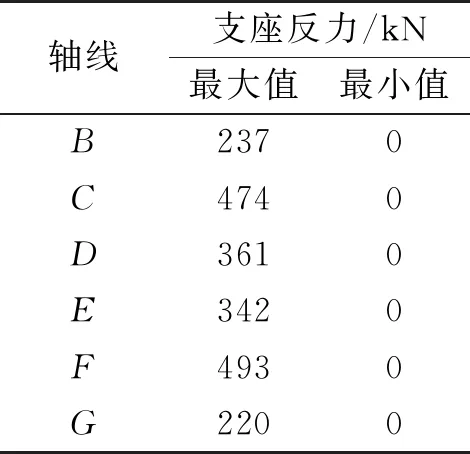
表2 在恒载和E2地震作用下的支座反力最大值和最小值
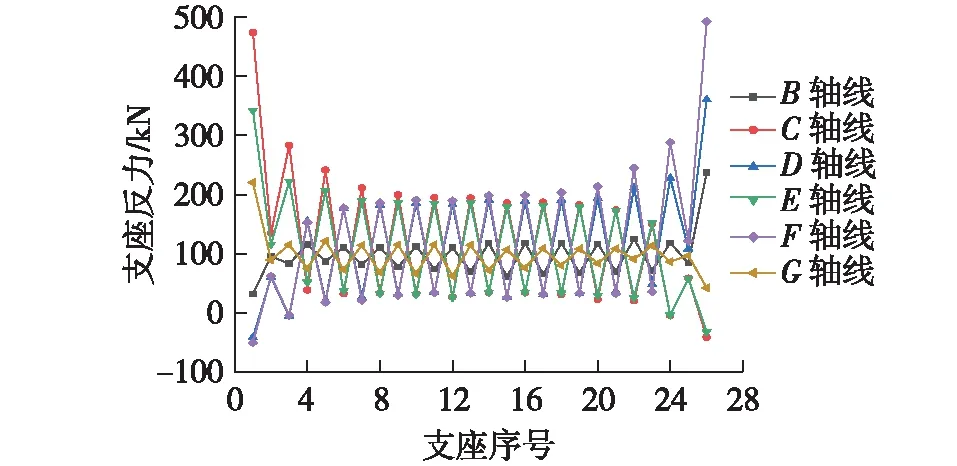
图6 在恒载和E2地震作用下的支座反力Fig.6 Bearing reaction forces under dead load and E2 earthquake
由表2可看出:斜交桥的支座响应受扭转效应影响较大,支座反力分布不均匀,最大支座反力出现在靠近边跨的C和F轴线,分别为474和493 kN,而支座反力容许值为452 kN,出现超压现象,支座会被压坏,需更换为竖向承载力更大的支座,同时每个轴线均有部分支座发生脱空。
由图6可见:从整个横截面来看,锐角侧支座反力最小,钝角侧支座反力最大,并呈现逐渐增大的趋势;以F轴线为例,从锐角侧到钝角侧,支座反力范围为-51~493 kN,靠近锐角侧的支座出现受拉现象,对于非受拉型的板式支座则表现为脱空。各轴线支座反力呈明显的锯齿状分布,中墩较边跨更为显著,即每块板的钝角侧支座反力均明显大于锐角侧,在E2地震作用下二者反力差值范围为91~371 kN,表现出显著的支座不均匀受力状态,呈现显著的竖向空间受力效应,该种受力状态会使空心板及铰缝区域产生较大的剪力,在新旧混凝土黏结部位发生剪切破坏。从顺桥向看,各轴线支座反力基本关于中间跨跨中对称分布,其中C、F轴线支座反力最大,其次为D、E轴线,边跨B、G轴线最小;边跨伸缩缝部位B、G轴线的支座反力受空间扭转效应影响较弱,分布相对较均匀且支座反力较小。
为了进一步分析地震作用下支座反力的分布特征,去除恒载作用,分别考虑水平向和竖向地震作用,结果如图7所示。此外,亦绘出自重作用下的支座反力分布,结果如图8所示。
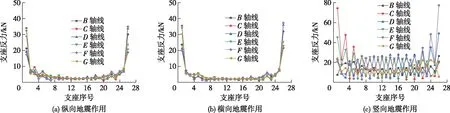
图7 在E2单向地震作用下的支座反力分布Fig.7 Distribution of bearing reaction forces under E2 unidirectional earthquake
由图7和8可看出:对于斜交桥,仅在自重作用下,支座反力即已表现出钝角侧大、锐角侧小的分布特征,在设计和运营养护过程中应重点关注钝角侧支座超压和锐角侧支座脱空问题;在竖向地震作用时,支座反力分布特征与自重作用相同;在纵、横向地震作用下,两侧支座反力相对较大,特别是钝角侧;几种效应相叠加,会加剧支座受力分布的不均匀性,导致斜交桥呈现较不利的空间受力特性。
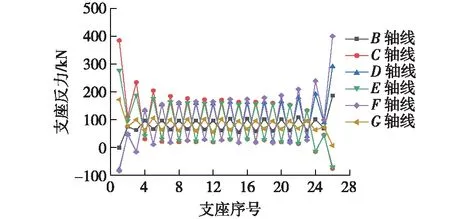
图8 自重作用下支座反力的分布Fig.8 Distribution of bearing reaction force under self-weight
上述地震响应特性会导致两个方面的危害:①中墩区域锐角侧支座出现脱空,空心板的整个受力体系发生变化,板内弯矩和剪力分布与正常受力状态有较大差异,可能导致因承载力不足而发生破坏;②中墩区域相邻板间的铰缝两侧支座反力有较大差异,将使铰缝承担较大剪力,可能导致铰缝特别是新旧混凝土黏结区域发生剪切破坏,为后期的维修加固带来较大的不便。
4 支座竖向受力影响因素
限于篇幅和考虑支座反力沿顺桥向的对称性,下文主要针对在E2地震作用下边跨B轴线、中墩C和D轴线支座反力进行分析。主要分析斜交角、盖梁刚度、跨径、桥宽对支座反力的影响,并且从支座刚度调整的角度研究改善支座反力分布不均匀的控制措施。
4.1 斜交角对支座反力分布的影响
为了研究斜交角对地震作用下支座反力分布的影响,根据斜交桥的实际情况分别选取斜交角为0°、15°、30°和45° 4种工况进行对比,支座刚度取371 kN/mm,结果如图9和表3所示。
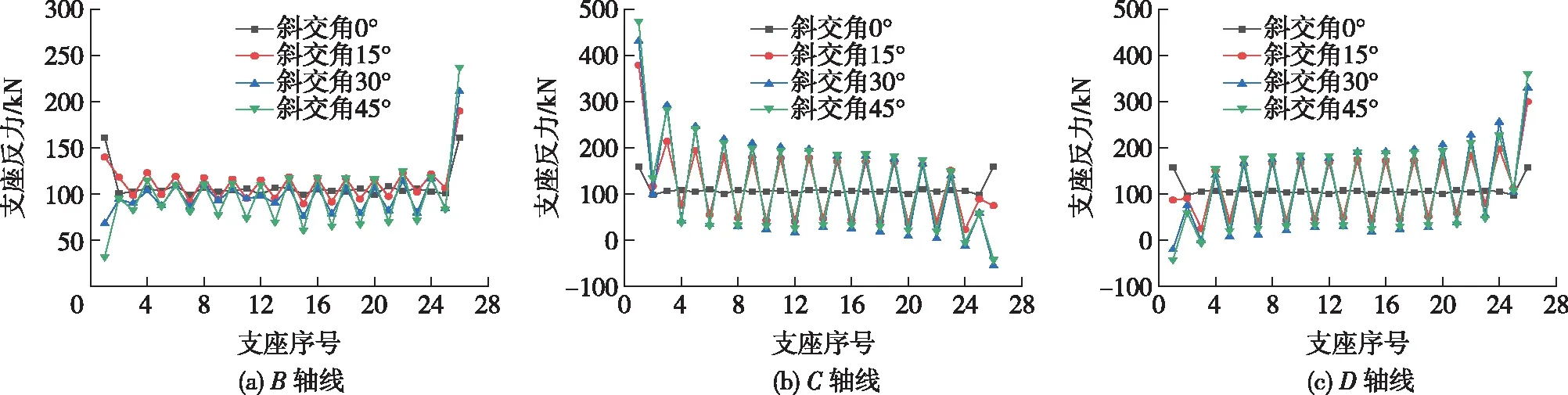
图9 不同斜交角下的支座反力Fig.9 Bearing reaction forces of different skew angles
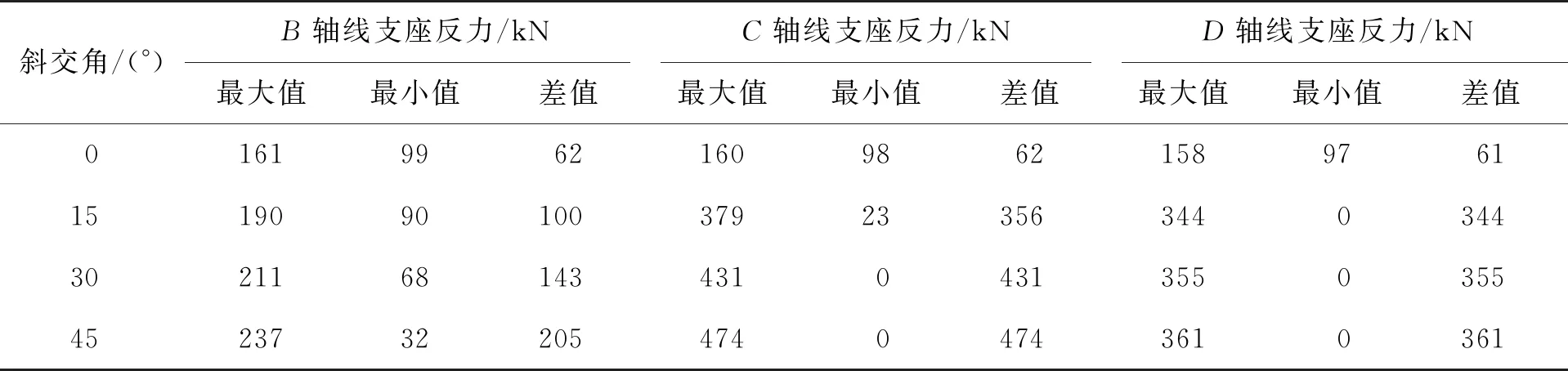
表3 不同斜交角下的支座反力最大值、最小值与差值
由图9和表3可以看出:当斜交角为0°(正交桥)时,各轴线支座反力分布非常均匀,除两端受到二期恒载影响支座反力较大外,其余支座反力均在100 kN左右。斜交桥的空间受力特性明显大于正交桥,支座反力的不均匀性更明显,如斜交角为15°时,B、C、D轴线的支座反力差值分别由62、62、61 kN增大至100、356、344 kN。伸缩缝处的支座(B轴线)受地震扭转效应影响较小,支座反力变化幅度相对较小;其他轴线处支座反力受斜交角影响较大,随着斜交角的增大,支座反力的不均匀性增强,但增强程度有所减弱。当斜交角为15°时,最大支座反力比正交桥时显著增大,最小支座反力也明显减小,支座反力差值大幅度增加;当斜交角增大至30°和45°时,支座反力的变化幅度有所减小。当斜交角大于15°时,在地震作用下锐角侧支座可能发生脱空;当斜交角大于30°时,钝角侧支座可能发生超压破坏。由此可知,在地震作用下,斜交桥支座竖向受力较为不利,特别是斜交角较大的情况。在设计时,应尽量避免大斜交角的情况,若无法避免,则需采取有效措施。
4.2 盖梁刚度对支座反力分布的影响
由于支座反力与支座的压缩变形相关性较大,盖梁的变形可能会对支座变形造成影响,因此,需对盖梁的刚度进行研究。通过调整盖梁高度和跨度两种方式改变盖梁刚度,其中跨度的调整通过改变桥墩数量来实现。以斜交角为45°的情况为例,支座刚度依然取371 kN/mm,盖梁高度取0.8、1.2、1.6 m 3种工况,分别采用设置3个桥墩(图1)和去除中间桥墩(图10)2种工况进行对比,跨径及其他条件都保持相同。限于篇幅,只绘出中墩C、D轴线线支座的变化曲线,如图11和12所示。

图10 去除中间桥墩的桥梁横剖面示意图(m)Fig.10 Schematic diagram of cross section of bridge removing middle pier (m)
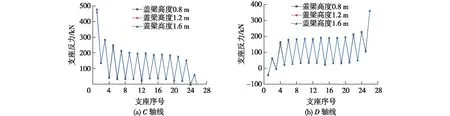
图11 不同盖梁高度下的支座反力Fig.11 Bearing reaction forces of different capping beam heights
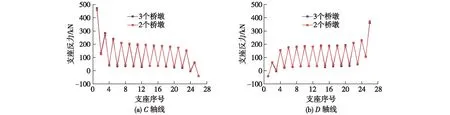
图12 不同墩间距下的支座反力Fig.12 Bearing reaction forces of different pier spacings
由图11和12可知:盖梁高度和跨度的改变对支座反力的分布影响很小,即可忽略盖梁的刚度对支座反力分布的影响。在设计时,只需根据结构受力要求和经济性确定盖梁尺寸和墩柱的布置即可。
4.3 跨径对支座反力分布的影响
跨径的改变影响斜交桥上部结构的质量和刚度,导致上、下部结构刚度比发生变化,这种变化可能对斜交桥的空间受力性能产生影响,因此,需对跨径对支座反力分布的影响进行分析。跨径分别取13、16和20 m,桥面宽度为13 m,在E2地震作用下的支座反力分布如图13和表4所示。
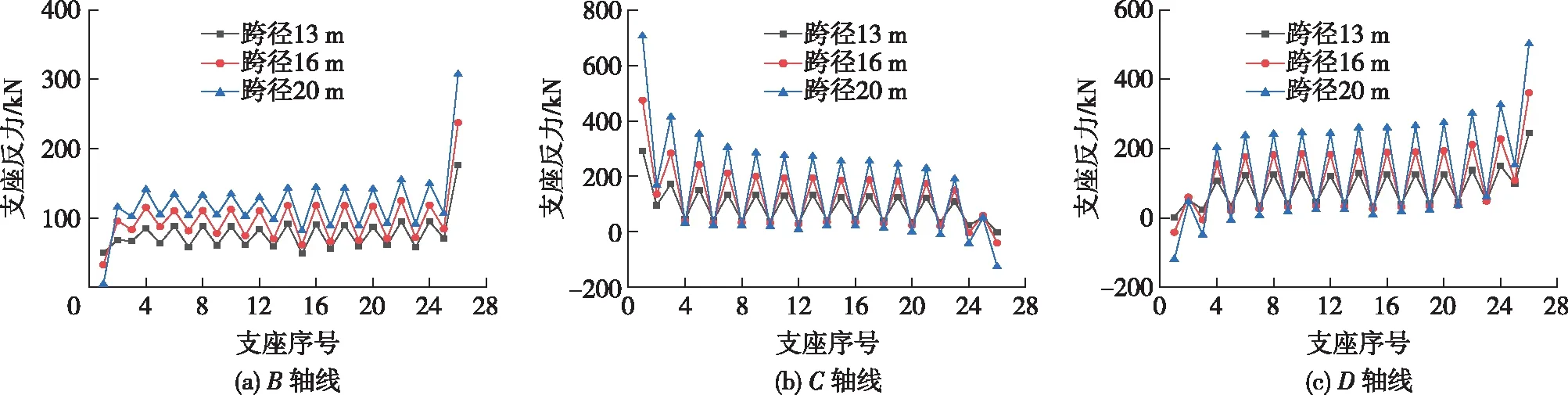
图13 不同跨径下的支座反力Fig.13 Bearing reaction forces of different spans

表4 不同跨径下的支座反力最大值、最小值与差值
由图13和表4可以看出:随着跨径的增大,整个横截面的钝角侧支座反力有较大幅度的增大,锐角侧有所减小,但减小幅度相对较小,支座反力差随跨径的增大逐渐增大,支座反力的不均匀性逐渐增强,空间受力特征逐渐显著。随着跨径的增大,每块板钝角侧和锐角侧支座反力的变化规律与整个截面的规律相近,钝角侧支座反力的增大幅度大于锐角侧,支座反力差值逐渐增大,尤其中墩C、D轴线变化更为显著,如B轴线每块板13、16和20 m跨径的平均支座反力差值分别为38、57和67 kN,C轴线分别为108、195和307 kN,D轴线分别为97、177和268 kN,即随着跨径的增大,每块板钝角侧和锐角侧支座的不均匀性逐渐增强,加剧了锐角侧支座脱空的风险,对跨度较大的空心板桥,尤其需要关注支座脱空以及空心板横向空间受力性能。
4.4 桥宽对支座反力分布的影响
为了分析桥宽对支座反力分布的影响,跨径取13 m,桥宽分别取13、17和21 m,斜交角为45°,在E2地震作用下的计算结果如图14和表5所示。

图14 不同桥宽下的支座反力Fig.14 Bearing reaction force of different bridge widths
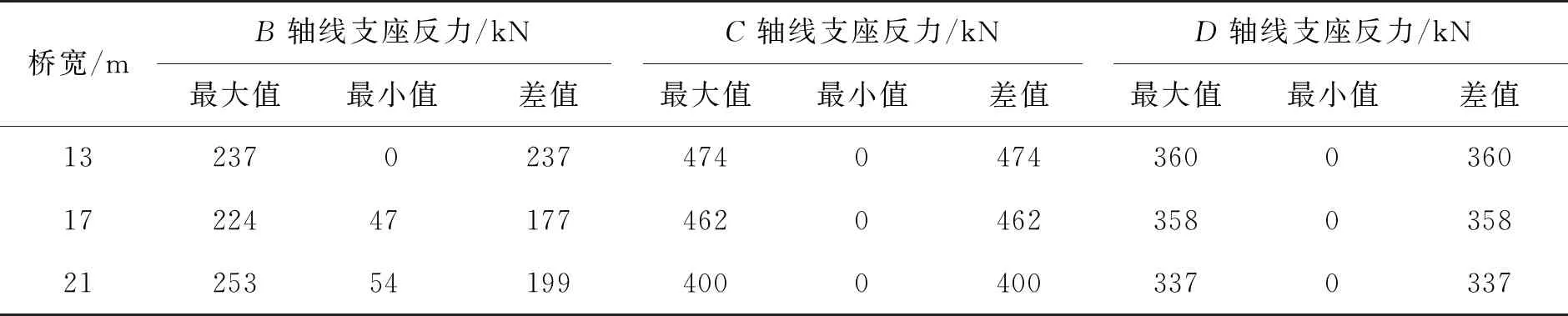
表5 不同桥宽下的支座反力最大值、最小值与差值
由图14和表5可知:B轴线支座反力差值较小,随着桥宽的增大,差值没有明显的变化;C和D轴线受扭转效应影响较大,支座反力差值明显更大,且随着桥宽的增大,差值呈减小的趋势,说明随着桥宽的增大,地震作用时的空间扭转效应影响减弱。
4.5 支座刚度对支座反力分布的影响
以斜交角45°的斜交桥为例,通过改变支座竖向刚度来探讨支座刚度对地震作用下支座反力分布的影响,选用直径250 mm的橡胶支座,厚度为29、37、45和53 mm(对应支座竖向刚度分别为474、371、305和259 kN/mm),竖向承载力Rck=452 kN,计算的桥梁支座反力如图15所示。不同刚度下B、C、D轴线的支座反力最大值、最小值以及差值见表6。
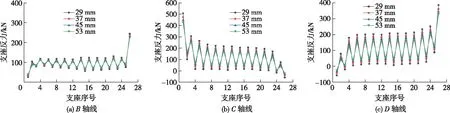
图15 不同刚度下的支座反力Fig.15 Bearing reaction forces of different stiffness

表6 不同刚度下的支座反力最大值、最小值与差值
由图15和表6可知:随着支座竖向刚度的逐渐减小,各轴线支座反力最大值逐渐减小,最小值逐渐增大,同一轴线支座反力差值逐渐降低,支座反力的分布逐渐趋于均匀;橡胶厚度从29 mm增加到53 mm时,即支座竖向刚度由474 kN/mm减小到259 kN/mm时,各轴线支座反力差值均降低15%左右,支座受力更均匀,当支座刚度减小到305 kN/mm时,在地震作用下,各支座反力均小于竖向承载力,不会发生超压破坏,但锐角侧最边上的支座依然可能发生脱空,需设置抗拉支座或采取其他措施。
根据各板的受力特点,对各板钝角处和锐角处的支座刚度进行调整,钝角处设置刚度较小的支座,刚度取259 kN/mm(橡胶厚度53 mm),锐角处设置刚度较大的支座,刚度取为474 kN/mm(橡胶厚度29 mm),支座设置方案调整前后支座反力变化如图16所示。
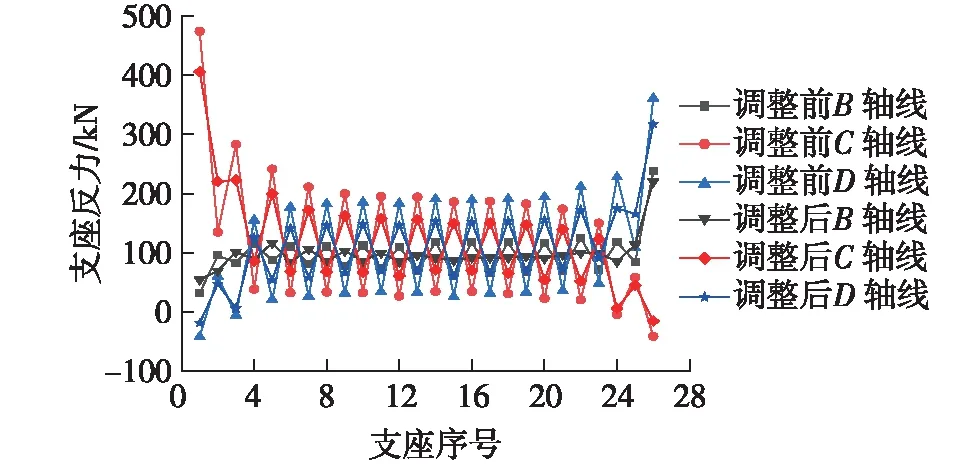
图16 支座设置方案调整前后支座反力对比曲线Fig.16 Comparison curves of bearing reaction force before and after adjustment of bearing layout scheme
由图16可知:支座设置方案调整后,各板块钝角侧反力减小,锐角侧反力增大,支座反力差值明显降低。如B、C和D轴线平均支座反力差值分别由原来的52、180和164 kN降为0.7、104和93 kN,降幅达98.7%、42.2%和43.3%,对支座受力不均匀性的改善效果显著,可有效降低空心板内部以及铰缝区域的受力。从整个横截面来看,钝角侧的支座反力亦有一定程度的降低,锐角侧支座反力有所增大,可改善支座超压和脱空的问题。
5 结论与建议
1)先简支后桥面连续空心板斜交桥前5阶主导振型均表现出全桥的面内平动、面内扭转或者面内平动与平动、平动与扭转的耦合,且随着斜交角的增大,结构在空间上的耦联现象越明显,抗扭刚度相对减弱,扭转效应增大,桥面扭转振型前移。因此,对倾斜角度相对较大的斜交桥,地震计算时应考虑整体结构的空间耦联性。
2)斜交桥仅在自重作用下,支座反力即已表现出钝角侧大、锐角侧小的分布特征,每块空心板也表现出相同的变化规律;地震作用加剧了支座受力分布的不均匀,导致斜交桥呈现较不利的空间受力特性,使得铰缝承担较大剪力,特别是新旧混凝土黏结区域可能发生剪切破坏,为后期的维修加固带来较大的不便。因此,在设计和运营养护过程中应关注斜交桥的该受力特性,尤其需关注钝角侧支座超压和锐角侧支座脱空问题。
3)斜交桥的空间受力特性明显大于正交桥,支座反力的不均匀性更明显,钝角侧的支座反力可数倍于同跨径的正交桥;伸缩缝处的支座反力受地震扭转效应影响相对较小,其他轴线支座反力差值较大,并且受斜交角影响较大,随着斜交角的增大,支座反力的不均匀性增强。因此,在设计时应尽量避免大斜交角的情况,若无法避免,则需采取有效措施。
4)随着桥宽的增大,中墩支座反力差值呈现减小的趋势,地震作用时的空间扭转效应影响减弱;随着跨径的增大,整个横截面及每块空心板均表现出钝角侧支座反力有较大幅度的增大、锐角侧的有所减小、支座反力差值逐渐增大、空间受力特征逐渐凸显的特性,会加剧锐角侧支座脱空的风险。因此,对跨度较大的空心板桥,需关注支座脱空以及空心板横向空间受力性能。盖梁高度和跨度的改变对支座反力的分布影响很小,可忽略盖梁刚度对支座反力的影响。
5)各轴线支座反力的不均匀性随支座竖向刚度的减小而减小,降低支座的竖向刚度可有效改善支座受力不均,降低支座脱空和超压发生的概率;对于斜交桥,在各板块的钝角侧设置刚度较小的支座,在锐角侧设置刚度较大的支座可显著改善支座的受力不均。降低各轴线支座反力差值,不仅可控制支座脱空和超压,而且可有效降低板内剪力和铰缝区域剪力,改善空心板桥的横向空间受力性能。

