基于交叉验证梯度提升决策树的管道腐蚀速率预测

颜 佳,黄 一,王晓娜

(1. 大连理工大学 船舶工程学院，大连 116024； 2. 大连理工大学 物理学院，大连 116024)

输油管道腐蚀速率的准确预测能够为管道运营商及时采取有效的维护措施提供依据，对于保障管道安全高效运行具有重要的意义。但是管道的腐蚀速率和腐蚀环境因素之间存在复杂的非线性关系，很难用传统的数理方法建立其数学模型。近几年来，更多的学者开始将基于数据驱动的机器学习方法引入到腐蚀预测领域，取得了不错的预测效果。他们采用的方法主要有BP神经网络(BPNN)[1-3]和支持向量机 (SVM)[4-6]等。但是这些方法也有一些缺点：一方面，BPNN与SVM方法需要对输入信息进行预处理(如正则化，特征映射等)[7]，增加了建模的工作量；另一方面，这些方法建立的都是单一全局模型，只能从某一方面对历史腐蚀数据进行学习，学习不够充分，因此其预测结果具有不稳定性，特别是神经网络模型受权重初值的影响较大，得到的结果有时甚至很不理想。

与单一模型不同，集成学习模型能够重复利用已有数据信息训练多个基学习器，并通过一定的结合策略形成一个强学习器进行预测。已有的研究表明，与单一模型相比，集成模型的预测结果往往具有更高的精确性与鲁棒性[8]。而梯度提升决策树(GBDT)作为一种常见而高效的集成学习方法，近年来在价格预测[9]，城市智能交通管理[10-12]和电力系统负荷预测[13-14]等领域得到了广泛的应用。本工作基于梯度提升决策树算法建立管道腐蚀速率预测模型，利用k折交叉验证和网格搜索技术进行参数寻优，实例验证结果表明其具有预测精度高和泛化能力强的优点，可为将来的管道腐蚀速率预测提供一种新方法。

1 梯度提升决策树模型

1.1 提升算法

集成学习方法通过结合某种学习算法构建多个基学习器,提高单个学习器的泛化能力与鲁棒性[15]。提升算法是集成学习方法中非常重要的一类，它通常涉及两个部分——前向分步算法和加法模型[16]。

前向分步算法是指在训练过程中，下一轮迭代产生的基学习器是在上一轮的基础上训练得来的，每增加一个基学习器即是对上一个模型的修正，因此该模型可以用式(1)表示。

Fm(x)=Fm-1(x)+γmhm(x)

(1)

式中：Fm为第m次迭代后得到的集成模型；hm(x)为第m个基学习器；γm为第m个基学习器在集成模型中的权重。

加法模型是指迭代完成后得到的强学习器可表示为多个基学习器线性相加的形式，如式(2)所示。

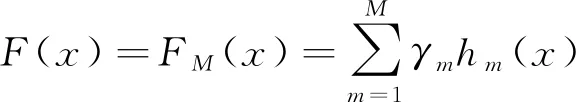
(2)

式中：FM(x)为最终的集成模型；M为基学习器的个数。

1.2 梯度提升决策树(GBDT)

GBDT是FRIEDMAN[17]基于提升算法框架提出的一种新的机器学习方法，同时也是对传统提升算法的一种改进。其基本思想是把损失函数的负梯度在当前模型下的值作为模型预测结果的近似残差，并把该值作为下一个模型的训练目标，通过迭代过程逐步减小预测偏差[10,18]，提高预测精度。GBDT使用决策树模型作为基学习器。决策树模型是基于单特征比较构建的，不对数据进行预处理也可以很好地拟合数据。GBDT将提升算法和决策树模型两者的优点结合起来，因此被认为是机器学习中功能最强大的算法之一。

假设已知的数据集为：

T={(x(i),y(i))|i=1,2,…N}⊆Rn×R

(3)

(4)

但是，在每一步迭代过程中，对于任意损失函数L[y,F(x)]，依据式(4)求出最优的函数解h(x)在计算上是十分困难的。因此，一般采用启发式算法，通过不断地迭代来逐步逼近精确解。根据这个思想，GBDT使用最速下降法来求解该最小化问题。假设选取的损失函数在当前集成模型Fm-1上可微，则最速下降方向是损失函数在Fm-1处的负梯度方向，即令：

(5)

则更新模型为：

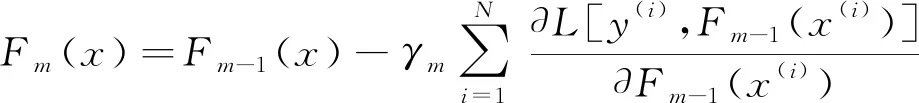
(6)

其中，步长γm可以通过一维线搜索求得，即：

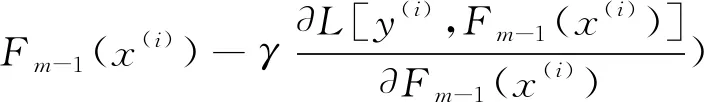
(7)

为了防止过拟合，FRIEDMAN等[17]提出了一种简单的正则化方法，通过学习率v来控制每个基学习器对集成模型的贡献程度，最终的模型则可以表示为：

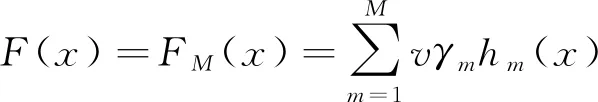
(8)

1.3 参数选择与交叉验证

由式(8)可以看出，GBDT的预测精度和泛化能力主要取决于集成模型中决策树的数量M，学习率v以及每个决策树模型hm(x)的复杂度(以最大叶子节点数J表示)。一般而言，较小的学习率意味着需要更多的决策树模型才能达到要求的预测精度，而生成过多的决策树会消耗大量的计算资源[20]。研究表明，将学习率v设置为一个较小的值(v≤0.1)，能够避免因过快逼近造成的过拟合问题，从而减小测试误差[21]。单棵决策树的叶子节点数越多，本身学习能力就越强，集成模型中需要的决策树就越少，但这不利于发挥集成算法的优势。HASTIE等[21]认为在GBDT中，当4≤J≤8时，模型效果表现最佳。

本工作通过k折交叉验证来寻找模型的最优超参数组合，降低模型潜在的过拟合风险。运行k折交叉验证时，首先将样本集随机划分为k份，每份的样本数量大体相等。然后依次选取第i份数据作为测试集，其余k-1份数据作为训练集对模型进行训练，最终得到k个模型，把k个模型在各自测试集上预测效果的平均值作为判断该超参数取值下模型性能的依据[22]。

k折交叉验证使用无重复抽样技术，使得每一个样本都有一次机会作为测试样本，提高了数据的利用率，是模型性能评估的有效方法[23]。k折交叉验证选择最优超参数建立梯度提升决策树模型的流程图如图1所示，其中超参数集Pi={Mi,vi,Ji}。

图1 k折交叉验证选择最优超参数建立梯度提升决策树模型的流程图Fig. 1 Flow chart of selecting optimal hyper-parameters to establish gradient boosting decision tree model through k-fold cross validation

2 GBDT在管道腐蚀速率预测中的应用

2.1 数据来源

某输油管道材料为20号钢，使用压力为1.0～5.0 MPa，输送介质为产地不同的原油。影响该管道内腐蚀速率的主要环境因素为硫含量，酸值，温度，流速和压力，通过正交试验方法实测得到的腐蚀速率如表1所示[5]。将环境因素作为模型输入，腐蚀速率实测值作为期望输出，建立梯度提升决策树预测模型。

2.2 建立模型

为了测试模型的泛化能力，首先将所有的样本按照4∶1的比例随机划分为训练集和测试集。在建模时，选取决策树数量M的集合为{50,100,150,200,250}，学习率v的集合为{0.001,0.005,0.01,0.025,0.05,0.075}以及每棵决策树最大叶子节点数J的集合为{4,5,6,7,8}，利用网格搜索技术遍历所有可能的参数组合，根据最小均方误差准则，对于训练集中的数据采用5折交叉验证方法确定模型的最优参数。在交叉验证时，由于模型从未使用过测试集中的样本，因此模型在测试集上的预测性能能够反映其真实的泛化能力。为了进行对比分析，使用BP神经网络(BPNN)和支持向量机(SVM)方法在同一数据集上进行建模。

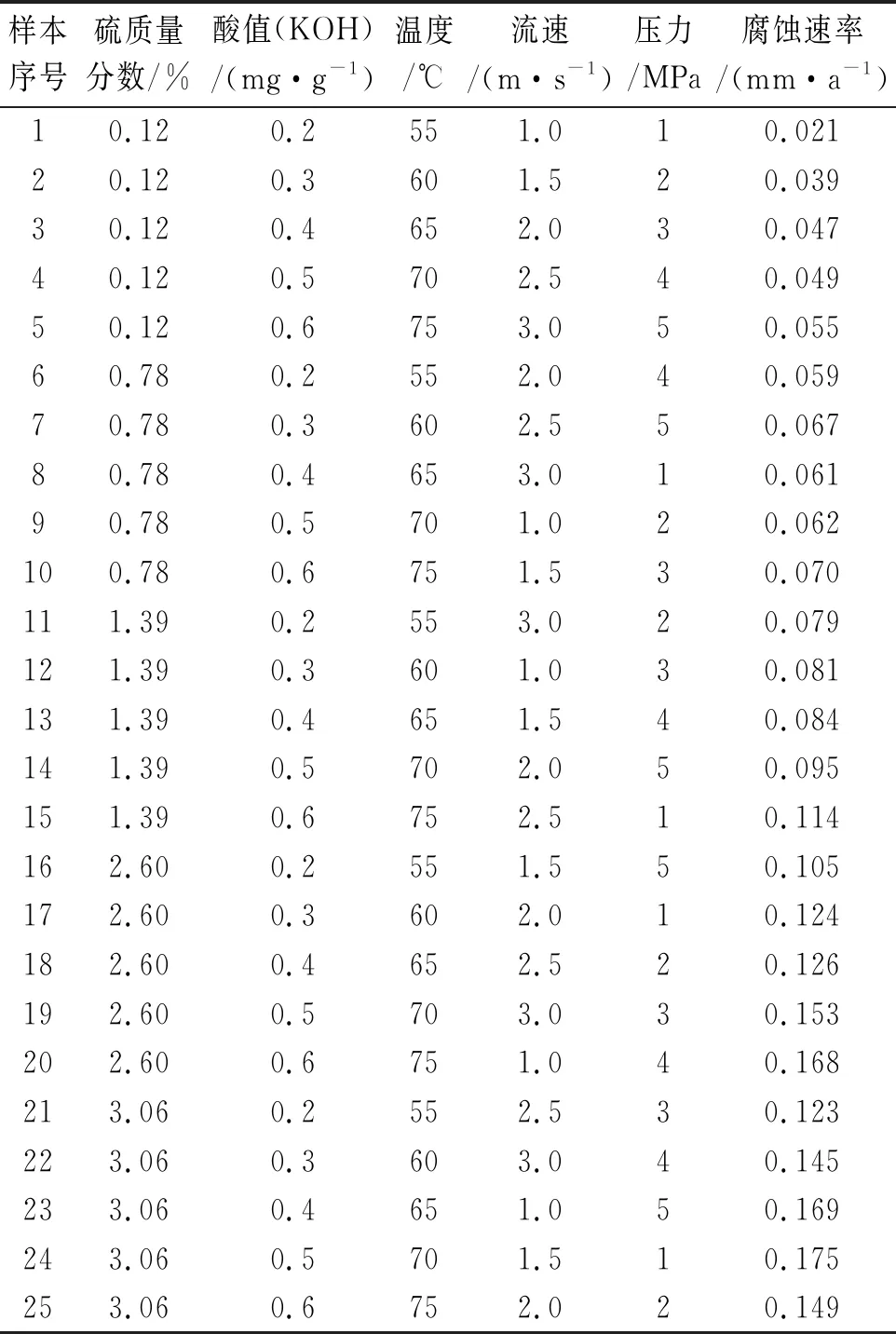
表1 某输油管道实测腐蚀速率Tab. 1 Measured corrosion rates of an oil pipeline

2.3 预测精度评估指标

为了评估模型的整体性能，选择均方误差EMSE，平均绝对百分误差EMAPE和决定系数R2等3个指标来衡量模型的预测精度，计算公式分别如式(9)～(11)所示。其中，均方误差能很好地反映预测误差的实际情况，平均绝对百分误差是衡量模型相对误差最重要的指标，决定系数是回归预测拟合优度的度量。

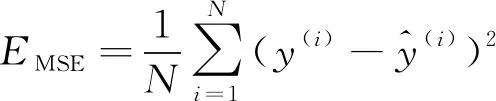
(9)

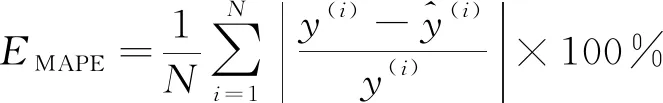
(10)

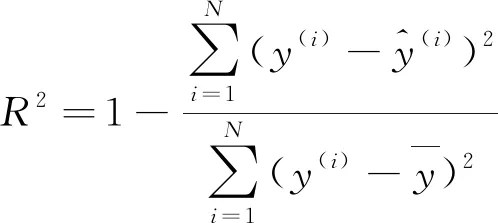
(11)

3 结果与分析

3.1 模型预测结果比较

在建模中，通过随机划分将序号为25，2，24，4和20的样本划入测试集，其余样本作为训练集。通过网格搜索和交叉验证得到GBDT模型的最优参数M=100,v=0.075,J=4。GBDT、BPNN和SVM三种模型在训练集与测试集上的预测值和相对误差如表2所示，预测值的残差如图2所示。

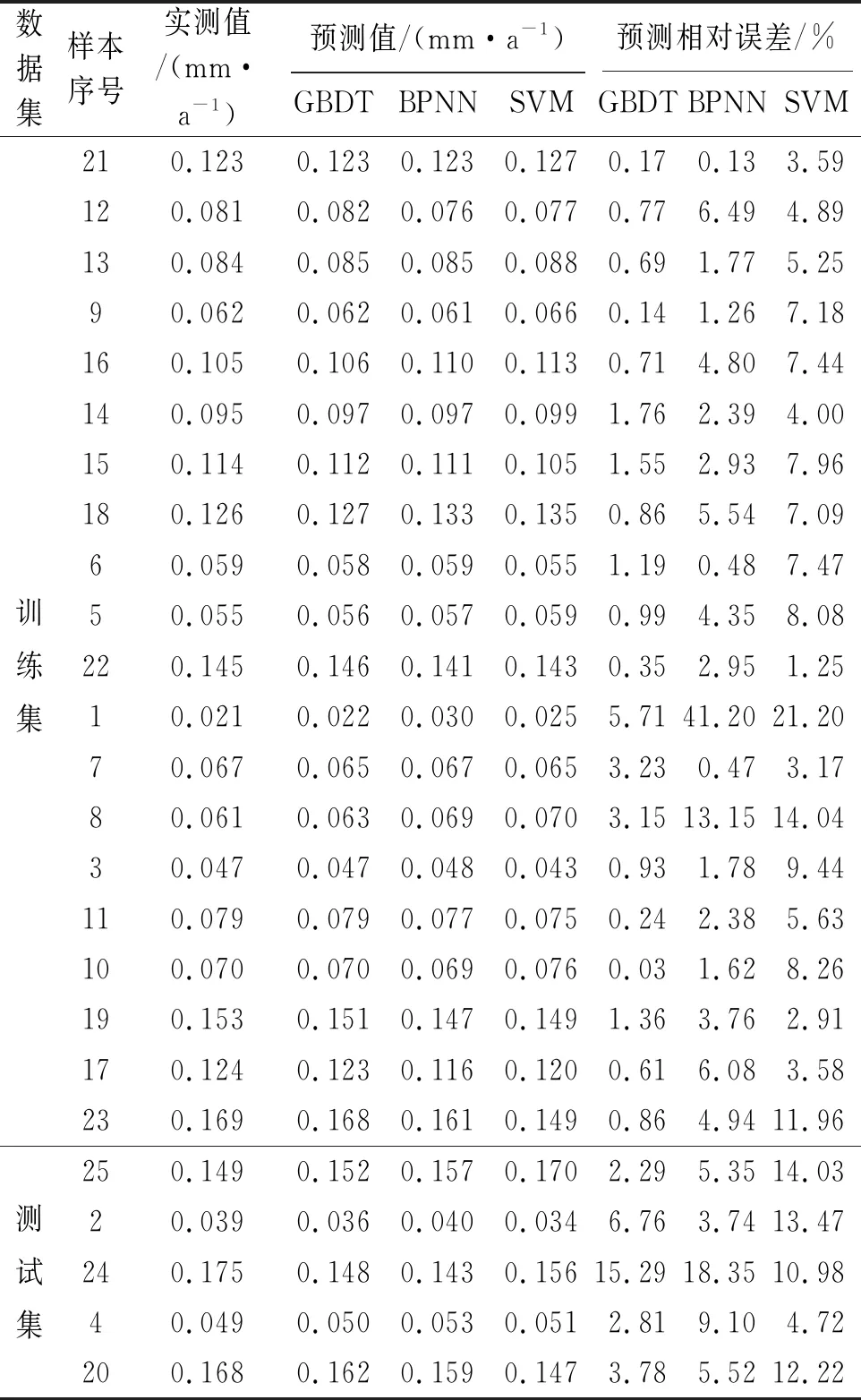
表2 三种模型腐蚀速率的预测值和相对误差Tab. 2 Predicted corrosion rates and relative errors of three models

从表2和图2中可以直观地看出，SVM模型的预测效果较差:一方面其预测值的相对误差和残差大都高于BPNN模型与GBDT模型的相对误差和残差;另一方面该模型在测试集上的预测残差远大于在训练集上的预测残差，出现了“过拟合”现象。这说明SVM模型的泛化能力比GBDT模型要差一些。对于腐蚀速率最小的第1个样本，三种模型预测值的相对误差都很大，说明模型对于数据集中最值的预测能力都有待提高。但三种模型预测值的绝对误差仍在可接受的范围内，且相比于BPNN模型与SVM模型，GBDT模型的预测精度有了很大的提高，预测相对误差仅为5.71%。

图2 三种模型预测值的残差Fig. 2 Residual errors of predicted values by three models

为了量化模型的整体预测性能，利用式(9)～(11)计算得到模型预测精度指标如表3所示。

表3 GBDT、BPNN与SVM模型预测精度指标Tab. 3 Prediction accuracy indexes of GBDT,BPNN and SVM models

从表3中可以看出，BPNN和SVM模型预测结果的平均绝对百分误差分别为6.03%和7.99%，而GBDT模型只有2.25%，且该模型的均方误差值小；GBDT模型的决定系数比BPNN和SVM模型的决定系数更接近于1，说明GBDT模型的整体预测效果最好。

为了消除单个数据可能带来的随机性误差，对预测值与实测值进行线性拟合分析，结果如图3所示。

从图3中可以看出，三个模型的预测结果都落在理想拟合直线附近。但是相比较而言，BPNN和SVM模型的预测结果的实际拟合直线离理想拟合直线更远一些。此外，对于最大腐蚀速率样本点，三种模型的预测结果都明显地偏离了理想拟合直线，而该样本点恰好在测试集中，说明三种模型的外推能力都比较弱。

以上各方面的对比分析表明，对于管道腐蚀速率预测，本工作提出的GBDT模型能够更好地拟合实测数据，其综合性能要优于BPNN与SVN模型。

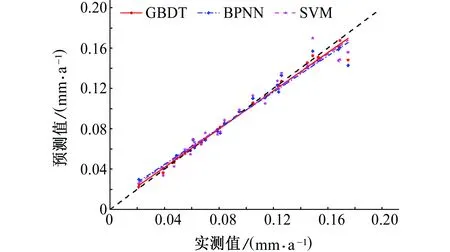
图3 预测值与实测值之间的线性拟合Fig. 3 Linear fitting between predicted values and measured values

3.2 对GBDT模型的进一步分析

由式(8)可以看出，GBDT模型的预测精度受到模型中决策树数量M的影响。图4显示了当学习率v=0.075，最大叶子节点数J=4时，包含不同决策树数量的GBDT模型预测值与实测值的对比结果。从图4中可以看出，随着M的增加，模型预测值与实测值之间的偏差越来越小，说明增加决策树能够提高模型的预测性能。但是当决策树达到一定数量后，再增加其数量对模型预测能力的提升作用不大。为了进一步验证这一观点，绘制模型预测值的平均相对误差与决策树数量的关系图，如图5所示。

从图5中可以看出，当决策树数量小于70时，GBDT模型在训练集和测试集上的平均相对误差随决策树数量的增加都迅速减小，这与BÜHLMANN等[24]的分析结果一致，即随着决策树数量的增长，集成模型的预测偏差呈指数型衰减。当决策树数量大于70时，GBDT模型在训练集上的平均相对误差继续减小，但减小速率变慢，而在测试集上的平均相对误差略微上升，说明此时模型开始出现“过拟合”现象。在这种情况下，可使模型训练提前停止，在不降低模型的整体性能的情况下缩短训练时间。

(a) M=1 (b) M=2 (c) M=5

(d) M=10 (e) M=20 (f) M=50

(g) M=100 (f) M=150 (i) M=200图4 包含不同决策树数量的GBDT模型的预测结果Fig. 4 Prediction results of GBDT model with different number of decision trees

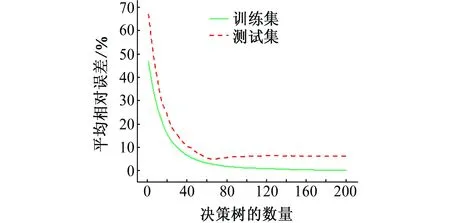
图5 GBDT模型平均相对误差与决策树的数量之间的关系Fig. 5 Relationship between average relative error and number of decision trees for GBDT model

4 结论

(1) 实例验证结果表明，对于管道腐蚀速率预测，梯度提升决策树模型能够取得很高的预测精度，其预测结果可为了解管道运行状况及采取适时的维护措施提供参考依据。

(2) 与广泛应用的BPNN和SVM预测模型对比可以发现，基于集成思想的梯度提升决策树模型不仅能很好地拟合已知数据，而且对未知数据具有很强的泛化能力，因此具有更大的实用价值。

(3)在梯度提升决策树模型构建过程中，随着决策树数量的增加，模型预测偏差的减小程度会迅速降低，因此选择恰当的决策树数量，对于缩短模型的训练时间和防止“过拟合”现象至关重要。