基于传递函数模型的飞机腐蚀结构可靠性评估

张春晓,侯立国,易 威

(1. 中国民航大学 天津市民用航空器适航与维修重点实验室，天津 300300；2. 中国民航大学 理学院，天津 300300;3. 北京飞机维修工程有限公司，北京 100080)

长期在高温、高湿和盐雾等环境中服役会导致飞机结构件表面的防护涂层系统不断老化和剥落，基体材料严重腐蚀，从而使飞机的飞行性能下降，安全使用寿命缩短。同时，由于在服役过程中受到环境与载荷的联合作用，许多飞机结构因腐蚀损伤而提前失效，甚至突然断裂。因此，飞机结构的腐蚀损伤不仅会导致飞机在飞行中出现故障，严重时还会诱发重大安全事故。例如，2002年美国两架F15飞机因重要部件腐蚀损伤导致空中解体，这两起事故使全球768架飞机停飞检查，并有180多架飞机因此退役[1]。2008年10月和12月在俄罗斯赤塔地区接连发生两起米格-29飞机坠毁事故，俄罗斯空军对在役飞机进行全面检查时发现，30%以上的米格-29飞机存在严重腐蚀，腐蚀问题也是导致大部分该型飞机提前退役的直接原因[2]。我国X1系列飞机也先后发生了多起由严重腐蚀引起的故障。例如，2001年该系列飞机42框下半框发生腐蚀断裂，导致1架飞机报废；2002年该系列飞机机翼前梁和油箱下壁板等部位又发生严重腐蚀，导致两架飞机提前返场大修[1]。

随着全球机队规模的不断扩大，飞机的腐蚀也日益增加，针对该问题的研究也引起了国内外科研人员广泛关注。早在20世纪60年代，美国先后研究并制订了与飞机腐蚀相关的标准规范[2]。1994年，HARLOW等[3]对腐蚀条件下飞机结构腐蚀的全寿命过程进行了研究,并建立了飞机结构件使用寿命的预测模型。2007年，张有宏等[4]针对飞机停放位置及飞行环境的差异,给出了详细的环境模型,并对机体的腐蚀损伤进行测量与统计分析,得到腐蚀损伤随环境和服役时间演化规律的概率模型。

我国民航业起步较晚，对飞机腐蚀问题的研究从20世纪90年代才开始，飞机腐蚀方面的数据有限，因此对该问题的数理统计分析相对较少。张福泽[5]提出了一种计算金属机件腐蚀损伤的日历持续时间(寿命)计算模型，该模型适用于腐蚀环境中飞机日历寿命的确定。潘波等[6]基于故障树分析和模糊理论的方法，对飞机结构在复杂环境中发生的腐蚀损伤进行了综合评判。陈跃良等[7]提出了基于不连续状态腐蚀与疲劳交互作用下飞机结构的全寿命评估模型。

本工作在前人研究的基础上，建立传递函数模型预测飞机结构的腐蚀状况，同时建立腐蚀条件下飞机结构可靠度的概率模型，科学合理地预测腐蚀条件下飞机结构的剩余寿命，为有效评估飞机结构的持续适航性提供参考。

1 传递函数模型的构建

传递函数模型在时间序列模型的基础上考虑了对研究对象有影响的一些其他因素，因此该模型的应用较为广泛[8]。腐蚀条件下，飞机结构的使用寿命除受时间影响外，还受到腐蚀深度的影响。一般来说，腐蚀深度越深，寿命越短。因此，传递函数模型考虑了腐蚀深度的影响，揭示了腐蚀发展时间与腐蚀深度之间的内在联系。

1.1 传递函数模型形式

一般来说，将研究的时间序列记为Yt，它有N个观测值。假设{Yt}不仅受其过去观测值和随机扰动项{at}的影响，而且与另一个时间序列{Xt}有关，其传递函数模型形式如式(1)所示。

φ(B)Yt=φ(B)Xt+θ(B)at,t=1,2,…,N

(1)

更一般的模型可表示为

Yt=V(B)Xt+N(B)at

(2)

其中，

(3)

(4)

V(B)称为传递函数，表示将输入序列{Xt}传递到输出序列{Yt}，其与随机扰动项{at}叠加后，得到实际的输出序列{Yt}。

1.2 数据来源

一般来说，飞机结构件的腐蚀损伤会采用多个指标来衡量，如腐蚀深度、腐蚀面积和腐蚀体积等。考虑到飞机结构部件的腐蚀以点蚀为主，且无裂纹现象，被更换(寿命终止)的飞机结构件处于蚀孔生长时期，故采用腐蚀深度作为衡量腐蚀状况的指标。

本工作采用的腐蚀深度数据来自同一个机场、同一架飞机的隔框结构，材料、工艺及维修体系等各方面条件相同。不同腐蚀发展时间对应的腐蚀深度数据见表1。

1.3 模型建立

将测得的隔框腐蚀深度数据作为一个母体考虑。假设发生点蚀的飞机结构件的腐蚀深度为Dt，相应的蚀孔发展时间为Xt。由文献[9]可知蚀孔发展时间Xt与腐蚀深度Dt的三次方成正比，所以对Xt选取的传递函数形式为：

φ(B)Xt=kDt3+θ(B)at,t=1,2,…,30

(5)

基于表1所给数据，应用SPSS软件建立模型，见式(3)，采用最大似然法对模型参数进行估计，通过AIC准则选择最终模型为：

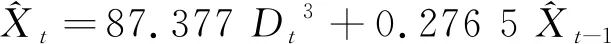
(6)

对该模型进行拟合优度检验和参数显著性t检验，结果如表2所示。由表2可知，该模型的拟合优度为0.999，近似为1，说明该传递函数模型的拟合效果很好。给定显著性水平为0.05，表2中模型参数k和φ的t检验显著性P值均小于0.05，说明模型的参数都是显著的。

表2 传递函数模型的检验结果Tab. 2 Test result of transfer function model

模型的拟合效果如图1所示。从图1中可以看出，测量得到的腐蚀发展时间与腐蚀深度的散点图与拟合曲线较好吻合，这进一步验证了该模型的拟合优度高。因此，将该模型用于腐蚀损伤后飞机结构件剩余寿命预测是合适的。

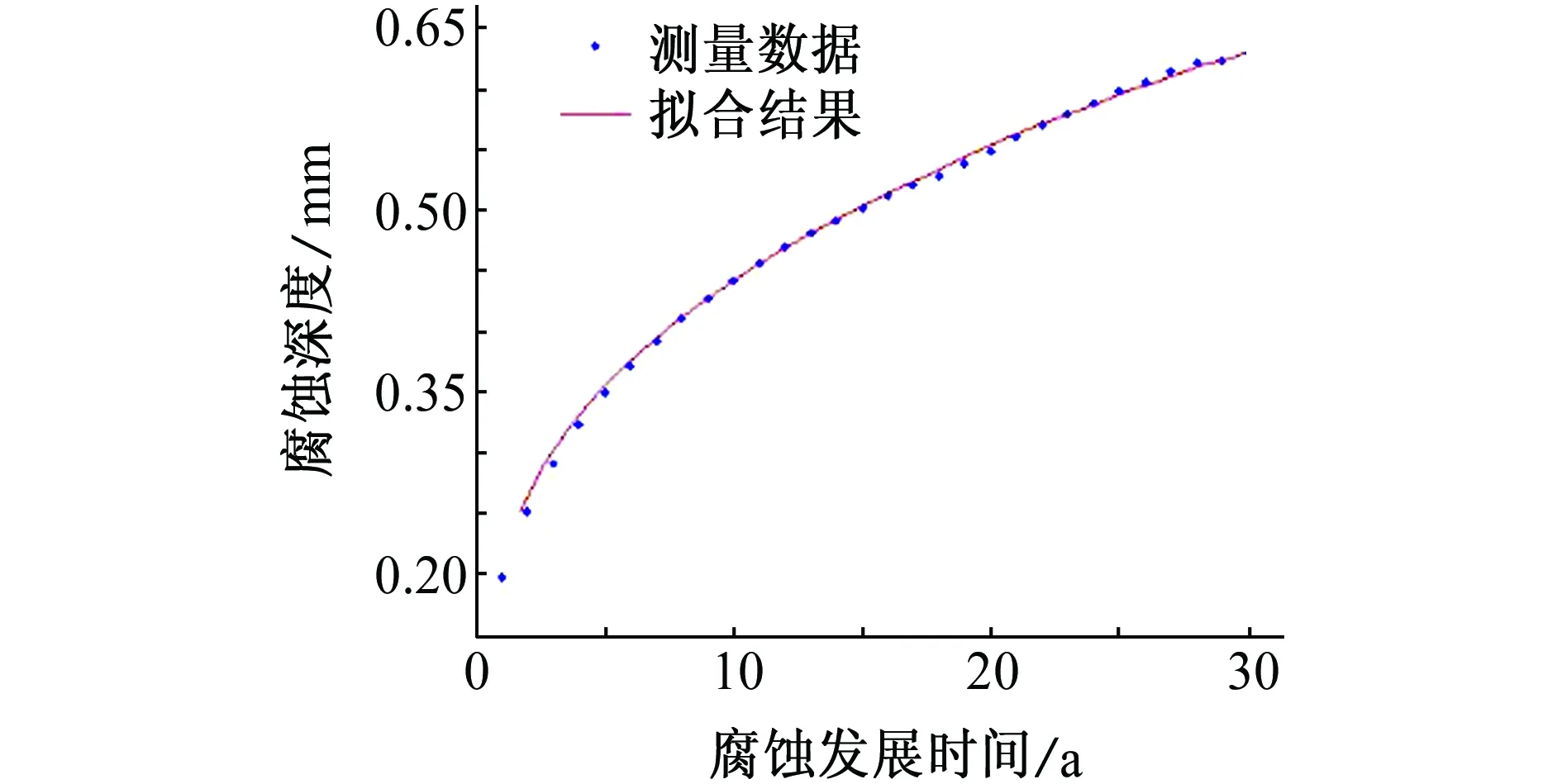
图1 传递函数拟合效果Fig. 1 Transfer function fitting effect

2 飞机结构件腐蚀的可靠性分析

2.1 腐蚀深度的分布形式

腐蚀深度可服从多种形式的分布，如极值I型分布、对数正态分布或威布尔分布。研究表明，最符合腐蚀深度数据分布的是威布尔分布[10]。

由于腐蚀深度一定是非负数，可以判断位置参数为零，本工作采用两参数威布尔分布，其密度函数和分布函数如式(7)和(8)所示。

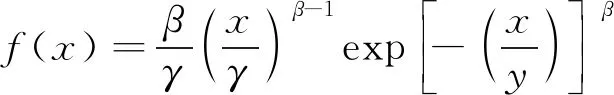
(7)

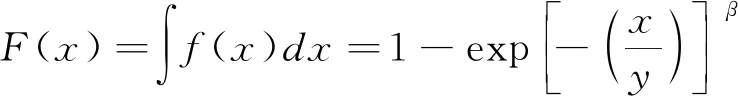
(8)

式中：β为形状参数；γ为尺度参数。

为估计分布参数，需要得到一组样本值。随机选择该飞机隔框上得15个腐蚀坑，测得其腐蚀深度数据，利用样本观测值编写MATLAB程序，采用最大似然法可得β，γ的估计值为1.915 6和1.116 8。

2.2 腐蚀状态划分

AC-121-65 《航空器结构部件持续完整性大纲》通常将飞机结构部件的腐蚀划分为3个等级，根据不同的腐蚀状况采取不同的维修措施。但有时3个等级不能较好地描述飞机结构的腐蚀情况。为此对飞机的结构腐蚀进行更细致的划分[11]，根据维修措施不同将飞机结构件的腐蚀再细分为5个等级，记为S={1,2,3,4,5}，如表3所示。

表3 飞机结构件腐蚀状态划分及相应维修措施Tab. 3 Corrosion state classification of aircraft structural parts and corresponding maintenance

飞机隔框结构的原始厚度一般为3 mm，各腐蚀状态的腐蚀深度和剩余厚度的取值范围如表4所示。

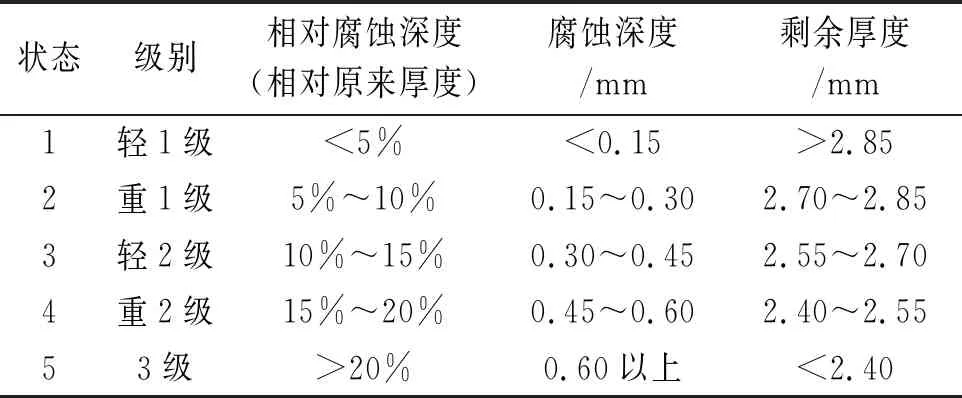
表4 飞机隔框腐蚀状态划分Tab. 4 Corrosion state classification of aircraft frame

2.3 腐蚀的可靠性评估

飞机结构件的剩余寿命不是一个确定的值，而是服从某一分布的随机变量。因此，无法准确衡量飞机结构件的剩余寿命，只能给出飞机结构件的剩余寿命在某一区间的概率值，这也就是可靠性评估的内容。

设飞机结构腐蚀件的失效分布函数F(t′)为

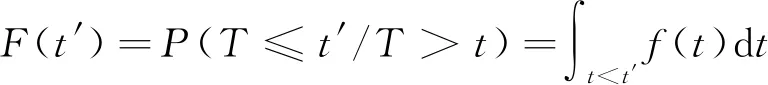
(9)

式中：T为剩余寿命；t′为某时间点；t为当前时刻，即腐蚀发展时间；f(t)为失效分布密度函数，由于腐蚀深度服从威布尔分布，所以假设腐蚀失效分布函数也为威布尔形式。

由腐蚀失效分布可得到腐蚀条件下飞机结构件的可靠度R，如式(10)所示，其实质是飞机结构件剩余寿命T大于某时间点t′的概率P(T>t′)，其值表明了飞机结构件达到了一定使用时间的可能性或可靠性。

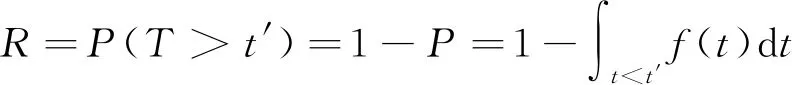
(10)

利用表1所示飞机隔框结构腐蚀深度数据，通过式(6)所示传递函数模型可预测得到腐蚀发展时间，结合式(9)和式(10)，可计算得到不同腐蚀状态对应的飞机结构件剩余寿命和可靠度，结果见表5和表6。

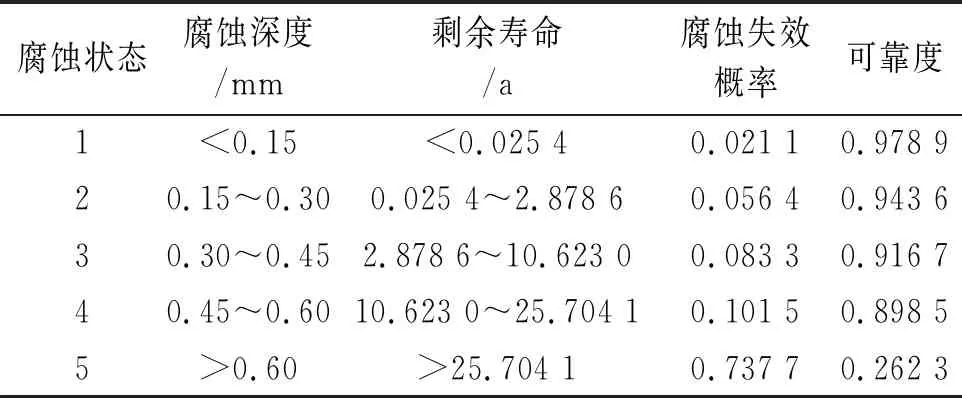
表5 不同腐蚀状态飞机隔框的剩余寿命和可靠性评估Tab. 5 Residual life of aircraft frame in different corrosion status and its reliability assessment

表6 飞机隔框的腐蚀发展时间与可靠性评估Tab. 6 Corrosion development time of aircraft frame and its reliability assessment

每一腐蚀状态都有相应的腐蚀深度与之对应，而腐蚀发展时间又是腐蚀深度的函数，因此表5中每一腐蚀状态都对应一定可靠度的飞机结构件剩余寿命区间。由表5和表6可知,随着腐蚀发展时间的延长，腐蚀等级上升，可靠性显著降低，这与实际相符。

3 结论

(1) 以飞机的隔框结构腐蚀为研究对象，采用传递函数模型获得了飞机结构部件腐蚀发展时间与腐蚀深度的关系，给出了腐蚀结构件的使用寿命预测模型，实例计算结果表明模型拟合优度良好。

(2) 建立了基于腐蚀结构寿命预测的可靠性评估模型，得到了腐蚀发展时间在相应腐蚀状态下的可靠度，其结果与实际相符，可为维修决策和腐蚀防护提供理论支持。