不同X射线残余应力测定方法的原理与应用
程时美
(邯郸市爱斯特应力技术有限公司, 邯郸 056107)
残余应力是第一类内应力的工程名称。残余应力在工件中的分布一般是不均匀的,而且,残余应力会对工件的静强度、疲劳强度、形状尺寸稳定性和耐蚀性等会产生显著的影响[1]。因此,残余应力的测定非常重要。
残余应力测定方法可分为有损检测法和无损检测法。有损检测法是通过机械加工的方式将被测工件的一部分去除,局部残余应力得到释放从而产生相应的应变和位移,根据相关力学原理推算工件的残余应力。常用的有损检测方法有钻孔法与环芯法。无损检测法是利用残余应力会引起材料中某一物理量(如晶面间距、超声波在材料中的传播速率或磁导率)的变化,通过建立此物理量与残余应力之间的关系,测定相关物理量从而计算出残余应力。常用的无损检测方法有X射线衍射法、中子衍射法、磁性法与超声法,其中,X射线衍射法因其原理较为成熟、方法较为完善,是目前在国内外应用最为广泛的方法,其测试设备也越来越完善,既有功能齐全的实验室仪器,也有适用于现场测量的便携式仪器,还有适于特殊场合的专用检测装置。
采用X射线衍射法测定残余应力,最早是由俄国学者阿克先诺夫在1929年提出,把材料的宏观应变等同于晶格应变。1961年德国学者Macherauch基于这个思路研究出sin2ψ法,使得X射线衍射测定残余应力逐渐成为成熟的、具有可操作性的测试技术。
X射线衍射测定残余应力技术经过60 a的发展,开展出多种不同的测量方法。目前X射线衍射测定残余应力技术主要有sin2ψ法与cosα法两种。
1 X射线衍射残余应力测定方法分类
为了掌握X射线衍射残余应力测定技术,有必要其方法进行归纳。
(1) X射线衍射残余应力测定方法可分为sin2ψ法、cosα法。
(2) sin2ψ法按照残余应力计算方法分类,可分为2θ法、d值法、应变法。
(3) sin2ψ法按ψ与2θ的几何关系分类,可分为同倾法、侧倾法。
(4) 按X射线管、计数管扫描方式可分为固定ψ0法,固定ψ法。
(5) 侧倾法又可分为标准的侧倾法、修改的侧倾法、侧倾固定ψ法。
(6) 测定剪切应力τφ采用的正负ψ测定法。
(7) X射线衍射法一般是测定指定点指定方向的应力,也有指定点的主应力测定法。
(8) 摆动法可分为ψ0摆动法、ψ摆法、德拜环摆动法、φ角摆动法和X/Y往复平移法等。
(9) 从衍射几何分类,有聚焦法、准聚焦法和平行光束法。
2 X射线衍射残余应力测定的sin2ψ法
应力是通过应变来进行测定的,对于多晶体材料而言,残余应力所对应的应变被认为是相应区域里晶格应变的统计结果,因此依据X射线衍射原理测定晶格应变,即可计算残余应力。
材料的残余应力与宏观应变相对应,宏观应变被认为等同于晶格应变,晶格应变即晶面间距的相对变化,而晶面间距的变化可以通过衍射装置依据布拉格定律求出,这便是X射线衍射残余应力测定法的完整思路。
2.1 布拉格定律
当一束具有一定波长λ的X射线照射到多晶体上时,会在一定的衍射角2θ上接收到反射的X射线强度极大值(即衍射峰),这便是X射线衍射现象,如图1所示。X射线波长λ、衍射晶面间距d和布拉格角θ之间满足公式(1)。
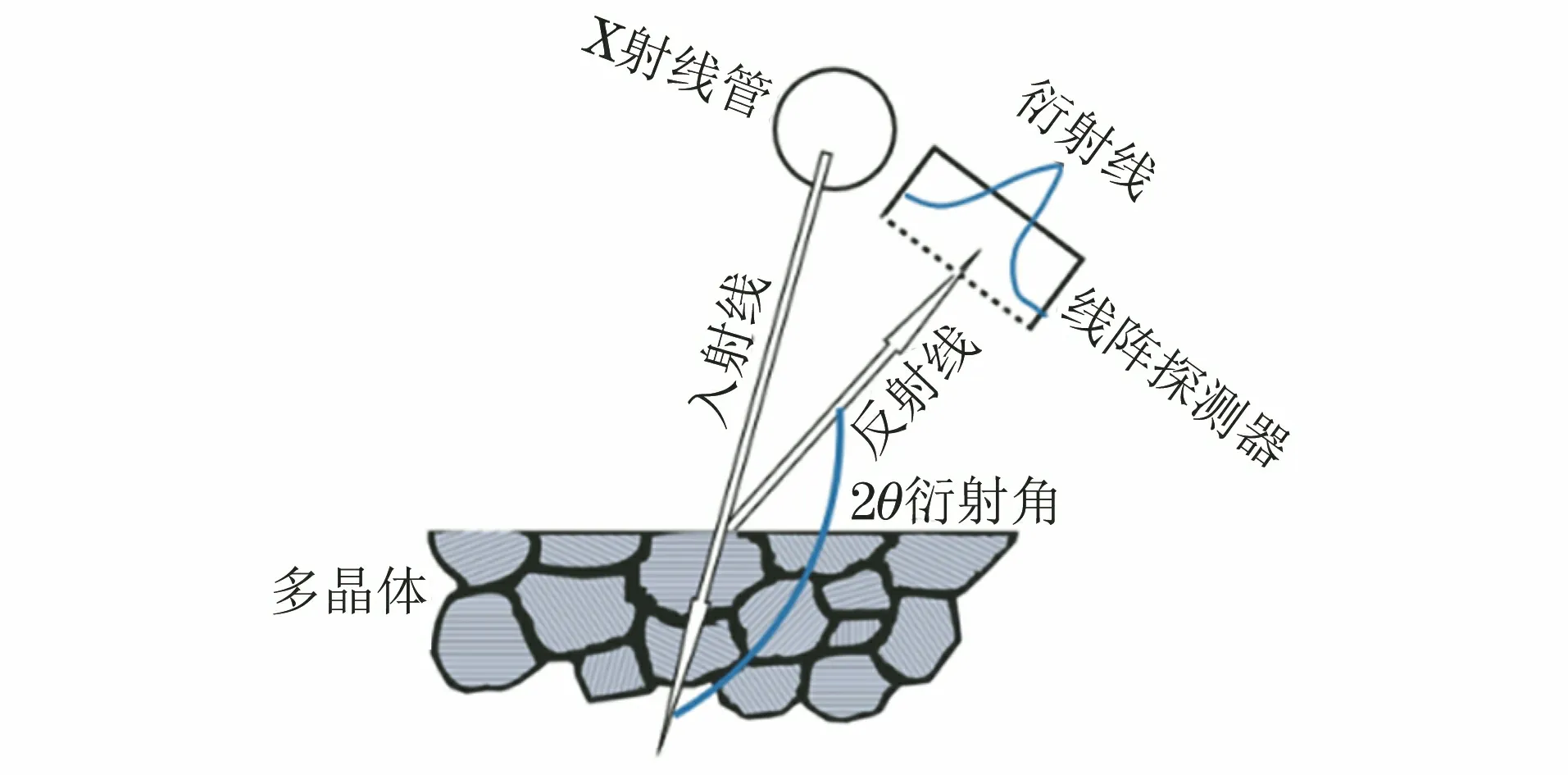
图1 X射线衍射几何图Fig.1 X-ray diffraction geometry diagram
2dsinθ=nλ(n=1,2,3,…)
(1)
在X射线衍射残余应力分析中,选用合适靶材的X射线管,即选定合适的波长λ,通过衍射装置测定衍射角2θ,就可以计算出相应晶面的晶面间距d。
2.2 晶面衍射方位角ψ
依据光学的反射定律,参与衍射的晶面,其法线必定处于入射线与反射线的角平分线方位上,如图2所示。衍射晶面法线与试样表面法线的夹角即为衍射晶面法线方位角,通常用ψ表示。
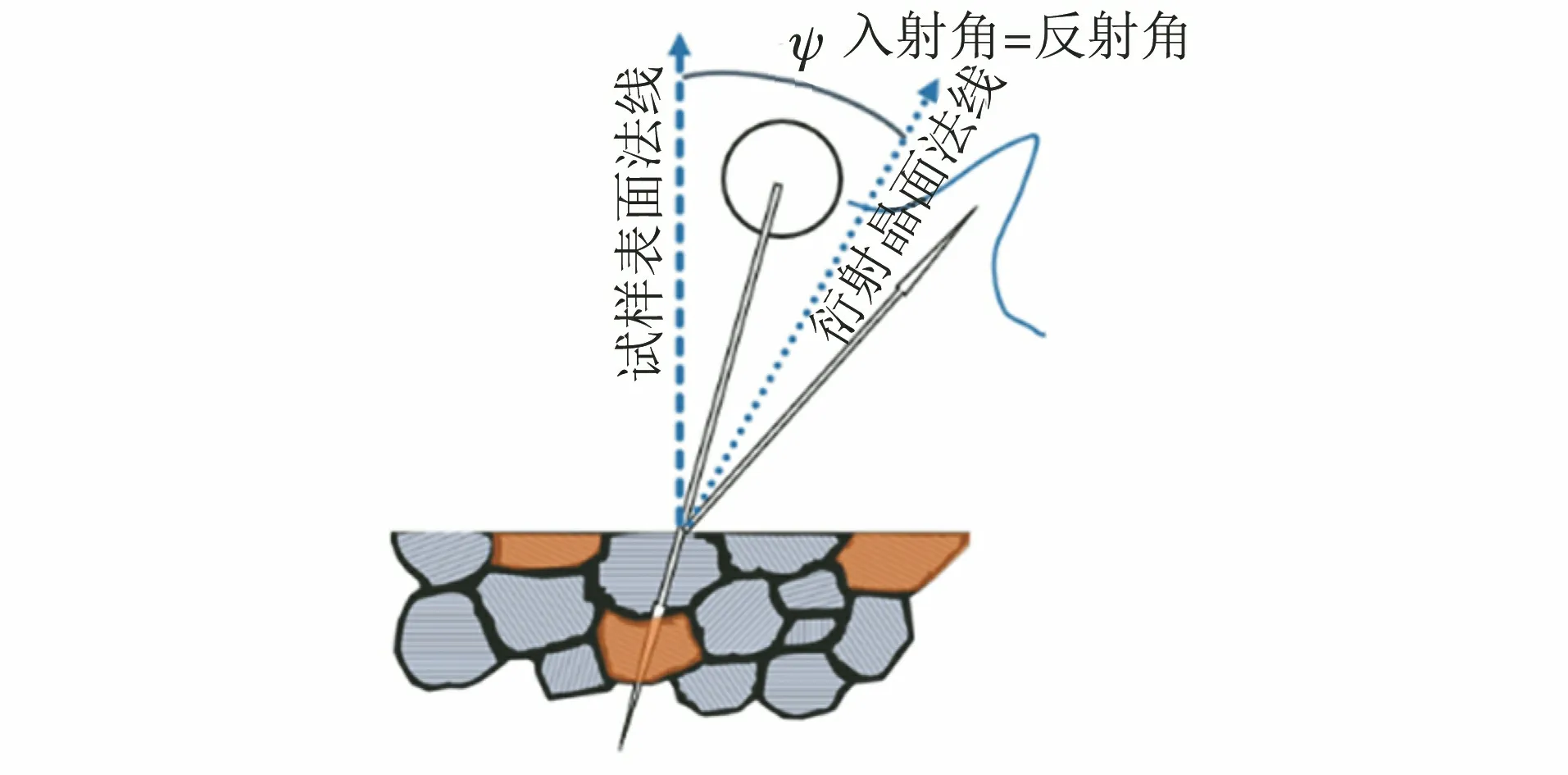
图2 X射线衍射晶面方位角ψ示意Fig.2 Schematic diagram of azimuth angle ψ of X-raysdiffraction crystal plane
依据布拉格定律,可以测定指定ψ所对应方位上的晶面间距dψ。如果已知无应力状态的晶面间距d0,便可以测定指定方位上的晶格应变εψ。
2.3 sin2ψ法的适用范围
S1,S2与S3为试样表面坐标轴,S1由笔者定义。
sin2ψ法由德国学者马赫劳赫于1961年提出,图3为X射线衍射残余应力测定坐标系统。图3中:S3为垂直于试样表面的坐标轴(试样表面法线);O为试样表面上的一个点;OP为空间某一方向;φ为Sφ与S1的夹角;L1,L2,L3为实验室坐标系统;L3为确立在OP方向上;Sφ为OP在试样平面上的投影所在方向。为了测定试样表面O点Sφ方向的应力σφ,最直接的办法是求出O点Sφ方向的应变,然后根据胡克定律就可以计算出应力σφ。然而,X射线衍射残余应力测定法几乎无法得到垂直于试样表面的晶面间距,要测定该材料无应力状态下的晶面间距d0也十分困难。于是,选取试样表面O点以OP为法线的{hkl}晶面,并以图3中的φ、ψ角表征OP的方向,OP在试样表面的投影OSφ即为待测应力方向。
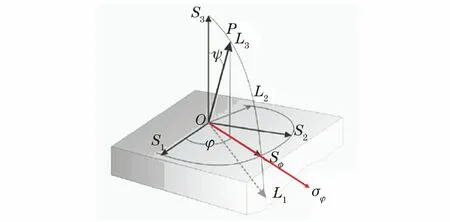
图3 X射线衍射应力测定坐标系统Fig.3 X-ray diffraction stress measurement coordinate system
依据广义胡克定律,这些晶面的应变是由O点的应力张量决定的,并且与φ、ψ的正余弦、材料的杨氏模量和泊松比等参量密切相关。因此,有可能依据这些的关系求得O点的三维应力,包括应力σφ。由弹性力学可以导出OP方向上的应变的表达式。对于大多数材料和零部件来说,X射线穿透深度只有几微米至几十微米,因此通常假定σ33=0。所以,OP方向的应变如式(2)所示。
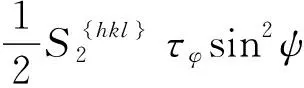
(2)
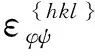
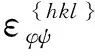
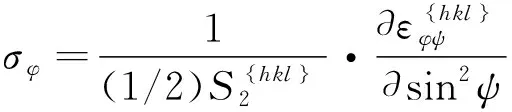
(3)
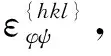
sin2ψ法公式是基于布拉格定律和弹性理论推导出来的,弹性理论所涉及的对象被假定为均匀、连续、各向同性的介质。对于多晶金属材料来说,只有晶粒细小,没有织构,才近似满足这样的假定。
图4分别为各向同性材料、存在应力梯度或成分梯度的材料、存在剪切应力的材料、存在织构的各向异性材料的εn与sin2ψ的函数关系曲线。
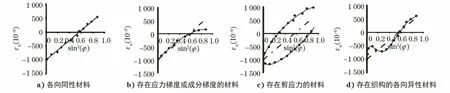
图4 不同材料的sin2ψ曲线Fig.4 The sin2ψ curve of different materials:a) isotropic material; b) material with stress gradient or composition gradient; c) material with shear stress; d) anisotropic materials with texture
如图4c)所示,如果出现剪切应力τ13≠0,τ23≠0,sin2ψ曲线出现±ψ分叉的情况,使用测得的一系列±ψ角上的应变数据ε﹢ψ和ε﹣ψ,可以求出σφ和τφ,如式(4)和式(5)所示。
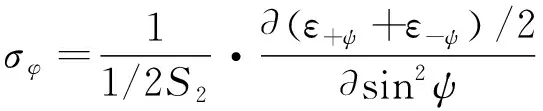
(4)
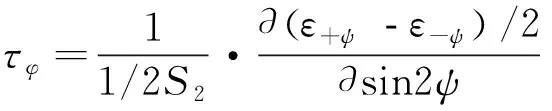
(5)
需要说明的是图4c)所示的sin2ψ曲线真正出现±ψ分叉的情况是很罕见的。因为,衍射用的X射线对被测材料的穿透能力极低,大多在几微米或十几微米的深度。因此,可以认为垂直于材料表面方向的应力分量均为零。只有在特殊加工(如强力的、大切削量的磨削)的条件下,致使主应力平面偏离试样表面,才可能出现τ13≠0,τ23≠0的情况。通常出现±ψ分叉情况,拟合曲线往往不具备椭圆属性,其实质应该是测角仪±ψ机构的系统误差造成的,因此无需过分强调椭圆拟合的必要性。
综上所述,X射线衍射残余应力测定的实际可操作过程就是选择若干ψ角(或若干对±ψ角)分别测定衍射角2θφψ,然后进行计算。关于如何安排ψ平面和2θ平面的空间几何关系、如何获取衍射曲线、如何进行计算等方面,学者们研究出了许多方法。
3 真应变法、2θ法和d值法
使用X射线衍射装置测得衍射角2θφψ,根据布拉格定律求得与之对应的晶面间距为dφψ,则晶格应变εφψ可用晶面间距来表示,如式(6)所示。
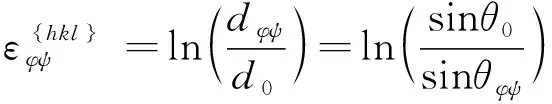
(6)
将真应变直接代入式(3)、式(4)、式(5)计算应力,就是真应变法表达式。采用真应变法,无需d0和θ0的精确值。在大多数情况下采用真应变法具有显著优越性。
计算应变也可以使用近似方程,如式(7)和式(8)所示。
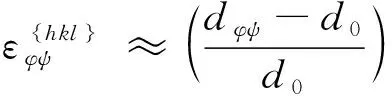
(7)
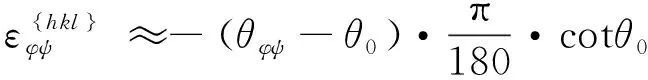
(8)
2θ法的计算公式如式(9)所示。
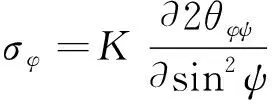
(9)
式中:K为应力常数,其计算公式如式(10)所示。
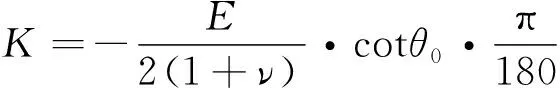
(10)
式中:ν为材料的泊公比。
对于某些材料,随着化学成分的不同,θ0变化很大,使用应力常数,结果会出现较大偏差。例如,镍基高温合金,随着化学成分的不同,采用锰靶(311)晶面,其名义衍射角为152°~162°,无法确定应力常数K,所以不能采用2θ法,只能采用真应变法。真应变法已经载入欧盟标准 EN 15305-2008Non-destructivetesting——TestmethodforresidualstressanalysisbyX-raydiffraction和GB/T 7704-2017《无损检测 X射线应力测定方法》,XL-640型国产应力仪把真应变法列为默认应力计算方法,同时可以选择2θ法进行计算。
4 同倾法与侧倾法
同倾法是2θ平面与ψ平面(应力方向平面)相重合的测量方法,如图5所示。图5中:D为X射线探测器;X为X射线管;ON为衍射晶面法线。最早的应力仪是从当时的衍射仪演化而来,故采用同倾法,其所用的设备结构较为简洁,便于实际操作。在测试中对测角仪至试样测试点之间的距离(即标定距离)的误差有较大的宽容度,因此,测试结果重复性较好。采用同倾法,X射线入射角ψ0是显性的,而ψ角通过计算才能求出,如式(11)和式(12)所示。
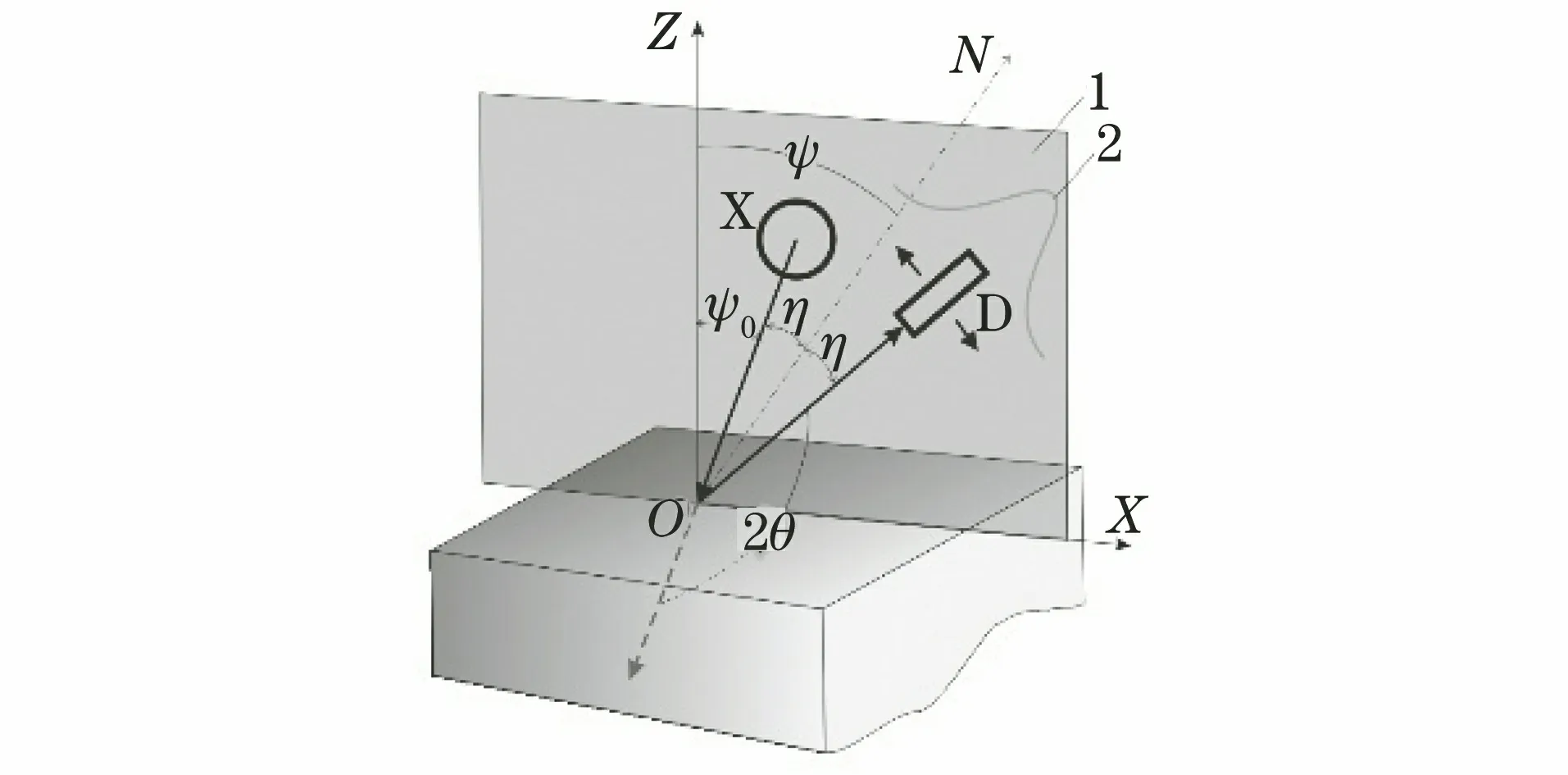
图5 同倾法几何示意Fig.5 Geometry schematic diagram of same tilt method
ψ=ψ0+η
(11)
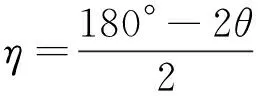
(12)
在实际工件的应力测试中,遇到测试点位于类似较浅沟槽部位的时候,测角仪测试空间受限,比较适合采用同倾法。
侧倾法是2θ平面与ψ平面(应力方向平面)相互垂直的测量方法,,如图6所示,该方法由德国学者沃尔夫斯提克提出。
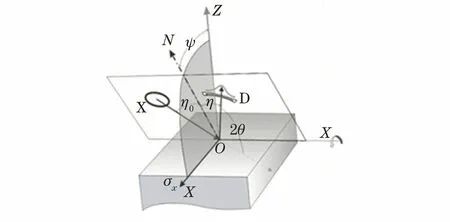
图6 侧倾法几何示意Fig.6 Geometry schematic diagram of roll method
侧倾法(χ法)的特点是衍射峰的吸收因子作用很小,有利于提高测定精度。2θ范围与ψ范围可以根据需要充分展开,对于某些材料可以使用峰位较低(如峰位低于145°)的衍射线测定应力。但是,由于该方法的2θ平面与ψ平面互相垂直,需要的是一个立体的空间,难以适用于某些空间狭小部位的测定。
某国外公司的应力仪产品采用的是修改后的侧倾法,采用双探测器,其几何布置示意如图7所示。图7中:DR为右X射线探测器;2θR为右探测器测试的衍射角;DL为左X射线探测器;2θL为左探测器测试的衍射角;ONR为右衍射晶面法线;ONL为左衍射晶面法线。该方法中的2θ平面与ψ平面并不是相互垂直的。早在1977年1月中科院金属研究所李家宝就提出了这种测试方法和计算公式,如式(13)和式(14)所示。
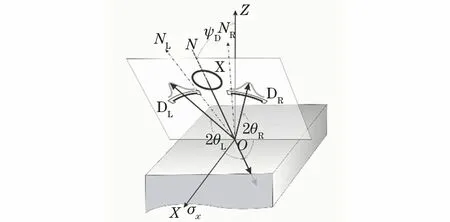
图7 修改后的侧倾法几何示意Fig.7 Geometry schematic diagram of modified roll method
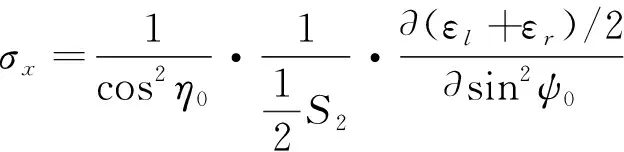
(13)
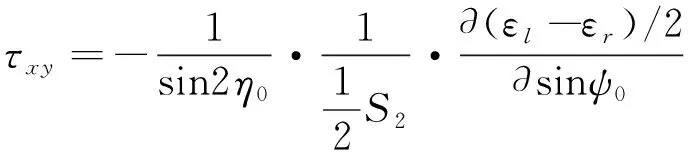
(14)
侧倾法又分为固定ψ0法和固定ψ法,固定ψ法又因原理准确、实用效果好而优于前者。将两种方法结合,即在侧倾的条件下实施固定ψ法便会使吸收因子恒等于1。也就是说,不论衍射峰是否漫散,它的背底都不会倾斜,峰形基本对称,而且在无织构的情况下峰形及强度不随ψ角的变化而变化。显然,这个特点对提高测量精度是十分有利的,侧倾固定ψ法是很理想的一种测量方法。
5 摆动法
摆动法是在探测器接收衍射线的过程中,以每一个设定的ψ角(或ψ0角)为中心,使X射线管和探测器在ψ平面内左右回摆一定的角度(±Δψ或±Δψ0)的应力测定方法。这种方法增加了材料中参加衍射的晶粒数,是解决粗晶材料应力测定问题的近似处理方法。基于这样的思路,还可以采取φ角摆动法和X/Y平移摆动法,甚至可以组合不同的摆动方法进行测试。
6 X射线衍射残余应力测定cosα法
2012年日本PULSTEC公司首次推出基于二维探测器技术的应力仪,该仪器采用单次入射方式,利用二维探测器采集X衍射线,可于短时间内采集到测试点的德拜环信息。德拜环上各点对应的晶面法线与试样表面法线形成的ψ角不在一个平面内,所以无法用sin2ψ法计算应力,从而使用α角,这就是所谓的cosα法,如图8所示。
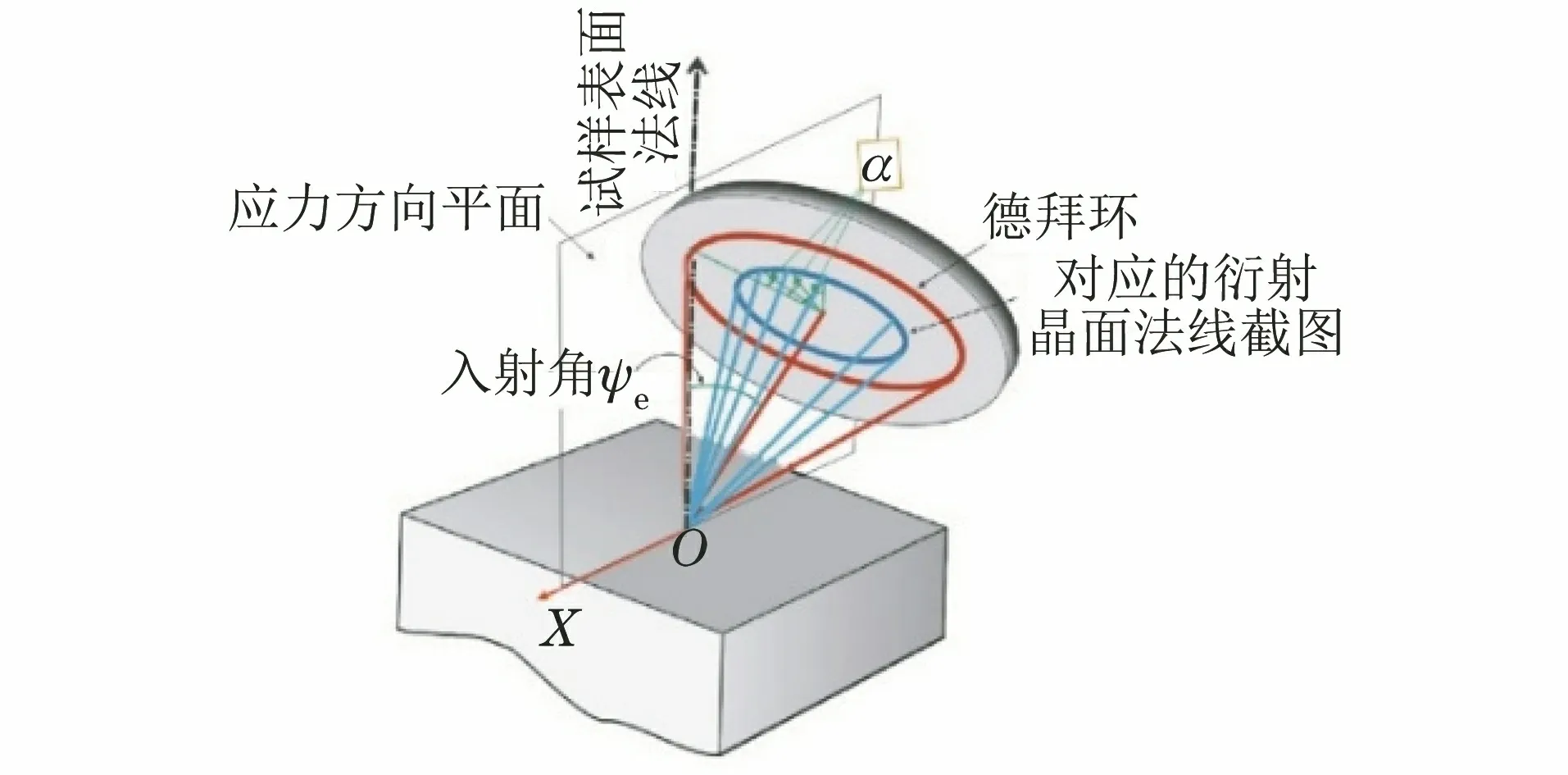
图8 cosα法几何示意Fig.8 Geometry schematic diagram of cosα method
该测试方法比较适用于大型钢结构件的表面应力测试。对于测试粗晶粒材料或存在织构的材料而言,该仪器的使用具有局限性。欧盟标准BS EN 15305:2008Non-destructivetesting——TestmethodforresidualstressanalysisbyX-raydiffraction附录中F3.8二维探测器的使用一节中写道:理论表明一次测量就能得到精确的应力分量,但实际上由于ψ的测量范围太小而无法给出合理的精确值。正因如此,cosα法计算应力暂时没纳入国标GB/T 7704-2017、欧盟标准BS EN15305:2008、美标ASTM E915-2010StandardTestMethodforVerifyingtheAlignmentofX-RayDiffractionInstrumentationforResidualStressMeasurement等X射线衍射残余应力检测方法标准中。
cosα法基于弹性力学原理,如式(15)和式(16)所示。
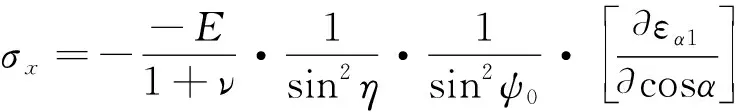
(15)
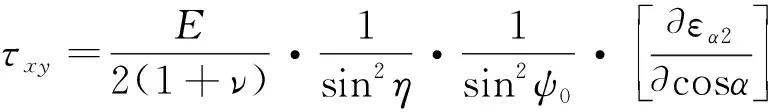
(16)
图9“全二位探测器”ψ角最大采集范围(入射角为45°)见图8,α角在德拜环平面上,即德拜环上每个点的圆心角。对于试样表面O点而言,德拜环上各点的2θ角,都会因OX方向上的应力而有所变化,也可以认为各点都对应一定的晶格应变。然而,这些应变都只是应力方向平面上对应ψ方向上应有应变的一个分量。尽管德拜环上可以选取很多数据点,对应的晶面法线有很多条,但是其ψ角范围却很小。以α-Fe(211)晶面CrKα辐射为例,若ψ0为35°,则ψ在23°至47°范围内,其sin2ψ值落在图9的方框里,而且不包含-ψ对应的应变。
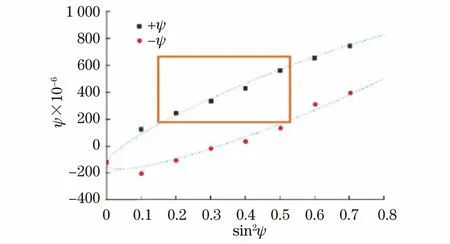
图9 sin2ψ曲线中cosα法数据点的位置Fig.9 Location of data points of cosα method in sin2ψ curve
其实X射线衍射残余应力测定的两种方法基于的力学原理是一致的。将应变张量在空间角度上的进行变换,cosα法所采用的α角完全可以与ψ角进行相互换算。cosα法其实就是近似处理的sin2ψ法(如欧盟标准BS EN15305:2008中修正的χ法)。
7 不同仪器测定热轧钢板的残余应力对比
通常使用的热轧钢板,一般可以认为不存在织构,实际上由于多种因素的作用,钢板某些部位会存在某种程度的织构。在此情况下,多数用户仍然倾向于采用X射线衍射法测定其残余应力。
选取一块存在织构的热轧钢板,分别使用日本PULSTEC品牌的μ-X360S型应力仪、加拿大 PROTO品牌LXRD型应力仪、法国MRX品牌 X-RAYBOT型应力分析机器人和中国爱斯特品牌XL-640型应力仪,测定Z方向的Z(0)、Z(1),Z(2),Z(3),Z(4),Z(5),Z(-1),Z(-2),Z(-3),Z(-4),Z(-5)点的残余应力。测试条件与测试结果分别见表1与表2,各个仪器测定Z(0)点残余应力的试验报告如图10~13所示。
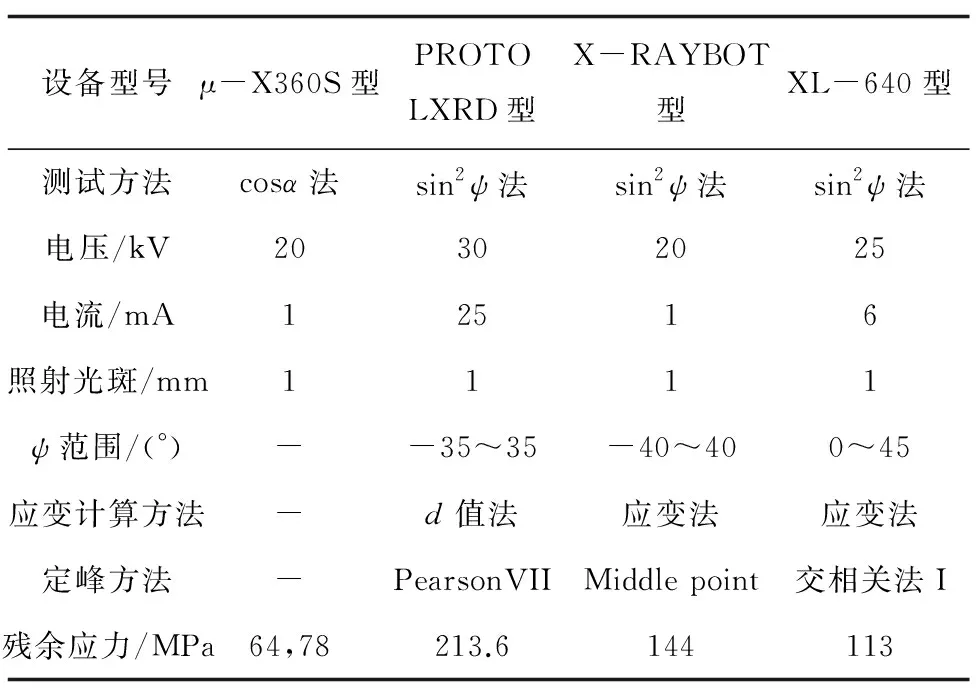
表1 不同应力仪测定热轧钢板残余应力的测试参数Tab.1 Test parameters for measuring residual stress of hot-rolled steelsheets by different stress meters
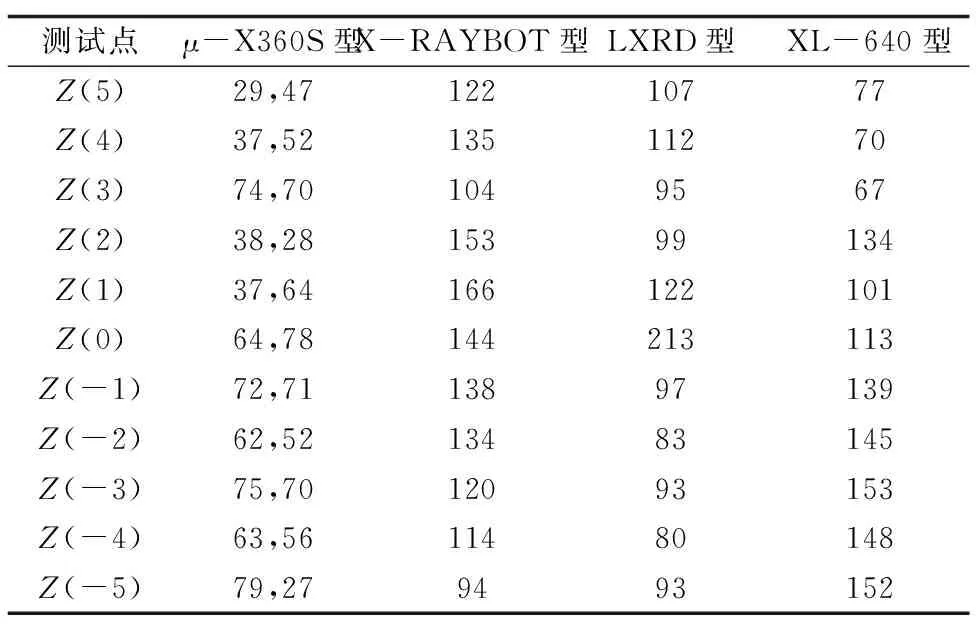
表2 不同应力仪测得的热轧钢板的残余应力Tab.2 Residual stress of hot-rolled steel plate measuredby different stress meters MPa
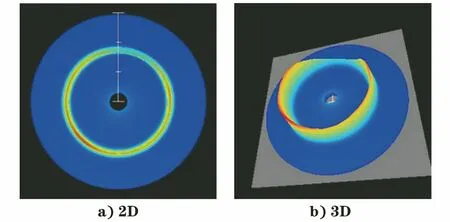
图10 采用μ-X360S型应力仪测定Z(0)点的德拜环Fig.10 Debye ring at point Z(0) measured by μ-X360S stress meter:a) 2D; b) 3D

图11 采用PROTO LXRD型应力仪测定Z(0)点的2θ-sin2ψ曲线Fig.11 2θ-sin2ψ curve at point Z(0) measured byPROTO LXRD stress meter
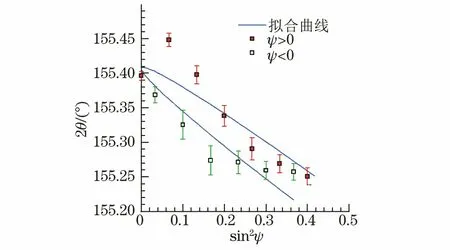
图12 采用X-RAYBOT型应力仪测定Z(0)点的2θ-sin2ψ曲线Fig.12 2θ-sin2ψ curve at point Z(0) measured byX-RAYBOT stress meter
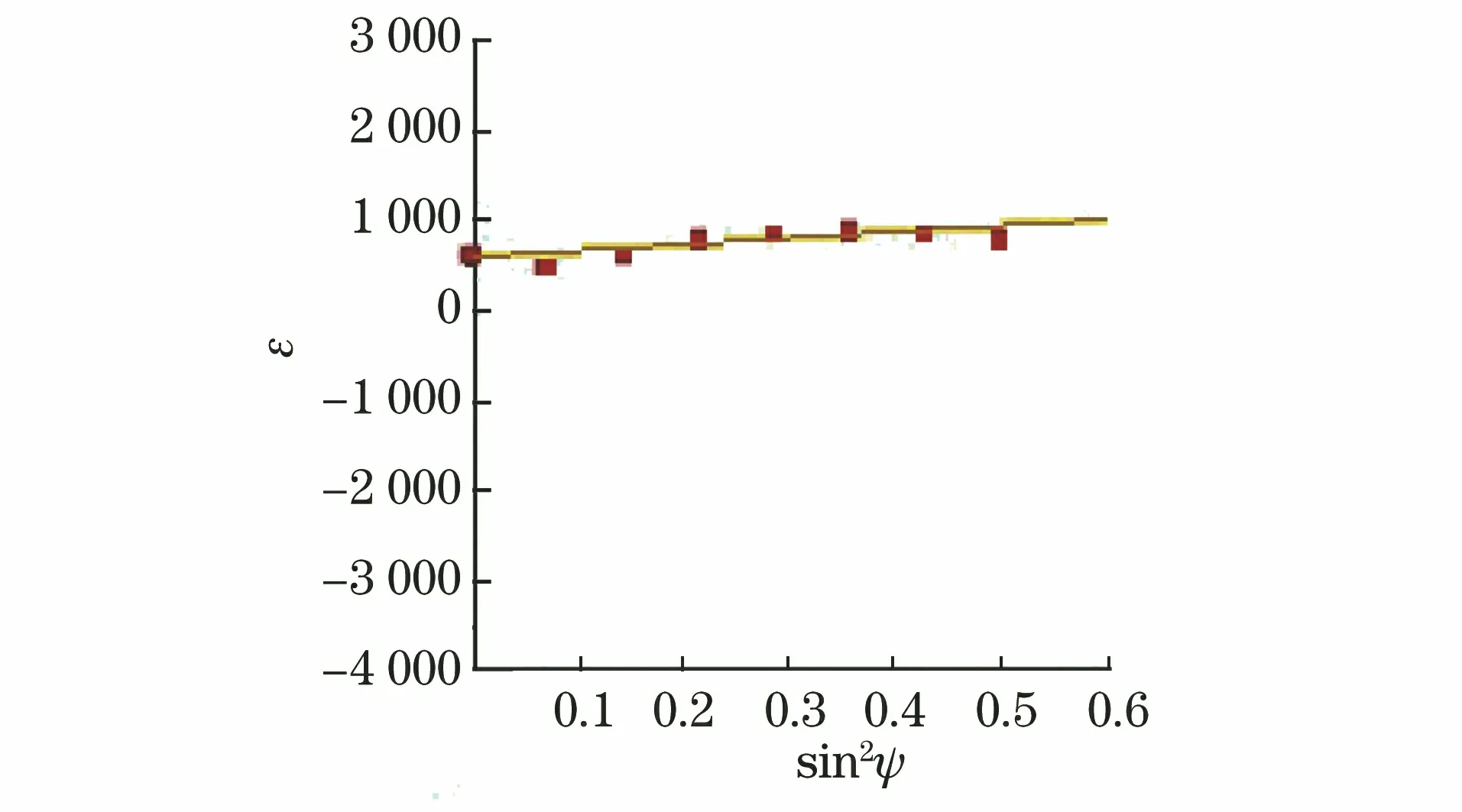
图13 采用XL-640型应力仪测定Z(0)点的ε-sin2ψ曲线Fig.13 ε-sin2ψ curve at point Z(0) measured byXL-640 stress meter
cosα法测得的残余应力比sin2ψ法测得的残余应力小。对于Z(0)测试点,采用XL-640型应力仪,按照sin2ψ等间距的原则,在0°~45°范围内选取8个ψ角,结果如图14~15所示,可以看出由于材料存在织构,其sin2ψ曲线呈现“震荡”型。
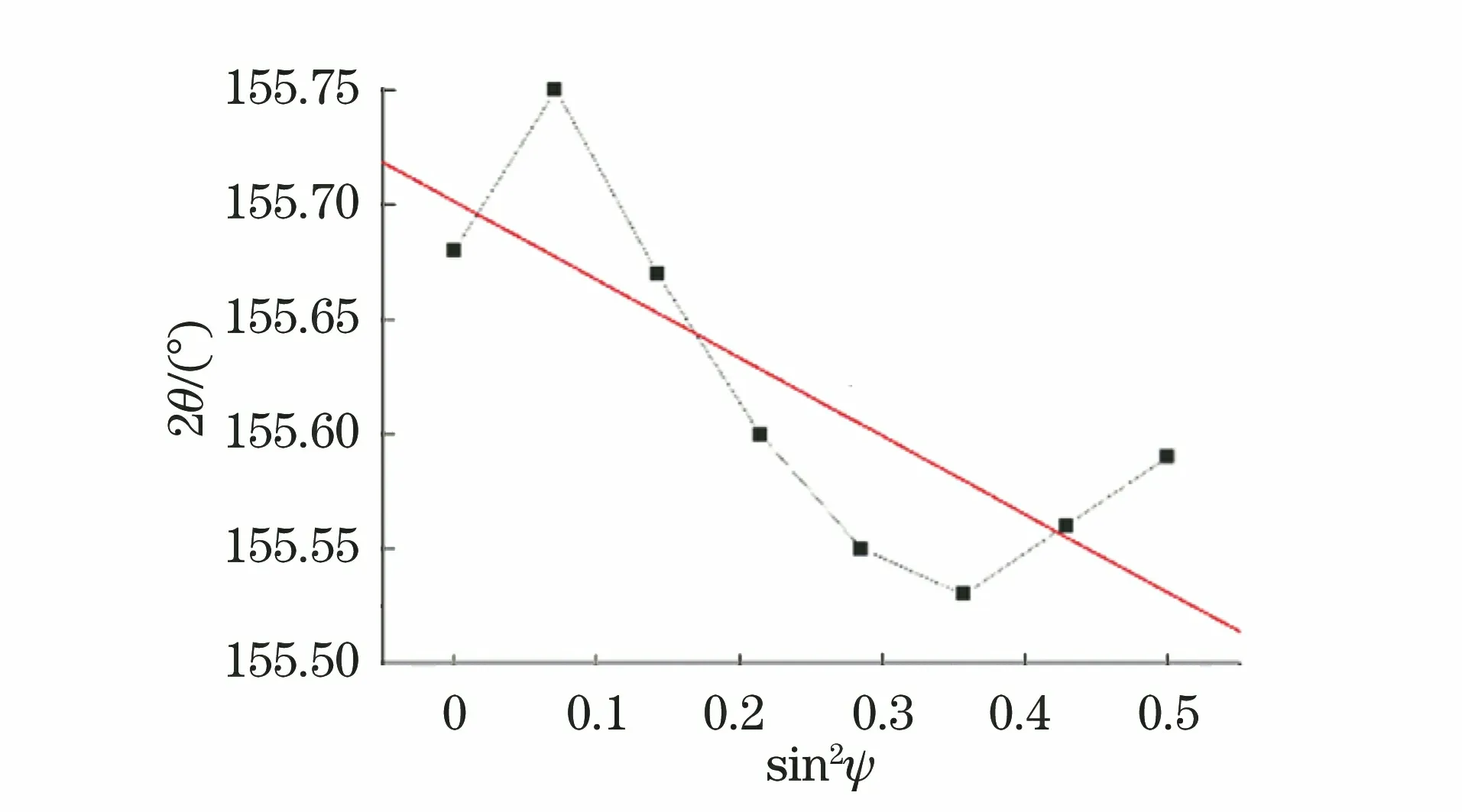
图14 采用XL-640型应力仪测定Z(0)点的2θ-sin2ψ曲线的拟合结果Fig.14 Fitting result of 2θ-sin2ψ curve at point Z(0)measured by XL-640 stress meter
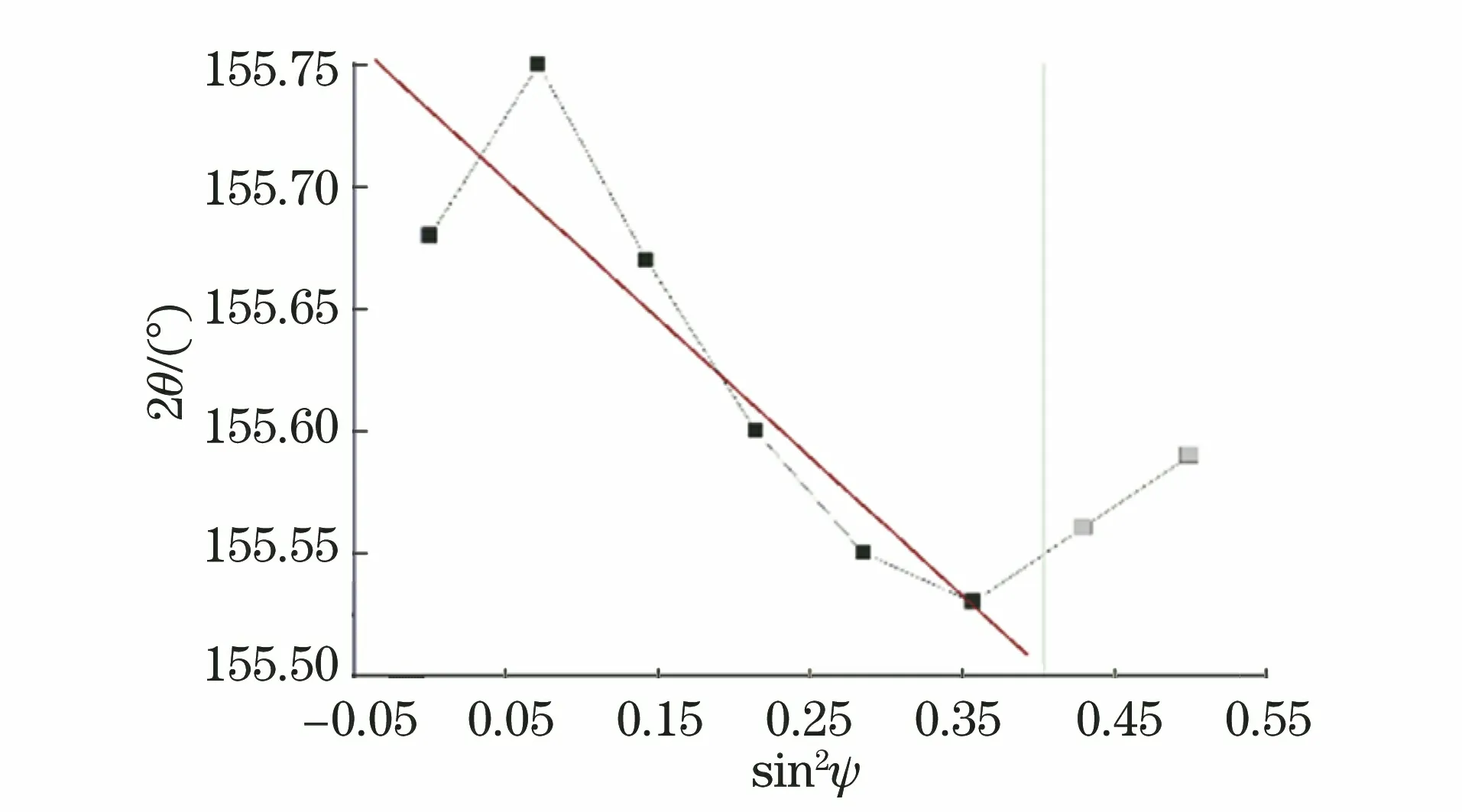
图15 采用μ-X360S型应力仪测定Z(0)点的2θ-sin2ψ曲线的拟合结果Fig.15 Fitting result of 2θ-sin2ψ curve at point Z(0)measured by μ-X360S stress meter
图13中的sin2ψ曲线纵坐标为应变ε,将纵坐标改为2θ后,进行线性拟合,结果如图14所示,得到的拟合直线的斜率M为-0.355,残余应力σ为113 MPa。
采用μ-X360S型应力仪所选的ψ范围,相当于屏蔽前两个2θ值,再进行直线拟合,结果见图15,该拟合直线的斜率M为-0.216,σ为68.69 MPa。由于前两个较高2θ值的缺失,拟合直线的斜率M和残余应力σ均下降明显。采用XL-640型应力仪测试数据进行直线拟合得出的残余应力与采用μ-X360S型应力仪测得的残余应力(64 MPa)非常接近。
采用PROTO LXRD型应力仪测试所选的ψ范围,将图14中的最后三个2θ值屏蔽,再进行线性拟合,结果如图16所示,该拟合直线的斜率M为-0.688 8,σ为219 MPa。可见,由于屏蔽了最后三个较低2θ值,拟合直线的斜率M和残余应力σ均显著升高,且该残余应力与采用PROTO LXRD型应力仪测得的残余应力(213.6 MPa)也非常接近。
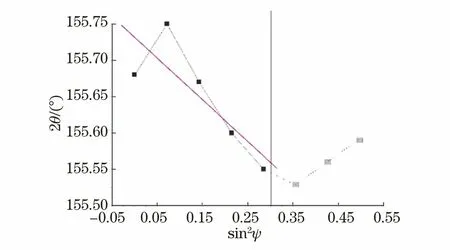
图16 采用PROTO LXRD型应力仪测定Z(0)点的2θ-sin2ψ曲线的拟合结果Fig.16 Fitting result of 2θ-sin2ψ curve at point Z(0) measuredby PROTO LXRD stress meter
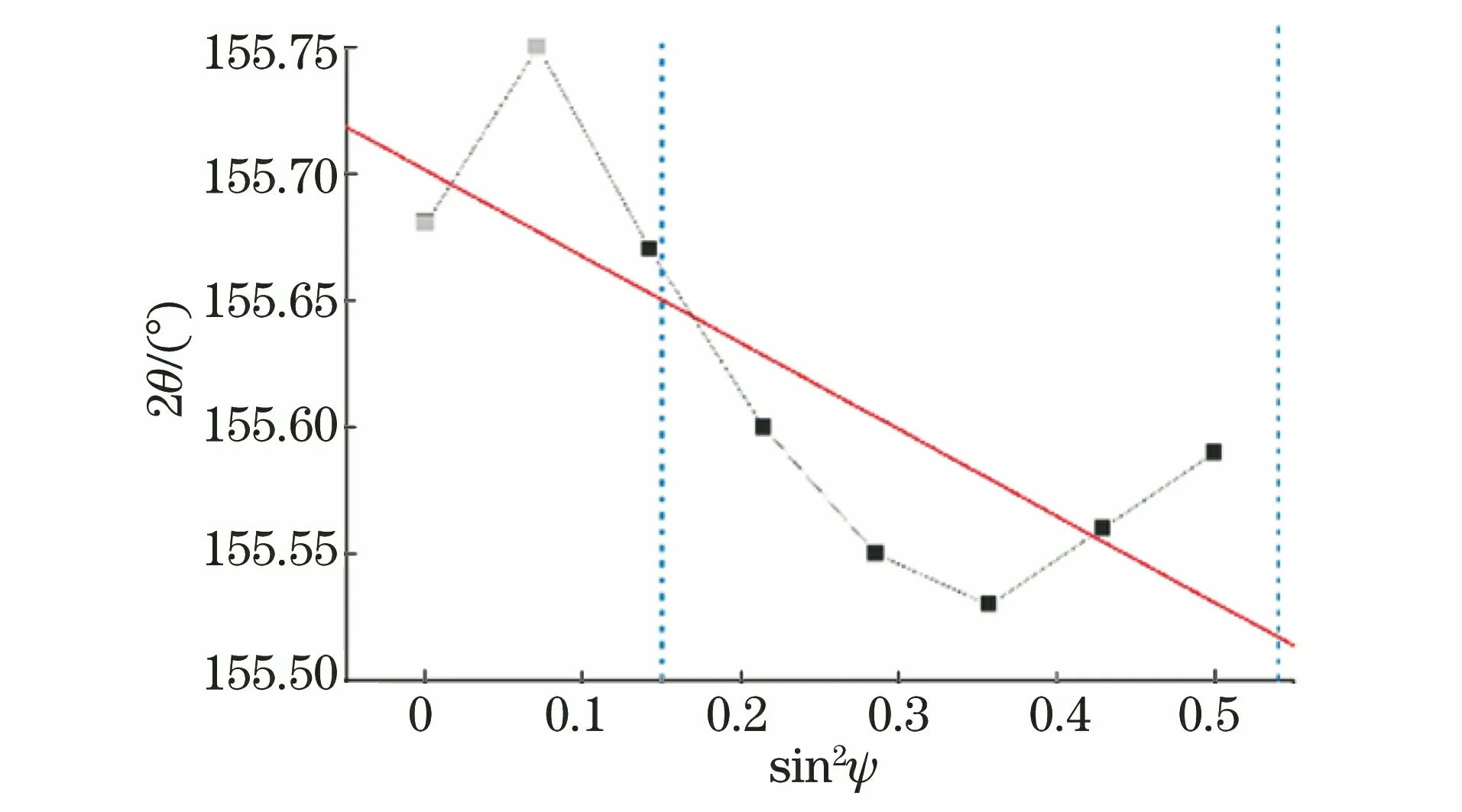
图17 采用X-RAYBOT型应力仪测定Z(0)点的2θ-sin2ψ曲线的拟合结果Fig.17 Fitting result of 2θ-sin2ψ curve at point Z(0) measuredby X-RAYBOT stress meter
由图12可知,采用X-RAYBOT型应力仪得出Z(0)点的sin2ψ最大值为0.4,根据其选定的ψ范围,将图14中的最后两个2θ值屏蔽,然后进行线性拟合,结果见图19,该拟合直线的斜率M为-0.568,σ为180 MPa,该残余应力与X-RAYBOT型应力仪测得的残余应力(144 MPa)相差不大。由于缺失40°之后对应的2θ,使拟合直线的斜率M增大,残余应力σ偏高。
由于材料存在织构,其sin2ψ曲线呈震荡型,选取的ψ角范围不同,得到的拟合直线的斜率和残余应力存在明显差异。在未知材料是否存在织构、晶粒是否粗大的情况下,不可选取较小的ψ范围和较少的ψ站数进行残余应力测定,否则会带来较大的测量误差。
对于sin2ψ曲线呈震荡型的织构材料,采用线性拟合未必是合理的,实际测量过程中,人们通常采用线性拟合的方式对这种震荡和测量误差引起的波动进行处理。关于ψ的范围,最大达45°也未必合理,如果可以忽略穿透深度的影响,采用更大的ψ角会更有利于获得较为正确的结果。
对于粗晶粒材料或存在织构的材料而言,尽量扩大ψ角的设置范围,可以通过±ψ角的测量来消除ε-sin2ψ非线性分布的影响[2]。对于最小二乘法拟合回归直线而言,若自变量的间距越大(ψ范围越大),测量的数据越多(ψ站数越多),则拟合所得到的直线的准确度越高,测试得到的数值就越可靠。也可以通过增加X射线的照射面积,或是采用摆动法增加参与衍射晶粒的数量来提高测试精度。
8 结论
(1) sin2ψ法可以采用选取较大的ψ范围和较多的ψ站数进行残余应力测定,从而提高测试精度。cosα法采用单次曝光,ψ范围不够大会造成较大的测量误差,具有局限性,有待于进一步完善。
(2) 在基于sin2ψ法原理的测量方法中,与同倾法相比,侧倾法具有明显的优越性。在被测点所处空间条件允许的前提下,应尽量采用侧倾法。对于某些零件的沟槽部位的残余应力测定,通常采用同倾法。
(3) 在残余应力的计算方法中,可首选真应变法。
(4) sin2ψ法作为一种标准的方法,ψ角的设置最好采用sin2ψ值等分法,尽量多选择几个ψ角进行测量。

