谱域光学相干层析系统的色散补偿技术研究

姜盼秋，汪平河

谱域光学相干层析系统的色散补偿技术研究

姜盼秋，汪平河*

电子科技大学光电科学与工程学院，电子薄膜与集成器件国家重点实验室，四川 成都 611731

对谱域光学相干层析系统(SD-OCT)采用色散补偿方法进行优化，是提高系统成像质量的重要方式。本文提出了一种基于数值多项式拟合的色散补偿方法。该方法通过提取干涉信号的相位并解包裹，利用数值多项式对解包裹后的相位进行拟合，然后根据拟合出的高阶色散因子对干涉信号做相位补偿。本文利用SD-OCT系统测量出不同光程差位置处的轴向分辨率和信噪比，通过比较分析色散补偿前后系统的轴向分辨率及信噪比，来验证该方法的有效性和可靠性。结果表明，本文设计的色散补偿技术可以使系统具有良好的轴向分辨率，三阶多项式拟合相位的色散补偿方法在约1.5 mm的成像深度范围内有明显的优化效果。

谱域光学相干层析系统；色散补偿；分辨率；信噪比；成像质量

1 引 言

光学相干层析(Optical coherence tomography，OCT)技术是一种重要的断层成像技术，能够对生物组织和材料内部微观结构进行横截面和三维成像，具有分辨率高、成像速度快、非接触以及可实时成像等优点[1-2]。OCT通过测量生物组织后向散射光的回波来检测生物组织的断层结构，其轴向分辨率可以达到几个微米[3-5]。早期的OCT系统采用时域探测的方式，通过参考臂平面镜的轴向扫描实现对样品深度信息的提取[6]。目前OCT成像通常在傅里叶域进行检测，与时域OCT相比，傅里叶域OCT的灵敏度和成像速度有了显著提高，傅里叶域OCT(Fourier domain OCT，FD-OCT)分为谱域OCT(spectral domain OCT，SD-OCT)和扫频OCT(swept source OCT，SS-OCT)[7-9]。

SD-OCT系统采用光谱仪和线阵相机测量干涉信号的光谱，并通过傅里叶变换重建深度信息。SD-OCT系统中导致灵敏度下降和成像质量恶化的主要原因之一是色散[10]。光的传播速度取决于材料的折射率。当样品臂和参考臂的光纤长度不同时，会发生色散失配，此时系统的点扩散函数(point spread function，PSF)不仅会展宽，而且其峰值强度也会降低[11]。色散补偿是解决样品臂与参考臂色散失配问题的基础。为了解决干涉仪两臂之间色散失配导致的轴向分配率下降的问题，许多基于硬件和软件的色散补偿方法被用于校正样品臂和参考臂之间的色散失配[12-14]。基于硬件的色散补偿方法可以同时对系统色散和样品色散进行矫正，只需要在干涉仪中的一个臂中添加补偿材料，如色散棱镜、光栅、光纤相位调制器等[15-16]。但是这些硬件补偿方法补偿程度较低，并且会提高系统的复杂度和成本。基于软件的色散补偿方法可矫正更高阶的色散，如一种深度依赖的色散补偿方法，基于相位校正信号的迭代调整来优化图像清晰度[17-19]。然而，基于迭代算法的数值补偿方法计算量大，需要更多的计算时间。还可以通过去复共轭镜像和解卷积等方法提高系统成像清晰度等[20-21]。本文提出了一种基于数值多项式拟合分析的方法来解决SD-OCT系统的色散问题，通过消除样品臂和参考臂之间色散失配引起的非线性相位项来实现色散补偿，从而提升成像质量。

2 理论推导

SD-OCT系统的轴向分辨率取决于光源的相干长度，对于高斯型光源，系统的轴向分辨率可以表示为

在谱域光学相干层析成像技术中，光谱仪采集到的干涉信号光谱可以表示为

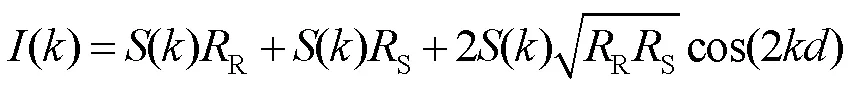
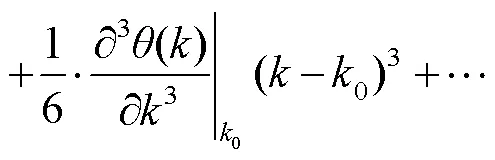
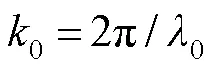
为了得到补偿相位项()，在对波数空间进行线性插值之后，频谱通过傅里叶变换到波长空间，在波长空间移动使得相干函数集中在原点。然后通过傅里叶逆变换得到波数空间的复数谱信号。相位项()等于虚部与实部比值的反正切函数。为了分析不同阶次的拟合效果，对相位进行了二阶、三阶和四阶多项式拟合。为了计算出相位中的高阶色散因子，采用多项式对相位进行拟合，通过最小二乘法计算出多项式的系数。补偿相位项()可以用相位补偿方程表示：

调整系数–2以消除群速度色散不平衡，调整系数–3以消除三阶色散不平衡。经过色散补偿后，利用快速傅里叶的逆变换将干涉信号从空间转换到空间，得到点扩展函数，点扩展函数的半高宽对应于SD-OCT轴向分辨率。

3 实验结果与讨论分析

SD-OCT系统的示意图如图1所示。宽带光源(D-840-HP SM fiber light source，Superlum)是由两块超辐射发光二极管(superluminescent diode，SLD)拼接而成，中心波长为846 nm，带宽为103.6 nm。宽带光源发出的光首先经过光隔离器，目的是防止光沿着光路返回进入光源，对光源造成损伤。光纤耦合器使用中心波长为850 nm，分光比为50: 50的宽带耦合器。光束通过50/50光纤耦合器分别传输到参考臂和样品臂。参考臂由偏振控制(PC)、准直器、透镜和反射镜组成。样品臂由偏振控制(PC)、准直器、二维振镜和透镜组成，其中二维振镜用于实现样品的横向扫描。样品臂和参考臂返回的干涉信号由光谱仪接收。该光谱仪由光纤准直器、中心波长为840 nm的1200 线/mm透射光栅、焦距为150 mm的聚焦透镜和线阵CCD组成。该线阵CCD相机(E2v，EV71YEM2CL2014-BA0)由2048个像素点组成，每个像素点的尺寸为14mm×14mm。CCD相机采用的A扫描频率为5 kHz。最后通过图像采集卡将数据传输到计算机。数据处理由VC++和MATLAB编程实现。

图1 SD-OCT系统示意图

宽带光源的半高宽103.6 nm，中心波长为846 nm。相应的理论轴向分辨率约为3.05 μm。然而，由于光谱的形状不是高斯分布的，因此采用光谱整形的方法来优化图像质量，导致测量的轴向分辨率降低。在样品臂中放置一个反射镜，每隔100mm在～1.5 mm的成像深度内测量点扩散函数。SD-OCT系统灵敏度的下降如图2所示，SD-OCT系统未进行色散补偿时，在零光程差附近色散失配较小，点扩散函数没有明显展宽，轴向分辨率较高。随着光程差增大，色散失配变大，对应的点扩散函数脉宽增加且峰值强度降低，轴向分辨率显著下降。

3.1 相位信息

用2048像素的线阵CCD相机可以采集到干涉信号。在样品臂中放置一个反射镜，并将光程差调整为0.32 mm。色散补偿过程如图3所示，去除自相关项和直流项，干涉光谱如图3(a)所示。通过对干涉谱进行Hilbert变换，利用复数干涉信号的虚部项除以实部项，再通过反正切函数解析干涉信号的相位信息。图3(b)显示了以单个反射镜为样本的波数空间中作为函数的相位项。相移限制在-π～π范围内，解包裹的相位信息如图3(c)所示，解包裹后的相位与真实相位之间相差一个2π整数倍的初相位，这个初相位可以不用考虑，因为两臂间的光程差只与相位曲线的斜率有关，曲线的斜率与两臂间的光程差成正比。如果不进行色散补偿，相位中高阶色散项的存在会使系统点扩散函数发生展宽，降低系统的轴向分辨率。色散补偿需要对相位中的高阶项进行补偿，通过计算出相位中的高阶色散因子来消除高阶项的影响，提升系统的轴向分辨率。

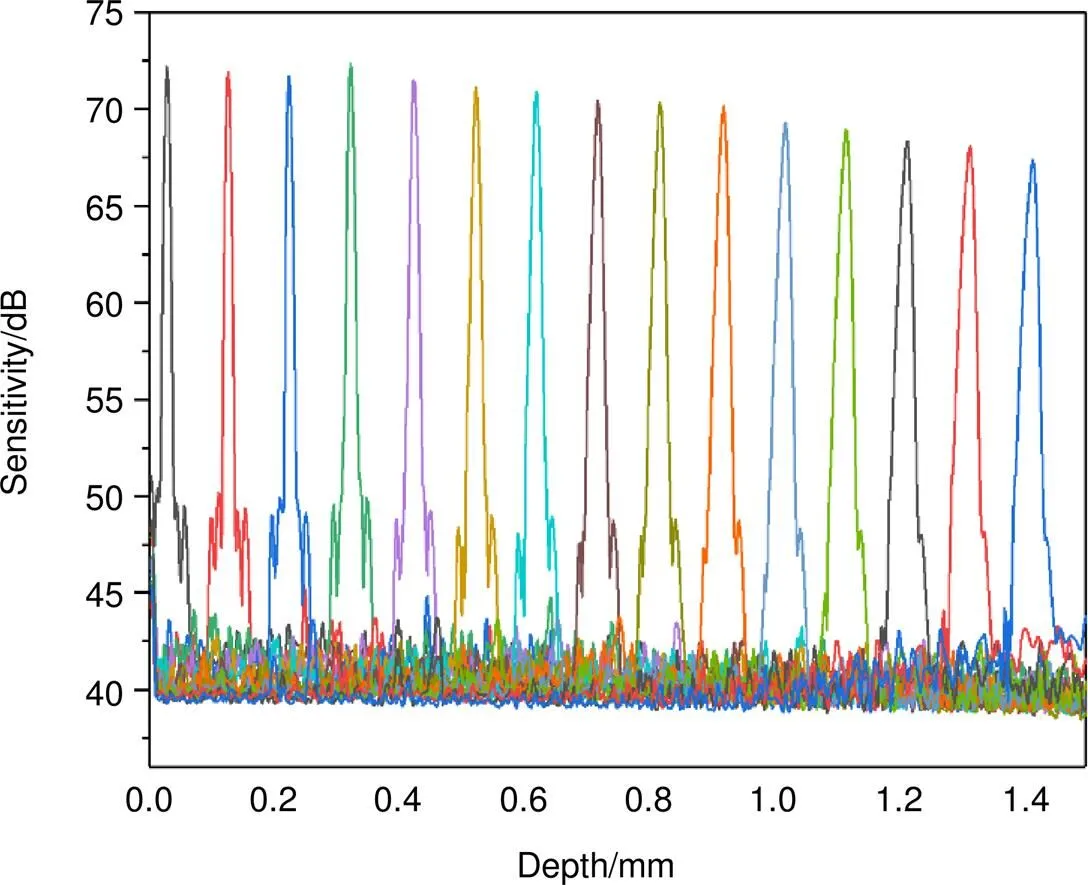
图2 SD-OCT系统未色散补偿的滚降图

图3 测得的干涉信号的强度和相位。(a) 干涉信号；(b) 通过希尔伯特变换解析出的相位；(c) 解包裹后的相位

3.2 色散补偿

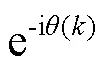
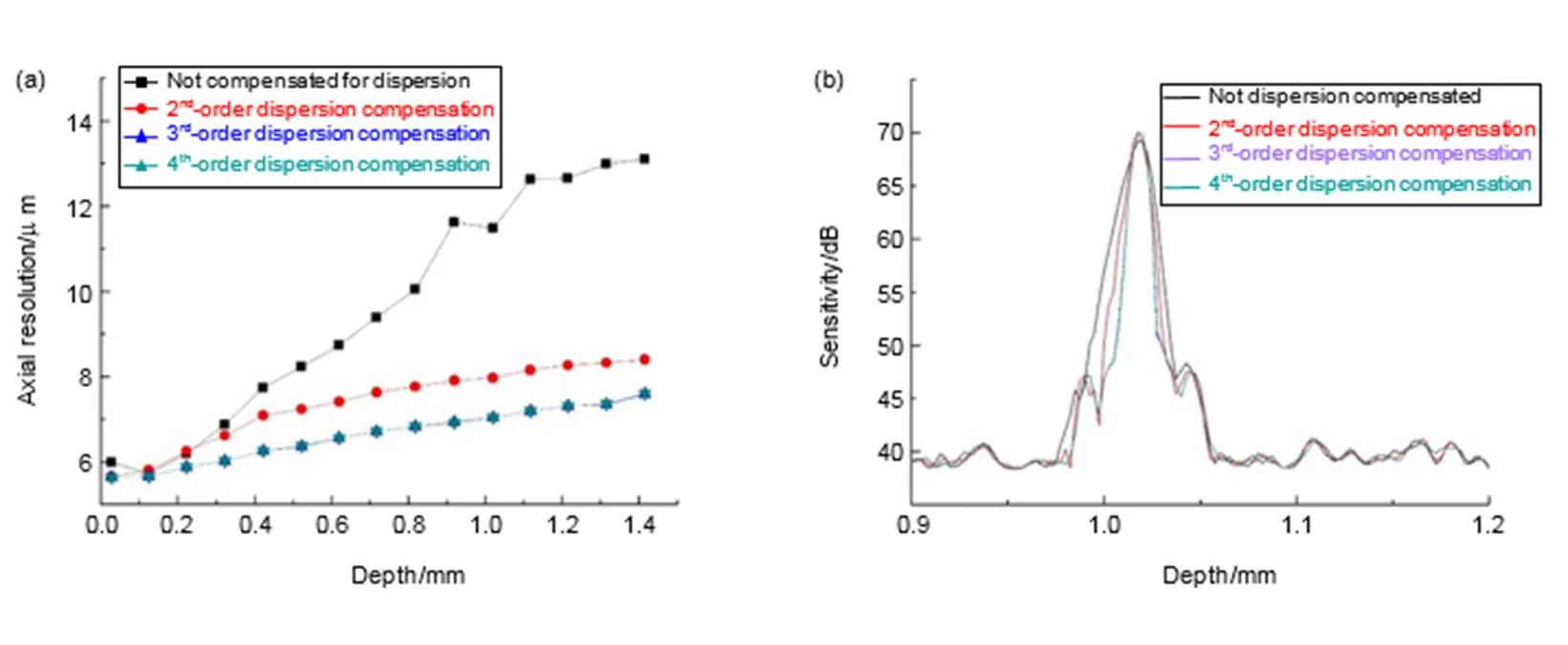
图4 不同色散补偿方案对系统轴向分辨率和PSF的影响。(a) 在0～1.5 mm深度范围的轴向分辨率；(b) 在1.02 mm处的点扩散函数

图5显示了通过三阶数值色散补偿和通过迭代法优化二阶和三阶项之后的点扩散函数的比较。该方法使用迭代过程来测量和优化图像的锐度。图中显示的是成像深度为1.02 mm时的点扩散函数。采用三阶色散补偿方法测得的半高宽约为～7.5 µm，采用数值迭代补偿方法测得的半高宽为～7.0 µm。采用数值迭代补偿方法得到的轴向分辨率略好于采用三阶色散补偿方法得到的轴向分辨率。但采用三阶色散补偿方法的计算量要小得多。

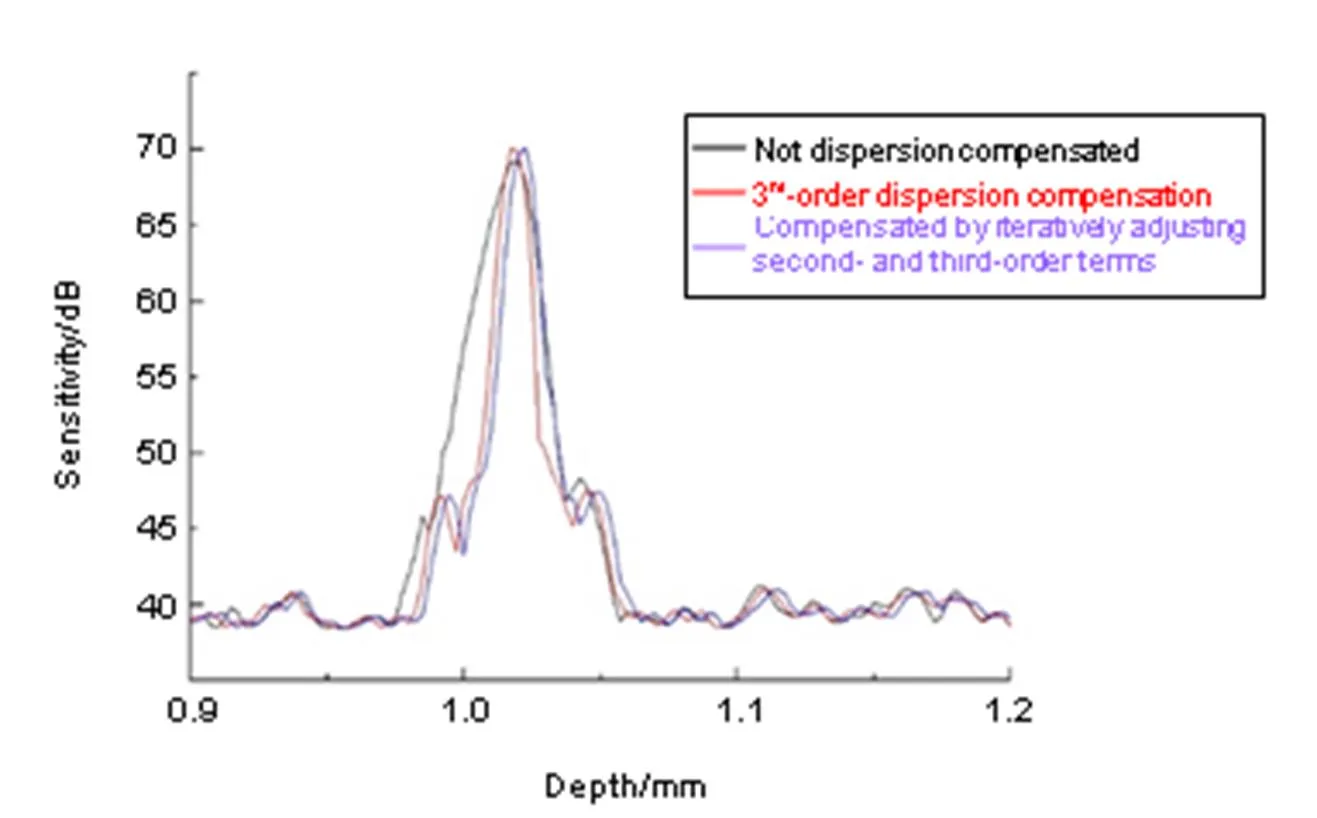
图5 无色散补偿、三阶色散补偿和数值迭代补偿的实测点扩散函数的比较

图6给出了SD-OCT系统经过色散补偿后的滚降(roll-off)图和色散补偿前后点扩散函数的峰值对比图，从图6(a)可以看出，SD-OCT系统进行色散补偿后，随着光程差的增加，点扩散函数的展宽基本保持不变，并且峰值强度同色散补偿前相比也保持较高的水平，轴向分辨率得到很大提升。图6(b)对比了色散补偿前后点扩散函数的峰值。从图中可以看出，经过色散补偿后，点扩散函数的峰值在成像深度为0～0.6 mm范围内差别不大，随着成像深度逐渐增加，色散补偿前后的点扩散函数峰值差值逐渐增大，在深度为1.3 mm处达到最大值1.2 dB，而PSF 的峰值与底部噪声功率的差值可以衡量图像的信噪比，表明色散补偿后信噪比得到有效提升，提升的最大值达到1.2 dB。

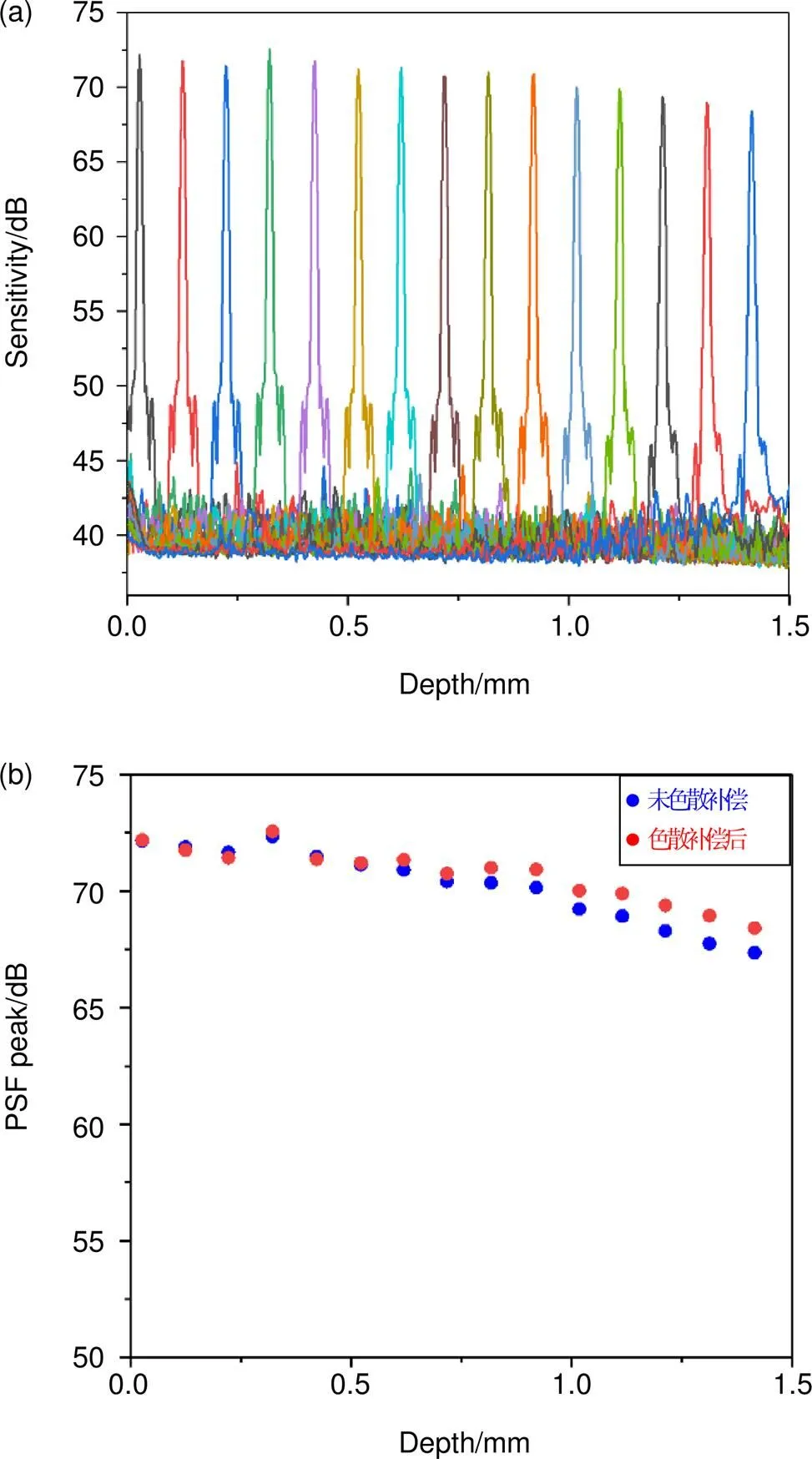
图6 (a) SD-OCT系统色散补偿后的滚降图; (b) 色散补偿前后PSF峰值对比图

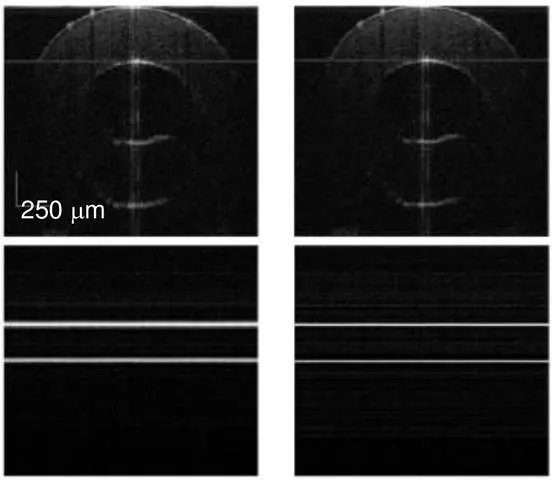
为了验证三阶色散补偿对样品SD-OCT图像的补偿效果，分别对橡胶管和单层盖玻片的图像进行了色散补偿。图7(a)和图7(b)显示了对橡胶管的OCT图像的色散补偿前后的效果，可以看出在成像深度较大的区域，图像清晰度得到了提升。图7(c)和图7(d)显示了色散补偿前后盖玻片样品的OCT图像，将盖玻片上下表面的轴向信息提取出来后，并分别对这两部分进行相位补偿。可以看出对于轴线上样品的展宽信息，色散补偿能够有效提升图像的锐度，成像效果得到明显提升。

图7 橡胶管、盖玻片样品的OCT图像。(a)，(c) 色散补偿前；(b)，(d) 色散补偿后

4 结 论

本文提出了一种基于三阶多项式拟合的色散补偿方法。在SD-OCT系统中，当参考臂和样品臂之间存在色散失配时，干涉信号的相位会出现高阶项，进而展宽系统的点扩散函数，降低系统轴向分辨率。对于任意光程差位置的干涉信号，其相位可以通过泰勒级数展开，色散补偿的目的就是消除相位中的高阶项对系统的影响。干涉信号的相位通过希尔伯特变换提取，提取出的相位经过解包裹后可以还原出相位与波数的关系，接着利用三阶多项式拟合相位，得到的高阶色散因子可用于消除相位中的高阶项。实验使用平面镜样品测量系统在不同光程差位置的点扩散函数，发现光程差越大，系统的点扩散函数展宽越明显。通过比较二阶、三阶和四阶色散补偿三种方案对系统轴向分辨率的影响，发现只需要将干涉信号的相位补偿到三阶项就可以达到较好的补偿效果，最后通过对比色散补偿前后盖玻片和橡胶软管的SD-OCT图像，证明了该方法的有效性和可行性。

[1] Huang D, Swanson E A, Lin C P,. Optical coherence tomography[J]., 1991, 254(5035): 1178–1181.

[2] Fujimoto J G. Optical coherence tomography for ultrahigh resolutionimaging[J]., 2003, 21(11): 1361–1367.

[3] Drexler W, Morgner U, Kärtner F X,.ultrahigh-resolution optical coherence tomography[J]., 1999, 24(17): 1221–1223.

[4] Povazay B, Bizheva K, Unterhuber A,. Submicrometer axial resolution optical coherence tomography[J]., 2002, 27(20): 1800–1802.

[5] Wang Y M, Zhao Y H, Nelson J S,. Ultrahigh-resolution optical coherence tomography by broadband continuum generation from a photonic crystal fiber[J]., 2003, 28(3): 182–184.

[6] Fercher A F, Hitzenberger C K, Kamp G,. Measurement of intraocular distances by backscattering spectral interferometry[J]., 1995, 117(1–2): 43–48.

[7] Leitgeb R, Hitzenberger C K, Fercher A F. Performance of Fourier domain vs. time domain optical coherence tomography[J]., 2003, 11(8): 889–894.

[8] de Boer J F, Cense B, Park B H,. Improved signal-to-noise ratio in spectral-domain compared with time-domain optical coherence tomography[J]., 2003, 28(21): 2067–2069.

[9] Choma M A, Sarunic M V, Yang C,. Sensitivity advantage of swept source and fourier domain optical coherence tomography[J]., 2003, 11(18): 2183–2189.

[10] Hitzenberger C K, Baumgartner A, Drexler W,. Dispersion effects in partial coherence interferometry: implications for intraocular ranging[J]., 1999, 4(1): 144–151.

[11] Jeon M, Kim J, Jung U,. Full-range k-domain linearization in spectral-domain optical coherence tomography[J]., 2011, 50(8): 1158–1163.

[12] Ni G M, Zhang J, Liu L,. Detection and compensation of dispersion mismatch for frequency-domain optical coherence tomography based on A-scan’s spectrogram[J]., 2020, 28(13): 19229–19241.

[13] Iyer S, Coen S, Vanholsbeeck F. Dual-fiber stretcher as a tunable dispersion compensator for an all-fiber optical coherence tomography system[J]., 2009, 34(19): 2903–2905.

[14] Liu D, Ge C B, Xin Y,. Dispersion correction for optical coherence tomography by the stepped detection algorithm in the fractional Fourier domain[J]., 2020, 28(5): 5919–5935.

[15] Attendu X, Ruis R M, Boudoux C,. Simple and robust calibration procedure for-linearization and dispersion compensation in optical coherence tomography[J]., 2019, 24(5): 056001.

[16] Singh K, Sharma G, Tearney G J. Estimation and compensation of dispersion for a high-resolution optical coherence tomography system[J]., 2018, 20(2): 025301.

[17] Marks D L, Oldenburg A L, Reynolds J J,. Autofocus algorithm for dispersion correction in optical coherence tomography[J]., 2003, 42(16): 3038–3046.

[18] Yasuno Y, Hong Y, Makita S,.high-contrast imaging of deep posterior eye by 1-μm swept source optical coherence tomography and scattering optical coherence angiography[J]., 2007, 15(10): 6121–6139.

[19] Pan L H, Wang X Z, Li Z L,. Depth-dependent dispersion compensation for full-depth OCT image[J]., 2017, 25(9): 10345–10354.

[20] Liu X Y, Ke M Y, Yao X W,. Stable complex conjugate artifact removal in OCT using circularly polarized light as reference[J]., 2020, 45(14): 3977–3980.

[21] Wang K, Ding Z H, Chen M H,. Deconvolution with fall-off compensated axial point spread function in spectral domain optical coherence tomography[J]., 2011, 284(12): 3173–3180.

Research on dispersion compensation technology for SD-OCT system

Jiang Panqiu, Wang Pinghe*

State Key Laboratory of Electronic Thin Films and Integrated Devices, School of Optoelectronic Science andEngineering, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China

SD-OCT images of rubber hose and coverslip. (a), (b) Not compensated for dispersion; (c), (d) 3rd-order dispersion compensation

Overview:Optical coherence tomography (OCT) is an optical imaging modality that enables high-resolution, cross-sectional, and three-dimensional volumetric imaging of the internal microstructure in biological tissues and materials. SD-OCT system has a broadband source and a spectrometer with a line scan camera. One of the main problems of the SD-OCT system is that chromatic dispersion causes the decrease of sensitivity and imaging quality. Many different methods have been proposed, including hardware-based and software-based methods. Solutions include physically matching the dispersion in both arms by adding compensating materials, gratings, or fiber-stretchers in one of the interferometer arms. However, all these methods only compensate up to second-order dispersion and have the same pitfalls of complexity and cost. Various software-based methods have also been proposed to solve the problem of dispersion mismatch. Some rely on an iterative adjustment of a phase correction signal to optimize image sharpness.

We propose a dispersion compensation method based on the numerical polynomial fitting analysis in the spectral domain optical coherence tomography. This method obtains the dispersion factor by fitting the phase of the interference signal and removes the dispersion mismatch terms, which can significantly improve the system axial resolution compared with non-dispersion compensation.

To illustrate that the numerical dispersion compensation method has an optimized effect on the axial resolution of the SD-OCT system, we measured the axial resolution at different depths and compared the PSF of 2nd-order, 3rd-order, and 4th-order dispersion compensation. The results prove that the axial resolution obtained by 3rd-order dispersion compensation is in good agreement with it measured by 4th-order dispersion compensation, and is better than it measured by non-dispersion compensation and 2nd-order dispersion compensation. The third-order dispersion compensation has a visible optimization effect.

A comparison between the measured PSF by third-order numerical dispersion compensation and by the iterative dispersion compensation technique was carried out. The PSF is measured at the imaging depth of 1.02 mm. The measured FWHM with third-order dispersion compensation is ～7.5 µm and that with the iterative dispersion compensation technique is ～7.0 µm. The iterative dispersion compensation yields a little better resolution than the three-order dispersion compensation. However, it requires more computation.

The images of rubber hose and coverslip in the experiment are shown in the Figure. Using the method of the third-order dispersion compensation, two-dimensional imaging of rubber hose and coverslip are shown in Figure (c) and Figure (d), respectively. In order to contrast the effect of this method, the diagrams without dispersion compensation are shown in Figure (a) and Figure (b). The diagram with third-order dispersion compensation has a good sharpness in the deep position.

Jiang P Q, Wang P HResearch on dispersion compensation technology for SD-OCT system[J]., 2021, 48(10): 210184; DOI:10.12086/oee.2021.210184

Research on dispersion compensation technology for SD-OCT system

Jiang Panqiu, Wang Pinghe*

State Key Laboratory of Electronic Thin Films and Integrated Devices, School of Optoelectronic Science andEngineering, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China

Dispersion compensation for the data processing of the spectral domain optical coherence tomography (SD-OCT) system is an important way to improve the imaging quality of the system. A dispersion compensation method for spectral domain optical coherence tomography based on numerical polynomial fitting analysis is proposed in this paper. This method obtains the dispersion factor by fitting the phase of the interference signal and removes the dispersion mismatch terms, which can significantly improve the system axial resolution compared with non-dispersion compensation. The SD-OCT system is used to measure the axial resolution and signal-to-noise ratio (SNR) at different positions of the optical path difference, and the effectiveness and reliability of the method are verified by analyzing the axial resolution and the SNR of the system before and after the dispersion compensation technology. Finally, we found that the third-order dispersion compensation has a visible optimization effect within the imaging depth of ～1.5 mm.

SD-OCT; dispersion compensation; polynomial fitting; resolution; imaging quality

National Key R&D Program of China (2016YFF0102003, 2016YFF0102000)

10.12086/oee.2021.210184

O439

A

* E-mail: wphsci@uestc.edu.cn

姜盼秋，汪平河. 谱域光学相干层析系统的色散补偿技术研究[J]. 光电工程，2021，48(10): 210184

Jiang P Q, Wang P H. Research on dispersion compensation technology for SD-OCT system[J]. Opto-Electron Eng, 2021, 48(10): 210184

2021-06-02；

2021-10-13

国家重点研发计划项目(2016YFF0102003，2016YFF0102000)

姜盼秋(1989-)，女，硕士，讲师，主要从事光学相干层析成像技术的研究。E-mail：jiangpanqiu_1006@sina.com

汪平河(1976-)，男，博士，教授，主要从事光学相干层析成像技术和光纤激光器的研究。E-mail：wphsci@uestc.edu.cn

版权所有©2021中国科学院光电技术研究所