基于运动估计的波前畸变预测方法研究

周 鑫，李新阳

基于运动估计的波前畸变预测方法研究

周 鑫1,2，李新阳1*

1中国科学院光电技术研究所自适应光学重点实验室，四川 成都 610209；2中国科学院大学，北京 100049

实际自适应光学控制系统中存在的时间延迟，导致校正器生成的校正面形与实际的波前畸变不匹配，产生校正滞后误差。基于大气冻结湍流假设，提出了一种基于运动估计的波前畸变预测方法，来补偿时间延迟带来的影响。方法具体采用模板匹配算法，根据参考帧和当前帧的波前复原图像进行大气湍流运动方向估计，然后对当前帧进行移动处理来实现对下一帧图像的预测。通过采用不同采样频率、不同横向风速度的仿真数据对比，评估预测方法的适用范围，讨论回溯帧数对预测效果的影响。也与采用最小递归二乘(RLS)模式预测方法的预测效果进行比较。仿真结果显示，在波前复原图像变化趋势较为明显的情况下，即横向风对大气湍流变化影响占主导地位时，方法表现更好，使得在天气较为恶劣的情况下仍能保持更佳的预测效果。最后使用实际天狼星观测数据对预测方法进行验证，整体仍保持预测效果。

自适应光学；湍流预测；运动估计；波前校正

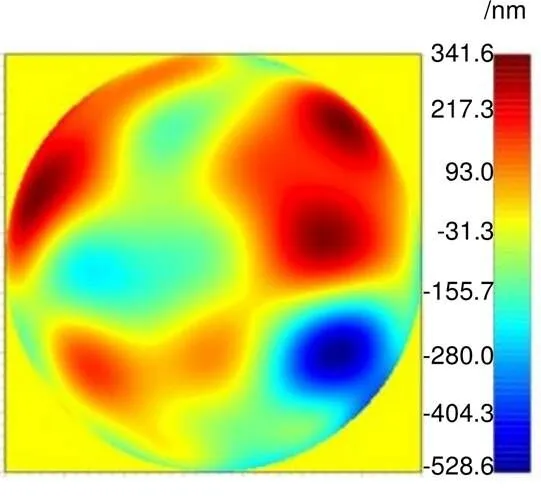
1 引 言

自适应光学(Adaptive optics，AO)系统以实时检测、控制、校正的方式来减少时间、空间上随机变化的波前像差，抑制大气湍流对光学系统成像质量的影响[1-2]。实际AO控制系统完成图像采集、整体斜率计算、波前复原运算和控制运算等信号处理和控制任务，产生系统采样周期2～3倍的时间延迟[2]。而系统时间延迟导致校正器生成的校正面形与实际的波前畸变不匹配，产生校正滞后误差[3]。时间延迟越长，系统的整体控制性能越差[4-5]，对观测目标波前畸变进行预测可以补偿这一影响。

目前预测方法中，迭代预测方法对系统误差最小化，如递归最小二乘(least recursive squares，RLS)控制算法，计算过程简单，不容易陷入局部最小点，但当像差的模式阶数较高时无法在短时间内收敛[6-7]。基于模型预测方法使用大气湍流模型预测波前像差的变化，如线性二次高斯(LQG)控制算法，近似效果较好，但模型的精准度与控制器的控制难易度相矛盾[8-9]。神经网络预测方法采用神经网络结构对历史数据进行端到端预测，如前馈神经网络对波前斜率数据，较为显著地提高误差校正精度，但训练数据需求量大，较难训练出对大气湍流变化泛化能力较好的结构[10-11]。

在大气冻结湍流假设下，一定时间尺度内大气湍流的空间特性不会发生显著性的变化，大气湍流在大气横向风的驱动下运动[12]。因此可以直接利用横向风速信息对当前和历史的波前像差进行线性预测，得到未来的波前像差，该预测方法的计算精度取决于横向风参数的估计准确度。Johnson等[13]使用高斯¾牛顿算法对横向风参数进行迭代求解，李正汉[14]采用运动估计的方法计算横向风向和风速，线性预测后均能提高系统性能。故本文采用模板匹配算法对横向风参数进行运动估计，实现对波前畸变变化情况的预测，补偿时间延迟带来的影响。

2 预测方法原理

2.1 大气湍流理论

目前，自适应光学领域相关研究基本建立在Kolmogorov湍流统计理论[15]之上，即在惯性区域折射率结构函数满足“三分之二定律”，为

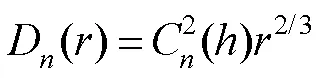
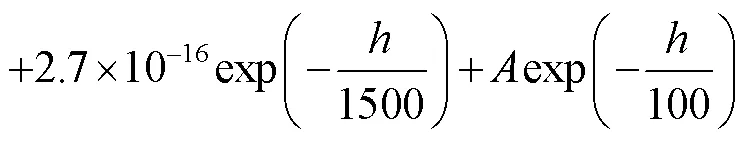
而大气中风速随海拔高度的变化也存在模型表述，常用Buffton风速模型，为

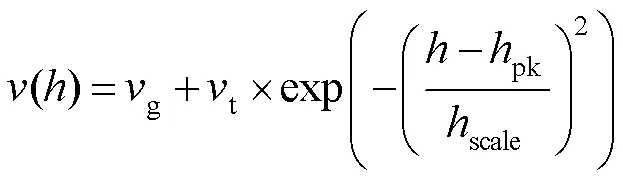
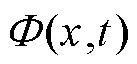
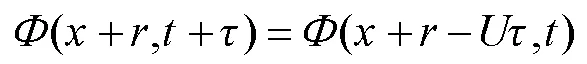
其中：为流向平均速度[16]。即未来一段时间的大气湍流信息可以通过现在和历史的大气湍流移动一段距离后得到，湍流保持不变的时间尺度大约在1 ms～10 ms范围内[17]。故本文通过以上大气湍流理论产生波前畸变仿真数据，实现对目标光复原波前变化情况的分析。

2.2 模板匹配运动估计算法

模板匹配算法是将图像分成许多互不重叠的块，并假定块内所有像素的运动速度和运动方向都相同，然后根据匹配准则在参考图像的某一给定特定搜索范围内找出与当前块最相似的块，匹配块与当前块之间代价函数最小的运动轨迹即为运动矢量[18]。为了提高估计的精度和计算效率，本文选用自适应十字模式搜索(ARPS)算法的搜索策略和匹配准则。ARPS算法的匹配准则选用计算最为简便的平均绝对误差(MAD，用MAD表示)作为代价函数，计算公式为

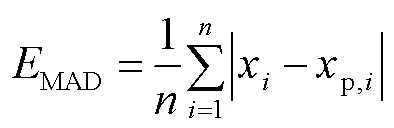
因为图像整体的运动趋势是固定的，则相邻的匹配块所估计出的运动参数是相近的。ARPS算法每次匹配的搜索策略便是在第一步搜索时，使用已估计的运动参数作为初始搜索间隔找到大致的匹配方向，然后使用小模板对周边区域进行精准匹配，减少收敛到最小误差位置的计算次数[19]。由于ARPS算法存在陷入局部最小点的可能性，因此最终图像整体的运动参数选取各有效匹配区域MAD较小的几个值进行加权平均。

除冻结湍流的主体影响外，AO系统所接受到的光波前畸变还受到系统内部静态像差、大气温度、湿度扰动等其他因素影响，再加上探测过程产生的噪声误差，导致实际检测到的波前畸变变化偏离冻结湍流假设，因此需要对数据进一步处理。针对这一问题，提出了以下两种改进方法：

1) 对预测后的理想校正残差进行统计，作为先验知识预处理波前畸变数据，以此进行更加准确的运动估计，最终的预测结果也需要加上残差。

2) 直接采用理想校正残差进行预测，参考帧和当前帧相减后会滤去部分短时间内变化不大的成分，保留部分理论仍符合冻结湍流假设。

综上，本文采用模板匹配的运动估计算法进行波前畸变预测，具体根据参考帧和当前帧的波前复原图像进行大气湍流运动方向估计，然后对当前帧进行移动处理来实现对下一帧图像的预测。

2.3 预测效果评价指标

算法的预测效果采用均方根误差(RMS)(RMS)进行评价，未校正图像的RMS(RMS-orig)、未经过预测估计算法的理想校正残差RMS(RMS-del)、经过预测算法的理想校正残差RMS(RMS-pre)依次为

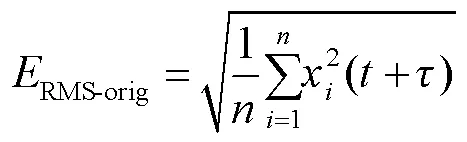
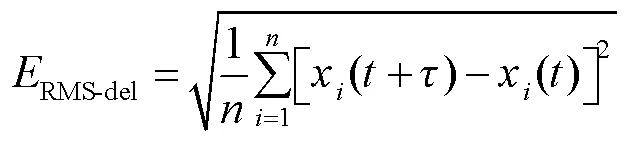
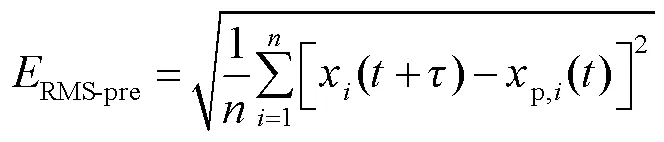
不同算法对实际波前畸变的理想校正效果为

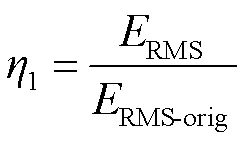
预测算法的提升效果为

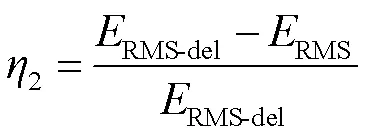
3 仿真结果与讨论

3.1 仿真条件

仿真基于后续实验设置参数，采用Kolmogorov湍流统计理论、HV-57折射率结构常数模型、Buffton风速模型、大气冻结湍流假设，经过傅里叶级数(FS)方法时间演化产生10个大气相位屏。平台海拔高度3150 m，目标海拔高度30 km，目标仰角32.9672°，相位屏均匀分布且位于每段中间位置，各相位屏参数设置如表1所示。

目标波长550 nm，望远镜口径1.8 m，65阶复原波前分辨率465×465，采样频率500 Hz，共采样500帧，前8帧波前复原相位仿真数据如图1所示。

3.2 预测结果

由于65阶复原波前分辨率为465×465，可以将参考帧图像分为5×5个匹配块，每个匹配块为93×93个像素，搜索范围设为运动参数、分量中较大值的两倍。图像边角部分匹配块的空白区域过大，直接抛弃不纳入后续计算。本文通过比较未进行预测估计的(deletion)、直接模板匹配运动预测估计的(prediction)、改进方法1的(improvement 1)、改进方法2的(improvement 2)理想校正残差RMS，对模板匹配运动估计算法及其改进算法的预测效果进行对比。

不同算法的理想校正残差RMS对比如图2(a)所示，其中平均理想校正残差RMS依次为0.0614、0.0508、0.0343、0.0242。结果表明，模板匹配运动估计算法及其改进算法均可以在一定程度上提高预测的准确性。

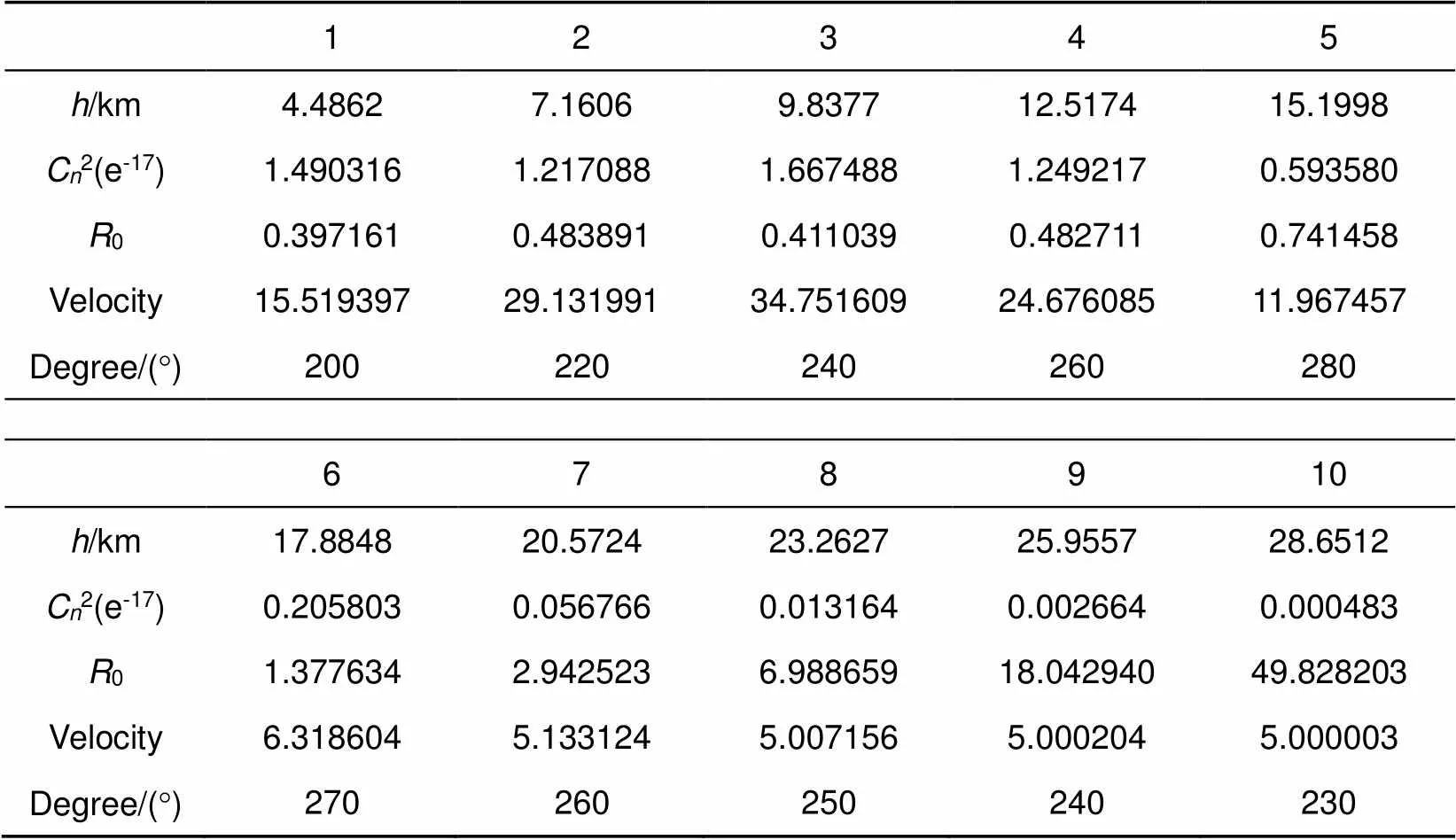
表1 仿真各相位屏参数设置

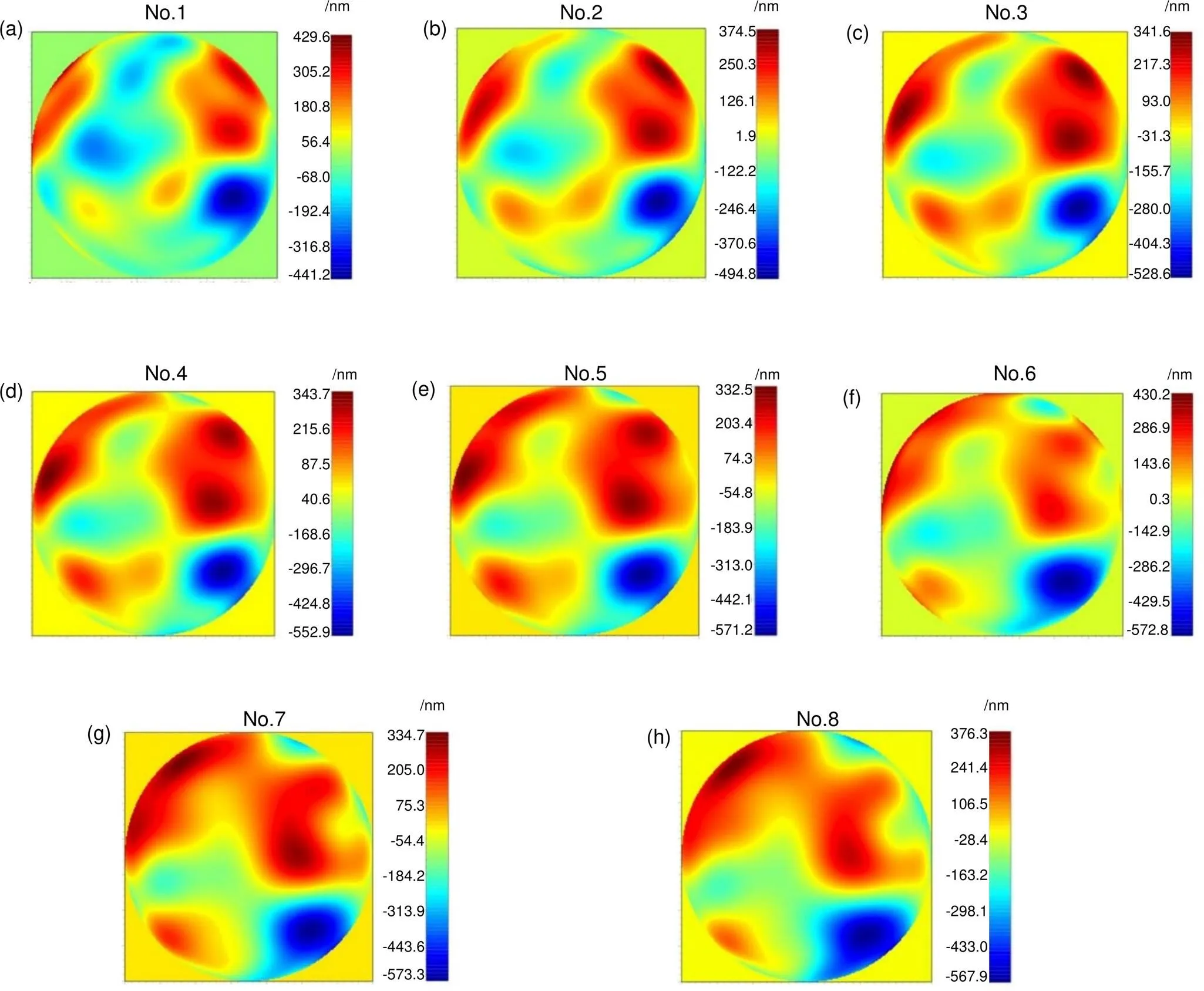
图1 前8帧波前复原相位仿真数据

不同算法对实际波前畸变的理想校正效果如图2(b)所示，其中平均理想校正效果依次为9.54%、7.76%、5.35%、3.76%。结果表明，第一种改进方法在一开始的理想校正效果较差，这是因为算法需要一定的时间去统计先验知识。

预测算法提升效果的概率密度函数如图2(c)所示，其中平均提升效果依次为17.05%、43.97%、60.64%。结果表明，第二种改进方法虽然平均提升效果较好，但分布幅度较窄。相较而言，第一种改进方法分布幅度较宽，比较稳定。

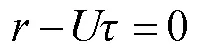
结果表明，在5帧到6帧，即10 ms到12 ms左右算法的预测性能会出现一定程度的下降，但仍具有预测效果，这与大气冻结湍流假设的湍流保持不变时间尺度相匹配。

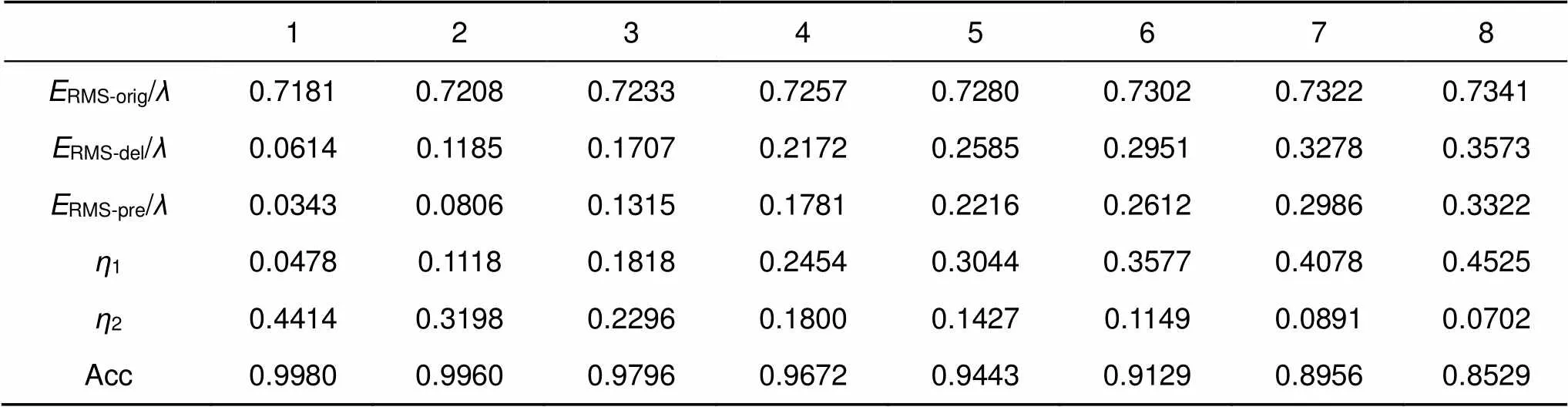
表2 不同风速下算法预测效果对比

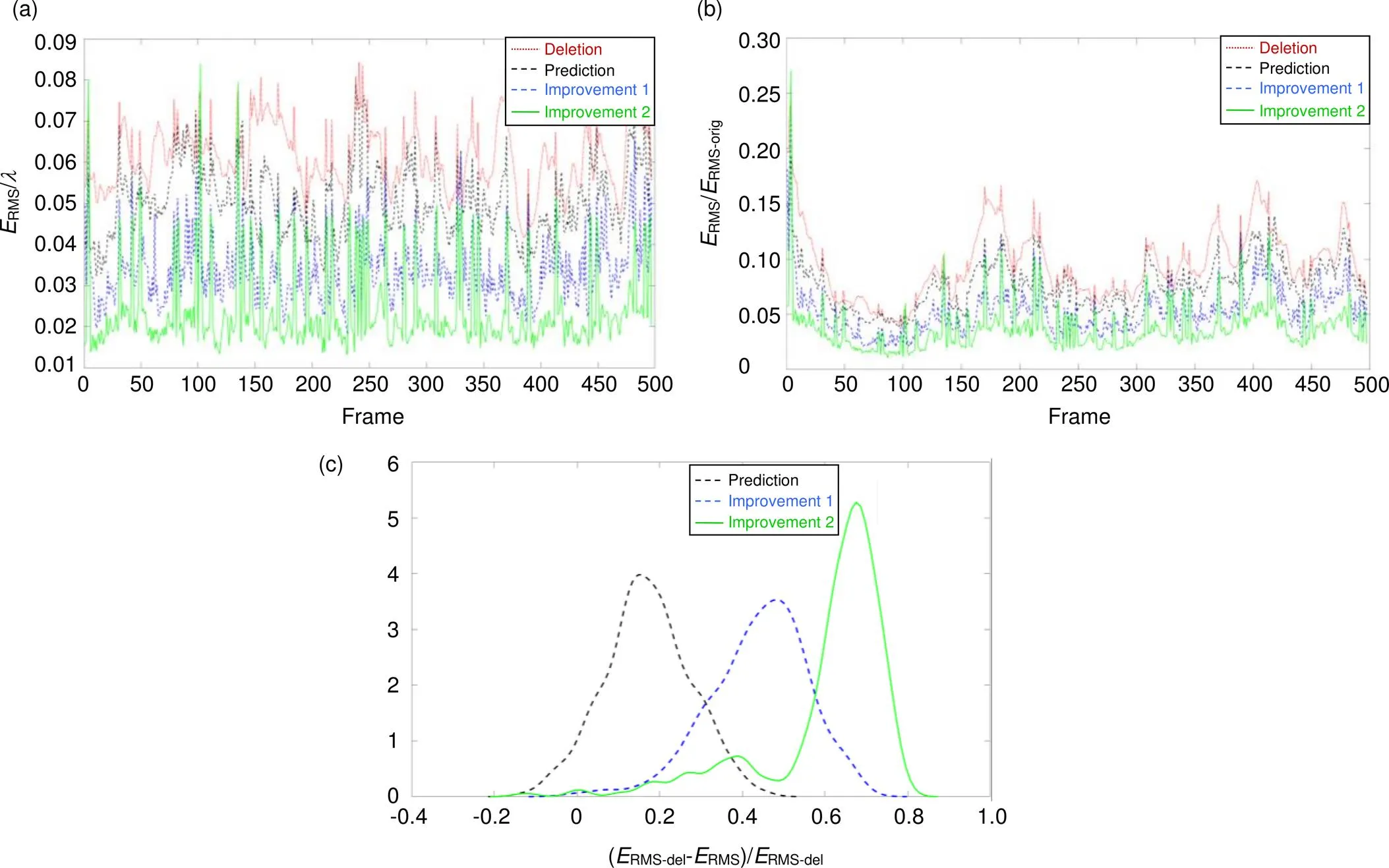
图2 不同算法预测效果对比

3.3 与RLS方法对比

RLS模式预测方法通过最小化每个Zernike模式的平均均方误差进行预测。具体是在每次迭代过程中，根据预测系数和当前与历史Zernike模式来估计未来帧的Zernike模式，在计算平均均方误差时可以加入遗忘因子，使其对近期数据更加敏感[7]。

这仍采用第一种改进方法与RLS模式预测方法对不同风速下的理想校正效果进行对比，RLS模式预测方法对前65个Zernike模式进行预测并复原，回溯帧数3帧，具体结果如图3所示。结果显示，模板匹配运动估计算法理想校正效果较好，随着风速的增大，RLS模式预测方法逐渐失效，无预测效果。这是大风速影响下Zernike模式变化起伏过大导致，算法无法找到变化规律。

4 实验结果与讨论

4.1 实验条件

实验使用云南丽江天文观测站1.8 m望远镜对天狼星进行观测，平台海拔为3193 m，观测条件如表3所示。

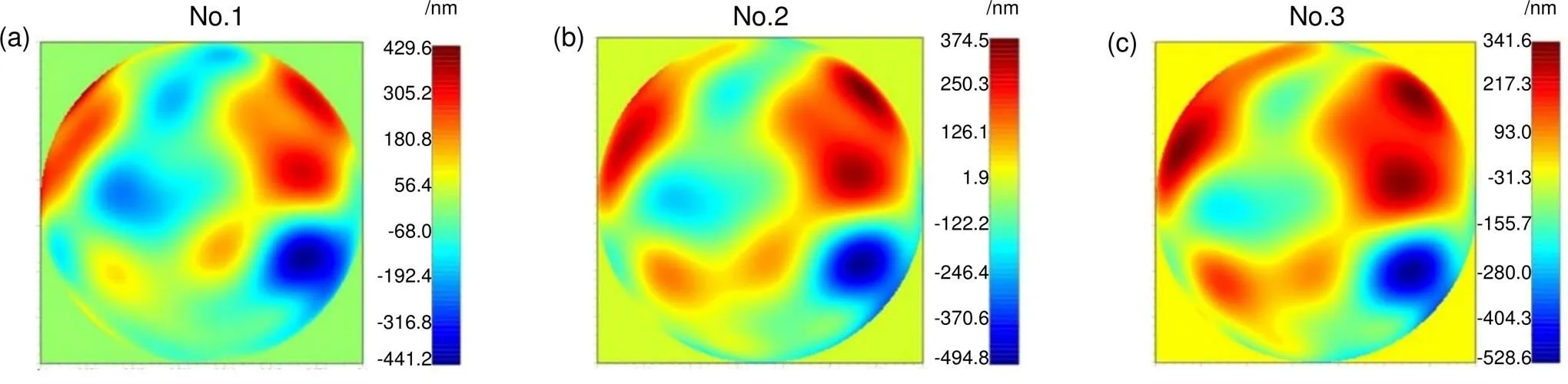
哈特曼传感器图像采集使用法国First Light公司EMCCD相机，型号OCAM2K，靶面240×240，探测有效子孔径数量156个，子孔径分辨率16×16。实验采样频率500 Hz，一次采样2018帧，前4帧哈特曼传感器探测到的光斑阵列如图4所示。

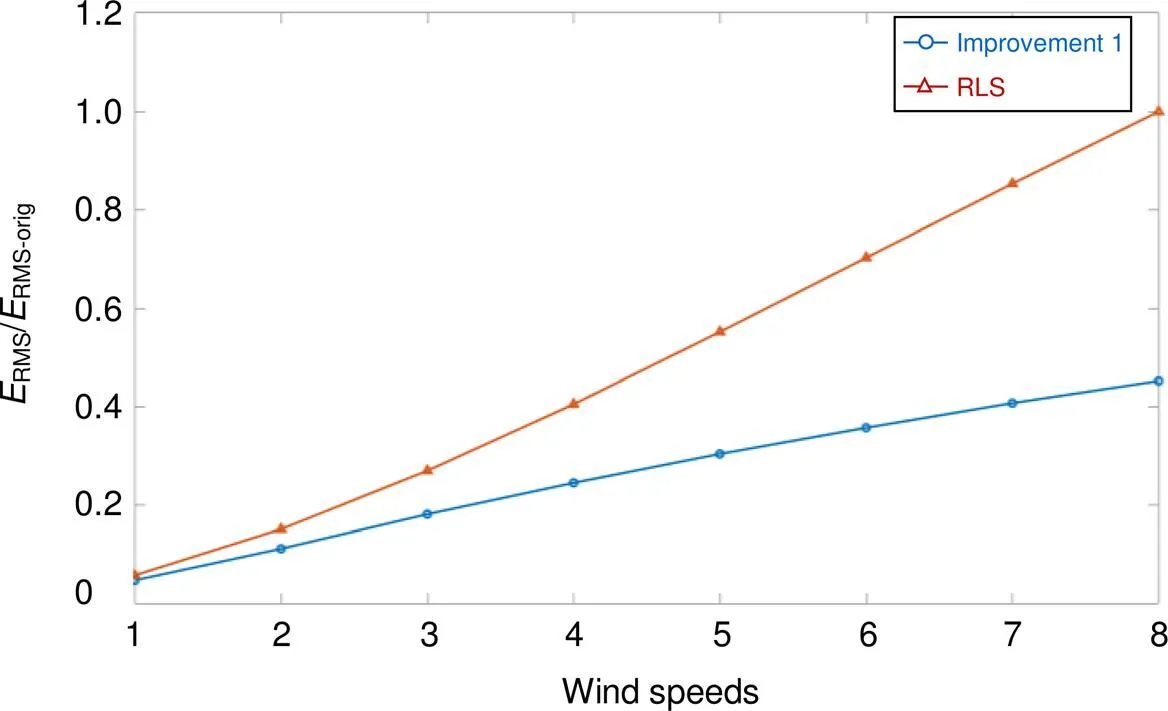
图3 不同风速下运动估计预测与RLS模式预测效果对比

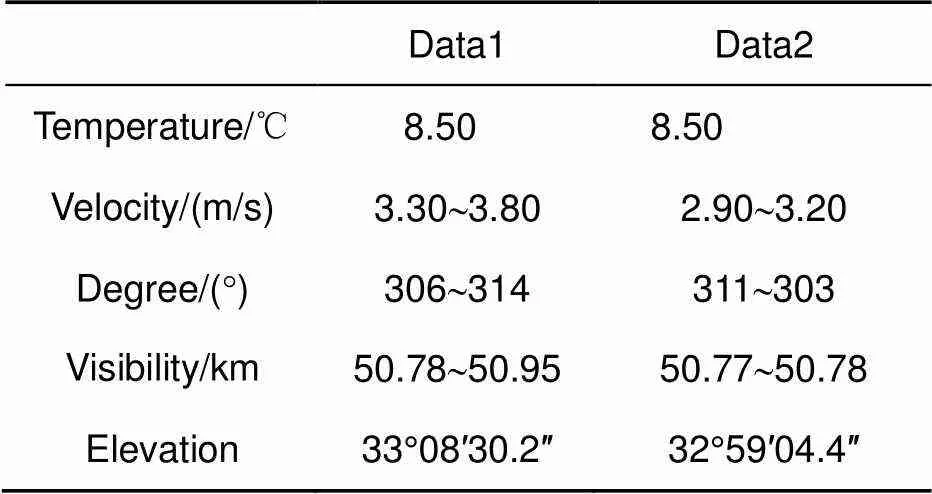
表3 自然星观测条件

4.2 实验结果

由于每隔2帧(6 ms)的参考帧和当前帧波前复原图之间的运动趋势明显且连续性较好，以此对采用第一、二种改进的预测方法进行实验验证，复原波前分辨率为200×200，65阶。

不同算法的前500帧理想校正残差RMS对比如图5(a)所示，其中平均理想校正残差RMS依次为0.8594、0.6778、0.5004。不同算法对实际波前畸变的前500帧理想校正效果如图5(b)所示，其中平均理想校正效果依次为22.88%、17.61%、12.21%。预测算法提升效果的概率密度函数如图5(c)所示，其中平均提升效果依次为15.97%、24.25%。

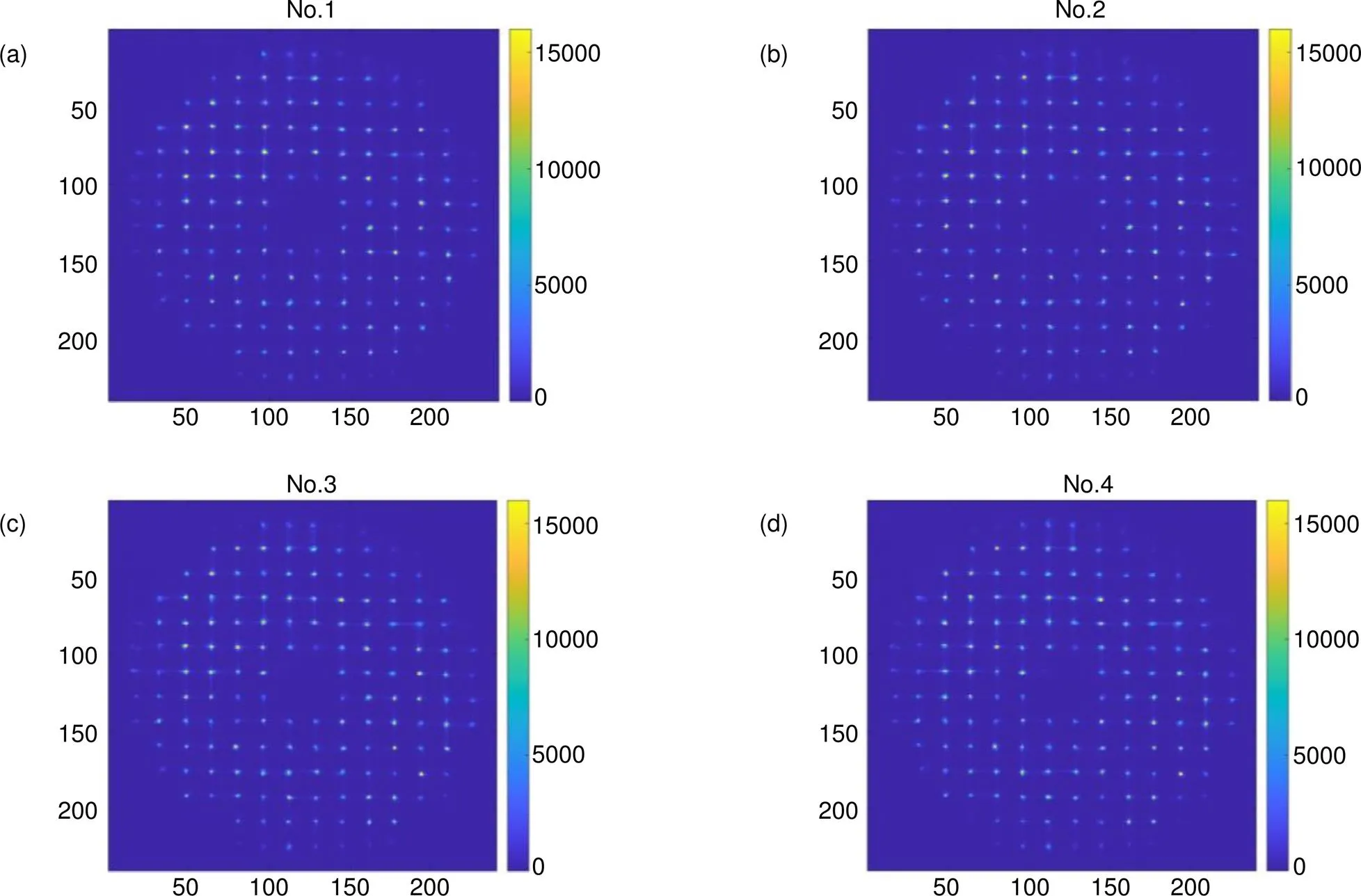
图4 前4帧哈特曼传感器探测图像

实验验证结果表明，模板匹配运动估计算法可以在一定程度上提高预测的准确性，具有一定的实用价值。但无论是第一种还是第二种改进方法都存在严重的反向预测情况，其预测校正后的残差RMS远大于未预测校正残差RMS，但始终小于未校正图像的RMS，这是实际AO控制系统中可以容忍的。

不同的复原面积也会对算法的预测效果产生影响。这也采用第一种改进方法对不同复原条件下的理想校正残差RMS进行计算，具体结果如表4所示。结果显示，增大复原面积可以略微提升预测效果，但与复原运算计算量投入不成正比。

4.3 与RLS方法对比

采用第一种改进方法与RLS模式预测方法对不同风速下的理想校正效果进行对比，RLS模式预测方法对前65个Zernike模式进行预测，并复原计算理想校正残差RMS，回溯帧数3帧，具体结果如图6所示。结果与仿真情况相似，模板匹配运动估计算法在波前畸变图像变化较为明显时预测效果较好，在不明显时两者预测效果相差不大。

5 结 论

本文预测方法采用模板匹配算法对大气湍流运动方向进行估计，并针对理想校正残差做了一定的优化处理，方法计算过程简单，复杂度较低。仿真与实验结果显示，在波前畸变图像变化趋势较为明显的情况下，即横向风对大气湍流变化影响占主导地位时，方法表现更好，使得在天气较为恶劣的情况下仍能保持更佳的预测效果。

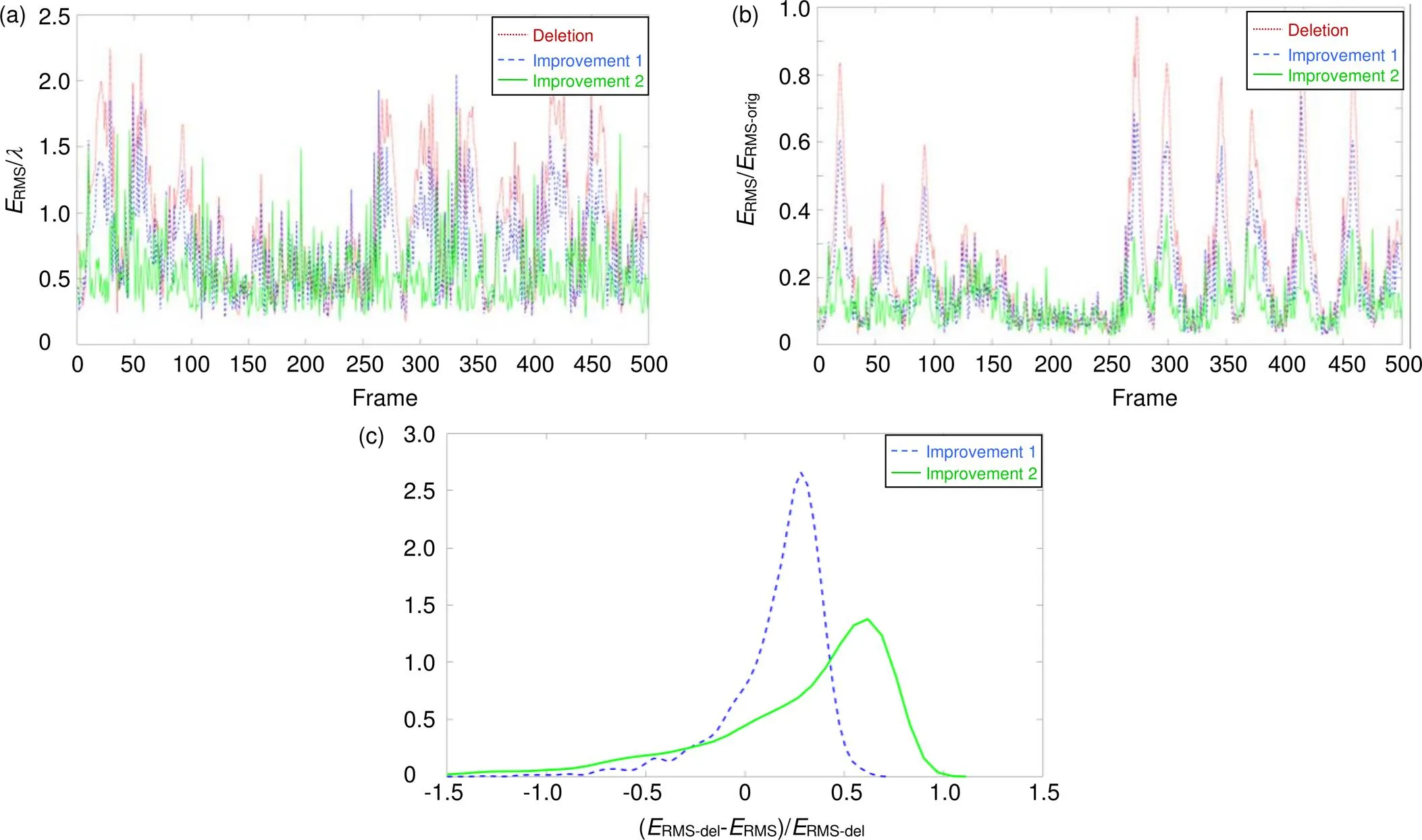
图5 不同算法预测效果对比

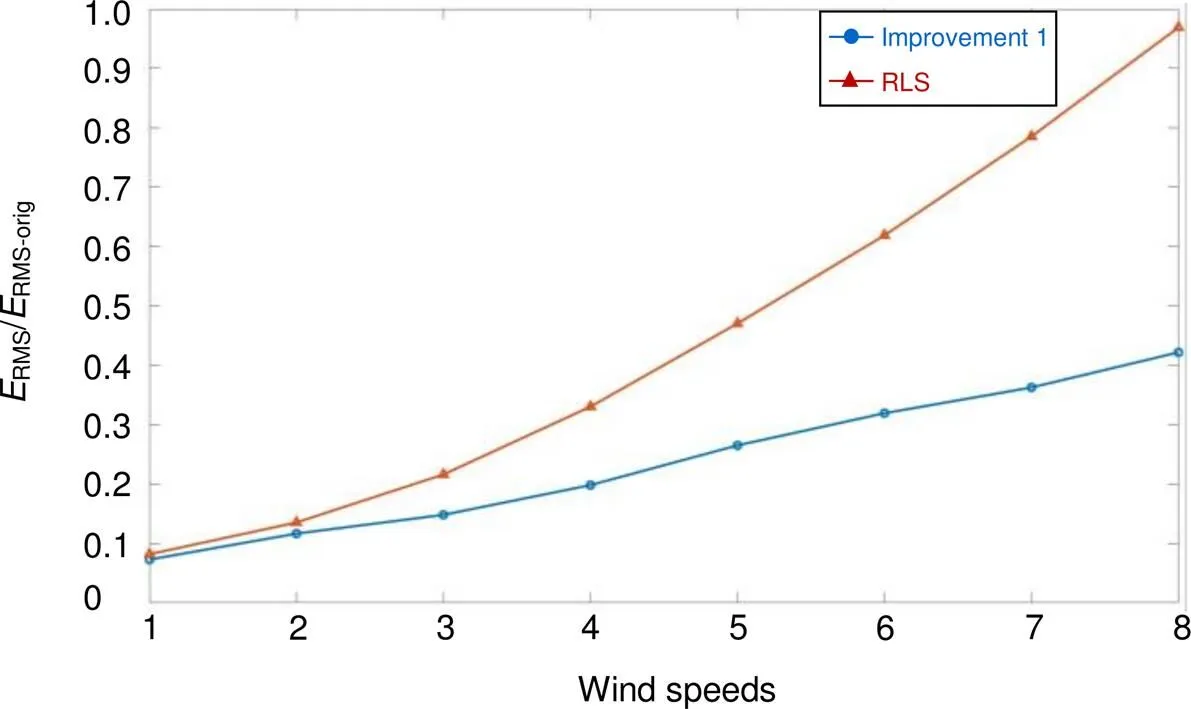
图6 不同风速下运动估计预测与RLS模式预测效果对比

表4 不同复原条件下算法预测效果对比

但算法对不同大气条件的适应性较差，具体取决于实际检测到的波前畸变变化与冻结湍流假设的匹配程度。因此，还需采取方案从波前畸变图像分离出大气冻结湍流成分，或者减少探测过程的噪声影响，进一步提高方法预测准确度和鲁棒性。

[1] Gavel D T. Adaptive optics control strategies for extremely large telescopes[J]., 2002, 4494: 215–220.

[2] Jiang W H. Overview of adaptive optics development[J]., 2018, 45(3): 170489. 姜文汉. 自适应光学发展综述[J]. 光电工程, 2018, 45(3): 170489.

[3] Andersen D R, Fischer M, Conan R,. VOLT: the victoria open loop testbed[J]., 2008, 7015: 70150H.

[4] Li X Y, Jiang W H. Effective bandwidth analysis of adaptive optics control system[J]., 1997, 17(12): 1697–1702.李新阳, 姜文汉. 自适应光学控制系统的有效带宽分析[J]. 光学学报, 1997, 17(12): 1697–1702.

[5] Li X Y, Jiang W H. Analysis of the residual servo variance for an adaptive optics system[J]., 2000, 20(10): 1328–1334. 李新阳, 姜文汉. 自适应光学系统的控制残余方差分析[J]. 光学学报, 2000, 20(10): 1328–1334.

[6] Yan Z J, Li X Y, Rao C H. Numerical simulation of a prediction control algorithm for close-loop adaptive optical system[J]., 2011, 31(1): 0101003. 颜召军, 李新阳, 饶长辉. 一种自适应光学闭环系统预测控制算法的仿真研究[J]. 光学学报, 2011, 31(1): 0101003.

[7] Liu C, Hu L F, Mu Q Q,. Modal prediction for open-loop liquid-crysta adaptive optics systems[J]., 2012, 61(12): 129501. 刘超, 胡立发, 穆全全, 等. 用于开环液晶自适应光学系统的模式预测技术研究[J]. 物理学报, 2012, 61(12): 129501.

[8] Kulcsár C, Raynaud H F, Petit C,. Minimum variance prediction and control for adaptive optics[J]., 2012, 48(9): 1939–1954.

[9] Poyneer L, Véran J P. Predictive wavefront control for adaptive optics with arbitrary control loop delays[J]., 2008, 25(7): 1486–1496.

[10] Paine S W, Fienup J R. Machine learning for improved image-based wavefront sensing[J]., 2018, 43(6): 1235–1238.

[11] Guo H Y, Xu Y J, Li Q,. Improved Machine Learning Approach for Wavefront Sensing[J]., 2019, 19(16): 3533.

[12] Taylor G I. The spectrum of turbulence[J]., 1938, 164(919): 476–490.

[13] Johnson L C, Gavel D T, Wiberg D M. Bulk wind estimation and prediction for adaptive optics control systems[J]., 2011, 28(8): 1566–1577.

[14] Li Z H. Predictive compensation and image registration in adaptive optics systems based on motion estimation[D]. Chengdu: University of Chinese Academy of Sciences (Institute of Optics and Electronics, Chinese Academy of Sciences), 2020.李正汉. 基于运动估计的自适应光学系统预测校正与图像配准技术研究[D]. 成都: 中国科学院大学(中国科学院光电技术研究所), 2020.

[15] Kolmogorov A N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers[J]., 1991, 434(1890): 9–13.

[16] He G W, Jin G D, Yang Y. Space-time correlations and dynamic coupling in turbulent flows[J]., 2017, 49(1): 51–70.

[17] Schock M, Spillar E J. Method for a quantitative investigation of the frozen flow hypothesis[J]., 2000, 17(9): 1650–1658.

[18] Zhu C, Lin X, Chau L P. Hexagon-based search pattern for fast block motion estimation[J]., 2002, 12(5): 349–355.

[19] Biswas B, Mukherjee R, Chakrabarti I,. A high-speed VLSI architecture for motion estimation using modified adaptive rood pattern search algorithm[J]., 2018, 37(10): 4548–4567.

Wavefront distortion prediction method based on motion estimation

Zhou Xin1,2, Li Xinyang1*

1Key Laboratory of Adaptive Optics, Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China

The first 3 frames of wavefront recovery phase simulation data

Overview:In the actual adaptive optics control system, the time delay causes the mismatch between the correction profile generated by the corrector and the actual wavefront distortion, which leads to correction lag error. The longer the time delay, the worse the overall system control performance. Under the atmospheric frozen flow turbulence assumption, the atmospheric turbulence spatial characteristics will not change significantly in a certain time scale, and the atmospheric frozen flow turbulence is driven by the atmospheric transverse wind. According to the turbulence temporal aberration characteristics, a wavefront distortion prediction method based on motion estimation is proposed. Through the wavefront restored images of the reference frame and the current frame, the template matching algorithm can estimate the atmospheric turbulence motion direction, and then the current frame is moved to predict the next frame. Under the simulation conditions of the sampling frequency of 500 Hz, the wavelength of 550 nm, the telescope aperture of 1.8 m, and the phase screen numbers of 10, the overall ideal correction error of the 65 orders Zernike wavefront image can be reduced from 0.0614to 0.0508by predictive compensation, and the relative correction residual is 7.62%. Furthermore, the residual error is calculated with the template matching algorithm and the least recursive squares (RLS) algorithm to evaluate the prediction effect. By comparing different sampling frequencies and different transverse wind speeds, the method performs better when the variation tendency of wavefront restored images is obvious. Therefore, the prediction effect can be maintained better in severe conditions. Since the actual wavefront distortion deviates from the frozen flow turbulence assumption, two improved methods are proposed. The first one calculates the ideal prediction correction residuals, and the second one directly predicts the ideal correction residuals, which can further reduce the overall ideal correction error to 0.0343and 0.0242. Correspondingly, the prediction method is verified by using the actual observation data of Sirius, Hartmann sensor microlens array numbers of 156, the sub-aperture resolution of 16×16, the sampling frequency of 500 Hz, and backtracking frame numbers of 3. The overall ideal correction error promotion effects of the 65 orders Zernike wavefront image are 15.97% and 24.85% using two improved methods. Increasing the recovery area can slightly improve the prediction effect, but it is not proportional to the calculation cost. The experimental results fit the theoretical analysis well, which suggests that the algorithm has certain practical value and is helpful in actual adaptive optics control systems.

Zhou X, Li X YWavefront distortion prediction method based on motion estimation[J]., 2021, 48(10): 210288; DOI:10.12086/oee.2021.210288

Wavefront distortion prediction method based on motion estimation

Zhou Xin1,2, Li Xinyang1*

1Key Laboratory of Adaptive Optics, Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China

In the actual adaptive optics control system, the time delay causes the mismatch between the correction profile generated by the corrector and the actual wavefront distortion, which leads to correction lag error. Under the atmospheric frozen flow turbulence assumption, a wavefront distortion prediction method based on motion estimation is proposed to compensate for the time delay. The template matching algorithm is used to estimate the atmospheric turbulence motion direction, according to the wavefront restored images of the reference frame and the current frame, and then the current frame is moved to predict the next frame. The prediction method applicability is evaluated, and the influence of backtracking frames on the prediction effect is discussed by comparing the simulation data of different sampling frequencies and different transverse wind speeds. The residual error is calculated with the template matching algorithm and the least recursive squares (RLS) algorithm. The simulation results show that the method performs better when the variation tendency of wavefront restored images is obvious. Therefore, the prediction effect can be maintained better in severe conditions. Finally, the prediction method is verified by using the actual observation data of Sirius, and the algorithm still keeps the prediction effect.

adaptive optics; turbulence prediction; motion estimation; wavefront correction

National Natural Science Foundation of China (62005286)

10.12086/oee.2021.210288

TN929.1

A

* E-mail: xyli@ioe.ac.cn

周鑫，李新阳. 基于运动估计的波前畸变预测方法研究[J]. 光电工程，2021，48(10): 210288

Zhou X, Li X Y. Wavefront distortion prediction method based on motion estimation[J]. Opto-Electron Eng, 2021, 48(10): 210288

2021-09-06；

2021-10-26基金项目：国家自然科学基金资助项目(62005286)

周鑫(1997-)，女，硕士研究生，主要从事自适应光学技术方面的研究。E-mail：zhouxin97_2021@163.com

李新阳(1971-)，男，博士，研究员，主要从事自适应光学技术方面的研究。E-mail：xyli@ioe.ac.cn

版权所有©2021中国科学院光电技术研究所