QP980钢拉伸过程的晶体塑性模拟

杨 浩，汪华苗，李大永

(上海交通大学 机械与动力工程学院，上海 200240)

第三代先进高强钢(3G-AHSS)具有良好的强度和塑性，在车身结构件制造方面有广阔的应用前景[1].淬火配分(QP)钢[2]是一种典型的第三代先进高强钢，QP钢的室温组织一般为马氏体相与弥散分布的奥氏体相，对于部分奥氏体化的情况，其室温组织还含有铁素体相[3].QP钢的变形行为复杂，变形诱发的马氏体相变(DIMT)不仅使强度提高，而且能够增加相变诱导塑性(TRIP)[4].为了探究QP钢的变形行为，需要对其内部各组成相的微观性能和演化规律进行深入的研究.

以往研究从实验和理论建模的角度对QP钢的变形行为进行了分析.实验上，通过纳米压痕[5]、微柱压缩[6]、高能X射线衍射(HEXRD)[7]及中子衍射[8]等方法研究了QP钢中各相的力学行为以及相变动力学，或是采用不同温度、不同应变率[9]以及不同加载模式[10]研究了加载条件对相变行为及力学行为的影响.在理论建模方面，一般分为现象学模型和微观晶体塑性模型.其中，现象学模型一般从实验现象出发，首先建立与温度、应变率、应力三轴度及罗德角的相变动力学方程[11]，描述残余奥氏体相体积分数的演化规律，然后在本构模型中引入残余奥氏体体积分数项，从而建立考虑相变的现象学本构关系.现象学本构模型能够很好地描述材料的宏观变形行为，且计算效率高，但无法描述材料变形过程中微观结构的演化规律.晶体塑性模型从晶粒层面出发，首先通过晶粒内部微观变形机制建立单晶体本构关系，然后将单晶体通过自洽(SC)方式或有限元法(FEM)结合起来，从而描述多晶体的变形行为.目前针对QP钢的晶体塑性模型研究还较少，有的只讨论了宏观力学性能及各相微观力学性能，而没有讨论各相织构的演化过程[6]，有的甚至忽略了相变的影响，仅仅建立了多相结构的晶体塑性模型[12-13].

本文以QP980钢为研究对象，首先利用电子背散射衍射(EBSD)方法表征了材料的微观组织，包含铁素体、马氏体和残余奥氏体，并通过铁素体相和马氏体相灰度的差异将其分离，得到每一相的初始织构.然后基于马氏体相变晶体学唯象理论(PTMC)和弹-黏塑性自洽(EVPSC)多晶体塑性模型建立了考虑相变的多晶体塑性模型，模拟了QP980单向拉伸过程中的宏观流动应力和微观织构演化.在此基础上，定量分析了相变对QP980宏观流动应力和加工硬化率的影响.最后，通过计算材料变形过程中应变和应力的配分情况，分析了各相对宏观变形的贡献.

1 考虑相变的晶体塑性模型

1.1 单晶体本构模型

QP980初始存在铁素体、回火马氏体及残余奥氏体，相变后产生新生马氏体.其中，铁素体、回火马氏体及新生马氏体单晶的塑性应变率为所有滑移系塑性剪切率的总和[14-15]：

(1)

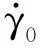
(2)

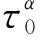
奥氏体单晶的塑性应变率还包括相变应变率，计算方法见下文.

1.2 相变模型

PTMC这一理论最早由Wechsler等[17]和Bowles与Mackenzie[18-19]分别提出，后经Wayman[20]系统总结.基于PTMC建立的相变模型总结如下：

(1)当奥氏体晶粒内部累计塑性剪切量达到临界值时，发生相变.

(2)由于QP980钢中残余奥氏体含量(指体积分数，下同)较少，含量约10%，新生马氏体对整体马氏体的织构影响较小.因此，为了提高计算效率，对于一个奥氏体晶粒，只允许相变势最大[21]的变体产生.

(3)新生马氏体作为一个新的晶粒，其初始轴比为10∶10∶1的椭球，初始应力状态与母相奥氏体晶粒相同，初始为弹性状态，弹性应变可由应力状态和弹性刚度阵计算.

(4)新生马氏体与母相奥氏体之间为Kurdjumov-Sachs取向关系，相变本征应变的计算方法参见文献 [22].

(5)新生马氏体的体积分数演化遵循O-C公式，具体为[23]

f=1-exp{-β2[1-exp(β1Γ)]β3}

(3)

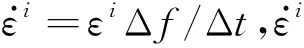
1.3 多晶体自洽模型

在自洽模型中，假设单个晶粒为椭球体，夹杂于一个均匀的等效介质体中，等效介质的力学性质是所有单晶的体积平均，通过Eshelby夹杂理论求解单晶体与等效介质间的相互作用，可以建立单晶与多晶体的相互作用方程：

(4)

2 微观结构

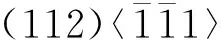
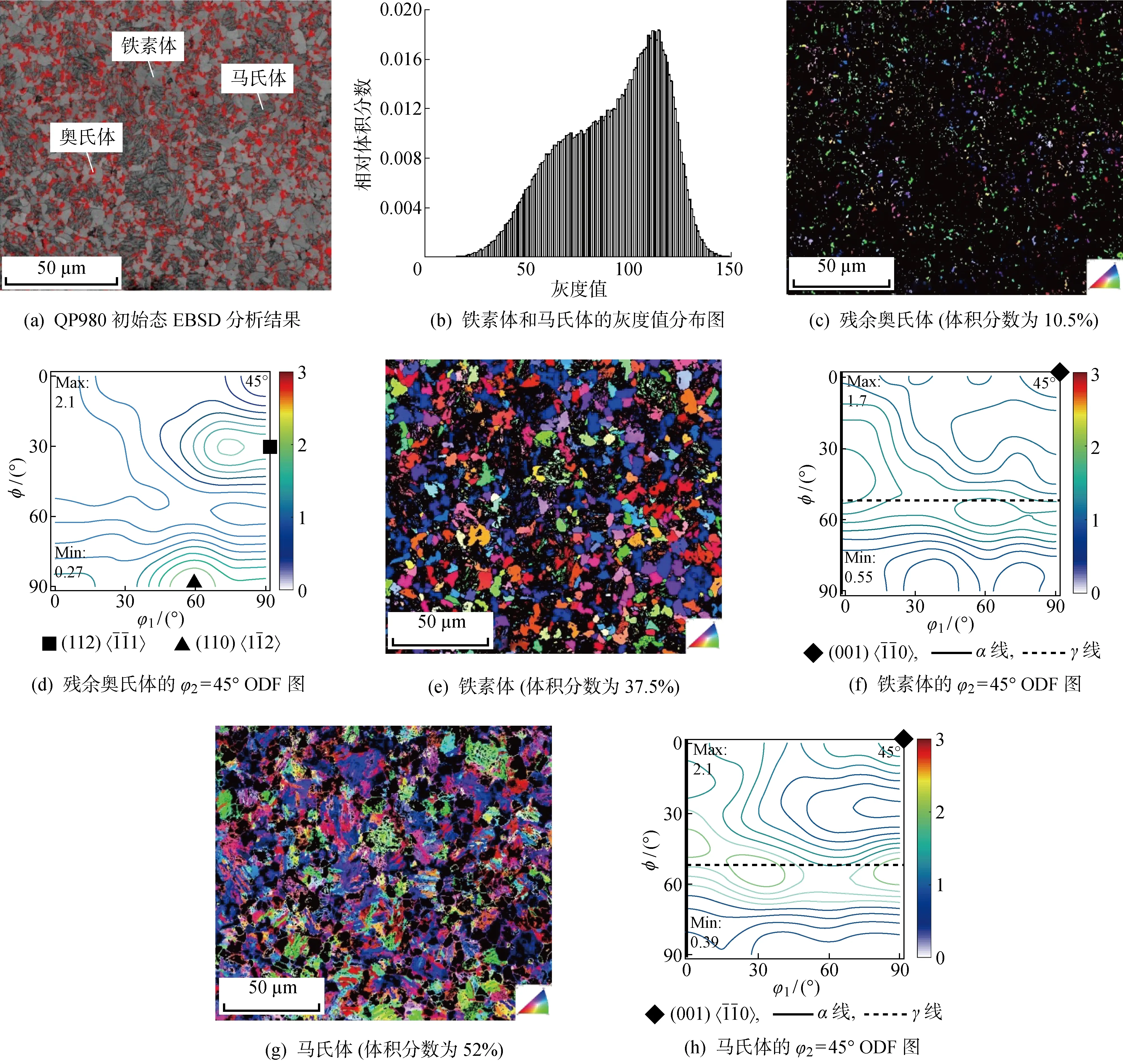
图1 QP980钢初始态EBSD分析结果及各相织构Fig.1 EBSD results of QP980 in the initial state and the textures of each phase

3 结果与讨论

3.1 宏观机械性能与微观结构演化

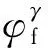
表1 各相硬化参数和残余奥氏体相变参数Tab.1 Hardening parameters of constituent phases and transformation parameters of austenitic phase

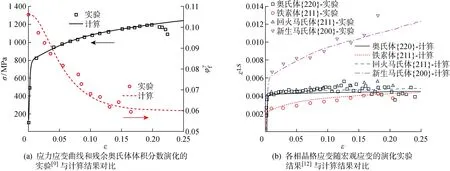
图2 模型计算结果与实验结果的对比Fig.2 Comparison of model calculation results and experimental results

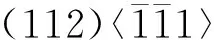
图3 应变量为0.15时的各相织构的计算结果与实验结果对比Fig.3 Comparison of calculated results of each phase texture with experimental results at a strain of 0.15

3.2 相变对宏观机械性能与微观结构演化的影响

通过关闭模型中相变部分，可以得到材料不发生相变时的力学行为和微观结构演化.相变对流动应力的影响见图4(a).相变对加工硬化率的影响见图4(b)，图中n为加工硬化率.可见，对于QP980冷轧钢板，相变能够明显增加材料的强度和加工硬化率.尽管随着应变的增加，硬化率逐渐降低，但相变能够延缓硬化率的降低速度.此外，计算结果表明相变对各相织构的演化几乎没有影响.

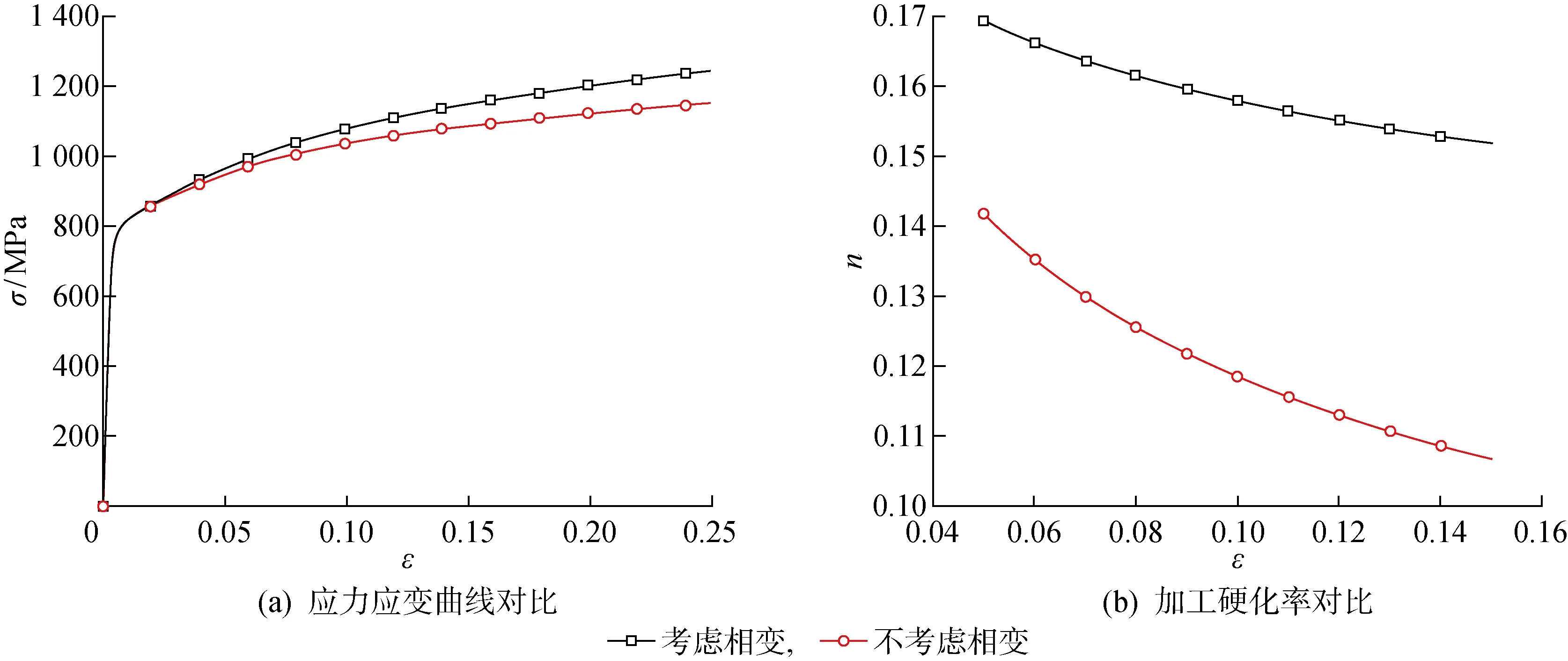
图4 相变对应力应变曲线和加工硬化率的影响Fig.4 Effect of phase transformation on stress strain curve and work hardening rate

3.3 各相对塑性变形的贡献及微机械性能

各相的平均等效应力随宏观等效应变的变化如图5(b)所示，图中σeq为von Mises等效应力.残余奥氏体的屈服强度约为600 MPa，铁素体的屈服强度约为490 MPa，而回火马氏体的屈服强度约为 790 MPa，新生马氏体的屈服强度约为920 MPa.在变形初期(变形量小于5%)，铁素体的等效应力最低，残余奥氏体的等效应力次之.随着变形量的增加，铁素体内的等效应力会逐渐超过残余奥氏体的等效应力，说明铁素体的硬化速度比奥氏体的硬化速度更快.回火马氏体在整个变形过程中几乎不发生硬化，接近理想弹塑性，而新生马氏体在整个变形过程中始终保持较高的应力和硬化速度，最有可能是断裂的萌生位置.

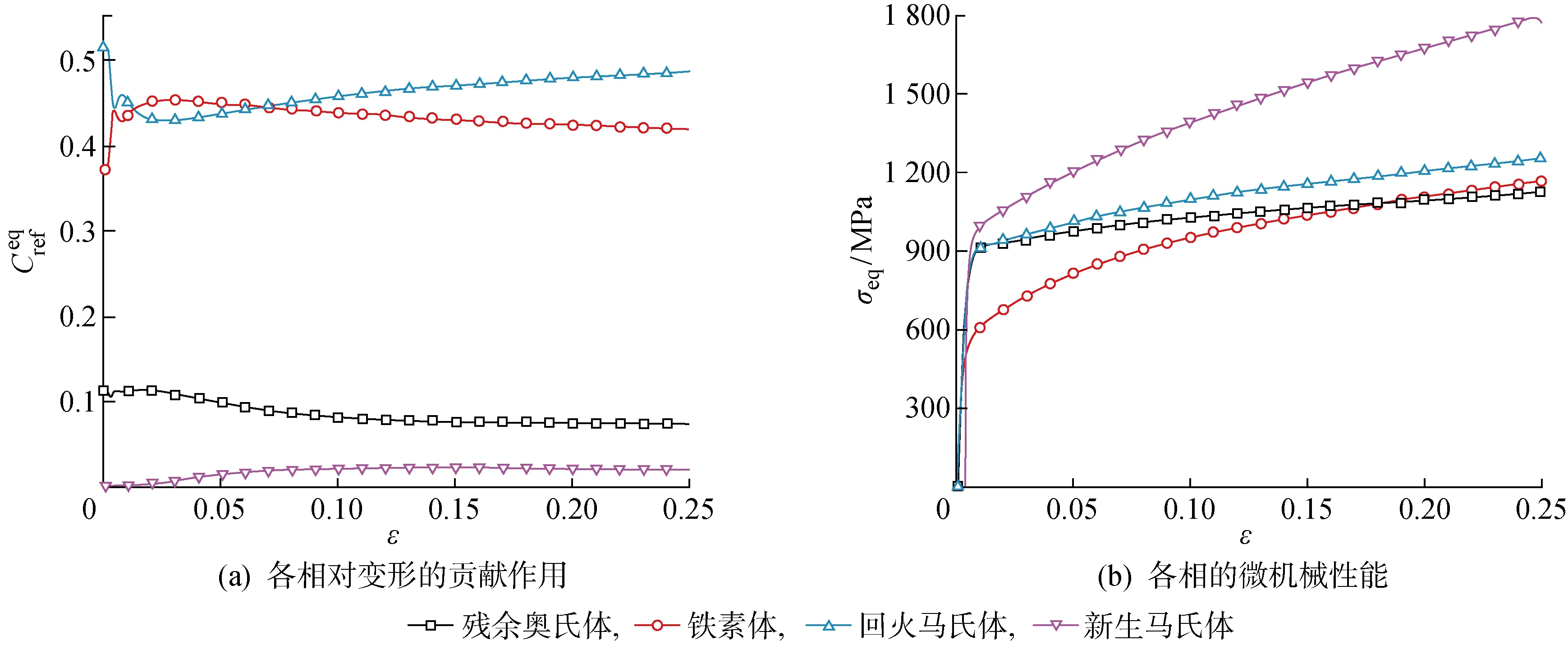
图5 各相对变形的贡献作用和微机械性能Fig.5 Contribution of each phase to deformation and micro-mechanical properties of each phase

4 结论

基于PTMC和EVPSC框架，建立了考虑相变的微观本构模型，并以第三代先进高强钢QP980为研究对象，模拟了单向拉伸变形中宏观流动应力和织构演化过程，研究了相变对流动应力和织构演化的影响以及各相的微机械性能对塑性变形的贡献，结果如下：

(1)QP980冷轧钢板初始包含铁素体(37.5%)，马氏体(52%)和残余奥氏体(10.5%)，各相均为典型的轧制织构，在沿着轧制方向拉伸变形后，残余奥氏体〈111〉丝织构、铁素体和马氏体的〈110〉丝织构有明显的增强.

(2)相变能够明显增加QP980钢的强度和加工硬化率，而对材料织构演化几乎没有影响.

(3)铁素体和回火马氏体对QP980的塑性变形起主要作用，变形过程中新生马氏体的应力最大，可能成为断裂的萌生位置.