基于GSFA-GNPE的动态-静态联合指标间歇过程监控
赵小强,牟 淼
(兰州理工大学 a.电气工程与信息工程学院;b.甘肃省工业过程先进控制重点实验室;c.电气与控制工程国家级实验教学示范中心,兰州 730050)
随着对生产过程安全性和产品质量要求的日益增长,过程监控受到越来越多的关注[1-2].近年来,多元统计过程监控(MSPM)方法被广泛应用于过程监控,其主要思想是将高维数据投影到低维空间,并保留原始数据的主要信息[3-5].
传统的MSPM方法,如主成分分析(PCA)和邻域保持嵌入(NPE)等[6-9],假定在不同时间的样本是独立的,即过程当前时刻的状态不受之前时刻的影响,然而在现代工业中这种假设是不成立的,因此传统的监控模型无法准确表达过程数据的动态特性.为解决这一问题,文献[10]利用包含当前和过去时刻采样值的增广矩阵进行建模,提出了动态主元分析(DPCA)方法.然而,DPCA方法本质是一种全局结构保持方法,忽略了局部信息的提取,为此,NPE等局部流形算法被用于过程监控.NPE通过保持数据的局部邻域结构来实现数据降维,其假设数据样本满足独立分布,主要关注数据的空间结构特征,能有效提取数据的静态信息,但NPE算法忽视了数据随时间变化的特征信息,可能会造成检测效果不佳.为了有效提取过程数据的动态信息和局部信息,文献[11]在邻域保持嵌入算法保持数据局部结构的基础上引入时序扩展,提出一种基于时序扩展的邻域保持嵌入(TNPE)算法用于动态过程建模,一定程度上提高了动态过程的故障检测效果.但是,上述方法假设生产过程的所有变量均具有动态特性,并没有综合考虑生产过程中的静态变量.同时,NPE作为流形算法,其降维时主要考虑数据的局部结构特征会造成全局信息的丢失.因此,有必要为NPE算法加入全局目标函数加以约束,使其能充分提取过程信息.
近年来,慢特征分析(SFA)被用于过程监控[12-15],SFA的主要思想是从时间序列中提取缓慢变化的特征[16],能够有效提取表征过程数据动态变化的慢特征.文献[17]将SFA方法扩展到质量相关的故障检测领域,提出了一种基于SFA的工业过程质量相关故障检测算法.文献[18]将核方法应用于慢特征分析,提出了一种核慢特征判别分析(KSFDA)和支持向量数据描述(SVDD)的故障检测方法,对于非线性过程具有较好的检测效果.然而在实际工业过程中,一些过程变量可能是动态的,而另外一些则是静态的.尽管基于SFA的故障检测算法在动态工程监控中取得了长足的进步,但SFA未能同时考虑过程的动态特性和静态特性.对于动态变量,动态特征能够通过变量的动态变化准确地进行提取;而对于静态变量,动态信息则是由随机噪声引起的,提取的动态特征是与噪声相关的特征,与过程数据无关.此外,随机噪声可能会随着基准数据集的不同而变化,因此不需要在静态变量中进行动态特征提取.同时,将SFA应用于间歇过程监控时,由于间歇过程在进行数据展开时会破坏其原始时间结构信息,需要根据最近邻准则构造伪时间序列以提供时间结构信息,这就使得SFA等价于一种局部近邻数据关系保持算法,而忽略了全局结构信息.因而,需要将全局结构分析融入SFA,使其能充分提取过程信息.
将所有过程变量都视为静态变量用静态方法,或都视为动态变量用动态方法进行监控,都会导致故障监控效果不佳,且单一考虑全局信息或局部信息都会造成过程信息丢失.鉴于SFA和NPE在处理动态数据和静态数据方面各自的优势,提出一种基于全局慢特征分析(GSFA)-全局邻域保持嵌入(GNPE)的动态-静态联合指标间歇过程监控方法.首先,计算每个变量的自相关系数和互相关系数,分别求得当前时间和过去时间的变量之间的相关性以及当前时间的变量和过去的另一个变量之间的相关性.在此基础上,将过程变量分为动态子空间和静态子空间.在动态子空间中建立GSFA模型,提取动态全局信息;在静态子空间中建立GNPE模型,提取静态全局信息.最后,将两个子空间得出的监视统计信息进行贝叶斯推断,得出联合指标以进行故障检测.本文方法通过将过程变量区分为动态变量和静态变量,在不同的变量空间中采用不同的方法进行建模,可以充分提取过程信息,有效提高对于间歇过程的监控效果.
1 基础算法
1.1 慢特征分析算法
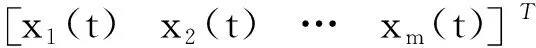
SFA算法的优化问题可用如下形式表示:
(1)
s.t.〈si〉t=0
(2)
(3)
∀i≠j:〈sisj〉t=0
(4)
i,j=1,2,…,m
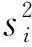
(5)
SFA算法通过将正常数据中提取出的慢特征进行线性转化,该过程可表示如下:
(6)
i=1,2,…,m
式中:wi为负载向量.慢特征可表示为
s=Wx
(7)

在进行SFA算法计算时,首先利用奇异值分解进行白化操作以消除变量之间的相关关系,令R=〈x(t)x(t)T〉t为x(t)的协方差矩阵,R的奇异值分解可写为
R=UΛUT
(8)
式中:Λ为特征对角阵;U为特征矩阵.白化矩阵可以表示为Q=Λ-1/2UTx,则白化过程可用如下形式表示:
z=Λ-1/2UTx=Qx
(9)
由式(7)和(9)可得:
s=Wx=WQ-1z=Pz
(10)
式中:P=WQ-1.显然〈zzT〉t=Q〈xxT〉QT=I,I为单位矩阵且〈z〉t=0,又由于约束式(2)和(3)的存在,可以得到如下表达式:
〈ssT〉t=I
(11)
则式(11)可写为
〈ssT〉t=P〈zzT〉PT=PPT=I
(12)
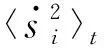
(13)
i=1,2,…,m
式中:pi为特征向量.在实际过程中,样本数据是在离散的时间状态下采集到的,基于时间的导数可以由差分近似计算如下:
(14)
i=1,2,…,m
式中:Δt为时间间隔.通过使用协方差矩阵的奇异值分解来解决优化问题,在这种情况下,奇异值分解可以表示为
(15)
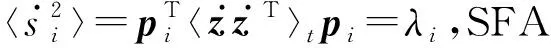
SFA负载矩阵的计算可由下式表示:
W=PQ=PΛ-1/2UT
(16)
1.2 邻域保持嵌入算法
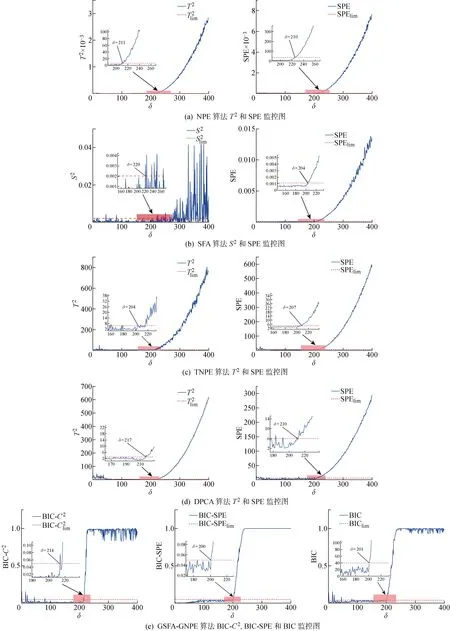
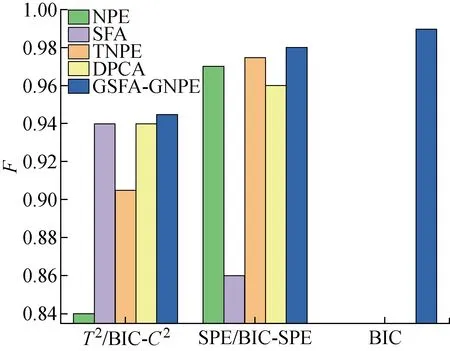
对于原始数据矩阵X∈Rn×m,n为样本个数,NPE通过计算投影矩阵A将X投影到低维空间Y∈Rn×d,其中,d (17) j=1,2,…,k 式中:xi为原始样本点;Mij为样本点xi与其近邻xj间的权值;M为权值矩阵;k为近邻个数. NPE算法的思想是若在高维空间中Mij可以重构样本xi,则在低维空间中可通过相同的权值来重构对应低维空间样本点yi,特征映射可通过最小化目标函数求解: (18) i=1,2,…,n;j=1,2,…,k 式中:yi为原始样本投影到低维空间的样本点,aN为NPE的投影矩阵A的列向量.aN可以通过求解下式的广义特征值获得: XZXTaN=λXXTaN (19) 式中:Z=(I-M)T(I-M).求解获得最小的d个特征值(λ1≤λ2≤…≤λd)所对应的特征向量[aN1aN2…aNd]T组成的投影矩阵A. 动态变量是指随时间快速变化的变量,静态变量是指在一段时间内相对恒定的变量.对于原始数据矩阵X=[x1x2…xn]∈Rn×m,变量xi和xj的互相关系数可以表示为 (20) i,j=1,2,…,m (21) 2.2.1全局慢特征分析算法 间歇过程三维数据展开示意图如图1所示,其中:Xi为某一批次的数据矩阵;N为批次数;J为变量数;K为采样时刻数.展开后的数据矩阵X(N×J×K)由一系列的时间切片矩阵Xk(N×J)(k=1,2,…,K)组成,这种展开方式破坏了矩阵X(NK×J)中蕴含的时间序列信息.在GSFA建模时,利用数据近邻点的结构信息构造伪时间序列提供时间序列结构信息.对于样本点xk,i的伪时间序列可表示为 图1 间歇过程三维数据展开示意图Fig.1 Schematic diagram of 3D data expansion in batch process (22) 更进一步地,可以用如下形式表示时间切片矩阵Xk(N×J)的伪时间序列矩阵: (23) 在此基础上,X(NK×J)就被扩展成一个如下式所示的伪时间序列矩阵: (24) 对于1≤j≤NKl,用τ2j-1和τ2j表示伪时间序列T中的第2j-1和第2j个样本点,因此,在样本点τ2j-1和τ2j之间可以认为存在时间变化.伪时间序列T的时间变化矩阵ΔT可以表示为 (25) SFA的目标函数可用如下形式表示: (τ2j-τ2j-1)Twj= (26) 式(26)是最小化输出信号的时间变化,由KNN准则构造伪时间序列T(2NKl×J),当在间歇过程处理数据时,SFA 被认为是局部处理方法,因为其仅保留了本地邻域关系而忽略的数据全局结构.为此,提出一种全局慢特征分析算法,在保留邻域信息的基础上分析数据的全局结构. (27) (28) 为了保持局部邻域信息和全局结构,GSFA目标函数可以表示为 ΦGSFA=βΦSFA-(1-β)ΦG= (29) j=1,2,…,J 式中:0≤β≤1为松弛因子,用于平衡全局函数和局部函数的比重;L=ΔTΔTT.考虑到正交约束在建立统计量中的优越性,施加以下正交约束: 等式中两个目标函数的尺度不同,需要进行标准化,标准化后的目标函数为 (30) 求解式(30)的最优化问题等价于求解下式的特征值问题: (31) 根据GSFA模型提取前p个慢特征信息后构建S2和平方预测误差(SPE)统计量进行监控,定义如下: (32) (33) 本文采用的核密度函数表达式如下所示: (34) (35) (36) 式中:SPEj、Sj为第j个SPE和S2统计量. 2.2.2GNPE算法 NPE算法在降维过程中只考虑了数据的局部结构,忽略了数据的全局结构信息.为了同时考虑全局和邻域结构,在静态子空间中建立GNPE模型,充分表征故障信息,其中全局结构通过寻找方差最大来保持,其目标函数如下所示: (37) j=1,2,…,NK GNPE算法的目标函数为 (38) (39) 进一步转换为特征值分解问题: Gdi=λiRdi 由最大的g个特征值(λ1≤λ2≤…≤λg)对应的特征向量[d1d2…dg]构成投影矩阵D. GNPE算法将静态空间分为特征空间和残差空间,构造T2和SPE统计量对过程进行监控,其表达式如下所示: (40) SPE=‖xnew-Dynew‖ (41) ynew=DTXnew (42) 2.2.3联合指标建立 通过计算相关矩阵,将过程变量分为ΩD和ΩS两个子空间,在动态子空间ΩD进行GSFA建模,计算S2和SPE统计量,在静态子空间ΩS进行GNPE建模,计算T2和SPE统计量.为了实现对静态子空间和动态子空间的联合监控,通过贝叶斯推断建立一个联合指标,以实现对整个间歇过程的监控.在动态子空间ΩD中,S2的故障条件概率定义为 (43) (44) (45) 同理,可计算求得PSPE(F|ΩD)、PSPE(F|ΩS)和PT2(F|ΩS),其中:PSPE(F|ΩS)为动态子空间中SPE的故障概率;PSPE(F|ΩS)为静态子空间中SPE的故障概率;PT2(F|ΩS)为静态子空间中T2的故障概率.动态子空间中S2统计量和静态子空间中T2统计量可建立BIC-C2指标,动态子空间和静态子空间中的SPE统计量可建立BIC-SPE指标,则有: (46) (47) 联合指标BIC由如下表达式建立: BIC= (48) 联合指标BIC-C2、BIC-SPE和BIC的控制限为1-α. 基于GSFA-GNPE的动态-静态联合指标间歇过程监控方法包括离线建模和在线监测两个阶段,如图2所示. 图2 基于GSFA-GNPE的动态-静态联合指标间歇过程监控Fig.2 Batch process monitoring of dynamic-static joint indicator based on GSFA-GNPE (1)离线建模步骤如下. 步骤1将采集到的正常工况的三维数据矩阵X(N×K×J)展开为X(N×KJ),进行标准化处理后排列成X(NK×J); 步骤4在划分完成的动态子空间中进行GSFA建模,在静态子空间中进行GNPE建模; (2)在线监测步骤如下. 步骤1对测试样本Xtest进行标准化处理; 步骤2根据离线建模步骤3的结果将过程变量分为动态变量ΩDnew和静态变量ΩSnew; 采用如下数值例子验证所提算法[21]: (49) y(i)=z(i)+v(i) (50) (51) (52) 式中:h为在[-2,2]上均匀分布的输入向量;输入n=[n1n2n3]为一个随机向量,n1、n2均匀分布在[-1,2]上,n3均匀分布[0,3]上;v为均值为0、方差为0.1的噪声.输出y、k和u是可测量的,使用8个变量(y1,y2,y3,u1,u2,k1,k2,k3)的400个样本进行模型训练.显然,前5个变量是动态的,而后3个变量是静态的,所监测的故障从第200个采样点引入至第400个采样点结束,故障描述如下: 故障1h2处引入值为2的阶跃故障; 故障2n1处引入值为3的阶跃故障. 对采集到的400个样本首先对每个变量计算顺序相关矩阵,选择时间延时γ为2[10].根据统计学理论[22],一旦两个变量的相关系数绝对值小于0.3,则两个变量不再相关,故本文选择阈值η为0.3.每个顺序相关矩阵中的最大值如表1所示,其中加粗的数据为大于0.3的数值.由表1可以看出,前5个变量顺序相关矩阵中的最大值均大于0.3,被划分为动态变量,其余变量被划分为静态变量,这与所提数值例子变量关系相符.将GSFA-GNPE算法与SFA算法和NPE算法用于数值例子故障检测,置信度α=0.98.3种算法对故障1和故障2的检测率和误报率如表2所示.由表2可知,GSFA-GNPE算法的检测效果优于SFA算法和NPE算法. 表1 相关系数矩阵的最大值Tab.1 Max values in cross-correlation matrix 表2 3种算法对故障1和故障2的检测率和误报率Tab.2 Detection rates and false alarm rates of three algorithms for Fault 1 and Fault 2 3种算法对故障1的监控图如图3所示,其中:δ为采样时刻.NPE算法对故障1的T2和SPE监控图如图3(a)所示.从图3(a)中可以看出,NPE算法在采样时刻0~200之间存在大量报警,而0~200时刻为正常时刻,故NPE算法在该阶段存在大量误报警,误报率达19%,且在故障发生时刻200~400之间,有许多采样点统计量在控制限以下,没有及时全面的发出警报.图3(b)为SFA算法对故障1的S2和SPE监控图.从图3(b)中可以看出,在0~200采样点间,SFA算法存在较多的误报,有大量点超过了控制限,且在200~400采样点间有许多漏报.图3(c)为GSFA-GNPE算法的BIC-C2,BIC-SPE和BIC联合指标监控图.从图3(c)中可以看出,BIC-C2和 BIC-SPE在 0~200 之间只存在少量误报,且在200~400采样点间其检测率均高于SFA算法和NPE算法,BIC联合指标的检测效果最好,不仅其误报率极低,且检测率也达到了99%.综合对比3种算法对于数值例子故障的检测效果,本文所提的GSFA-GNPE算法误报率极小且检测率最大,监控效果最优. 图3 3种算法对故障1的监控图Fig.3 Monitoring chart of Fault 1 by three algorithms 本文进一步采用美国伊利诺伊州立理工学院开发的Pensim2.0青霉素发酵过程标准仿真平台得到的过程数据进行仿真验证[23],该平台可以通过设定不同但都在正常范围内的初始条件,模拟青霉素发酵过程中各变量每个时刻的数据用于分析研究,设定时间为400 h,采样时间为1 h,生产30个批次生长工况数据,并从18个变量中选择10个变量作为监控变量得到数据矩阵X(30×10×400)作为训练样本,如表3所示.故障种类和故障参数设置如表4所示.本文给出5种算法在故障2下的监控图,理想的监控图为在正常阶段(0~200采样点)所有统计量均在控制限以下,在故障阶段(200~400采样点)所有统计量均在控制限以上. 表3 过程变量Tab.3 Monitoring variables 表4 故障类型Tab.4 Fault types 在进行GSFA-GNPE建模时,松弛因子β用来平衡数据的局部邻域信息和全局结构信息,作为一个多目标优化问题,β很难找到一个绝对的最优解.因此为了平衡局部信息和全局信息,本文选取β=0.5,相关性阈值η=0.3,时间延迟γ根据文献[24]中的自相关函数法选取γ=17,邻域数k根据经验取k=6,核窗宽控制核函数的径向作用范围,本文通过交叉验证法设置θ=2 000.降维维数的确定在过程监控邻域目前尚没有主流的通用方法,本文需将所提算法与DPCA进行比较,因此本文选择与DPCA相同的降维维数,在建立DPCA模型时使用主元贡献度准则确定降维维数,GSFA建模时保留的慢特征数p=6,T2和SPE统计量的统计置信度和贝叶斯推断的置信度均为99%. 根据式(21)计算出顺序相关矩阵,将青霉素发酵过程的10个变量进行动态变量和静态变量的划分,其中变量序号为1、2、4、6、7、8的变量被划分为动态变量,序号为3、5、9、10的变量被划分为静态变量.5种算法对4个故障批次的故障检测率如表5所示. 表5 青霉素发酵过程中4个故障批次故障检测率Tab.5 Fault detection rates of four failed batches during penicillin fermentation NPE、SFA、TNPE、DPCA和GSFA-GNPE算法在故障2下的监控图如图4所示,故障2为搅拌功率从第200个采样点开始到第400个采样点结束的斜坡故障.由图4(a)可以看出,NPE算法的T2和SPE分别在第210和211个采样点检测出故障,且T2在0~50采样点间存在误报,因此NPE算法对于故障2存在较大的误报及故障检测延时.图4(b)为SFA算法的S2和SPE监控图.从图4(b)中可以看出,S2在第220个采样点才检测出故障发生,且在50~100采样点之间存在较多的误报,SPE在第204个采样点较早检测出故障,且在0~200采样点之间无误报发生.图4(c)为TNPE算法的T2和SPE监控图.从图4(c)中可以看出,TNPE算法的检测延时相较于NPE算法有所降低,原因是TNPE考虑了过程数据的时序特征,但在0~50采样点之间仍存在较多误报.图4(d)为DPCA算法的T2和SPE监控图.从图4(d)中可以看出,DPCA算法检测延时较高且误报也较多,检测效果不佳.图4(e)为GSFA-GNPE算法的BIC-C2,BIC-SPE和BIC联合指标监控图.从图4(e)中可以看出,BIC-C2在第214个采样点检测出故障,且在0~50采样点间有少量故障,而BIC-SPE统计量在故障一发生就立即检测到了故障,且全程无误报漏报,联合指标BIC也在第201个采样点处立即检测出了故障发生,基本不存在检测延迟.通过综合分析5种算法在故障2下的检测率和误报率,GSFA-GNPE算法有着更好的检测效果,原因是GSFA-GNPE算法分别考虑了过程数据的动态特性和静态特性,且针对两种特性分别采取了不同的方法进行监控,在提取数据局部信息的基础上分析了其全局结构,能够更加全面地捕捉数据特征,因此能够及时有效地反映过程故障.5种算法对4种故障的平均故障检测率F如图5所示.由图5可知,GSFA-GNPE算法的3种指标均有良好的检测效果,进一步说明了本文所提算法的有效性. 图4 5种算法对故障2的监控图Fig.4 Monitoring chart of Fault 2 by five algorithms 图5 青霉素发酵过程中4个故障批次的平均故障检测率对比Fig.5 Comparison of average fault detection rates of four failed batches during penicillin fermentation 本文提出一种基于GSFA-GNPE算法的动态-静态联合指标间歇过程监控方法.通过计算顺序相关矩阵,将过程变量划分为动态子空间和静态子空间,并在其中使用对应的算法进行统计分析.在动态子空间中,使用GSFA方法充分提取过程的动态特征,并且通过全局结构分析提取其全局信息特征;在静态子空间中,GNPE方法通过方差最大保持数据的全局结构,同时发挥NPE的局部结构保持能力,能有效提取过程数据的静态信息.然后,使用贝叶斯推断建立联合指标监控整个间歇过程.最后,将本文所提算法应用到数值实例和青霉素发酵仿真过程,研究结果显示所提出的GSFA-GNPE算法具有良好的监控效果.2 基于GSFA-GNPE动态与静态变量的间歇过程故障检测
2.1 动态变量与静态变量的区分
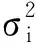
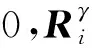
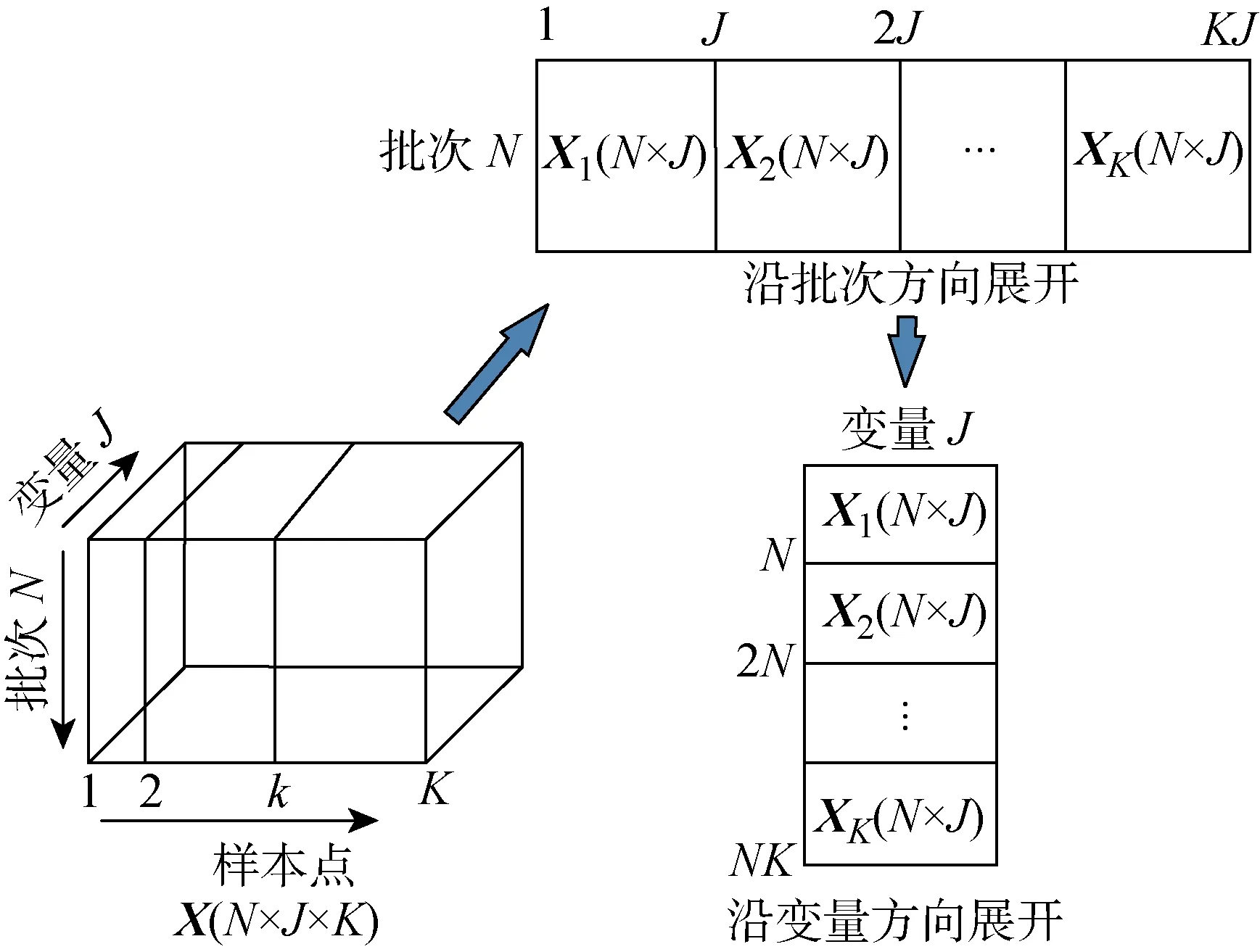
2.2 基于GSFA-GNPE动态与静态变量的间歇过程故障检测
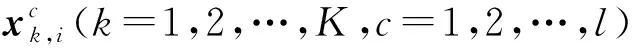
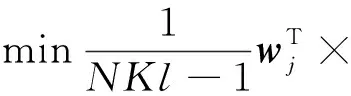
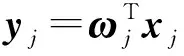
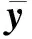
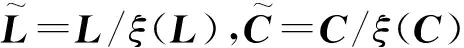
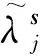
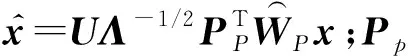
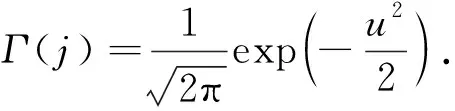
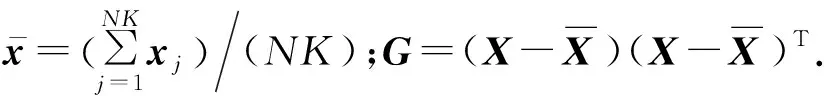
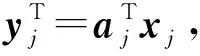
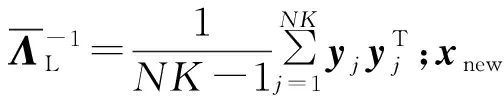
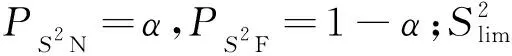
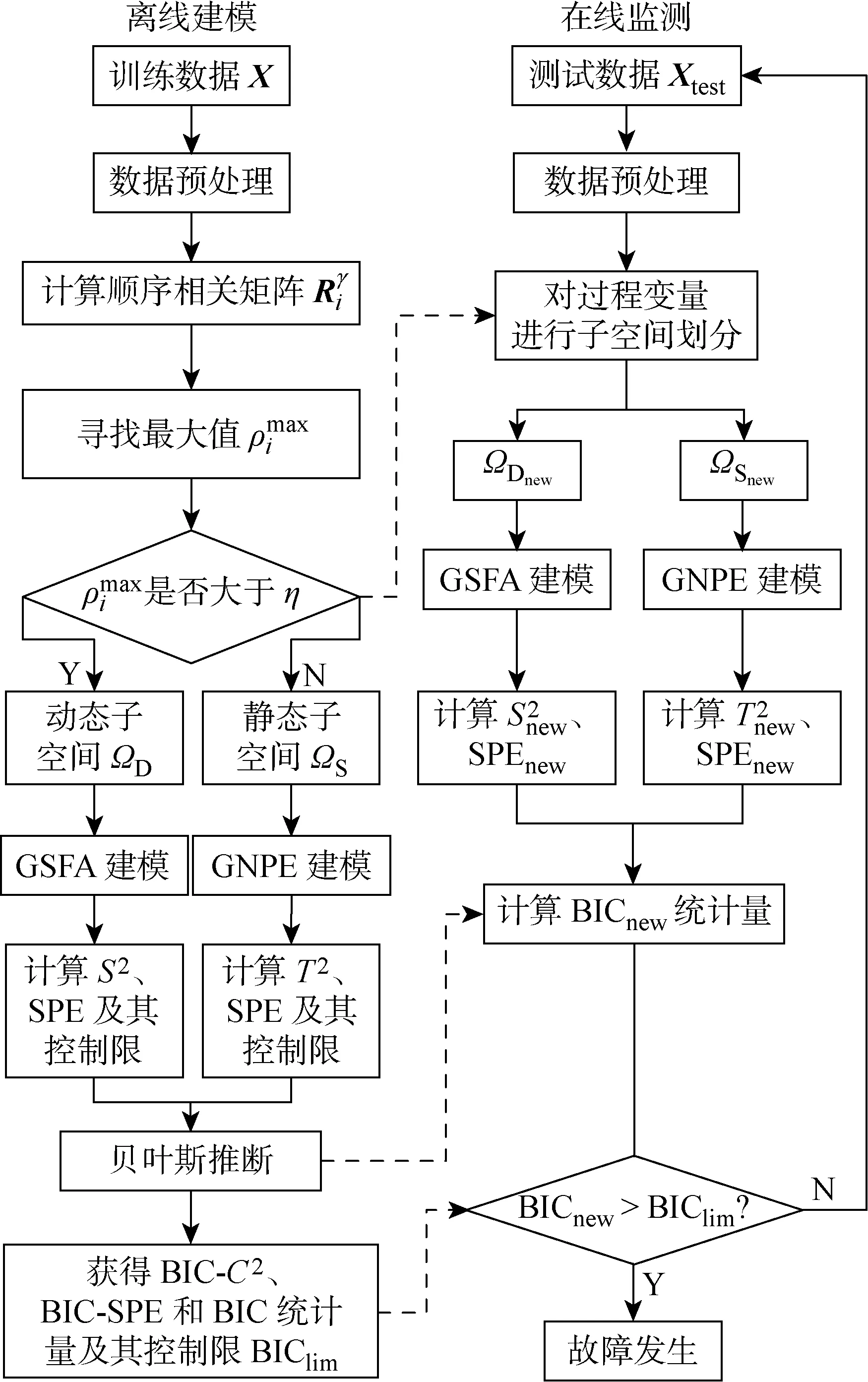
3 基于GSFA-GNPE的动态-静态联合指标间歇过程监控步骤
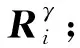
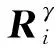
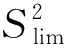
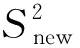
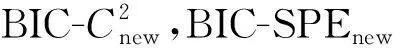
4 仿真实验
4.1 数值例子仿真
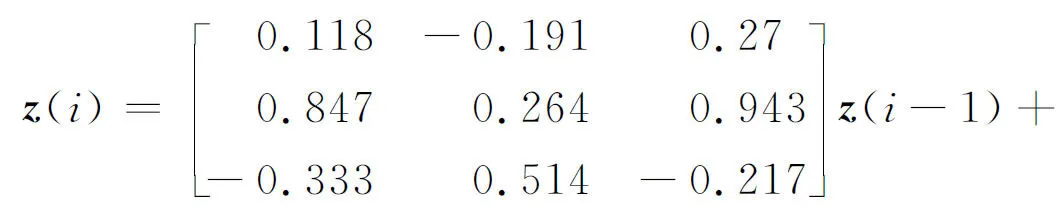
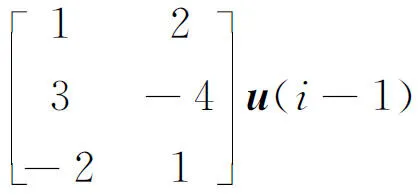

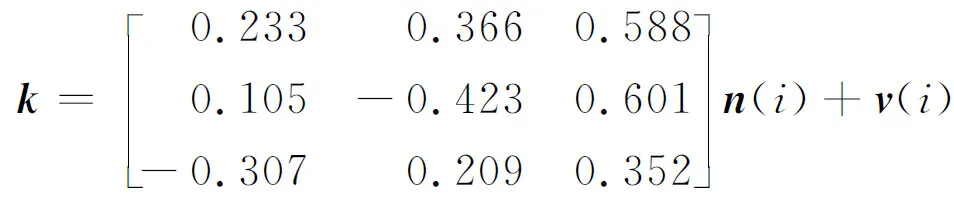
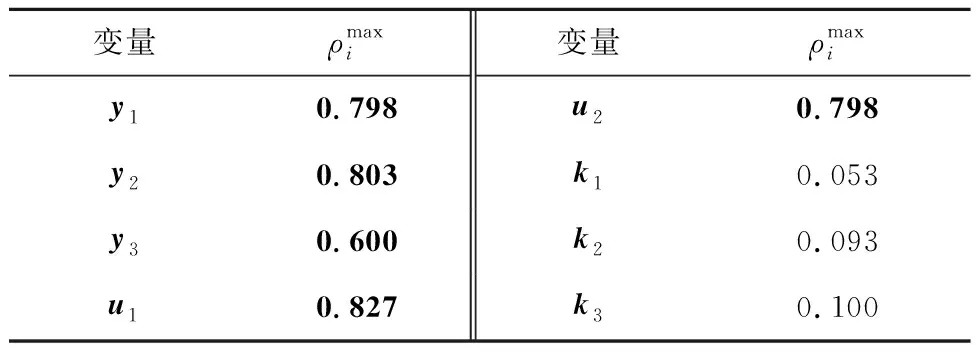

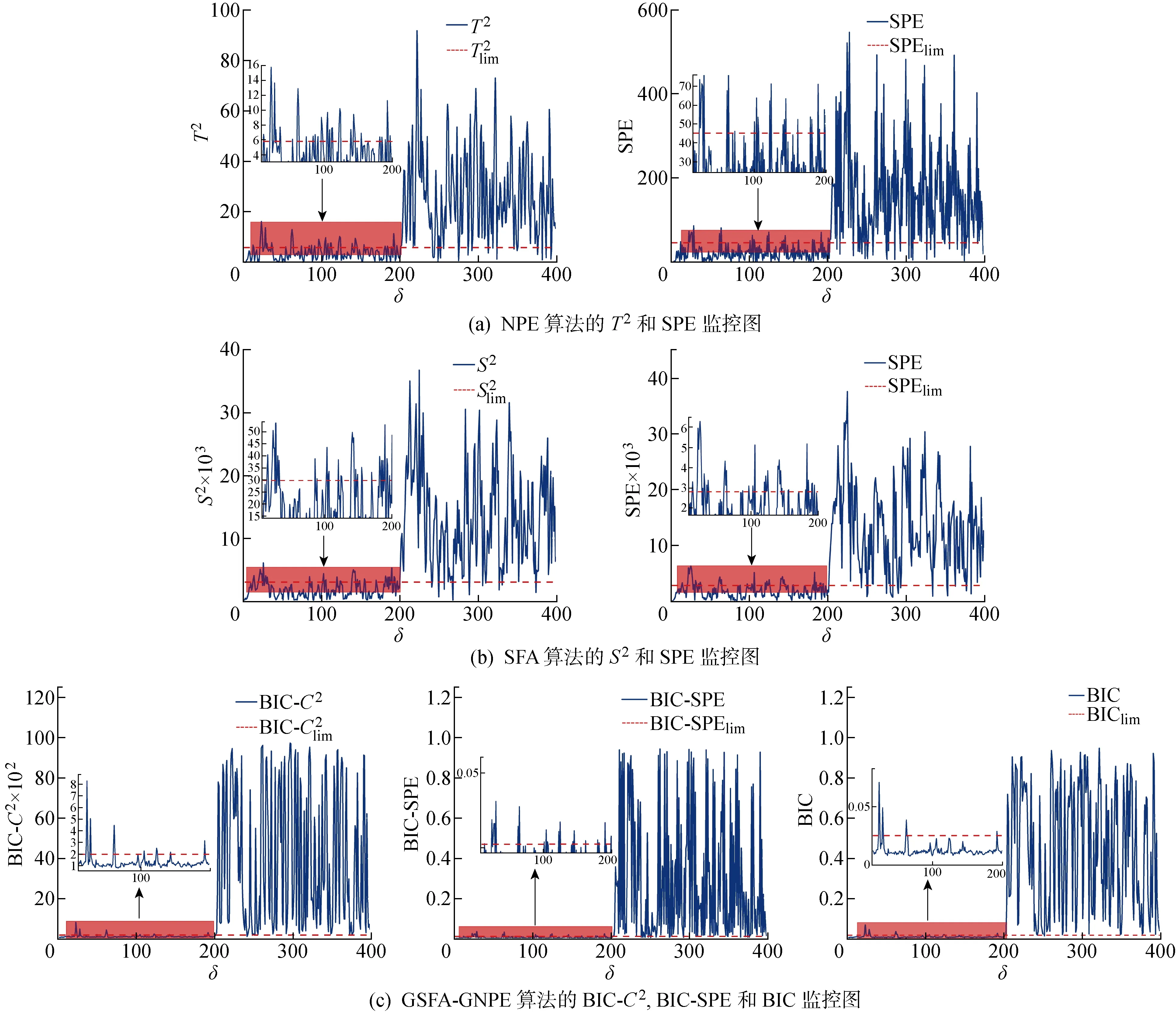
4.2 青霉素发酵过程
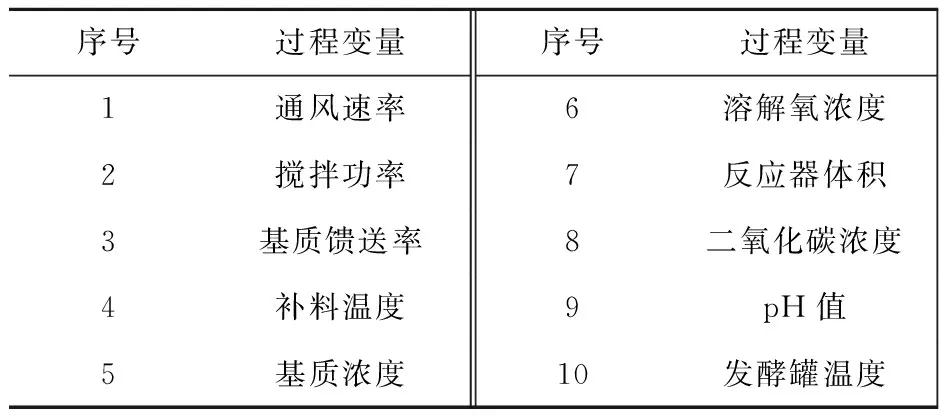
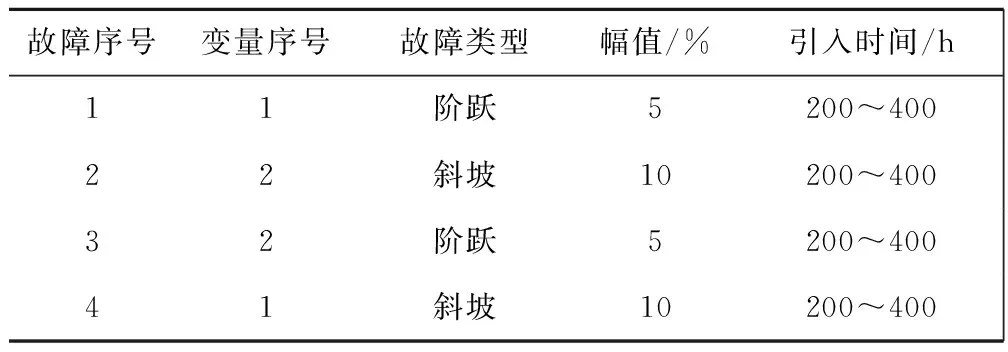

5 结语

