压气机退失速控制的数值仿真

高 原，吴亚东,b，欧阳华,b

(上海交通大学 a.机械与动力工程学院;b.燃气轮机与民用航空发动机教育部工程研究中心，上海 200240)

轴流压气机的不稳定工况主要分为以周向不均匀的高频扰动为特征的失速工况和以轴向传播的低频高振幅扰动为特征的喘振工况.失速时性能恶化，效率骤减，机械振动加剧.喘振时情况更为恶劣，发生超温、强振，甚至会导致压气机毁坏[1].因此，在实际应用中，需要极力避免压气机进入喘振或失速.一旦进入喘振或失速后，需要采取措施快速有效地退出.

通过对压缩系统不稳定工况的不断探索，研究者总结出一个衡量压缩系统稳定性的无量纲参数即B参数，以预测压缩系统不稳定工况的表现形式.B参数较大时，压缩系统表现为喘振工况，B参数较小时，压缩系统表现为失速工况.另外，根据压气机退出失速恢复到稳定工况时的流量是否大于其进入失速工况的流量，可以将压气机的失速工况分为存在滞后性和无滞后性.本文中研究存在滞后的失速.在以往的研究中，吴艳辉[2]使用由Moore和Greitzer合作完成的MG模型和单通道数值模拟对不同压缩系统过失速后能否成功退出失速做了对比，验证了转速越高时越难以退出失速的结论，与实验结果吻合良好.马彩东等[3]通过实验在失速后缓慢开启节流阀，绘制出退失速的迟滞曲线，并观察到失速工况的两个失速团在周向上先尺度减小，然后合二为一，最后经过3转消失，压气机退出失速.Hickman等[4]用实验得到了某跨音速单级压气机进失速和退失速的失速迟滞性能曲线，其中对于周向压力信号，失速团稳定时转速为0.53倍转子转速，在信号接近稳定时，扰动尖峰前点周向传递速度增加到0.73倍转子转速，而后点增加到0.56倍.李志平等[5]使用MG模型对比了两组低速压气机不同转速的性能曲线，认为其失速迟滞曲线的拓扑不变，失速与尖点突变模型能映射到统一模型线上.以上研究分别从退失速过程的实现条件、流场变化、信号波动及拓扑一致性进行了细致的分析.

在分析退失速过程时，对于压缩系统的动态仿真，MG模型[6]能够在一定程度上准确预测由进口管道、压气机、出口管道、稳压室及节流阀组成的压缩系统的动态性能.其关键是取平均半径位置的周向平均参数，并将扰动视为入口的一个幅值变化的正弦波，最终对压力平衡方程和质量守恒方程进行变换，再进行Galerkin近似后得到表示总压系数、流量系数及扰动幅值随时间变化的3个常微分方程.Mansoux等[7]取消了周向平均的假设，以傅里叶变换对扰动进行周向分解，最终将方程写成矩阵形式，一方面能得到周向流量的变化情况，另一方面提高了结果的精度.Gravdahl等[8]在经典MG模型的基础上加上了转速变化，引入转子动态方程，在原有的常微分方程中加入由转速变化而新产生的项，并加入可代表转速的B参数随时间变化的第4个常微分方程.这些MG模型在不断发展的同时，也得到了广泛应用.Sari等[9]利用变转速MG模型对失速发展结果进行对比，发现阀门应与转速协同控制才能更好退喘.苏三买等[10-11]等对MG模型进行了一系列的研究，经过不断发展形成了完备的理论体系，并对加上执行装置的压气机系统进行了建模.除此之外，其他学者[12-15]对于MG模型的拓展和应用均取得了良好成果.

在关于退失速的文献中，很少涉及不同退喘开阀速度的效果及其给整个压缩系统带来的影响.因此，本文以某单级轴流低速压气机为原型，将以压力平衡方程、质量守恒方程及转子动态方程为基础的MG模型仿真和以RANS方程为基础进行三维流场求解这两种数值模拟方法相结合，针对退喘阀控制对压气机性能的影响这一问题展开研究，并具体分析了退喘阀以不同速度开阀对退失速这一过程的影响及其机理.

1 研究对象和研究方法

1.1 研究对象

研究对象以某单级压气机为原型，试验台如图1所示.压气机设计转速为 3 000 r/min，设计流量为6.8 kg/s，轮毂比为0.75，有46片动叶和44片静叶.退喘阀为快速响应气动球阀，排气节流阀为蝶阀.详细设计参数见表1.

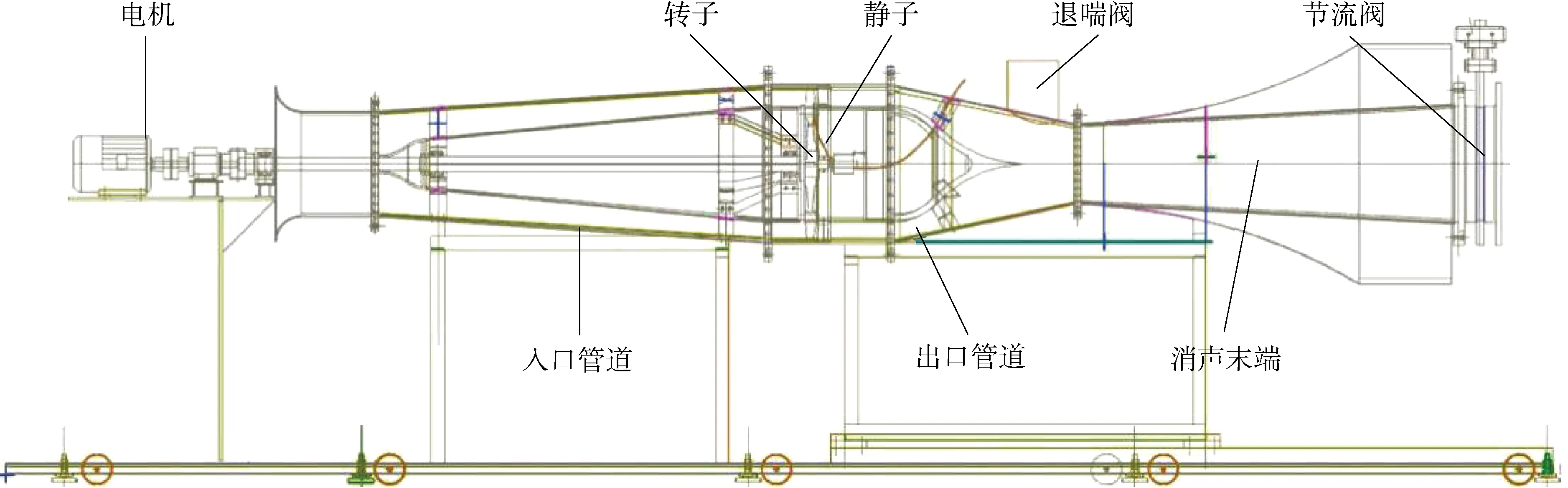
图1 单级压气机系统结构图Fig.1 Structure diagram of single stage compressor system

表1 压气机参数Tab.1 Parameters of compressor

1.2 基于MG模型的数值仿真

为了衡量压缩系统的不稳定工况表现形式，通过压气机转速、当地声速、稳压室容积、平均截面面积、压气机及前后管道总长求得B参数，其定义为

(1)

式中：U为压气机转速；as为当地声速；Vp为稳压室容积；Ac为平均截面面积；Lc为压气机及前后管道总长度.

以B参数为核心的经典MG模型主要含有3个常微分方程，见文献[7].变转速分布式MG模型在原有MG模型对动态过程求解总压平衡方程、质量守恒方程的基础上，添加转子动态方程并将转速变化代入到各个方程中.并且使用傅里叶级数对原本作周向平均的流量进行分解，使其结果精度增加并能表示扰动在周向的传播情况，其矩阵形式为

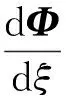
(2)

(3)

(4)

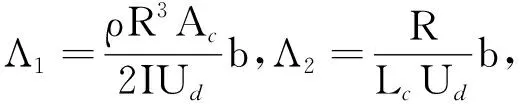
本文在测量试验台尺寸后，选取压缩系统参数如表2.

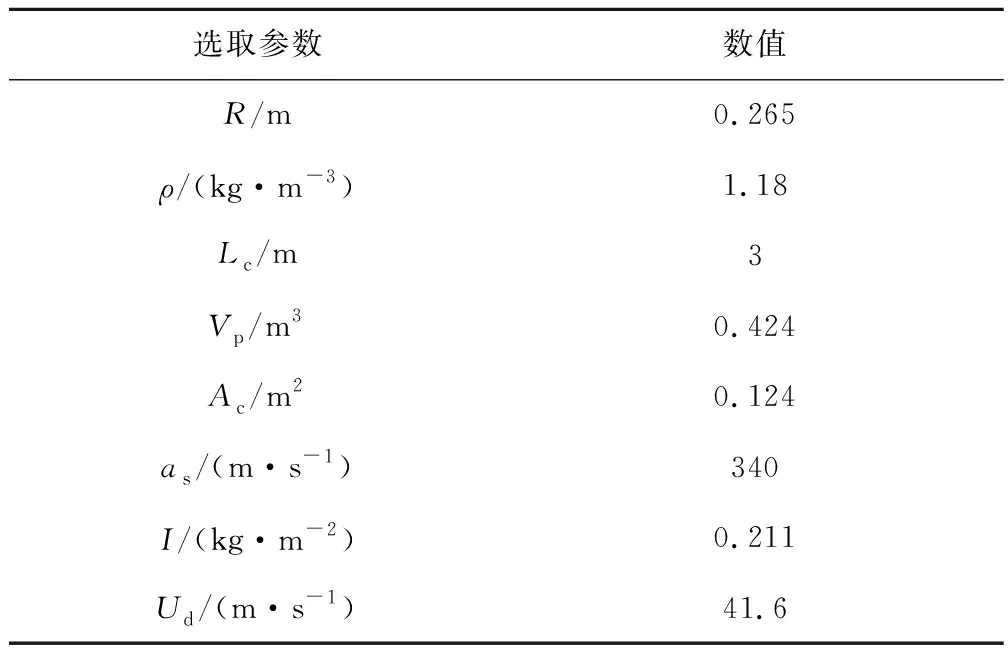
表2 压缩系统参数Tab.2 Parameters of compression system

其中，求解方程需事先给定压气机稳态特性曲线.本文中通过稳态数值模拟求得稳态性能，代入轴对称性能曲线，压气机压升系数Ψc和流量系数Φ的关系如下式：

Ψc=Ψc0+

(5)

式中：Ψc0、H及W分别为轴对称性能曲线参数，通过拟合求解得到Ψc0、H及W分别为 0.185 4、0.153 2 及 0.104 3.

1.3 基于RANS方程的数值仿真

RANS方程的求解主要基于CFX计算平台，计算域及网格划分如图2所示.入口边界距动叶前缘为1.5倍动叶叶尖弦长，退喘阀中心距静叶尾缘为2.5倍静叶叶尖弦长，出口边界距静叶尾缘为3.5倍静叶叶尖弦长，分别在叶片和退喘阀门周围进行加密.入口边界条件给定总压和总温.下游退喘阀门边界条件用质量流量控制，出口边界条件采用径向平衡方程，并且为了使双出口管道系统能够耦合并符合真实情况，使用节流阀模型确定中径处静压：

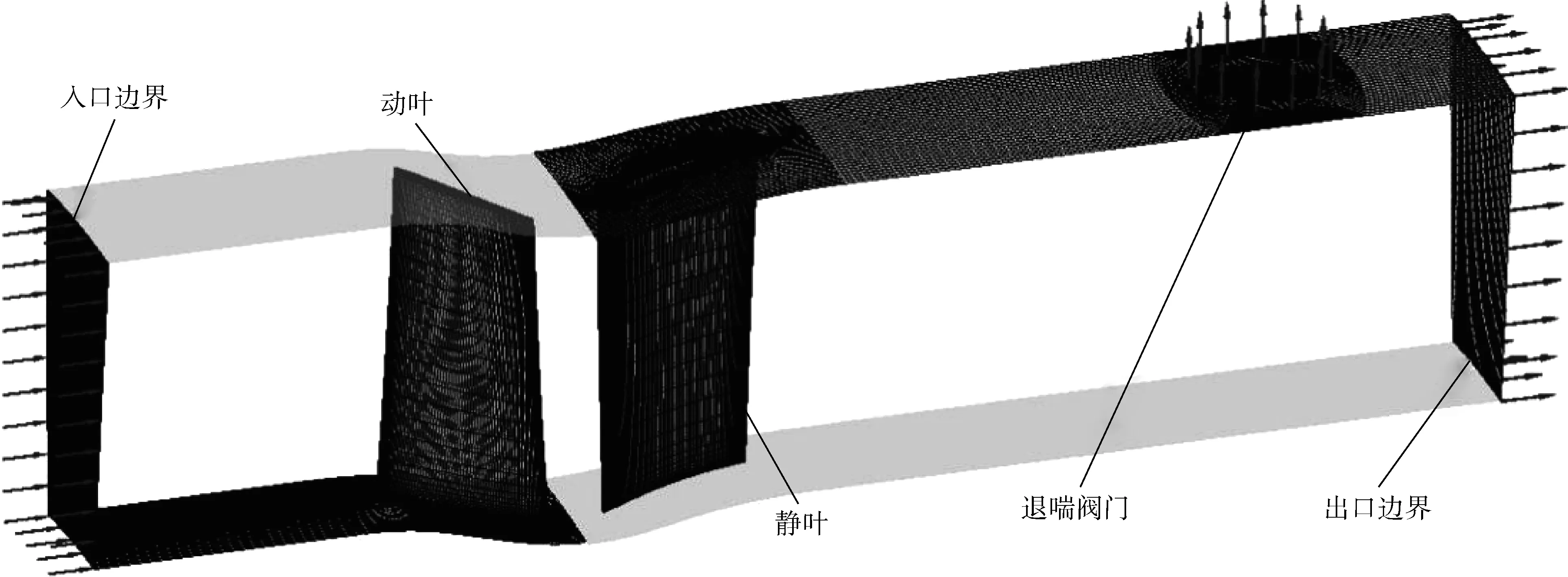
图2 网格划分示意图Fig.2 Diagram of grid generation

(6)

式中：p0为大气压力；ρE为出口截面气流平均密度；UEe为垂直出口气流速度；γJ为节流阀开度系数.动静交界面稳态计算时使用冻结转子法，瞬态计算时使用瞬态转子定子法.叶片、机匣及轮毂壁面均为绝热无滑移壁面.

网格无关性检测时，分别使用网格量N为 7×104、1.6×105、2.1×105及3×105的单通道模型.图3为使用各模型进行稳态计算得到的无量纲性能曲线，综合考虑计算的准确度与耗时后，最终取1.6×105网格.对比k-ε、k-ω和切应力传输(Shear Stress Transport，SST)不同湍流模型和实验结果，如图4所示.可见，实验结果和k-ε及SST均较为接近，且近失速时更接近SST模型，故选取SST湍流模型求解RANS方程.时间步长为3.95×10-5s，相当于每个动叶通道分为11个时间步.

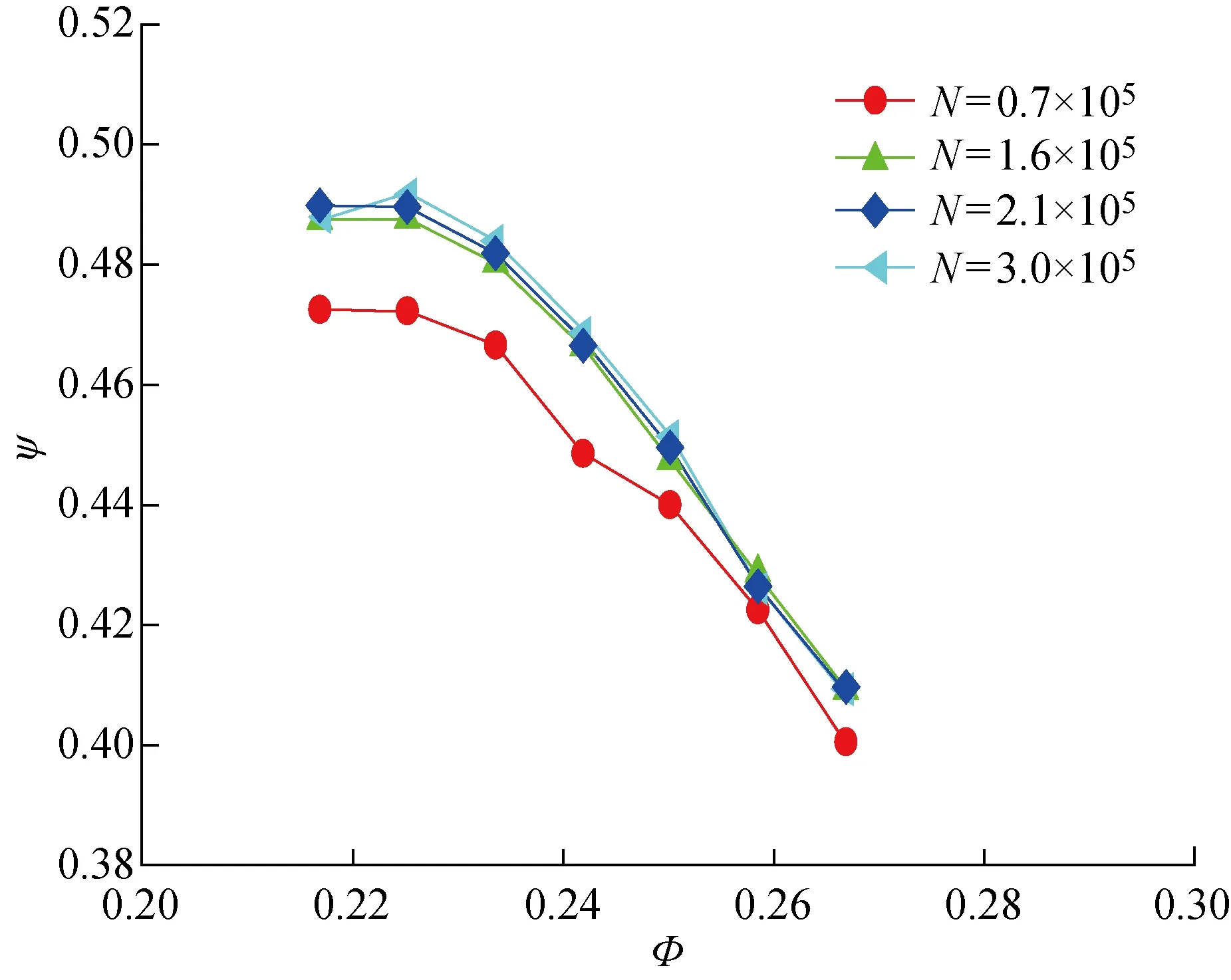
图3 网格无关性检测Fig.3 Detection of grid independence

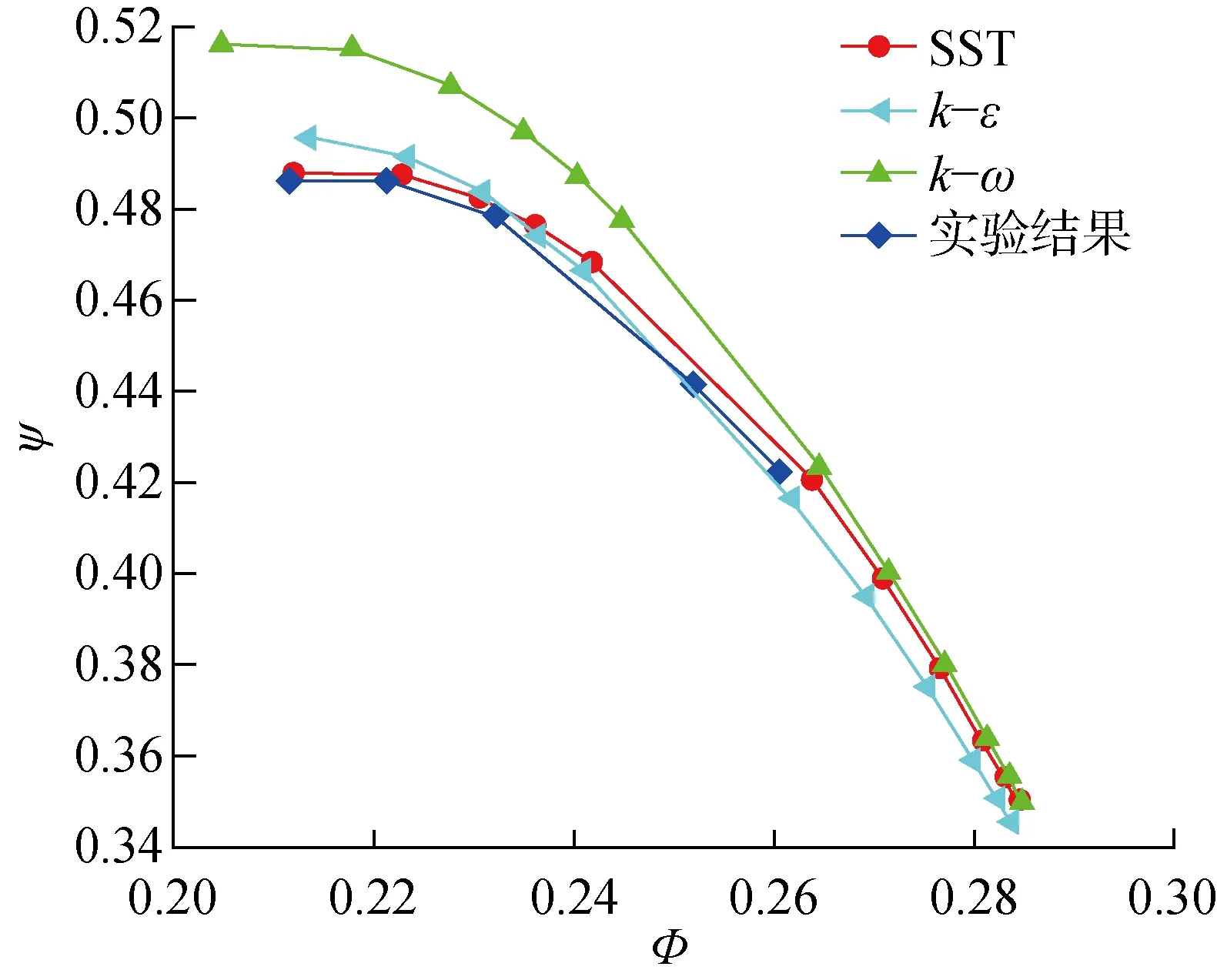
图4 湍流模型验证Fig.4 Verification of turbulence model

2 结果分析

2.1 不同开阀速度性能对比

MG模型在失速前一段任何一个工况作为初场，总会由于“惯性”而先发展至失速曲线，再进行退失速.故为了保证MG模型初场的稳定，将失速充分发展至回流曲线.CFX软件计算由稳态计算的某一失速工况点开始，转为同工况的瞬态计算并经过两转使流场得到一定的发展，以此为统一初场开始退失速.

退失速过程中，数值模拟保持节流阀开度不变，设定退喘阀流量在不同时间内线性增加到同一目标流量0.091 kg/s来表示不同的开阀速度.此目标流量换算成全周时退喘阀流量为0.15 kg/s，压气机出口流量约为0.28 kg/s，选取此流量能够使压气机退出失速.在MG模型中对应目标开度为0.45，分别取开阀速度系数C=1、10、20、+∞(瞬开)，则退喘阀门开度γT可表示为

γT=0.2+0.25γ(CΔt)

(7)

式中：γ(x)为线性开阀函数，满足γ(x)=x，x∈[0,1]；Δt为开阀时间.

2.1.1开阀速度系数C=1 图5中给出了阀门以C=1时开启的退失速性能曲线，图中MG线表示MG模型周向平均后的动态结果，由黑色向红色渐变代表进失速到退失速的发展过程；RANS线为CFX瞬态计算得到的压气机流量系数及压比系数的动态发展结果，由蓝色向粉色渐变代表退失速的发展过程.V1、V2分别为进失速阀门曲线和退失速阀门曲线，并取刚开阀门时的工况点A进行流场分析.

刚开阀门时，RANS线并未像MG线一样逐渐增大流量，而是向流量减少的方向发展.这是因为顶部低速流体流向出口边界受阻，在节流阀和退喘阀整体开度不足以退出失速时，会在靠近出口机匣处形成大范围回流，这种回流进一步堵塞了出口流场，而使压气机发展至更严重的失速工况.图6为开阀后经过0.4转时截取的瞬时流线图像，图中v为速度，对应图5性能曲线的A点.

图6 工况点A的回流流场堵塞状况Fig.6 Blockage of reflux flow field at operation point A

迟滞回线可以分为4个部分：压气机稳态特性曲线、从稳定工况节流进入失速的进失速阀门曲线、开阀后仍处在不稳定状态的失速曲线和以迟滞形态退出失速的退失速阀门曲线.图5中MG线形成明显的迟滞环，在刚开始退失速时，工况逐渐沿着回流的曲线折返，然后经过失速曲线，接着在退失速阀门曲线上有较高的压升，最终进入稳定特性线后沿着特性线逐渐增大流量.其中，进入失速和退出失速的过程相较更快，其阀门曲线可以用流量系数的二次函数表示，如图5中V1和V2，其函数ΨV1、ΨV2分别为

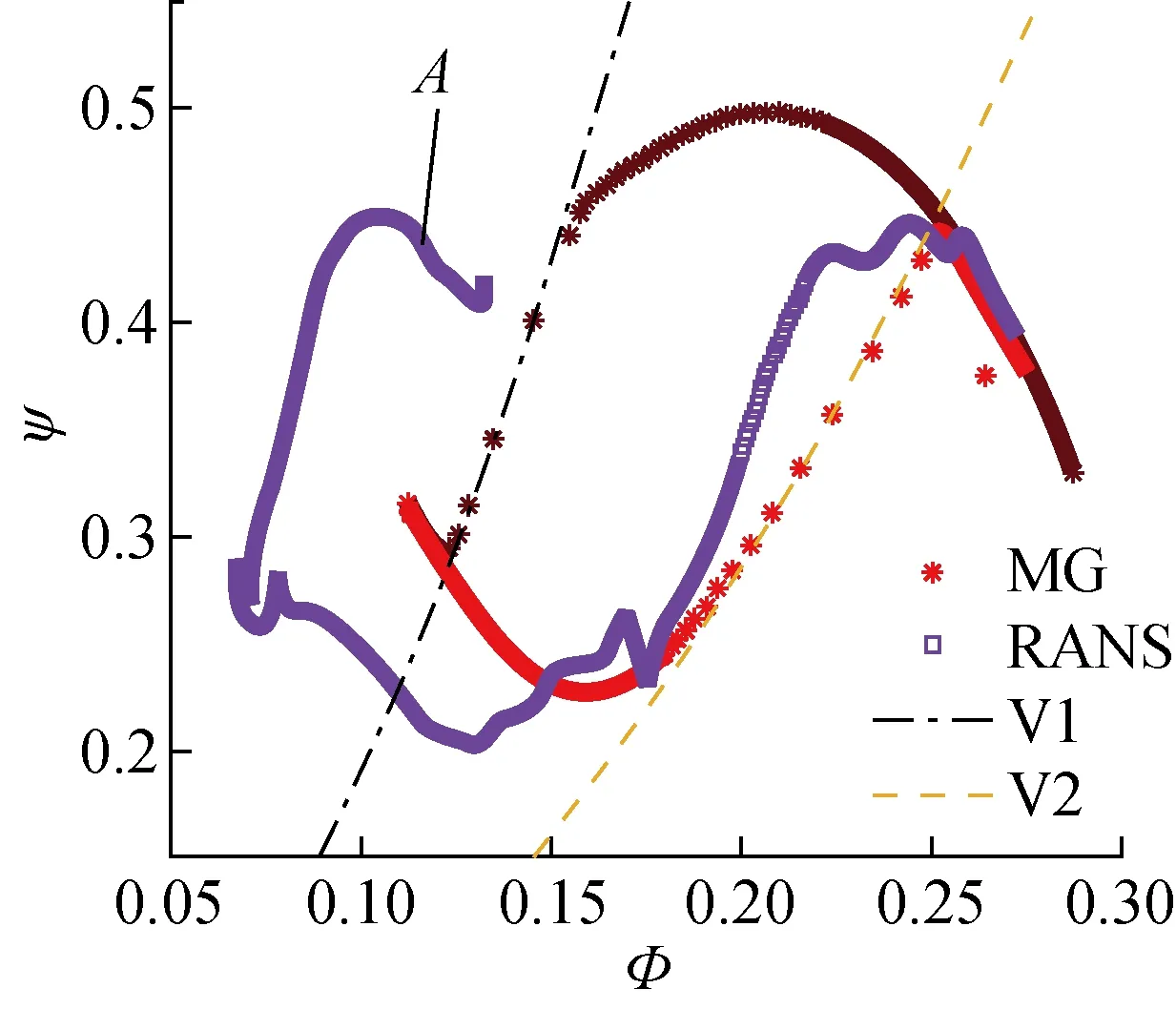
图5 C=1时退失速性能Fig.5 Stall recovery performance at C=1

ΨV1=18.88Φ2

(8)

ΨV2=7.113Φ2

(9)

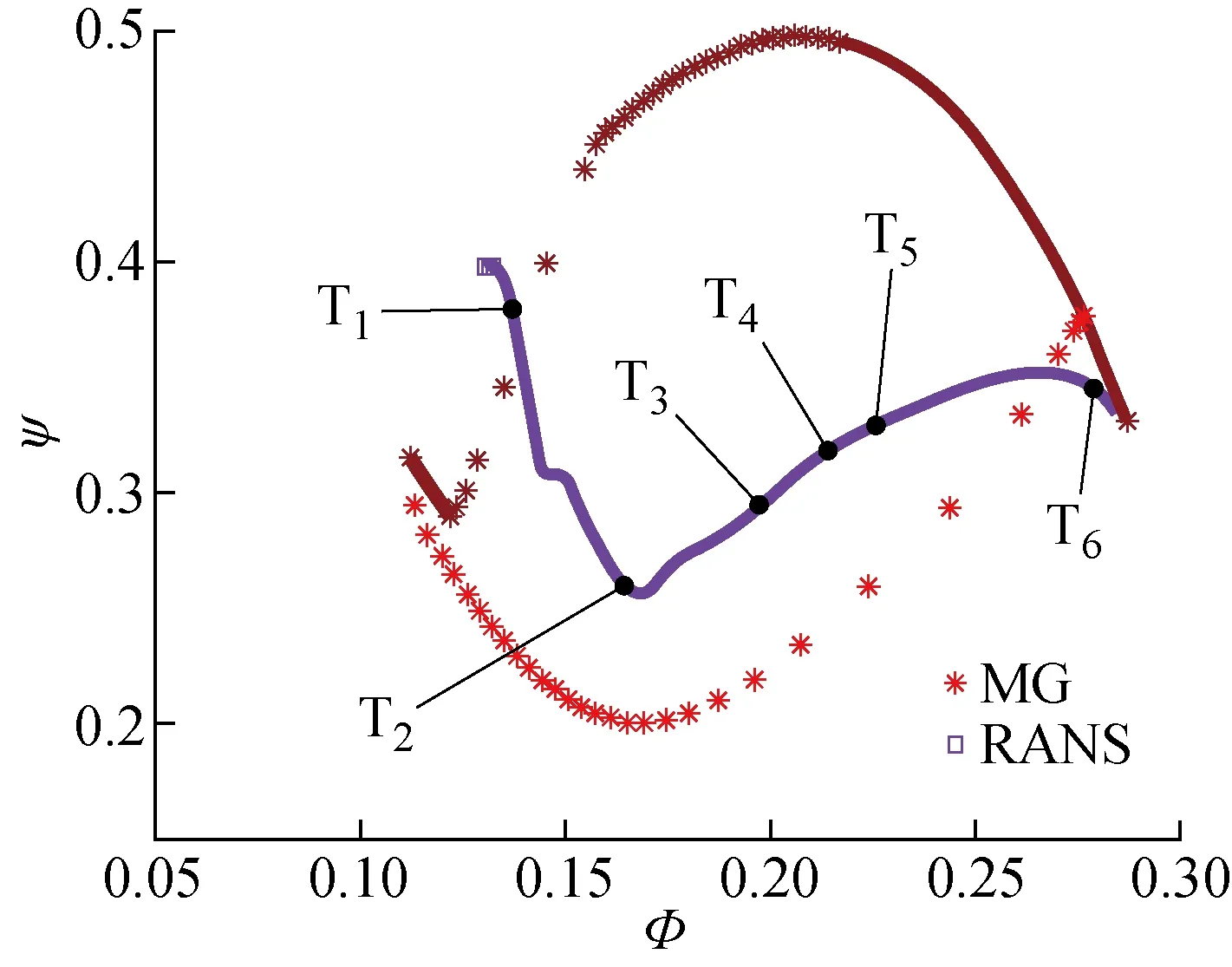
图7 C=10时退失速性能Fig.7 Stall recovery performance at C=10

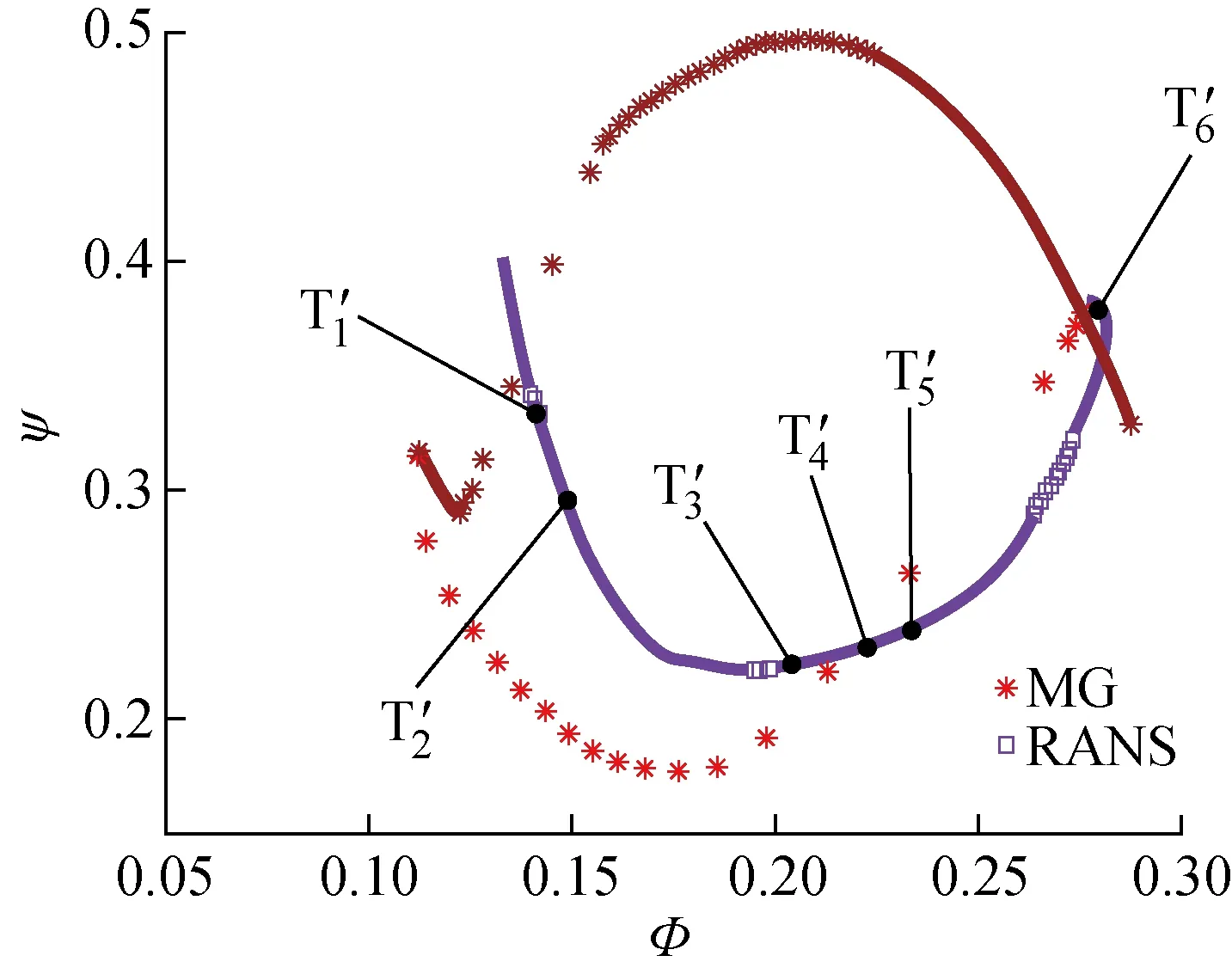
图8 C=20时退失速性能Fig.8 Stall recovery performance at C=20

图9 C=+∞时退失速性能Fig.9 Stall recovery performance at C=+∞

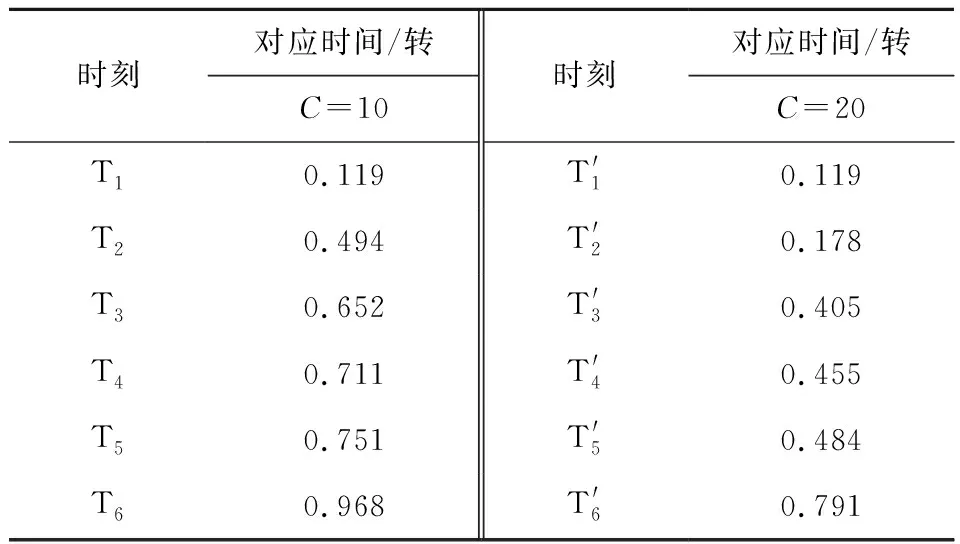
表3 瞬时云图对应时刻Tab.3 Corresponding time of instantaneous contours

对比3个工况的MG线，开阀速度越快，开阀瞬间的压降越大，相应退失速过程最大压降越大.在瞬开阀门的极端情况中，不再有失速曲线，而是直接跳跃至退失速阀门曲线.

3个工况时均处理后的RANS线与MG线趋势均大致相同，说明CFX中的前处理及参数设置基本准确.不过在阀门曲线段，RANS线逐渐由凸曲线变凹曲线，这是因为阀门开启速度越快，退失速过程的压力均值越低，且随着开阀速度的进一步加快，其降低程度更大.

下文着重对比C=10和瞬开两种方式开阀时，退失速过程中细节性能参数的变化.如图10、11分别为分布式MG模型中以不同速度开阀，流量接近平稳时周向当地流量的变化情况，其中θ1=0°、θ2=120°、θ3=240° 分别为周向均布的3个测点的位置，τ为时刻.由分布式MG模型结果可以看出，随着开阀速度的加快，流量信号稳定所需时间缩短，同时其波动幅度增大，不过其波动仍近似规则的正弦形状.对比扰动的周向传播速度，即图10、11中斜线，可见两者斜率大致相同，表示退失速时扰动的周向传播速度并不随开阀速度而发生改变，这与文献[4]中退失速会加快扰动周向传播速度的结果有所不同，产生差异的原因在下文解释.

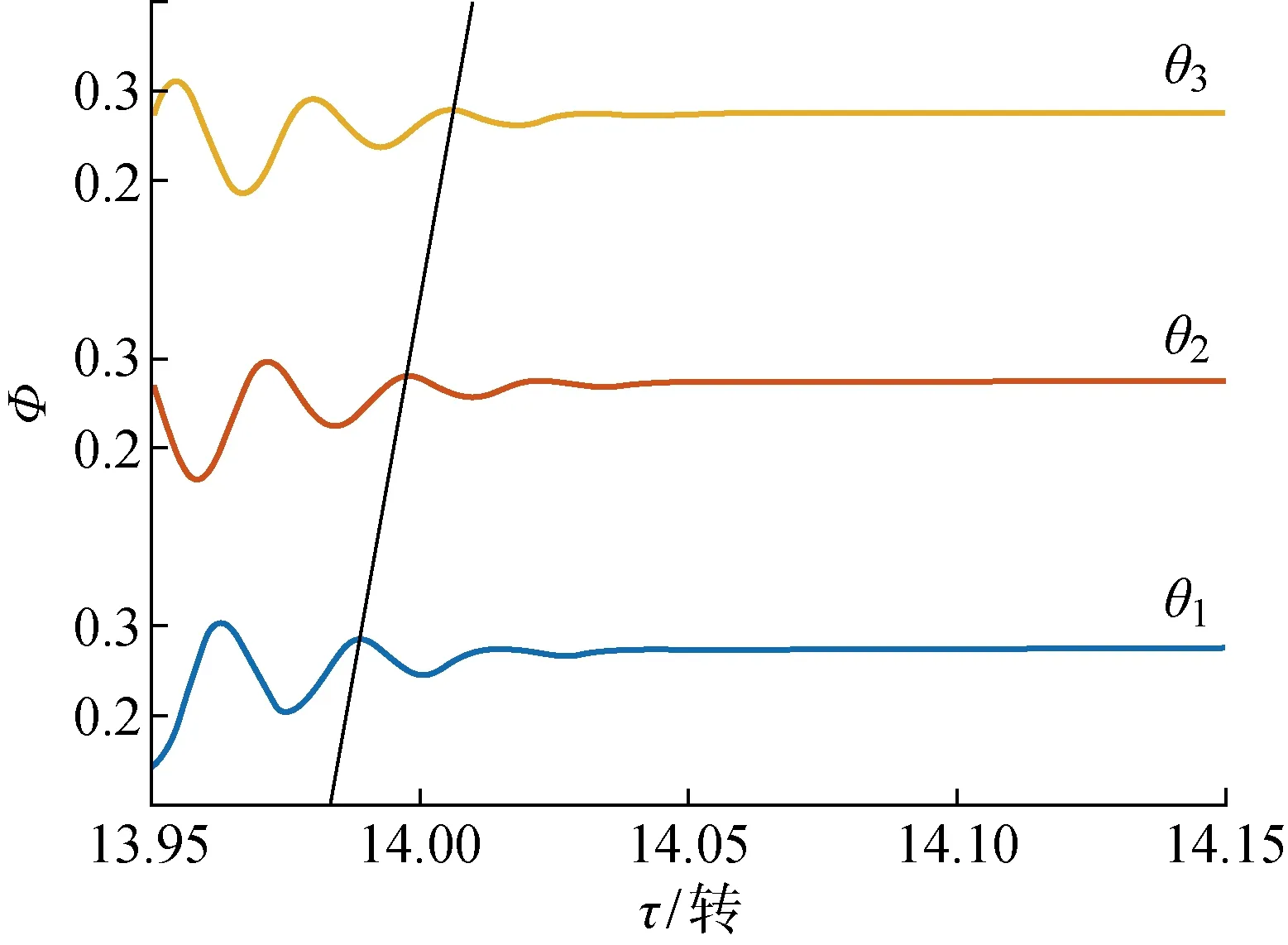
图10 C=10，接近稳定时当地流量Fig.10 Local flow rate at C=10 near steady condition

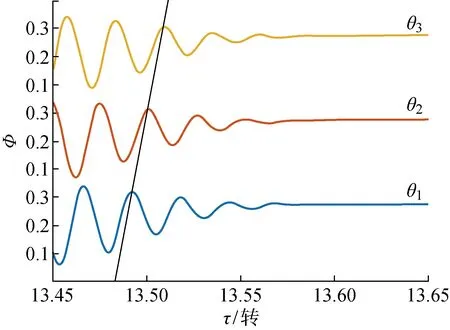
图11 C=+∞,接近稳定时当地流量Fig.11 Local flow rate at C=+∞ near steady condition

数值模拟中，分别在级后的叶尖、叶中及叶根部位设置测点，观察各设置工况中测点压力随阀门开启的变化情况，如图12所示，图中ps为静压.对比径向3个区域，可知瞬间开阀时在径向各部位均引起了强烈的压力波动.以速度系数为10和20进行开阀，则主要在叶尖及叶中产生波动.以不同速度开阀时，叶尖的压力变化总是相对于叶根较为剧烈.这是因为动静叶区域失速的流场同图6，堵塞主要发生在叶尖区域，而叶根区域流动较顺畅，则退失速时压力波动也呈现出由叶根到叶尖逐渐增强的趋势.

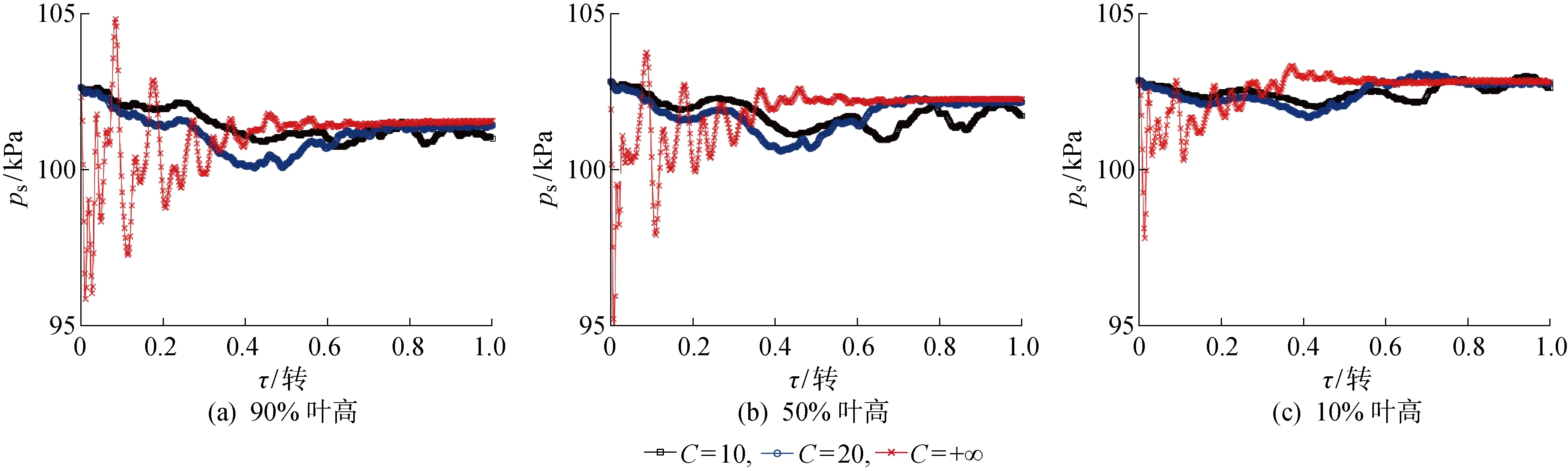
图12 级后测点压力变化Fig.12 Pressure changes at point after the stage

2.2 不同开阀速度退失速过程流场分析

2.2.1C=10时退失速过程流场分析 由于堵塞和最明显变化的区域均为叶尖区域，现提取C=10时，失速过程中几个关键时刻，90%叶高处云图和流线图进行流场分析，如图13所示，瞬时截取的云图即为 2.1.2 中C=10时的6个工况.T1时刻代表了T1～T2时段的失速流场的基本特征：级前后压差很低，叶顶流场基本堵塞.另外，通过将低压区和流线图相对照，即图13的T2时刻和图14，可以发现低压区和堵塞流场的前端位置相对应.T2时刻漩涡向下游迁移，与低压区位置不再对应.

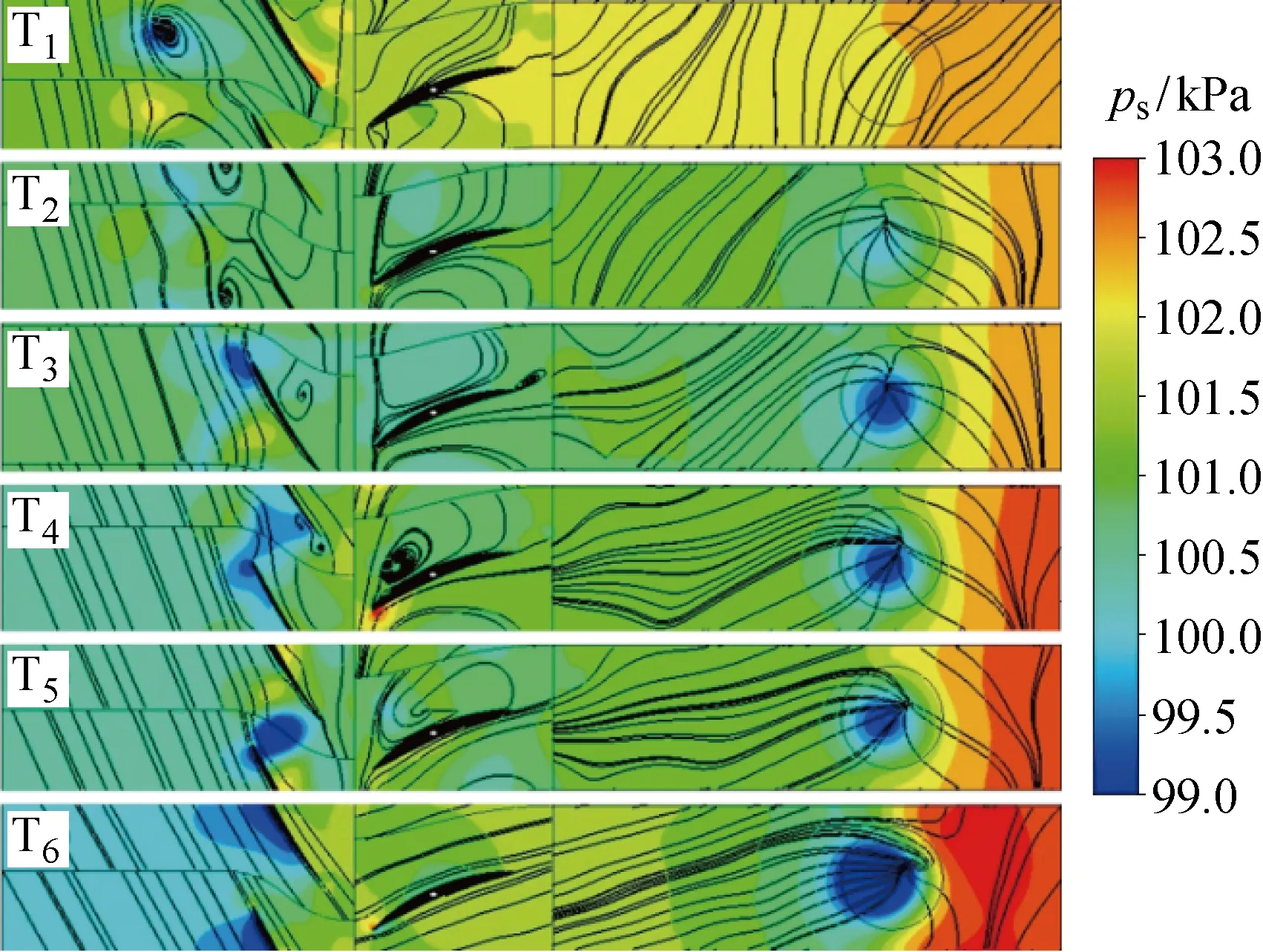
图13 C=10退失速流场变化Fig.13 Flow changes in stall recovery at C=10

图14 C=10，T2时刻流线图Fig.14 Diagram of streamline of T2 at C=10

对于低压区，T2～T3时段低压区逐渐向下游移动并最终抵达叶片前缘.T3～T4时段，低压区在依附于动叶吸力面前缘后，一方面由于动叶的转动效应在周向拉伸，另一方面又被轴向流动的高速气流拖拽沿吸力面从前缘移至中部.同时高速气流的冲击作用使低压区的一部分分离，分离的小低压团向下游迁移并逐渐消散，这个过程使得低压区被削弱，接着从压力面由前缘溢流至吸力面，形成一个周期.在T4～T5时段，被减弱的低压区再次经过这样一个周期过程.之后低压区由压力面过渡到吸力面，形成新的吸力面低压区，新的低压区充分发展后，保持稳定，此时动叶区域已经基本流通.在T6时刻，静叶及出口管道扰动消散后流场稳定变化，退失速过程完成.

为了验证由MG模型中得出的退失速过程扰动周向转递速度不变的结论，现对比失速团两次经过动叶流道的时间间隔，T3与T4时段的间隔时间为0.059转，T4与T5的间隔时间为0.04转，可发现第2次经过动叶流道时时间更少.现针对文献[4]的结论，结合流场分析结果给出如下解释：低压区在受到周向高速气流的冲击作用被分离一部分后，其强度被削弱，并因此在周向加速，更接近转子旋转速度.在文献[7]的分布式MG模型中，即使将扰动进行周向傅里叶变换，其本质还是一个入口扰动，并未涉及到扰动在动叶流道内的损失过程，故而未能模拟出这种现象.

2.2.2C=10，20退失速过程流场变化对比 在C=20时退失速流场静压云图中，取对应图13中流场特征的时刻进行对比分析，如图15，瞬时截取的云图即为 2.1.2 中C=20时的6个工况.整体上看，C=10与C=20两者低压区和漩涡的运动规律基本一致.

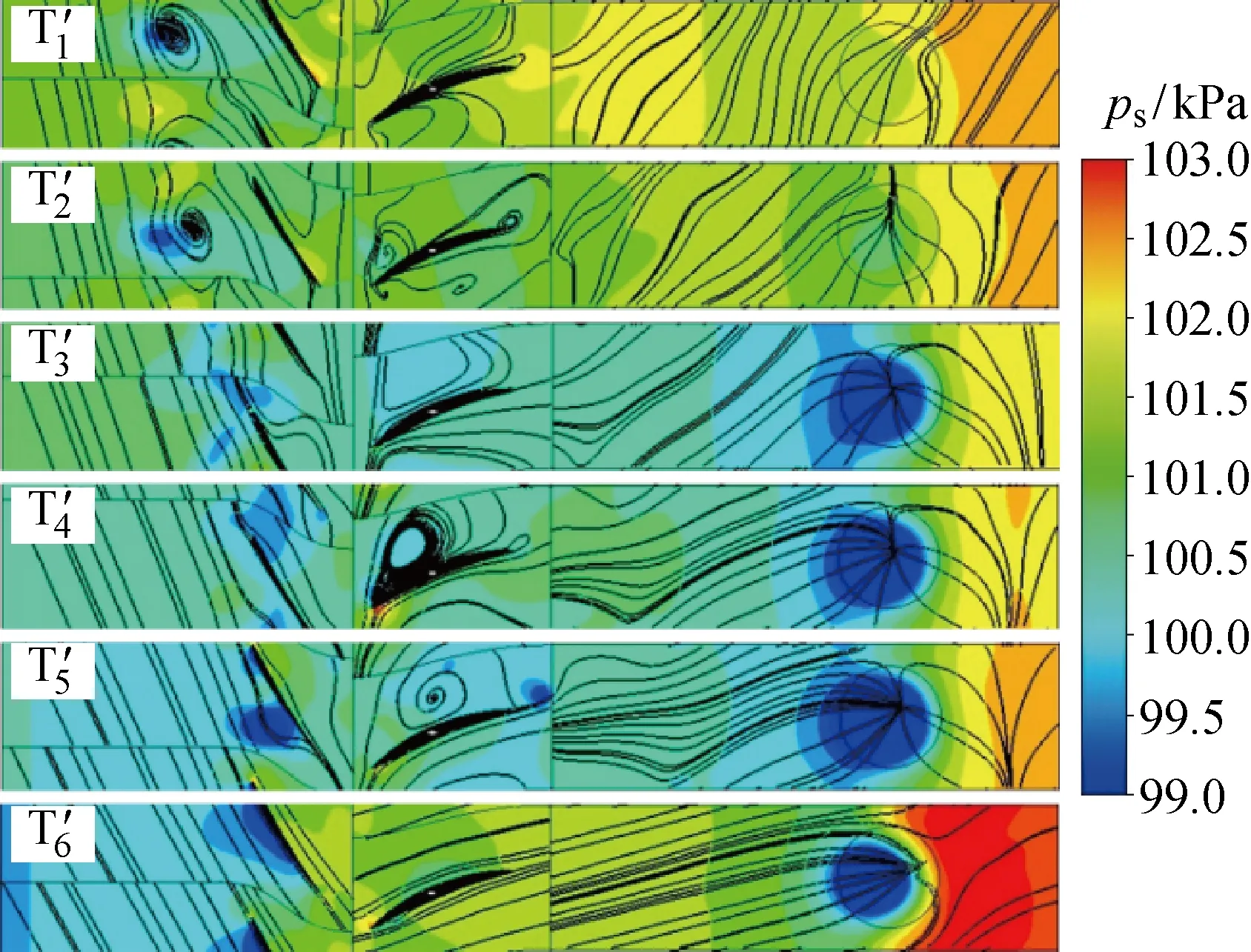
图15 C=20退失速流场变化Fig.15 Flow changes in stall recovery at C=20

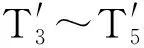
3 结论

本文针对退失速时的退喘阀门不同控制方式的效果进行了研究，主要结论如下：

(1)将MG模型和CFD软件这两种数值模拟方法相结合，以MG模型验证CFD计算的前处理和参数设置的准确度，以CFD软件对MG模型流场细节的欠缺作补充.总体来看，两者对退失速性能预测的趋势基本一致.

(2)在较为缓慢开阀工况中，刚开阀门时其开度过小，不仅不利于退出失速，在某些情况下产生下游至退喘阀的回流，会进一步堵塞流场，使压气机性能更加恶化.

(3)文中选取了一个能使压气机退出失速的目标流量，主要比较了不同开阀速度对压气机性能的影响.对于文中存在迟滞回线的压气机系统，开阀速度越慢，在迟滞回线上停留的时间越长，退失速所需时间越长.开阀速度越慢，产生的流场波动就越大.

(4)对于分布式MG模型的预测结果，以不同的速度开启退喘阀，退失速过程流量扰动周向转递速度不变，说明退失速过程在本质上是相同的.CFD数值模拟的结果也证实了这一结论，并另外比较了不同开阀速度时流场的变化.开阀速度越快，扰动受轴向高速气流削弱程度越大，致使其周向传递速度加快而更接近转子转动速度.