加强联系,沟通算理与算法
陈瑞华
【摘 要】“竖式”本质上是记录运算过程的一种工具,它在小学数学运算中有着重要的作用。通过横式记录与竖式记录方式的对比,能帮助学生沟通横式计算与竖式计算的联系,让学生充分理解用竖式计算“除数是整数的小数除法”的算理,掌握相应的算法,感受竖式计算的简洁性和实用性。
【关键词】小数除法;算理;算法;竖式计算
“竖式”与“横式”一样,能反映数学运算的过程,体现数学运算的算理。本质上它是记录运算过程的一种工具,在小学数学运算中有着重要的作用。在小数除法的计算中,利用竖式帮助记录会让计算过程更加清晰直观。
基于学习路径分析的“小数除法”单元的核心课时可以确定为以下三节:基于算理理解的“小数除法”活动课,“除数是整数的小数除法”以及“除数是小数的小数除法”。
“除数是整数的小数除法”是小数除法单元教学的基础,它的算理根据整数除法的算理迁移而来,本质是对计数单位的细分。在实际教学中,教师根据单元教学的分析与设计,把原教材中“小数除以整数(被除数无须补0)”“整数除以整数”两课时的内容合并为一课时。通过在实际情境中解决问题,沟通横式计算与竖式计算的联系,让学生理解除数是整数的小数除法的算理,掌握算法,体会竖式计算的作用和价值。
【教学过程】
(一)理解算理,感受竖式计算的简洁性
1.复习回顾,引入竖式
师:还记得活动课上的任务一吗?(教师出示任务一,略)11.5元钱是怎么分给5个小伙伴的?哪位同学能跟大家分享一下换和分的过程?
学生描述“分一分”活动的过程。
师:会列竖式计算吗?我们一起来试一试。请看活动要求。
教师出示活动要求。
(1)想一想,算一算:观察活动课上的横式记录,想一想如何用竖式把分的过程记录下来,尝试独立用竖式计算本题。
(2)说一说,议一议:在小组中说一说竖式计算的过程,同桌之间互相交流竖式计算中每一步的意思、与横式的联系。
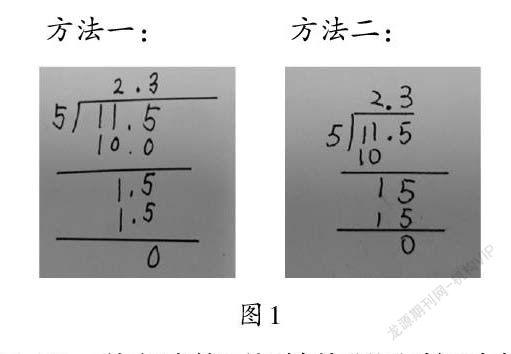
(3)反馈与分享:教师呈现学生的竖式记录方法(如图1),并引导交流。
方法一: 方法二:
师:哪一种方法能更好地体现活动课中换钱和分钱的过程?
生:方法一中,1.5[÷]5没有体现换钱的过程,还是1元和5角,合并成1.5元,没有换呀。
生:15[÷]5体现了把1元换成10角,和5角合并成15角,再平均分给5人,每人分得3角。这种方法更合适。
2.对比沟通,体会简洁
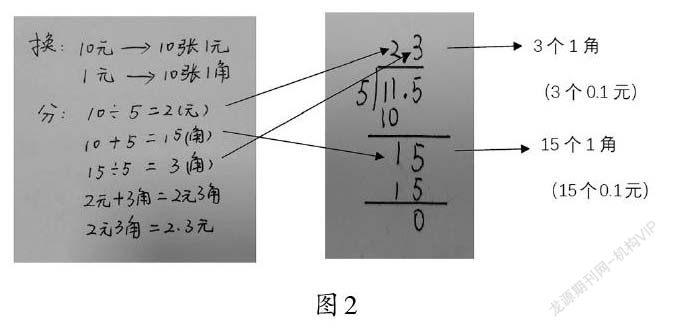
师:让我们一起来梳理一下竖式计算的过程(如图2)。
师:同学们,分的过程既可以用横式记录,也可以用竖式记录,哪一种方法更简单、更实用?
生:我认为用横式记录比较清楚,我可以看清每一次分钱的过程。
生:我认为用竖式计算更加简单,竖式的步骤比较少,每一步也体现了分钱的过程。
生:我认为竖式计算比较通用,它的计算过程很容易掌握,而且计算又快又准确。
师:横式计算和竖式计算都记录了除的过程,竖式计算可以用固定的、程序化的步骤记录运算步骤,是解决相应计算问题的一种“通法”,它更加简洁。
学生在完成这个学习任务的过程中,通过联系换钱和分钱的过程,对比横式与竖式,明白15[÷]5就是15個0.1元除以5,得到3个0.1元,初步理解算理。借助交流对比,感受竖式计算的简洁性。
(二)掌握算法,体验竖式计算的实用性
师:活动课上的任务二,你们能尝试自己列竖式计算吗?(教师出示任务二,略)一起来试一试。请大家看活动要求。
教师出示活动要求。
(1)算一算:请独立列竖式计算。
(2)说一说:在小组中说一说竖式中每一步表示的意思。
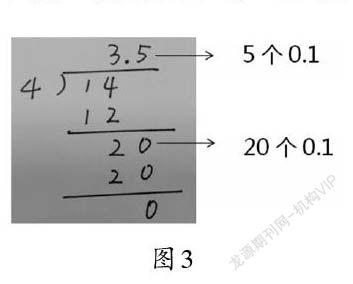
学生在活动后进行全班交流,教师呈现学生解决问题的方法(如图3)。
师:请你说说看,你列的竖式,每一步分别表示什么意思。
生:我先用14除以4,表示每根跳绳可以平均分到的长度是3米。这时还剩下2米,我在2后面加上了0,表示2米换成20分米,再继续除得到商5,就是说每根跳绳可以再分到5分米。所以平均每根跳绳长3.5米。
教师随着学生的回答,梳理横式和竖式的对比过程(如图4)。
师:这一问题和刚刚解决的分钱问题有什么不同?
生:这一题的被除数和除数都是整数。
生:除完后整数部分不够除,就要补0再除。
师:当被除数分完后还有余数时,需要补0继续除;这个0补完后,被除数在这里表示什么?
生:20分米,也就是20个0.1米,商就是5个0.1米。
师:同学们,今天我们分别学习了用横式和竖式来记录小数除法除的过程,这两种方法有什么联系?
生:都可以记录分的过程。
生:都可以得到正确的结果,但我觉得竖式计算的方法更实用。
生:我也觉得竖式计算更实用,不容易错。
师:正像同学们说的这样,我们在平时的计算中大多用竖式计算的方法进行小数除法的计算,在计算的过程中我们要知道先分什么,再分什么,当不够分的时候要补0继续分,看来用竖式计算的方法更加实用。
通过师生互动、生生互动,学生理解了“如果整数除以整数后还有余数,那么可以在余数后补0继续除”的道理。通过横式与竖式的比较,体验竖式计算的实用性。
【教学思考】
数学运算在过程的思考性与思路的灵活性上做“加法”,可以更好地实现通过运算促进数学思维发展的目标,真正体现数学运算素养的教育价值[1]。《义务教育数学课程标准(2011年版)》指出,“在基本技能的教学中,不仅要使学生掌握技能操作的程序和步骤,还要使学生理解程序和步骤的道理”。本节课的教学,不仅要让学生掌握除数是整数的小数除法的算法,更要让学生明白为什么这么算,理解每一步计算的道理。学生在计算小数除法时,不仅要掌握竖式的程序性操作方法,更要明白这样做的道理。抓住横式计算与竖式计算之间每个步骤的对应关系,在横式记录和竖式记录之间架起对应的桥梁,可以充分展示小数除法竖式计算的过程,让学生真正理解除数是整数的小数除法的算理,掌握算法,感受竖式计算的简洁性和实用性,体验竖式计算的作用和价值。
参考文献:
[1]姜荣富.数学运算:算法化与思考性[J].小学数学教师,2021(1):57-62.
(广东省深圳市宝安区宝安小学 518100)

