凸显转化，促进算理理解与算法掌握

吴玉兰

【摘   要】“除数是小数的小数除法”是小数除法单元学习的难点，理解算理的关键在于体会转化思想，其实质是被除数和除数同步转化后的计数单位细分。基于学习路径分析进行单元整体教学时，可以借助单位换算、运算律、直观图等方式，理解被除数和除数的同步转化，并能在理解算理的基础上抽象出竖式计算方法。

【关键词】小数除法;转化;理解算理;竖式算法

基于学习路径分析，“除数是小数的小数除法”是“小数单元”核心课时中的最后一课时。从对学生的前期调查中可见，会用竖式计算“除数是小数的小数除法”并能解释算理的学生占比很少。可见，“除数是小数的小数除法”是本单元学习的难点。

在本单元前两节课“小数除法”活动课以及“除数是整数的小数除法”的学习过程中，学生经历了计数单位细分的活动过程，并能在横式、竖式的联结中理解了“除数是整数的小数除法”的算理，掌握了竖式算法。这为本节课的算理理解与算法掌握奠定了良好的基础。因此，本节课可以继续以“元、角、分”为模型，以问题解决多样化为载体，凸显转化的必要性与可能性，在转化的背景下理解“除数是小数的小数除法”的算理，并抽象出相应的竖式计算方法。

【教学过程】

（一）情境引入，提出问题

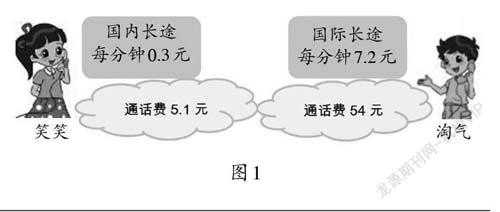
师：月底到了，笑笑和淘气分别收到了移动公司的一条短信（如图1）。你们觉得谁打电话的时间长一些？

生：我觉得淘气打电话的时间长，因为他的通话费比笑笑多很多。

生：我觉得不一定，淘气虽然通话费多，但他每一分钟的钱也比笑笑多很多。

师：到底谁打电话的时间长呢？接下来我们一起来解决。

（评析：本单元的前两节核心课，都创设了分钱的情境，借助人民币的转化来解释说理。因此，本课仍创设与人民币相关的实际情境，为学生的解释说理创设条件。）

（二）理解算理，探究算法

教师出示学习任务一：国内长途每分钟0.3元，笑笑付了5.1元通话费。求笑笑打电话的时长。

1.自主探究，解決问题

教师出示活动要求：想一想，可以怎样算？写一写你的方法（有几种写几种）。

学生独立思考解决问题。

2.分享交流，体会转化

（1）同桌交流：向同桌介绍你的方法，想一想不同的方法之间有没有相同的地方。

（2）全班交流：谁愿意与大家来分享你的方法？

生：把元化成角，5.1元=51角，0.3元=3角，51[÷]3=17（分）。

师：还有谁也用了这样的方法？你为什么要把元转化成角？

生：因为用元作单位计算时是小数除以小数，不会算;用角作单位就变成了整数除以整数，很好算。

师：简单的一步单位换算，就把不会的转化为会的，这种方法真好！有不一样的方法吗？

生：我是用商不变性质来想的。根据商不变性质，把5.1和0.3同时乘10，5.1[÷]0.3=（5.1[×]10）[÷]（0.3[×]10）=51[÷]3=17（分），这样也能得到笑笑打了17分钟电话。

师：为什么要把被除数和除数同时乘10，而不是乘2或者乘3？

生：因为同时乘10后就能把小数除法变成整数除法。

师：观察这两种方法，有没有相同的地方？

生：都把除数是小数的除法变成了除数是整数的除法。

生：都把不会的变成会的。

师：是的，无论是单位换算，还是用商不变性质，都是把没有学过的“除数是小数的除法”转化成“除数是整数的除法”，用旧知识解决了新问题。

3.诠释转化，理解算理

（1）数形结合，探究竖式算法。

生：老师，我有个问题，小数除以小数能列竖式计算吗？

师：这是个很好的问题。小数除以小数，能不能列竖式计算呢？能的话竖式又该怎么列呢？我们一起来试一试。

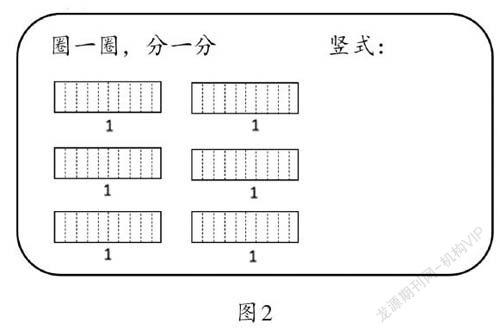
教师出示活动要求：列竖式计算5.1[÷]0.3，想一想，为什么这样列？可以在图（如图2）中圈一圈来说明。

（2）诠释转化，理解竖式算理。

教师展示三幅学生作品（如图3），提问：有什么想问的吗？

生：我们是要算5.1[÷]0.3，但竖式①是在算51[÷]3，这样可以吗？

师：竖式①的主人能解释吗？

生：我觉得可以看这张图（如图4）。我们可以把5.1看成51个0.1，把0.3看成3个0.1，5.1[÷]0.3就是把3个0.1看成一份，算一算51个0.1里有这样的几份，所以也可以用51[÷]3来计算。而且我去圈过了，结果和51[÷]3竖式的得数是一样的。

师：原来他是从小数的意义出发，把5.1和0.3转化成了51个0.1和3个0.1来想。这样列竖式可以吗？

生：可以，但我觉得如果加一步5.1[÷]0.3=51[÷]3，再列这样的竖式会更好。这样我们就能知道为什么列这个竖式了。

生：我想问问竖式②的主人，为什么小数点上要画个“×”？

生：我其实也想把5.1[÷]0.3变成51[÷]3。画个“×”就表示原来的小数点不要了，变成了51[÷]3，再用除数是整数的方法来计算。

师：原来你想让我们更清楚地看出算式转化的过程。能具体说说每一步分别表示什么吗？

生：我们也可以结合图（如图5）来看，把5.1去掉小数点，看成51个0.1;把0.3去掉小数点，看成3个0.1。先拿出30个0.1，每3个0.1为一份圈一圈，正好可以圈成10份，所以竖式的十位上写1;剩下的21个0.1再按每3个0.1为一份圈一圈，可以圈这样的7份，所以竖式的个位上写7，合起来就是17个0.1。

师：你能借助图来解释竖式每一步的意义，真好！

生：我觉得竖式③不大对，因为我们计算整数除法时，要一位一位往下除。他这样列竖式不是一位一位除的，如果被除数和除数大一点，计算复杂一点，这样列竖式就有可能算不出结果。

（其他同学纷纷点头表示同意）

师：你们真会思考，对每一个竖式都提出了自己的看法。现在你觉得哪一个竖式能更清楚地看出我们的思考过程？

生：竖式②，可以清楚地看出把5.1[÷]0.3变成51[÷]3。

（3）对比思考，揭示转化本质。

师：刚才我们用横式、图、竖式解决了笑笑打电话的时长问题。现在请你观察这些方法，有什么发现？

生：它们其实都是把被除数和除数同时乘10，转化成除数是整数的除法。

生：同时乘10后就把几个1变成了几个0.1，这样就把小数除法变成了整数除法，再按照除数是整数的除法去计算就行了。

师：如果变成几个0.1，除数还不是整数呢？比如，除数是0.03。

生：那就变成几个0.01。

师：原来我们把1、0.1这样的计数单位分出更小的计数单位，就能把除数是小数的除法转化为除数是整数的除法了。

（评析：除数是小数的小数除法竖式记录的关键在于体会转化思想，其实质是被除数和除数同步转化后的计数单位细分。因此在本环节中，引导学生用不同的方法解决问题，并通过将单位进行转换，利用商不变性质分析题目，以及借助直观图与竖式进行沟通联系等方式，促进学生理解被除数与除数的同步转化，理解算理，建构竖式的意义。）

（三）练习巩固，拓展提升

教师出示学习任务二：国际长途每分钟7.2元，淘气付了54元通话费。求淘气打电话的时长。

1.提出任务，尝试解决

师：解答了笑笑的打电话时长问题，我们再来帮淘气算一算他打了几分钟的电话。

教师出示活动要求：①列竖式计算淘气的打电话时长;②用其他方法验算;③和同桌说一说为什么可以这样算。

2.方法分享，判斷说理

教师展示两位学生的方法（如图6）：你支持谁？理由是什么？

生：我同意方法②。如果把7.2元看成72角，54元应该看成540角，那么54[÷]7.2应该转化成540[÷]72。方法②是对的，方法①变成了54[÷]72，所以是错的。

师：他结合实际情境，把元转化成角来解释说理，真好！有不同的想法吗？

生：我是把7.2看成72个0.1，54应该变成540个0.1，所以方法②中的竖式才是对的。如果淘气只打了0.75分钟，连1分钟都没到，话费应该连7.2元都没到，怎么可能会有54元话费呢？

生：我还用乘法算过了，7.5[×]7.2=54，所以方法②是对的。

师：你们用不同的方法，说明了方法②的竖式列对了，结果也算对了，那他的计算过程看得懂吗？

生：我们可以这样想，把72个1角看成1份，540角里可以先分出这样的7份，个位上写7;还剩36个1角，正好是72角的一半，也就是有这样的0.5份，所以在十分位上写5，所以最后结果是7.5。

生：我是用整数除法来想的。我们用商不变性质把54[÷]7.2变成了540[÷]72，540里有7个72，个位上写7，分后还剩36，把36再看成360个0.1，除以72后就能得到5个0.1，所以最后结果是7.5。

师：你们不仅能算，还能解释竖式中每一步的意义，真了不起。

（评析：计算54÷7.2与5.1÷0.3的难度是不一样的，后者只需进行被除数和除数的同步转化，再按照整数除法进行计算即可，而前者不但需要进行被除数和除数的同步转化，还需要进行两次补0扩充数位。在第一节“小数除法”活动课和第二节“除数是整数的小数除法”的课的学习中，学生对于在被除数后面补0扩充数位、细化计数单位的做法已有了一定的经验积累，因此在本环节中，放手让学生去尝试，在正误竖式记录的对比辨析中再次理解被除数与除数的同步转化，夯实对计数单位细分的理解，沟通小数除法竖式之间的联系，明晰算理。）

【教学思考】

（一）沟通联系中体悟转化，明晰算理

依据建构主义学习理论的观点，学生认知结构的重组或扩展是学生主动建构数学知识体系的过程。“沟通联系”可以是认识结构更新的一个策略。本课经历三次沟通：将“借助生活情境解释”与“利用商不变性质解决问题”进行沟通，寻找相同之处，凸显转化思想;结合直观图理解竖式记录每一步的意义，从“数”和“形”两个角度理解被除数和除数同步转化的过程;将横式表征、直观图表征与竖式记录进行沟通并建立联系，理解转化，揭示转化的本质——细化计数单位。在这三次沟通中，建立了“除数是小数的小数除法”与“除数是整数的小数除法”之间的联系，促进了认知的同化和顺应，沟通了小数除法的算理本质，完善了“小数除法”的认知结构。

（二）解释说理中理解意义，发展思维

计算的本质是推理，计算的过程也是逻辑推理的过程。因此，本课的教学，多次通过“你是怎么想的？”“为什么可以这样列？”“理由是什么？”这样的问题引导学生进行解释说理，理解算法的意义所在。这样的过程也让学生经历了逻辑推理的过程，将计算与思考进一步统一，对逐步提高儿童的思维水平应当有所裨益。

参考文献：

[1]石秀荣，贾海林.剩之愈小，割之弥细：小学数学五年级上册《小数除法》单元“深度学习”案例[J].基础教育课程，2017（5）：20-25.

[2]郜舒竹.小学数学这样教[M].上海：华东师范大学出版社，2015：102-105.

[3]张冬梅.主动建构 理法相融 促进生长：以《分数乘整数》教学为例谈计算教学[J].小学教学设计，2021（6）：33-35.

（浙江省杭州市天长小学   310006）