数学规律探究思路的思考

罗嘉裕

2021年的暑假，本人有幸在参与了广州共享课堂越秀小数科教研团队四年级组的研课活动，并执教了四年级上册《积的变化规律》一课。在不断的磨课修改中，我深刻体会到数学规律的学习并不是简单直接灌输的认知过程，只有学生真正通过探究验证获得的规律，才有利于让规律走进学生心里。下面以《积的变化规律》一课为例，浅谈本人对规律探究思路设计的思考。

根据教学目标，《积的变化规律》教学中我们除了要关注知识技能的获得这条明线，同时也要关注隐线——探究规律的能力培养。也就是说除了理解并会运用积的变化规律这个知识点，也要通过探究“积的变化规律”的过程，掌握发现规律的一般方法培养能力。可以说探究过程既帮助学生加深对“积的变化规律”的理解，也锻炼了能力的发展，占有十分重要的位置，也是本课中不可缺席的环节。那么如何设计探究规律的过程发挥教学最大效能呢？

一、显化规律的关键特征

如果没有一定的方向和范围提示，寻找规律将是一件很复杂无头绪的事情。所以从课题入手，显化关键特征，开门见山进行合理联想和分析，就等于抓住规律最突出的特征把复杂问题简单化，以便集中一个方向进行探究。本课题是《积的变化规律》，所以我首先提出一个问题：根据课题你觉得关键词是什么？是“积”和“规律”。“积”说明研究的对象是乘法算式，言外之意就是可以排除加法、减法、除法算式的探究集中火力在乘法算式里。“规律”用于提醒学生回顾以前找规律的经验。暗示学生从观察数与数之间的变化和联系，延展到今天将要学习的从乘法算式里观察因数和积的变化和联系。

二、重演规律的变化过程

因为是探究“积的变化规律”，“变化”说明是动态的。想要充分体现变化的过程就需要从开始到结束演绎出来，而不是出现和呈现结论。例题是出现两组乘法算式然后让学生观察算式，说一说发现了什么（图1）。

结果，学生都把注意力放在数字上，比如：算式中都有“6”“2”“12”等，体现不出“变化”两字。如果在两个算式对应的因数和积之间加入箭头（图2），学生就更容易观察到从上面的数到下面的数有没有变化，进一步再观察它们是如何变化的，然后再对比因数的变化数据和积的变化数据有着怎样的联系和规律。比如图2有三个算式，学生抓不到重点有可能只是横向观察。如果增加了箭頭的提示，学生会从上往下观察算式，第一个因数都是6，因数从2到20变化是乘了10，积从12到120变化也是乘了10，很明显通过把变化用红色字体呈现出来后，对比得出第二个因数和积的变化是一样的。所以动态演绎变化过程可以帮助学生更容易找准规律和理解规律。

三、验证规律的适用范围

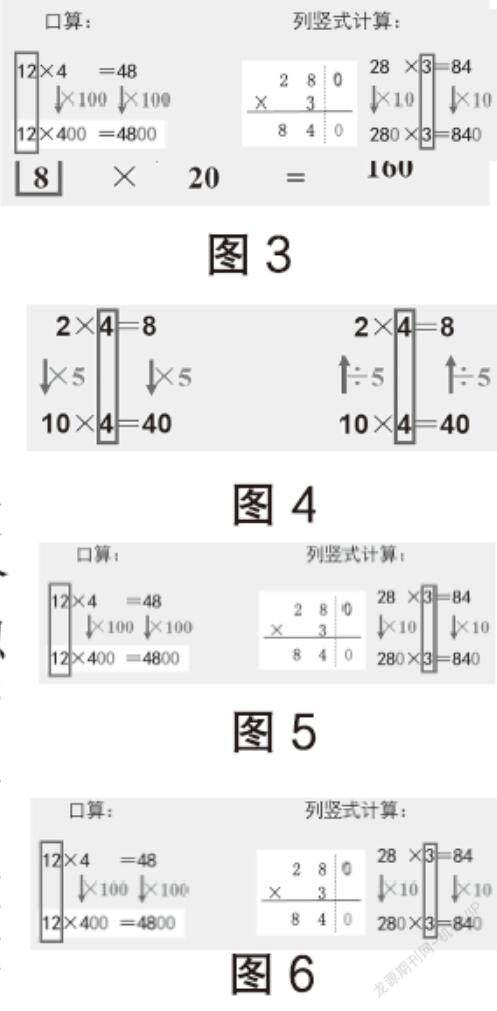
通过重演变化过程发现规律后，由于课本提供的例子毕竟有限，所以我们归纳出来的“规律”确切的说只能算是“猜想”，并没有通过更多更具典型的实例进行验证。那么如何选取例子让规律更具说服力呢？例如为了证明两个因数中有一个因数不变，另一个因数和积变化相同。我们除了书本上出现的“乘10、乘100、除以2、除以4”这些变化的例子，还可以找“乘10、100以外的其它数”或者“除以2、4以外的其它数”等作为例子，进行尝试验证（图3）。或者用同一组算式从不同的角度观察，比如先从上往下观察，再从下往上观察因数与积的变化，看看是否符合规律特点（图4）。也可以用以前学过的旧知识解释新规律，让学生学会举一反三融会贯通（图5）。还可以用逆序思考，假设一个因数不变，积乘几，另一个因数会不会也跟着乘相同的数，来加以验证规律（图6）。只要验证的形式越多学生对规律的理解越深刻。

综上所述，规律的获得其实很需要在探究中明晰其意义，理解其内涵的。但在实际教学中，我们往往会淡化了对规律得出过程的教学探究，重结论、轻过程、重知识、轻方法。把大量的时间放在题海练习上却不肯充分把时间留给学生探索规律的形成过程，本末倒置。我认为，探究规律的教学中可按照：“显化特征——重演过程——验证规律”的思路进行，这种探究路径更有助于学生更深入理解规律的本质，并内化升华。

（责任编辑：张晓东）