咬定“基本思想”?促进数学素养提升

葛敏辉

【摘 要】培养学生的数学思想方法是数学教学的核心使命所在，是一个长期且复杂的过程。因此，教师要善于创设学习情境，把抽象思想、推理思想和模型思想等有机地融合在数学知识之中，让学生在学习实践中受到影响，得到浸染，从而让他们的数学思考更灵动。

【关键词】基本思想 数学教学 数学素养

《义务教育数学课程标准（2011年版）》倡导数学教学要实现由“双基”向“四基”的转变，这是赋予数学教学的新使命，也是更好地满足学生的切实需求和全面发展需要。因此在小学数学教学中，教师应把“数学思想”和“数学活动经验”放到一定的高度上去考虑，努力创设合适的问题情境，引领学生在实践操作、反思学习等活动中，不断积累数学经验，培养基本数学思想，从而让他们的数学素养在学习活动中得到更好发展。

一、渗透抽象思想，让学习思考更灵动

史宁中教授指出，数学的基本思想有三个：抽象、推理、模型，从中可以看出培养和发展学生抽象能力的重要性。抽象思想涉及面极为广泛，包括分类、集合、对应、符号化等数学思想，所以在教学中，教师应审时度势，科学渗透，灵活渗透，让学生在真切的体验感悟中形成最有效的抽象思想，从而更科学地解读数学现象背后的本质，使得概念、法则等的建构有序、科学。

如在“三角形的分类”教学中，为帮助学生更科学地理解三角形按角分类的标准，掌握分类知识，教师可引导学生在分析、比较等学习基础上，逐步抽象出概念，并形成相应的集合。

师：请看屏幕，用自己的方法判断三角形中3个内角分别是什么角？

（学生活动：有的用量角器测量每一个角的度数，有的则用三角板的直角去比对）

生1：我是用量角器测量的，发现1号三角形有3个锐角，2号三角形有1个直角和2个锐角，3号三角形还没有测量出来。

生2：我是用三角板中的直角去比的，发现1号三角形的3个角都是锐角，2号三角形中有1个直角、2个锐角，3号三角形中有1个钝角、2个锐角，4号三角形中有2个锐角、1个直角，5号三角形中有2个锐角、1个钝角，6号三角形中有3个锐角。

师：大家的测量还是挺准确的。想想，根据这些测量情况，如果把這6个三角形分成不同的类别，你认为该如何分？

生1：1号和6号是一类，它们都含有3个锐角。

生2：2号和4号一样，有1个直角、2个锐角。

生3：3号和5号是相同的，有1个钝角、2个锐角。

师：分得很有水平。其实，这样的分法都是按照角的大小来划分的，有自己的名字。谁来给它们命名一下？

生1：全是锐角的1号、6号叫作锐角三角形。

师：你的概括真好！是的，三角形中的3个角都是锐角，它叫作锐角三角形。那其他两类又该怎么起名字呢？

生1：有钝角的，叫作钝锐三角形。

生2：我怎么觉得这个名字这么难听啊！

生3：肯定难听啊，书中没有这样的名字，应该叫作钝角三角形。

师：真棒！预习是好习惯。

生4：那有一个角是直角，就是直角三角形了。

学生的数学学习需要亲身体验的历程，这样他们才有可能在纷繁的数学现象中发现端倪，找到规律，从而实现学习的突破。案例中，教师采取开放式的教学引导学生先观察、判断三角形内角的情况，再尝试分类、学着命名，使得学生学习更加主动。学生在思维碰撞中得出三角形的分类方法，整个学习体验更深刻，学习效果更显著。

二、渗透推理思想，让学习思考更理性

数学学习需要理性的思考，更需要理性的思想作支撑。因此在小学数学教学中，教师应把归纳思想、类比思想、数形结合思想、演绎推理思想等基本数学思想纳入教学中，让学生在知识探究中感悟到数学基本思想，积累相应的数学基本思想，也让基本的数学活动经验等获得发展，从而让学生的数学学习更加理性，数学素养不断丰厚。

如在教学“多边形内角和的推导”时，教师要重视数学思想的渗透，创设必要的活动情境，让学生在具体的活动中学会列举，学会归纳，并在这些活动中类推出多边形的内角和，从而帮助学生建构对应的学习认知。

（出示一组三角形图片，图略）

师：看一看下列图形，从中你想到了什么？

生1：这是三角形，有钝角三角形、锐角三角形和直角三角形。它们都是由三条线段围成的。

生2：它们有三个角，其中至少有2个角是锐角。

生3：三角形的内角和是180度。

师：很好！那老师把两个三角形拼成一个大三角形，那大三角形的内角和是多少度？

生1：360度。

生2：不对！任何三角形的内角和都是180度。

师：真棒！那把一个三角形分成3个小三角形，其中1个小三角形的内角和是多少度呢？

生：180度。

师：不错！看看下面的图形，猜猜它的内角和是多少度？（如图1）

生1：四边形，我猜是360度，因为正方形、长方形也是四边形，它们的内角和都是360度。

生2：我们可以测量，把4个内角相加。

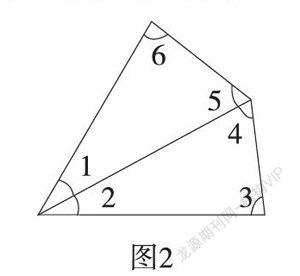
生3：不需要，看，可以把四边形这样分一分，就分成了两个三角形，它们的6个角就是四边形的4个角，所以四边形的内角和是360度。（如图2）

生4：这个办法真好！我们是不是可以用这个方法去思考其他的图形呢？

师：你真爱思考！那就用这种方法去试试五边形看看？

（学生探究五边形的划分，总结对应的方法）

师：那六边形、七边形、八边形呢？

（学生在问题的引领下进行必要的实践探索，在活动中感悟规律，抽象出公式）

生1：四边形分成2个三角形，五边形分成的是3个三角形 ，六边形分成了4个三角形……我发现三角形的个数总比边数少2。

生2：是的！把多边形分成若干个三角形，三角形的个数都比边数少2。

师：光知道这个规律还不够，那多边形的内角和呢？

生：知道多边形能分成几个三角形之后就简单了，用几乘180度就可以了。

师：能不能用一种公式样的方式来表示这个发现呢？

生：边数减2，再乘以180度。

培养学生的数学思想，不是纯粹地传授或灌输就能奏效的，而是要把它们糅合于知识学习之中、问题探究之中。所以在教学中，教师要创设实践探究的氛围，让学生在动手操作中发现规律、提炼规律，最终抽象出概念，从而让数学思维得以有效地渗透。案例中，教师引导学生从四边形、五边形等实践研究中找到规律，并让学生抽象出规律，从而实现列举、类推和抽象思想的不断发展。同时，引导学生活动，说图意、说猜想等，让学生把数量关系与直观的几何图形、位置关系结合起来，使得数形结合思想在学生学习中得到很好的渗透，从而助推有效学习向纵深发展。

三、渗透模型思想，让学习思考更智慧

模型思想是新课标所倡导的十大核心素养之一。它主要包括简化、量化、函数、方程、优化、统计等思想方法。从中不难看出，它是学生研究问题、解决问题的重要素养所在。因此在小学数学教学中，教师应深究教学内容，把握准知识与数学思想之间的联系，科学地将数学思想方法渗透于学生的学习活动之中，让他们的数学思考更理性，数学学习更加务实高效。

如在“9+几”的教学活动中，教师要重视优化思想的渗透，让学生在真切的学习体验中掌握简约学习的策略，使得计算思考更加便捷，充满灵性。

（出示习题：9+5）

师：读一读这个式子，并想一想这道习题该如何思考。

（学生读题目，并在小组中交流自己的想法）

生1：我是数出来的，9后面是10，11，12，13，14，刚好数5次，就是14。

生2：我们学习过9+1=10，于是我把5分成1和4，1和9合成10，10再加4是14。

生3：9+5，我把9分成4和5，5加上5是10，10再加上4就是14了。

生4：9比10少1，10+5=15，再少1，是15-1=14。

学生的数学学习本身就是一个生动活泼、充满理性的过程。案例中，学生的表现可谓是精彩纷呈。有学生把计算思考看成数数来计算，使得计算在数数活动中得以突破。有学生则把前面研究的“10的组成”运用到“9+几”的学习之中，使得“凑十法”的雏形得以呈现，让学生在学习中形成新的思想，建构“凑十法”数学模型，从而使学习更加理性，也富有灵性。而学生的第四种思考则更加理性，他们已经初步掌握了推理策略，使得“9+几”的思考更加缜密。当然，在这个学习过程中，教师要做一个智者，一方面要鼓励学生发散思考、周密思考;另一方面还得重视分析、比较、反思等思維的引导，让学生在比较中深入理解“凑十法” 的便利与灵动，从而诱使学生深入学习“凑十法”，理解“凑十法”，进而帮助学生建构对应的数学模型，为他们深入学习加法提供经验支持和思想支持。

总之，在小学数学教学中，教师应学会抓住契机，在学生的知识学习活动中有机渗透相应的数学思想，以促进学生的数学素养不断发展。当然，我们还应认识到，学生的数学思想形成与发展是远远不能等同于数学知识的学习与技能的形成的，不是靠一定量和有难度的训练就能速成的，而是需要一个不断历炼的历程。这是一个润物无声的过程，只有在教师潜移默化的影响下数学思想才会在学生的数学学习中不断生成，持续生长。因此，教师要做一个有心人，在平时的教学中重视数学思想的挖掘、归纳与提炼，并持之以恒地渗透于数学教学之中。

【参考文献】

[1]褚小芹.积累数学活动经验 促进数学素养提升[J].小学教学参考， 2013（14）.

[2]张久权.落实课程标准，帮助学生积累基本思想[J].数学学习与研究， 2013（16）.

[3]孙传松.对中学数学核心素养的几点认识[J].西藏教育， 2017（4）.