图强化典型相关分析及在图像识别中的应用

苏树智 谢 军 平昕瑞 高鹏连

①(安徽理工大学计算机科学与工程学院 淮南 232001)

②(合肥综合性国家科学中心能源研究院(安徽省能源实验室) 合肥 230031)

③(安徽理工大学数学与大数据学院 淮南 232001)

1 引言

特征提取[1,2]是解决分类和识别任务的一类主流方法，从模态数据种类角度划分，可分为单模态方法和多模态方法。在单模态方法中主成分分析(Principal Component Analysis, PCA)[3,4]使用最为广泛，其通过正交变换从原始单模态数据[5,6]的高维空间中抽取数据的低维表示形式，同时最大化低维数据的差异。但是PCA是一种线性特征提取方法，没有考虑数据的内在结构信息，因此在很多实际应用中难以抽取强鉴别力的低维特征。而多模态方法则是处理两种或两种以上模态数据的方法，典型相关分析(Canonical Correlation Analysis,CCA)[7]是多模态特征提取方法中的代表算法，能够实现高维多模态数据的特征提取和融合。

CCA旨在学习两组模态数据的相关投影方向，使投影后的两组模态间相关性最大，目前已应用于图像处理[8]、特征融合[9]等领域。但CCA本身和PCA均为线性方法，针对其难以提取高维非线性数据有效特征的问题，文献[10,11]中提出局部保持CCA(Locality Preserving Canonical Correlation Analysis, LPCCA)，该方法考虑局部邻域间的关系，利用局部的几何结构解决一些非线性问题。虽然LPCCA比CCA更好地揭示了内在数据结构，但是保留的局部信息多包含噪声，揭示的近邻结构存在失真现象，因此仅在姿态估计任务中获得了良好的实验结果，而分类能力较差。为了解决LPCCA的弱分类性能问题，文献[12]提出一种新的可替代局部保持CCA(Alternative Locality-Preserving Canonical Correlation Analysis, ALPCCA)，该算法对LPCCA整体近邻几何结构的嵌入方式加以改进，进而提升了识别性能。

此外使用核的思想也可以解决非线性问题，文献[13,14]提出的核CCA(Kernel Canonical Correlation Analysis, KCCA)利用核函数在更高维空间中表示原高维数据，令原高维数据在更高维空间中线性可分，尽管KCCA在分类性能上有所提升，但将高维数据映射到更高维大大增加了运算过程的计算量。

除了考虑数据结构信息外还可以利用标签信息和图的思想提升算法的性能。标签信息即一种有效的监督信息，鉴别CCA(Discriminative Canonical Correlation Analysis, DCCA)在文献[15,16]被中提出，将监督信息融合到特征提取的框架中，在子空间中类内样本分布更加紧密，类间样本离散程度更大，从而使其在分类任务中拥有较好的类分离性。而图多视角CCA(Graph Multiview Canonical Correlation Analysis, GMCCA)[17,18]则通过使用图诱导的方式直接分析数据间的内在关系，减少规范变量与常见的低维表示形式之间的距离。

上述方法是基于原始高维数据确定近邻关系或构建图，但因噪声和冗余信息，这种近邻关系或图揭示的几何结构会存在失真现象，降低特征的鉴别性。本文提出一种新的图强化典型相关分析(Graph Enhanced Canonical Correlation Analysis, GECCA)算法。该算法使用谱聚类方法对原始高维数据进行分割，获取多种数据成分，并针对每种数据成分构建对应成分图，可从不同成分的角度出发更好地揭示高维数据间复杂几何流形；为了获得益于分类和识别任务的信息，采用相似准则构建成分图的权重矩阵，借助概率评估方法保留成分图对应的类监督信息，以此构建成分图的类系数矩阵；通过图强化方式将成分图的权重矩阵和类系数矩阵进行融合得到强化矩阵，并将其嵌入到典型相关分析的框架中。GECCA更好地揭示和保留了隐藏在原始高维数据中的几何流形和鉴别信息，从而能够更好地指导和辅助特征的提取。GECCA有以下特点：(1)能更好地揭示数据的本质几何流形，解决非线性特征提取问题；(2)有效地利用了监督信息，使其在图像识别任务中拥有良好的类分离性。

2 算法回顾

本节将简要回顾CCA算法的主要内容。CCA为两种模态数据学习一个相关子空间，使得在子空间中两种模态数据的相关性最大。两种模态数据集可分别用X和Y表示，且所有样本均一一对应，其中X=[x1,x2,...,xn]∈Rp×n,Y=[y1,y2,...,yn]∈Rq×n。每种模态数据集都有n个样本，xi,yi(i=1,2,...,n) 表示数据集X,Y中第i个样本，且样本均为均值化后的样本数据，X数据集中数据维度是p，Y数据集中数据维度是q。CCA可简化为使模态间相关性最大的投影方向(α,β)学习问题

由于投影方向的尺度不变性，上述投影方向的学习问题能够进一步简化如式(2)的优化模型

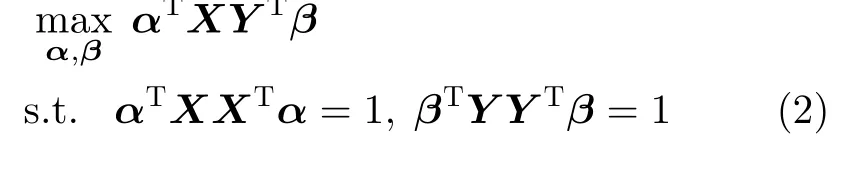
3 图强化典型相关分析(GECCA)

3.1 CCA的等价描述

CCA的优化函数可等价于两模态间样本距离最小，因此可将其等价描述为

3.2 成分图权重矩阵的构建

对于给定两组对应模态数据集X和Y，数据样本间通常包含不同的几何结构信息，为了有效利用这些信息本文提出图强化的方法。

每个模态数据集在原始高维数据中通常包含多种独立数据成分，例如一张照片中人物和背景即为两种不同数据成分，利用原始数据直接构图的方法无法反映不同数据成分间的关系。GECCA先将上述数据集X和Y采用谱聚类方法进行分割，将不同数据中同一成分的数据分割在一块，分割后得到原始高维数据的多重数据成分集，并为每种数据成分构建对应成分图，以此保留数据间的内在联系，使用相似准则构建成分图权重矩阵，揭示原始数据中的复杂内在流形结构，流程如图1所示。从优化角度来看没有区分各成分的重要性，所以本文采用线性融合策略进行图强化，根据标签信息获取类系数矩阵以此作为图强化的优化系数。

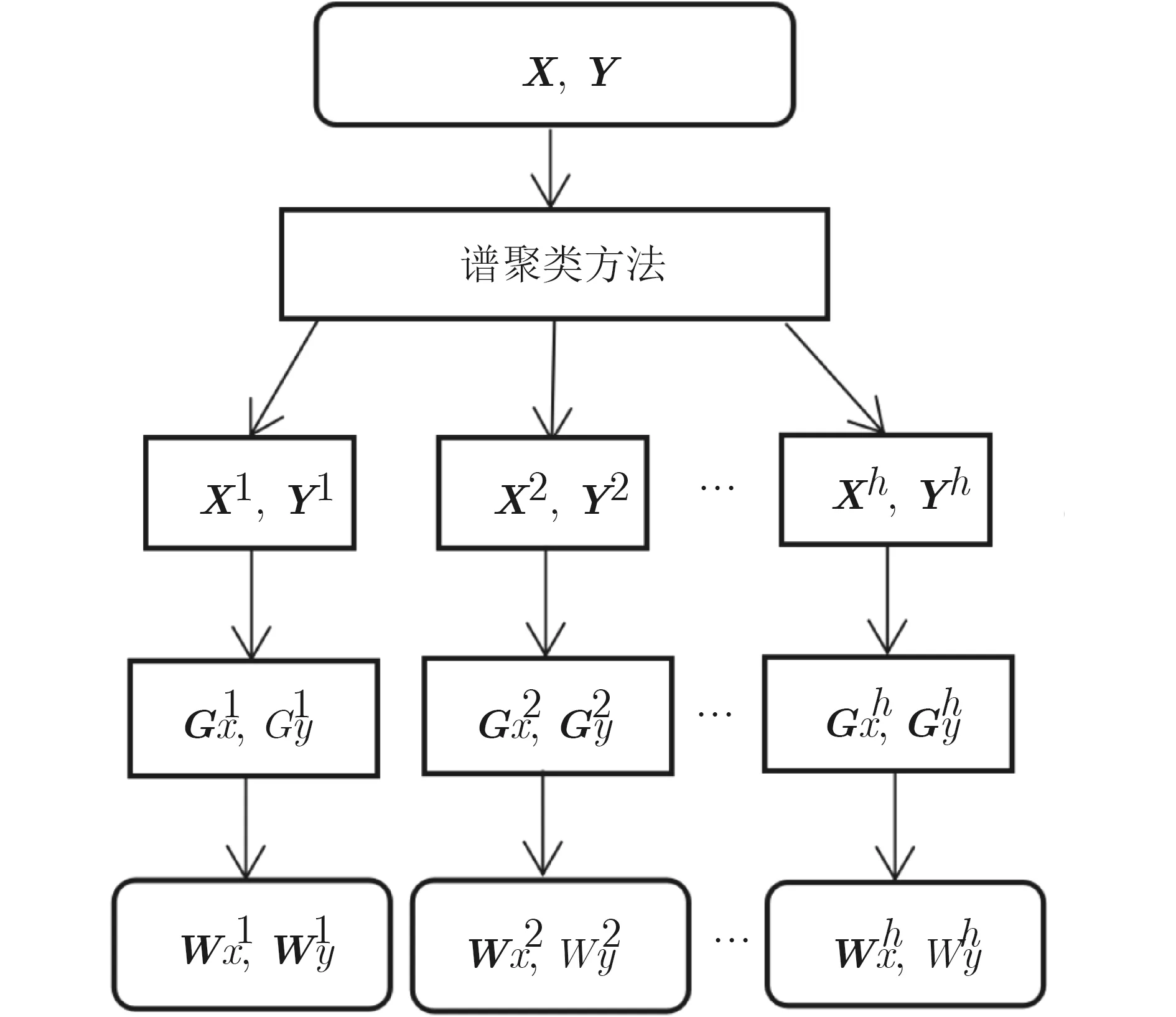
图1 成分图权重矩阵流程图

3.3 类系数矩阵的构建

3.4 GECCA的优化模型

为优化模型，可将式(14)在代数运算后重写为(忽略一般性常数)

3.5 GECCA的求解

对式(15)中模型进行求解，首先为该模型构建拉格朗日乘子函数

3.6 特征融合方法

利用求得的相关投影矩阵A和B可得到数据集X和Y对应的低维相关特征训练集ATX ∈Rd×n和BTY ∈Rd×n。本文采用并行特征融合策略完成特征融合

融合后获得的训练集在子空间低维融合特征集可记作Z={Z1,Z2,...,Zn}∈Rd×n。采用同样方法可得到测试集低维融合特征集。

4 实验部分

为评估GECCA的图像识别性能，分别在人脸数据集XM2VTS和手写体数字数据集Semeion上设计了针对性实验。利用模态策略[19]获得上述数据集的模态数据，具体为采用Coiflets和Daubechies两种小波变换得到每个图像的低频子图，为了弱化小样本问题，可用PCA将低频子图约简到100维，以此作为每幅图形的两种模态数据。在实验中将GECCA算法与DCCA[16], CCA[7], LPCCA[10], ALPCCA[12]算法作对比分析，并且所有算法的最终识别率均利用基于欧氏距离的最近邻分类器来获得。

4.1 XM2VTS人脸图像数据集上的实验

XM2VTS人脸数据集包含来自295名志愿者每人4个会话中的8幅图像，图2为XM2VTS数据集中部分人脸图片。本实验从每类样本中进行10次随机抽取，每次抽取t(t=3,4,5,6)个样本作为训练样本，其余样本作为本次实验的测试样本。图3展示了在人脸数据集上识别率随维度变化情况。

图2 XM2VTS部分人脸图像

CCA没有考虑数据间内在几何关系和类标签信息，只是将投影后两模态间的相关性最大化，无法掌握数据中非线性几何结构，学习的低维特征在图像识别中鉴别力不足。LPCCA和ALPCCA都在一定程度上考虑了高维数据中的内在联系，在相关子空间中尽可能保留数据的几何结构；但LPCCA直接利用原始的高维数据揭示的局部近邻结构，会受到高维数据中包含的噪声和冗余信息的影响，保留的局部近邻结构容易失真，所以识别效果较差；ALPCCA也使用原始高维数据，与LPCCA不同，采用的是两模态整体近邻结构的等权线性表示，因此识别率要高于LPCCA。DCCA在相关系分析框架中加入了监督信息，对高维数据进行约束，具有较高识别率。

表1 GECCA的算法步骤

GECCA利用成分图的方式揭示数据中各成分之间的联系，用成分图权重矩阵保留数据的几何流形，并借助类系数矩阵优化成分图权重矩阵，使得低维相关特征更具鉴别力。从图3中不难看出，在不同个数训练样本下GECCA均展示出最佳识别率，且识别率在较低维度时增幅最快说明GECCA提取的特征鉴别能力更强。

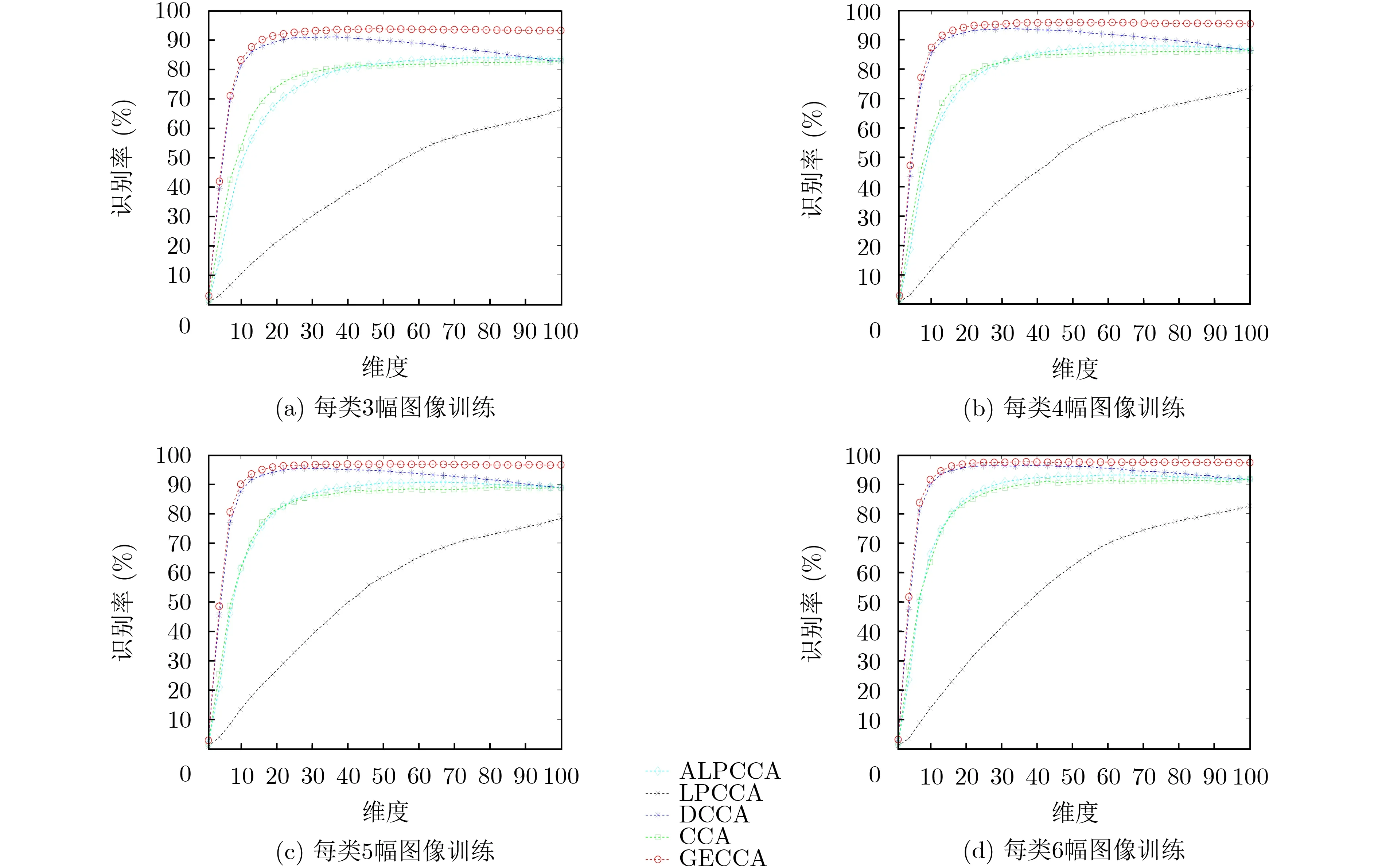
图3 在XM2VTS人脸数据集上识别率随维度变化情况

4.2 在Semeion手写体数字数据集上的实验

Semeion手写体数字数据集包含大约80个人的1593个手写体数字，每人写出由0到9的所有数字。该数据集中每类有大量数据样本，因此本实验从每类中选择t(t=40, 60, 80, 100)个样本用于训练，剩余样本用作实验测试，并进行10次随机性测试。图4为每次随机实验各算法的最佳识别率立体图，表2记录各算法平均最佳识别率及标准差。

CCA是一种线性方法，无法发现隐藏在高维数据中的非线性几何结构，因此会影响识别性能。LPCCA是将全局非线性转化为局部线性，解决姿态估计中的非线性问题，但鉴别能力受原始高维数据中的噪声和冗余信息的影响，表现出了较差的识别性能。ALPCCA对LPCCA邻域信息的利用加以改进，使之鉴别能力得以提升。类标签作为一种重要的监督信息，可提升算法的识别和分类性能，但CCA, LPCCA和ALPCCA均未用到标签信息，因此识别率均低于包含类标签约束的DCCA。

GECCA通过图强化方法将成分图权重矩阵和类系数矩阵线性融合，并将其嵌入到相关特征学习的理论框架中，使其在保留成分数据间关系的同时具有鉴别效果；此外，GECCA对模态内样本的散布进行约束，使得同类样本间的距离更近，分类性更强。如图4所示，不难发现在训练样本情况不同时，10次随机实验中GECCA均表现出最佳鉴别能力，这表明GECCA的识别效果优于其他算法。在表2中，GECCA具有最高的平均识别率和更小的标准差，说明GECCA在相同训练样本下更加稳定，有更小的误差，实验对随机样本有更好的鲁棒性。

表2 在Semeion手写体数字数据集上的识别率及标准差

图4 在Semeion数据集中每次随机实验的最佳识别率

5 结束语

CCA作为一种线性多模态特征学习方法，无法解决高维数据的非线性问题。而基于局部领域的特征提取方法的几何结构往往会因噪声和冗余信息存在失真现象，从而影响低维特征的类分离性。在原始高维数据中通常包含多种独立的数据成分，仅使用一个图难以反映不同数据成分之间的差异。为此，本文提出了一种新的GECCA算法，该方法考虑了原始数据中的几何信息和监督信息。采用成分图权重矩阵揭示数据内在本质几何流形；以类系数矩阵方式增加数据的可分类性；以此为基础，通过图强化将成分图权重矩阵和类系数矩阵进行融合，并嵌入到相关特征提取框架中，减小直接使用原始数据而保留噪声的影响，同时增强算法的识别和分类性能。在XM2VTS人脸数据集和Semeion手写体数字数据集上进行实验，良好的实验结果显示GECCA是一种有效的图像识别算法。

本文为未来的研究开辟了几个有趣的方向。将两模态数据融合扩展至3个或3个以上模态值得进一步探究。将全监督改为半监督也具有十分重要的现实意义。