SIMON类非线性函数的线性性质研究
关 杰 卢健伟
(战略支援部队信息工程大学 郑州 450001)
1 引言
随着技术的快速发展,信息处理功能已经可以在越来越小的嵌入式设备中实现。这类微型嵌入式设备的计算与存储能力十分有限,因此称为资源受限设备。传统密码在设计上主要考虑提高算法的安全性,没有考虑将算法应用于受限设备的情况。轻量级密码(LightWeight Cryptography, LWC)的诞生给这类设备所处理的信息提供了相应的保护,成为密码学研究的热点之一。
SIMON算法[1]是美国国家安全局(the National Security Agency, NSA)在2013年设计的一类基于Feistel结构的轻量级分组密码算法,该算法的轮函数为F182(x)=(x<<<1)&(x<<<8)⊕(x<<<2),只包含循环移位、按位与和异或这3类基本运算,因此软件与硬件的实现效果较好。自从SIMON算法提出以来,密码学者对其进行了大量分析。目前针对该算法的安全性分析主要包括差分分析[2-4]、线性分析[5-9]、不可能差分分析[10-12]、零相关分析[13-15]和积分分析[16,17]等。
SIMECK算法[18]是于2015年设计的一类轻量级分组密码算法,其结合了SIMON算法和 SPECK算法的优点,具有高效且低成本硬件实现的特点。该算 法 的 轮 函 数 为F051(x)=x&(x<<<5)⊕(x<<<1),同样沿用了SIMON算法轮函数的结构,将循环移位参数由(1,8,2)修改为(0,5,1)。
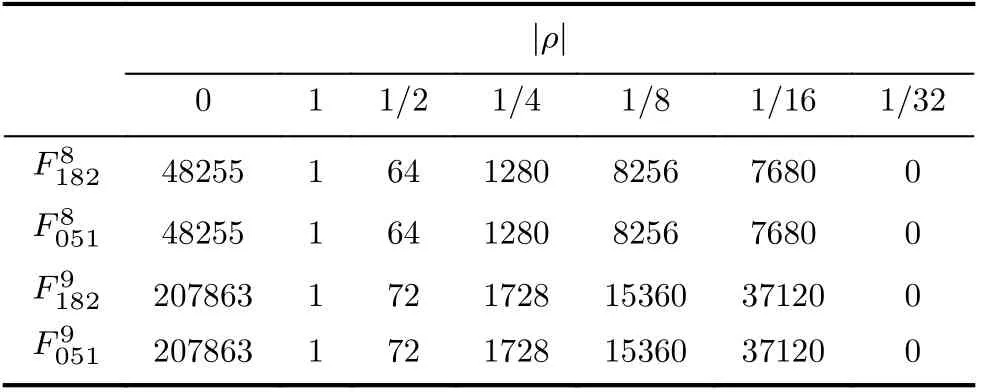
这些算法的轮函数均采用了如下形式的非线性函数Fabc(x)=(x<< 本文主要研究了移位参数一般化的SIMON类算法轮函数Fabc(x)的线性性质,给出了相关优势的取值范围,并且证明了对于该范围内的每一个相关优势,都可以找到对应的掩码对,解决了这类轮函数的Walsh谱分布规律问题,同时给出了非平凡相关优势取到 2−1与最小值的充分必要条件与计数情况,为SIMON系列算法与SIMECK算法等的线性安全性分析提供了理论基础。 本文组织架构如下:第2节介绍SIMON类算法轮函数、不相交2次型以及线性相关优势等基本概念,第3节给出SIMON类非线性函数的线性性质,第4节进行全文总结。 录),可以有效地将任意给定的2次布尔函数转换为不相交2次型。 下面考虑掩码对计数问题,由上述证明过程可知,一个输出掩码µ对应4个输入掩码η,故当w(µ)=1 时掩码对数为4n,当w(µ)=2时,取遍i0后,µi0=µi0+t=1与µi0=µi0+n−t=1包 含 的µ的集合相同,故此时掩码对数为4n,总计8n。证毕 定理4研究了最大非平凡相关优势点的结构和计数,但是最小非平凡相关优势点的结构和计数也是需要重点考虑的问题。下面给出特定条件下非平凡相关优势取到最小值的充分必要条件。 结合定理5,给出非平凡相关优势取到最小值1/2n/2时的一个充分条件。 表1 F abc(x)相关优势计数表 文献[5]仅给出了SIMON类轮函数的线性逼近式的2次项相互独立时的线性性质,然而2次项相关时的线性性质还未彻底解决。本文进一步研究了移位参数一般化下SIMON类算法轮函数的线性性质,利用算法1将相关优势取值问题转化为不相交2次型中2次项的个数问题,界定了相关优势的取值范围,证明了在特定条件下对于该范围内的每一个相关优势点均可找到对应的掩码对,证明了此类函数是多输出部分bent函数,给出了非平凡相关优势取到最大值1/2时掩码对的充要条件及计数,给出了特定条件下非平凡相关优势取到最小值的充分条件与掩码对的计数。研究表明,当n为 偶数且t为奇数时,可以取到最小非平凡相关优势点。该研究成果为SIMON与SIMECK等算法的线性分析提供了理论基础。接下来需要做的工作是给出此类函数移位参数抵抗各类密码分析方法的选取准则,并应用于SIMON与SIMECK等算法的线性安全性分析。 表2 转变成不相交2次型算法(算法1) 续表22 基本概念




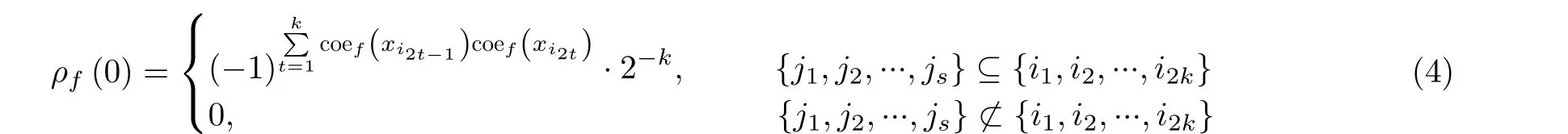


3.1 F 谱值的取值范围















4 结束语
5 附录