基于二阶对抗样本的对抗训练防御

钱亚冠 张锡敏 王 滨 顾钊铨 李 蔚 云本胜

①(浙江科技学院理学院/大数据学院 杭州 310023)

②(杭州海康威视网络与信息安全实验室 杭州 310052)

③(广州大学网络空间先进技术研究院 广州 510006)

1 引言

深度神经网络(DNN)在生物信息学[1,2]、语音识别[3,4]和计算机视觉[5,6]等领域获得成功应用的同时，研究者们发现DNN容易受到对抗样本的攻击[7]，即在自然图像中添加微小的扰动，可以欺骗DNN做出错误预测。由于对抗样本具有较好的隐蔽性，不易被人眼发现，给安全敏感的应用带来很大的破坏性。例如，在自动驾驶领域，研究者们通过在道路交通标志图片上添加微小扰动得到对抗样本，导致采用DNN进行道路交通标志识别的自动驾驶汽车做出错误判断，引起交通事故的发生[8]。自动驾驶系统可能会遇到的道路交通标志图片及其对应的对抗样本，对于人眼来说，两张图片是相同的，同为注意危险标志。而自动驾驶系统中的DNN则把对抗样本判断为让行标志。这意味着难以察觉的扰动有可能使一辆毫无故障的自动驾驶汽车做出危险的行为。因此，对于对抗样本的防御研究具有现实意义。

自Szegedy等人[7]发现DNN中存在对抗样本以来，研究者们提出了一系列对抗样本的生成与防御方法。生成对抗样本的过程通常被建模为一个有约束优化的问题，其目标是在约束条件下最大化损失函数。现有的典型对抗样本包括C&W[9], Deepfool[10],FGSM[11], PGD[12], M-DI2-FGSM[13]等。同时，研究者们提出了多种防御对抗样本的方法，如防御蒸馏[14]、对抗训练[15]、强化网络[16]及对抗样本检测[17]等。

在大部分防御方法被文献[18]证实防御效果有限的情况下，对抗训练是少数被经验证明为目前最为有效的防御方法。对抗训练最早由Szegedy等人[7]提出，通过将对抗样本注入训练过程，以增强DNN的鲁棒性。随着研究的深入，Madry等人[13]将对抗训练形式化为由内部最大化问题和外部最小化问题组成的鞍点问题，即存在对抗样本最大化损失函数的情况下，优化模型参数实现损失函数最小化。按照Madry等人的鞍点理论，解决内部最大化问题需要更强的对抗样本，他们提出了基于PGD(1阶梯度投影)的对抗训练方法，实验证明能够防御大部分1阶梯度攻击。但是1阶梯度对于DNN的逼近能力有限，无法进一步找到更强大的对抗样本，因而也无法训练出更鲁棒的DNN。基于这个思路，本文提出于基于2阶梯度的对抗样本生成方法。与以往线性逼近方法不同，在输入样本的微小邻域内，对DNN损失函数进行2阶多项式逼近。本文提出的方法优点是，利用Hesse矩阵可提取到损失函数在输入邻域内的更多信息，从而更好地解决内部最大化问题。

本文分别从理论和实验角度证明了2阶对抗样本强于PGD对抗样本。本文提出将对抗样本的扰动下界，即攻击成功所需的最少扰动，用于衡量不同对抗样本的强度。计算结果显示，2阶对抗样本的扰动下界低于PGD，即2阶对抗样本攻击成功所需的最少扰动少于PGD，这意味着2阶对抗样本强于PGD。在MNIST和CIFAR10上的实验结果验证了本文的理论分析：(1) 相较于包括PGD在内的现有典型对抗样本，2阶对抗样本能够在添加更少扰动同时，达到更高的攻击成功率；(2) 基于2阶对抗样本的对抗训练能够防御现有的典型1阶对抗攻击。

2 预备知识

2.1 深度神经网络

2.2 对抗样本

2.3 威胁模型

目前有很多对抗样本的生成方法，但这些方法都是在一定的假设限制下进行的[9]。由于对手的攻击行为很大程度上决定了对抗样本的强度。如果攻击行为不被限制，对手甚至可以使用任意图像替换给定的图像，这就违背了对抗样本的定义。为此，我们把这些攻击行为定义为威胁模型，通常包含攻击目标和攻击能力。

(1) 攻击目标

威胁模型中的攻击目标可以被定义为一个需要被检测和防御的具体式子。在DNN中，对于攻击目标的划分有利于我们明确这个具体式子。因此，威胁模型中，对于攻击目标的划分至关重要。可以将攻击目标具体划分为2类，包括无目标攻击和有目标攻击。无目标攻击是指改变对抗样本的类别至任意一个非正确类。有目标攻击是指改变对抗样本的类别至指定的一个非正确类。正式地说，有目标攻击是无目标攻击的一个子集，而对于对抗样本的防御方法来说，防御两者的难易程度并不会有所区别。因此，本文提出的2阶对抗样本属于目前更为主流的无目标攻击。

(2) 攻击能力

对抗样本还可以根据对手掌握目标分类器信息的多少来定义攻击能力，分为白箱攻击和黑箱攻击。白箱攻击是指攻击者几乎知道关于DNN的所有信息，包括训练数据、激活函数、拓扑结构、权重系数等。黑箱攻击则假设攻击者无法获得已训练的DNN内部信息，仅能获得模型的输出，包含标签和置信度。因为需要掌握目标DNN的梯度信息，2阶对抗样本属于白箱攻击。

3 对抗训练防御方法

3.1 问题的提出

目前最有效的对抗训练方法是由Madry等人[13]提出的PGD对抗训练。从优化的观点出发，对抗训练被定义为关于鞍点的优化问题：

可以发现式(3)是一个内部最大化问题和一个外部最小化问题的组合。内部最大化问题是找到令DNN产生最大损失的对抗样本。外部最小化问题是在某种对抗攻击下，寻找使对抗损失最小的模型参数。由此可见，对抗训练是模型精度和鲁棒性之间的一种最佳平衡。Madry等人[13]认为存在更强大的对抗样本可以更好地解决内部最大化问题，从而训练出更加鲁棒的DNN，但基于一阶对抗样本不能很好地解决这个问题。为此，本文提出2阶对抗样本解决式(3)中的内部最大化问题。

3.2 2阶对抗样本

本节给出了一种对抗样本的2阶生成方法。我们将生成对抗样本的过程定义为一个箱约束的优化问题：

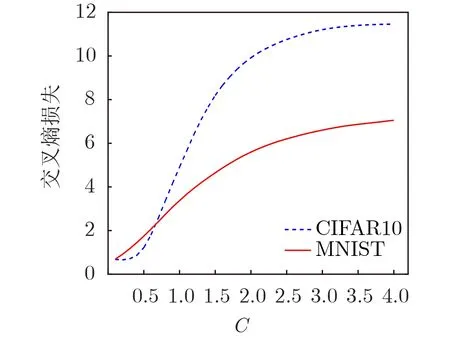
图1 C与优化过程中交叉熵损失函数的关系

表1 基于2阶对抗样本的对抗训练算法

4 理论分析

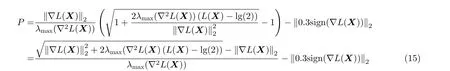
5 实验

通过实验进行验证：(1)相比于以C&W, Deepfool, FGSM, PGD以及M-DI2-FGSM为例的典型对抗样本，2阶对抗样本在具有更高隐蔽性的同时具有更高攻击成功率；(2)相比于PGD对抗训练，基于2阶对抗训练抗御对当前典型对抗样本都具有鲁棒性且具有更高的分类准确率。

5.1 实验设置

本文实验的数据集为MNIST和CIFAR10。MNIST是一个包含从数字0到9的10个类的手写体数据集，共包含70000张手写体数字图像，每个图像的大小为 2 8×28像素。实验选取60000张图像作为训练数据，10000张图像作为测试数据。CIFAR-10数据集由60000个 32×32彩色图像组成，包含10个类。实验选取50000个图像作为训练数据和10000图像作为测试数据。训练集分为5个训练批次，每个批次有10000个图像。对于MNIST我们使用精度为98.79%的标准LeNet网络。对于CIFAR10我们使用精度为76.97%的标准AlexNet网络。

5.2 评估指标

实验使用4个评估指标，包括ℓ2，ℓ∞，PSNR以及ASR。现有的研究普遍用ℓ2的值来衡量全局添加的扰动量，ℓ∞来衡量局部(单个像素)添加的扰动量。峰值信噪比(PSNR)作为最广泛使用的评价图片质量的客观度量，可以对对抗样本的隐蔽性进行有效评估。ASR称为对抗样本的攻击成功率，目前被大多数文献用于衡量攻击能力。若生成对抗样本的成功率不是100%，那么这些数据仅取了成功的那部分作为基数。

5.3 评估2阶对抗样本

本文采用机器学习模型攻防库Cleverhans[19]中的C&W，Deepfool，FGSM，以及由原作者给出代码的PGD和M-DI2-FGSM作比较实验。为保证评估的严谨性，实验采用相同模型架构和测试数据集。其中，C&W的扰动上限δ=0.3 ，ε=0.3，学习率为0.1；Deepfool的参数设置与C&W相同；而FGSM作为单步迭代法，ε=0.3；PGD作为FGSM的衍生方法，迭代扰动固定为ε=0.3；M-DI2-FGSM中，ε=0.3。

实验中，从MNIST与CIFAR中随机取出500张可以被DNN正确判断的图片进行测试，实验结果如表2所示。实验证明，在不同数据集中，相比于现有的典型攻击方法，2阶对抗样本不但攻击成功率更高，而且添加的扰动更少。

表2 不同的对抗样本在MNIST和CIFAR10的对比

5.4 对抗训练2阶对抗样本

本文分别采用自然样例、2阶对抗样本，C&W,Deepfool, M-DI2-FGSM, FGSM以及PGD进行攻击和对抗训练，用于对比攻击效果与防御效果。从MNIST与CIFAR10中随机取出200张可以被初始模型正确判断的图片进行测试。图2是实验结果的热力图表示，横轴表示各种方法产生的对抗样本，纵轴表示用不同对抗样本进行对抗训练得到的对抗训练模型，图中每一个数字代表某一个对抗训练模型对于某一类对抗样本的分类准确率。图2的结果表明：(1)对抗训练产生的对抗训练模型对于特定攻击具有鲁棒性；(2)相比于PGD对抗训练，基于2阶对抗样本的对抗训练防御能够防御现存典型1阶对抗样本，且具有更高的分类准确率。

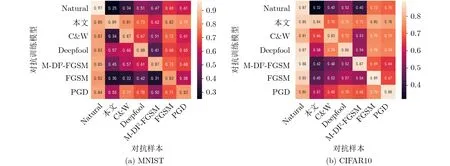
图2 对抗训练DNN对于对抗样本的分类准确率

6 结束语

通过理论分析可知，2阶对抗样本的扰动下界低于1阶最强对抗样本PGD，表明2阶对抗样本强于PGD，能够更好地解决对抗训练的内部最大化问题。在MNIST和CIFAR10数据集上的实验表明，相较于现有的典型1阶对抗样本，2阶对抗样本拥有更高的攻击成功率和更高的隐蔽性。相比于PGD对抗训练，基于2阶对抗样本的对抗训练防御能够防御现存典型1阶对抗样本，且具有更高的分类准确率。2阶对抗样本中参数经验值的选取是通过大量实验得到的，将来对参数的选取机制有待进一步研究。目前还未有研究者对对抗样本的在线攻击与线下攻击进行分析，在未来的工作中，我们将进一步研究2阶对抗样本与其他对抗样本在线攻击与线下攻击的不同特征。