基于FPGA技术的双磁控忆阻Shinriki振荡器对称行为分析

闵富红 郑宏亮 芮 智 曹 弋

(南京师范大学电气与自动化工程学院 南京 210046)

1 引言

基于电路的完备性和基本变量的对称性，1971年文献[1]首次从理论上提出忆阻器的概念。作为一类具有记忆性的非线性二端口元件，忆阻器的伏安特性曲线常表现为斜“8”字型的过零点紧磁滞回线特征[2]。因此，将其与非线性混沌电路结合极易产生丰富的动力学现象。大量研究表明，忆阻混沌电路在神经网络[3]、人工智能[4]、保密通信[5]、信号处理[6]等方面具有广阔的应用前景。因此，多种忆阻电路[7]被相继提出和分析，其中有忆阻超混沌Jerk系统[8]、非自治忆阻FitzHugh-Nagumo电路[9]、忆阻文氏桥振荡器[10]和Sallen-Key低通滤波忆阻振荡器[11]等。

不同于普通非线性电路，忆阻电路往往拥有更为复杂的动力学特性，比如，对称分岔行为、多稳态特性、反单调性和不完全对称行为等。对称性[12]在关于初值对称的忆阻系统中普遍存在，从系统方程中即可看出。而文献[13]在改进型忆阻蔡氏电路中，首次发现了特定参数下系统的对称分岔行为，并通过共存分岔图和李雅普诺夫指数进行揭示。多稳态现象[14]主要表现为依赖于系统初始条件的多种吸引子共存现象。文献[15]构造了基于最简忆阻器的准哈密顿系统，系统无平衡点，但存在无穷多隐藏吸引子，在多稳态现象下揭示系统通过间歇和瞬态混沌走向混沌的途径。反单调现象[16]是当某些特定参数或初值变化时，在参数域或初值域成对产生正向和反向倍周期分岔级联的现象。文献[17]讨论了基于RLCM四元件的混沌电路中，随参数变化出现的正负初值互补共存的周期-混沌气泡。拥有不同拓扑结构吸引子的不完全对称行为[18]通常存在于低维系统中，文献[19]在3阶忆阻HR神经元模型中运用相位图、分岔图和动力学地图等分析方法，揭示了系统存在的不对称共存吸引子的隐藏动力学行为。但是，关于特定参数的对称动力学行为在高维系统中的研究较少。

基于此，本文通过在经典Shinriki振荡器[20]中引入无源和有源磁控忆阻，并在电感支路串联电阻，搭建出一个新型的5维忆阻振荡系统。通过动力学行为分析发现该系统特有的在特定参数下的对称共存分岔现象，并通过Lyapunov指数谱对比验证。同时将这一现象延伸至双参数平面以及参数-初值平面内分析，观察到在对称吸引域内多种运动状态吸引子的共存行为。对系统在对称域内伴随出现的反单调现象、不完全对称行为等进行了重点分析。最后，在FPGA数字平台，对双磁控忆阻Shinriki振荡器开展电路实验，通过仿真波形验证数值分析的正确性以及对称动力学行为的真实存在性。

2 双磁控忆阻Shinriki振荡器模型

图1给出了双磁控忆阻Shinriki振荡器模型，电路结构主要由3个部分构成：负阻抗转换器、非线性正电阻区域以及RLC谐振回路。原电路[20]中负阻抗转换器由两个等值电阻R1和R2、 运算放大器U以及接地电阻R3组成，该部分对外电路表现为−R3，且作为电源向电路其他部分供能。非线性正电阻区域利用一个3次无源磁控忆阻器W1替换原来的二极管串并联支路。负阻抗转换器与非线性正电阻区域间通过R4和电容C0的并联连接在一起。RLC谐振回路的存在，对电路能随机产生振荡波形和周期性波形起到了关键作用，本文中，在电感L支路串联电阻R5，同时将电阻支路用一个3次有源忆阻器W2替代，提高电路的复杂度，便于产生更丰富的非线性动力学现象。新构建的双磁控忆阻Shinriki振荡器包含5个动态元件，分别是电容C0,C，电感L，两个磁控忆阻器W1和W2，对应的状态变量如图1所示为VC0,VC,iL,φ1和φ2。

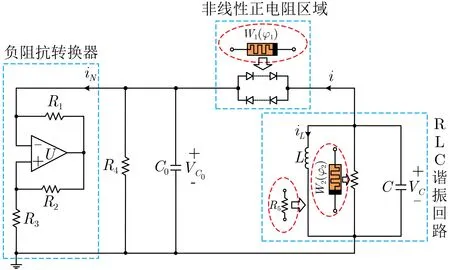
图1 双忆阻Shinriki振荡器模型

3 动力学行为分析

3.1 对称共存分岔行为

为了研究振荡器式(2)在不同单参数变化时产生的分岔行为，给出系统随参数c,d变化的共存分岔图和Lyapunov指数谱如图3所示。其中，参数c表示的是系统中电感L值的倒数，负电阻R3的倒数和正电阻R4倒 数的差值为参数d。 初值设置为(±10−6,±10−6,±10−6,0,0)，固定其它参数如表1所示，在达到起振条件下弱化初值对系统的影响。

表1 系统参数设置值

在图3(a)中，参数c的变化区间为( 14.6,23.8)，可以观察到随着参数c取值的增加，系统先后遍历了混沌态、周期窗、多周期，然后通过反倍周期分岔进入周期一，最后达到稳定不动点状态，其中，周期窗和多周期状态衍生穿插在混沌态之间。当参数c<14.484时，系统处于大周期状态，对应状态变量xmax跃变为极大的值，且最小Lyapunov指数L5骤降为极小的值，考虑到分岔图和Lyapunov指数谱的协调性和可观察性，该部分区间未在图3(a)和图3(b)中给出，后续的分析中会加以说明。在c ∈(14.484,16.31)∪(16.684,18.928)时，系统产生混沌吸引子，对应于图3(c)中的最大Lyapunov指数L1>0 。观察图3(a)可以发现，当c位于区间(16.31,16.684)∪(18.928,23.68)时系统处于周期态，而在c>23.68 时 最大Lyapunov指数L1小于零，进入稳定不动点状态。再来将目光聚焦到图3(b)中，容易发现系统随参数d变化的共存分岔轨迹与图3(a)中随参数c的变化规律呈现出对称性。参数d由1.59开始增加，系统先后经历了稳定点、倍周期分岔至混沌态、多周期、周期窗和大周期等运动状态。结合图3(d)的Lyapunov指数谱，将系统随参数c,d变化的运动状态与具体的区间分布列于表2中，直观地展现两个参数的对称共存分岔行为。

表2 振荡器随参数c, d变化时的运动状态和对应Lyapunov指数

图2 系统混沌相图

图3 共存分岔图和Lyapunov指数谱

3.2 双参数平面内的对称运动分布

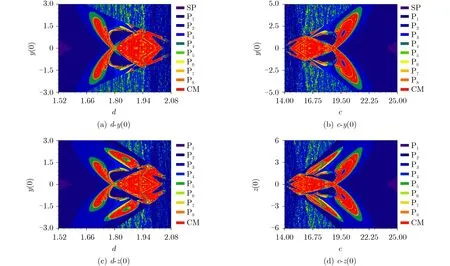
进一步探讨系统参数对运动状态对称性分布的影响，绘制对称参数和电容C的参数b以及有源磁控忆阻参数n2的双参数图如图4所示。图中不同颜色代表着不同状态的动力学行为，“SP”指的是稳定不动点(Stable point)，“P1～P8”表示的是周期1至周期8极限环(Period 1～Period 8)，“CM”则代表着混沌、多周期等复杂运动(Complex motion)。

将图4(a)，图4(b)与图4(c)，图4(d)分为两组，分别命名为组Ⅰ和组Ⅱ，容易看出同组中的动力学地图呈现对称分布。在组Ⅰ中，展现了在完整对称参数域下与参数b的运动轨迹分布。参数d从1.52递增至2.08的过程中，无论参数b取值如何，系统总是遍历稳定不动点、周期、混沌和大周期4种运动状态。相反地，当参数c∈(14.00,25.00)时，动力学行为分布先是从大周期到混沌，再过渡到周期，最终抵达稳定点。大周期状态即为组Ⅰ中类似马赛克的部分。为了更好地观察周期与混沌态的共存情况，截取了部分对称域与忆阻参数n2的组合得到组Ⅱ，消除了稳定点和大周期状态。和组Ⅰ相比，运动状态的遍历性仍保持一致，且均具有多种运动状态共存的特点。但是，组Ⅱ中忆阻参数经历由负值到正值的转变，表明忆阻元件由有源状态切换为无源状态，同时拓宽吸引域范围，系统在多周期和混沌掺杂区域中运动状态的切换更为频繁，而且随着忆阻参数的增大，多周期和混沌掺杂区的范围逐渐减小。这些都表明了将忆阻元件引入混沌振荡电路中，不仅可以保留原系统中固有的动力学行为，更能丰富其复杂的动力学现象。

图4 双参数动力学地图

3.3 依赖于对称参数的初值域内聚合费根鲍姆树现象

研究对称参数对系统中存在的反单调行为的影响，该行为主要表现为成对出现的倍周期分岔和反倍周期分岔级联现象，亦被称为聚合费根鲍姆树现象。图5(a)～图5(f)中记录不同参数d下，状态变量ymax随初始条件z(0)变化的费根鲍姆树分裂和聚合的过程。当d=1.65时，系统关于初值的对称性，使z(0)在 区间(−4,4)内，左右分岔轨迹各出现周期2气泡。在d增加至1.68后，左右周期2气泡分支上小范围内分裂出新气泡，形成周期4气泡。按此规律，继续分裂出周期8气泡。d=1.698时，周期8气泡内出现混沌域，随着d值增加，原来不接壤周期-混沌气泡开始走向聚合，形成更大范围内的周期-混沌气泡串。

为验证对称参数在初值域内的反单调现象的对称性，选择6组和图5相对应的参数c值，得到图6(a)～图6(f)中具有相同周期、混沌气泡状态的分岔轨迹图。与参数d的递增趋势不同，图6中展现的是随c值减小，在初值z(0)区间内遍历了周期2气泡→周期4气泡→周期8气泡→8周期-混沌气泡→4周期-混沌气泡→2周期-混沌气泡的气泡吞吐过程。

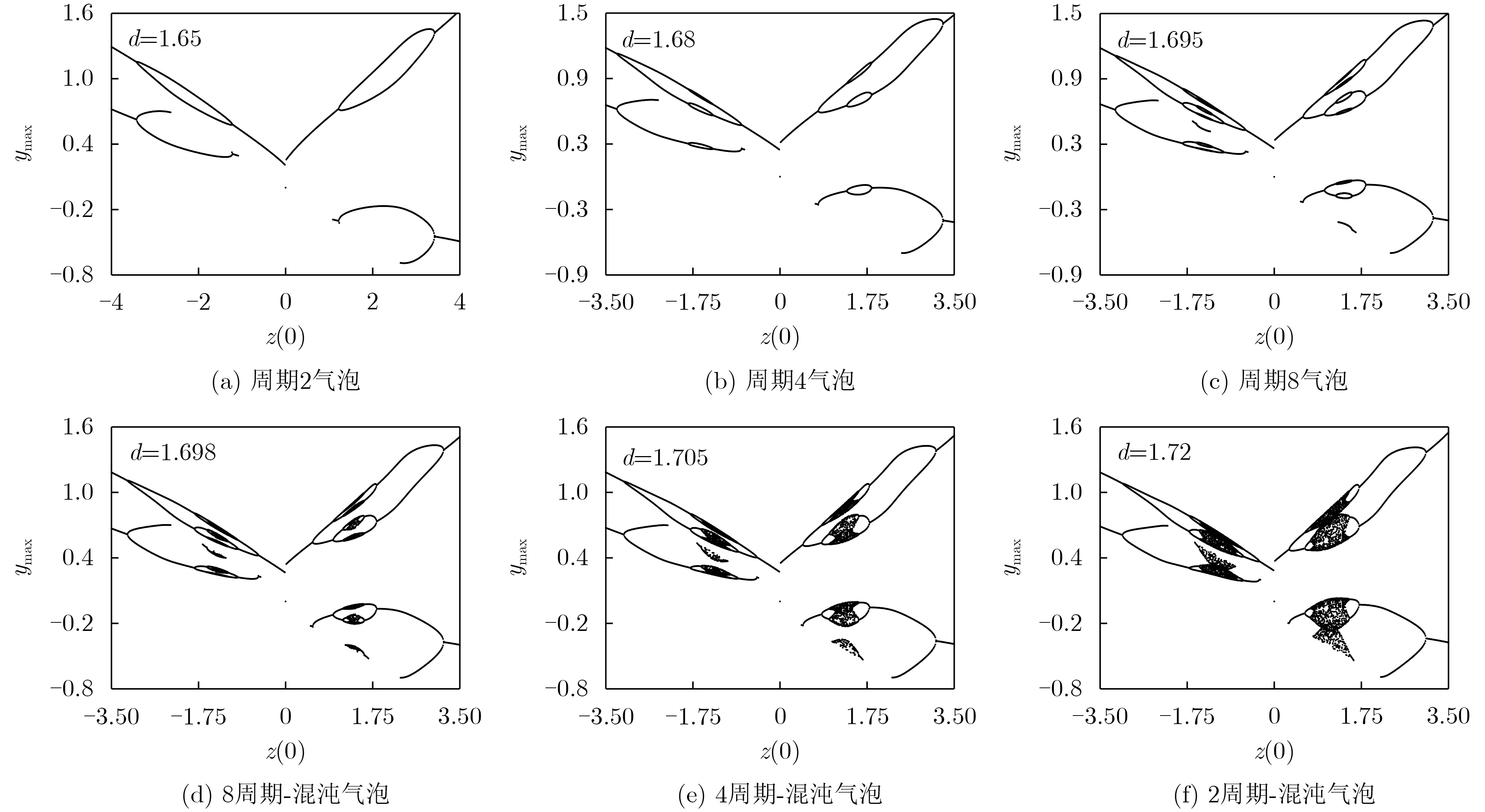
图5 对称参数d 决定的初值z (0)区间内聚合费根鲍姆树现象

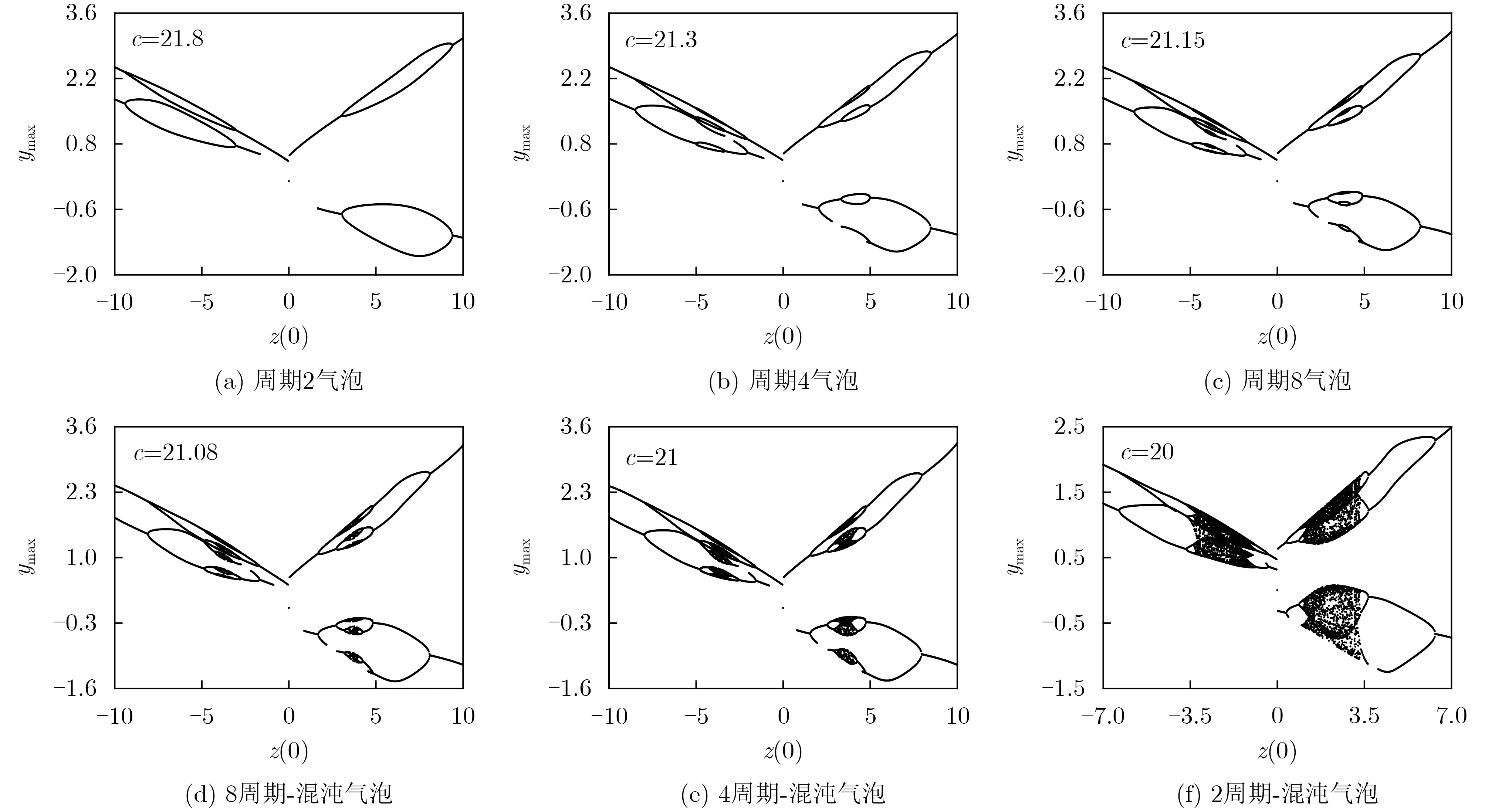
图6 对称参数c 决定的初值z (0)区间内聚合费根鲍姆树现象

3.4 忆阻初值影响下的不完全对称共存现象

分析在无源磁控忆阻初值u(0)的影响下，参数c区间内的不完全对称共存现象。选择u(0)=±0.2，参数c区间为( 15.1,21.9)时 ，得到状态变量xmax的共存分岔图和对应的前4根Lyapunov指数对比图如图7所示。图7(a)中从初始条件(10−6,10−6,10−6,0.2,0) , ( 10−6,10−6,10−6,−0.2,0) ,(−10−6,−10−6,−10−6,0.2,0) 和(−10−6,−10−6,−10−6,−0.2,0)出 发的轨迹分别被标记为红色、绿色、粉色和蓝色。

图7(a)中，红色和蓝色轨迹互为平移关系，两者在所选参数c区间内经历的吸引子状态具有一致性，从左至右依次经历混沌、反倍周期分岔、周期-混沌气泡、鞍结分岔，最终再一次反倍周期分岔从混沌走向周期1。丰富的动力学行为过程在图7(b)中初值为正的Lyapunov指数谱上表现为谱线波动频率高，系统内不断发生运动状态的切换。当初始条件中忆阻项和非忆阻项异号时，即绿色轨迹和粉色轨迹在参数区间内呈现的运动状态相同，稳定点处轨迹重合，周期态处互为平移关系。截取参数c ∈(15.1,17.1)时两轨迹对应的周期态放大图见图7(a)右下角，可以看出此时出现的是共存周期4气泡。结合图7(b)，分析得出在初值同号和异号时，振荡器在15.1

图7 参数c 区间内共存分岔图和Lyapnnov指数谱

3.5 对称域内的多稳态现象

研究在对称参数c,d影响下参数-初值域内的对称多稳态现象，数值仿真得到图8中的两组对称参数d,c分别和两个非忆阻状态变量组合的“金鱼”状吸引盆平面。参数选择见表1，图8(a)，图8(b)中初值设置为 (0,y(0),0,0,0)，类似地，图8(c)和图8(d)中为( 0,0,z(0),0,0)。

观察图8可以发现不同参数区间内的对称性由参数域延续到初值域，无论是选择参数或是初值，系统呈现出的独特对称性均取决于参数d, c。同时由于该系统自身在初值域固有的对称性，即改变状态变量的正负，系统的状态方程始终保持不变，导致图8中的多吸引子共存状态均关于初值为0的界线上下对称分布。图8中的两组图分别在“金鱼”头部分完全对称，而右半部分的图中“金鱼”翅和尾巴却活跃在更为广泛的初值区间内，分别和左半部分的两张图呈现出运动趋势的相似性。造成这种现象的原因是忆阻电路具有依赖于初值的极端敏感性，而c是动态元件电容的参数，d对应的是静态元件电阻的参数。当两参数分别渐变时，动态参数更易刺激系统在更为宽广的初值域内产生复杂的多种运动状态吸引子共存现象。

为了验证参数c,d在初值影响下的对称多稳态现象。在图8(a)，图8(b)中运动状态相同的区域，各选取3组相反初值、参数取值不同的组合，数值仿真得到了系统在y−z平面中的多种运动状态吸引子共存的相轨迹图如图9和图10所示。

图8 对称参数与初值的吸引盆

图9 参数d 和初值y (0)决定的共存相轨迹图

图10 参数c 和 初值y (0)决定的共存相轨迹图

4 基于FPGA数字技术的电路实验

考虑利用FPGA技术平台进行数字电路实验，对振荡器的数值仿真结果进行验证。不同于一般焊接电路在调节参数和设定初值上难以控制误差，FPGA平台中功能的实现主要依赖于编程，使得系统参数的更改和初值的设置更为方便精准，适用于实现对参数及初值极端敏感的忆阻混沌电路。

双忆阻Shinriki振荡器的整体程序设计分为4个模块，分别是module_DMSO, module_4RK,module_XB和module_DA模块。其中，第1个模块为顶层模块，其它3个模块为底层模块。module_DMSO作为顶层模块控制并依次调用其它3个底层模块，按顺序重复调用module_4RK和module_XB模块，module_DA模块的作用是将32位浮点数转化为定点数输出，最终在示波器上显示相应的波形图。

FPGA实验的实物连接图和不同平面上的混沌吸引子相轨迹图如图11所示。图11(b)中的混沌相图分别对应图2(a)，图2(b)中的数值仿真结果。此外，为了验证对称参数在初值域内的多稳态现象，选择图9的相轨迹图一一进行验证得到图12，参数选择和初值设定参照图9。通过FPGA数字电路实验，证明了所构双磁控忆阻Shinriki振荡器的物理可实现性，而电路实验结果和数值仿真的一致性，既证明了系统存在多运动状态吸引子共存的多稳态现象，也从侧面佐证了特殊参数下动力学行为呈现对称性分布的正确性。

图11 FPGA数字电路实验结果

图12 多稳态相轨迹图验证，CH1=200 mV, CH2=1 V

5 结论

本文利用无源磁控忆阻替换经典Shinriki振荡器中的串并联二极管支路，再将RLC谐振回路中的电阻用有源磁控忆阻取代，并在电感支路串联电阻，构造出拥有复杂电路结构的改进型双磁控忆阻Shinriki振荡器。通过观察特定参数对应的共存分岔图和李雅普诺夫指数谱，发现该振荡器中存在独特的对称分岔运动。之后通过双参数运动分布图再次验证了系统对称运动状态的存在性。在对称参数与非忆阻初值组合的吸引盆中分析了对称域中的多稳态特性，同时发现了对称域内系统的反单调性和依赖于初值的不完全对称行为。最后，基于FPGA技术对双磁控忆阻Shinriki振荡器进行了数字化实验，从示波器中观察到系统不同状态下的共存吸引子，既验证了数值仿真的正确性，也突出系统对称运动状态分布的存在性。