关于n-phantom-态射和n-Ext-phantom-态射的刻画
兰开阳,卢博
(西北民族大学数学与计算机科学学院,甘肃兰州 730030)
1 预备知识
若无特殊说明,文中所有的环R均指带单位元的结合环,所有的R-模均指幺模,即设M为左R-模,则对任意的x∈M,有1x=x,其中1 是环R中的单位元。左R-模M的示性模记为M+。设A,B为左R-模,n为正整数,Torn(A,B)和Extn(A,B) 分别指。Ab 表示阿贝尔群范畴;对于环R,R-Mod 表示左R-模范畴,Mod-R表示右R-模范畴。R-Mor 表示对象为左R-模态射、态射为左R-模态射f:M1→M2到左R-模态射g:N1→N2之间的态射范畴,即态射对的交换图:
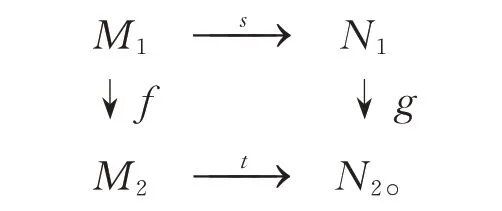
FU 等[1]提出理想逼近理论,称双边函子HomR(−,−):R-Modop×R-Mod→Ab 的子加法双边函子为范畴R-Mod 的理想,记为I。对任意2个左R-模M和N,I 中态射M→N构成一个阿贝尔群HomR(M,N),对I 中任意3 个态射f,g,h,合成fgh有意义且g∈I,则有fgh∈I。理想逼近理论将经典的覆盖与包络理论一般化[2]。如phantom-态射的理想就是范畴R-Mod 的理想。Phantom-态射的研究思想来源于拓扑学中CW-复形之间的态射[3],NEEMAN[4]首先将phantom-态射的概念应用于三角范畴并做了相关研究。HERZOG[5]将phantom-态射的定义推广至结合环范畴,并做了大量研究。
如果P1,P2是投射左R-模,且f是可裂单态射,则称范畴R-Mor 中态射f:P1→P2是投射 的;如果E1,E2是内射左R-模,且g是可裂满态射,则称范畴R-Mor 中态射g:E1→E2是内射的;如 果F1,F2是平坦左R-模,且h是纯单态射,则称范畴R-Mor 中态射h:F1→F2是平坦的[6]。
2 Torn-单态射、Extn-满态射
Phantom-态射与Ext-phantom-态射的概念最早出现在文献[5]中,下面给出Torn-单态射与Extn-满态射的定义。
定义1设n是正整数,如果对任意的(有限表示)左R-模X,有
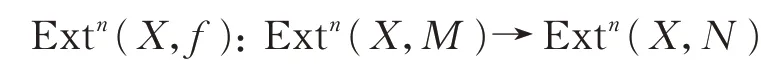
满态射,则称左R-模态射f:M→N是Extn-满态射的;如果对任意的(有限表示)右R-模Y,有
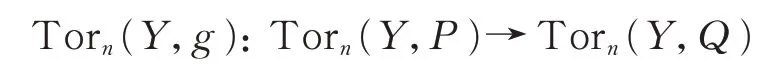
单态射,则称左R-模态射g:P→Q是Torn-单态射的。
下面的对偶定义来自文献[8]。
设n是正整数,如果对任意的(有限表示)右R-模X,有

满态射,则称左R-模态射f:M→N是Torn-满态射的;如果对任意的(有限表示)右R-模Y,有

单态射,则称左R-模态射g:P→Q是Extn-单态射的。
在文献[5]中,如果对任意的(有限表示)右R-模X,有

零态射,则称左R-模态射f:M→N是phantom-态射的;在文献[7]中,如果对任意的(有限表示)左R-模Y,有

零态射,则称左R-模态射g:P→Q是Extphantom-态射的;MAO[6]引入了n-phantom-态射和n-Ext-phantom-态射的概念,设n是正整数,如果对任意的(有限表示)右R-模X,有

零态射,则称左R-模态射f:M→N是n-phantom-态射的;如果对任意的(有限表示)左R-模Y,有

零态射,则称左R-模态射g:P→Q是n-Extphantom-态射的。
显然,R-Mod 中的1-phantom-态射恰好是phantom-态射;R-Mod 中的1-Ext-phantom-态射恰好是Ext-phantom-态射。
下面讨论n-phantom-态射与Torn-单态射以及n-Ext-phantom-态射与Extn-满态射之间的关系。
命题1设是左R-模的短正合列,则
(1)α是n-phantom-态射的当且仅当β是Torn-单态射的;
(2)β是n-Ext-phantom-态射的当且仅当α是Extn-满态射的。
证明(1)对任意的右R-模M,由短正合序列

可得正合序列

所 以,Torn(M,α)=0 当且仅当Torn(M,β)单态射,故α是n-phantom-态射的当且仅当β是Torn-单态射的。
(2)对任意的(有限表示)左R-模N,由短正合序列

可得正合序列
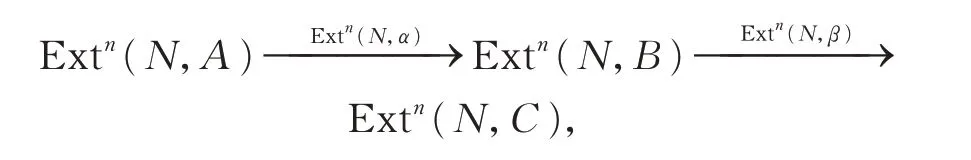
因此,Extn(N,β)=0 当且仅当Extn(N,α)是满态射的,故β是n-Ext-phantom-态射的当且仅当α是Extn-满态射的。


则
(1)f是n-Ext-phantom-态射的当且仅当h是n-Ext-phantom-态射的;
(2)f是Extn-单态射的当且仅当h是Extn-单态射的。
证明对任意的(有限表示)左R-模X,由短正合序列

可得正合序列

因为Extn(X,i)单态射,所以Extn−1(X,π)满态射。考虑行正合的交换图:
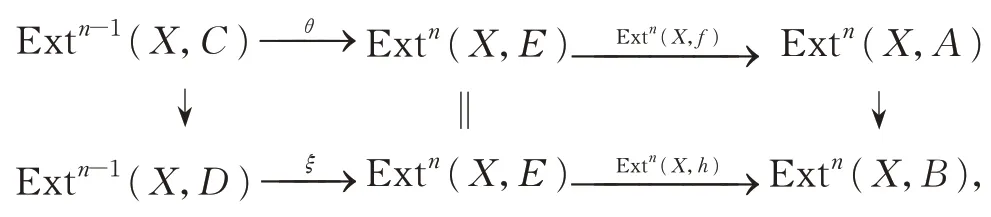
从而有
(1)f是n-Ext-phantom-态射的当且仅当θ满同态当且仅当ξ满同态当且仅当h是n-Extphantom-态射的;
(2)f是Extn-单态射的当且仅当θ=0 当且仅当ξ=0 当且仅当h是Extn-单态射的。
命题3设f,g,h是R-Mod 中态射 的,且满足fg=h。若f是Torn-单态射的,则
(1)h是n-phantom-态射的当且仅当g是nphantom-态射的;
(2)h是Torn-单态射的当且仅当g是Torn-单态射的。
证明对任意的右R-模M,有

因为Torn(M,f)单态射,所以有
(1)Torn(M,h)=0 当且仅当Torn(M,g)=0,故h是n-phantom-态射的当且仅当g是nphantom-态射的;
(2)Torn(M,h) 是单态射的当且仅当Torn(M,g)是单态射的,从而h是Torn-单态射的当且仅当g是Torn-单态射的。
命题4设f,g,h是R-Mod 中态射的,且满足fg=h。若g是Extn-满态射的,则
(1)h是n-Ext-phantom-态射的当且仅当f是n-Ext-phantom-态射的;
(2)h是Extn-满态射的当且仅当f是Extn-满态射的。
证明对任意的(有限表示)左R-模N,有
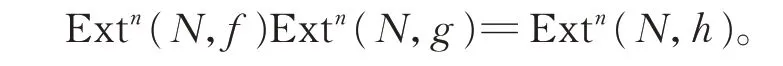
因为Extn(N,g)满态射,所以有
(1)Extn(N,h)=0 当且仅当Extn(N,f)=0,故h是n-Ext-phantom-态射的当且仅当f是n-Extphantom-态射的;
(2)Extn(N,h)满态射当且仅当Extn(N,f)满态射,从而h是Extn-满态射的当且仅当f是Extn-满态射的。
如果对任意的左R-模M,有

是正合的,则称R-Mod 中的短正合序列

是纯正合的[9],或者等价地,对任意的(有限表示)R-模N,有

是正合的,则称X是Y的纯子模,Z是Y的纯商模。
如果对每个左R-模纯正合序列

均是正合的,则称左R-模M是纯内射的。显然,每个内射左R-模都是纯内射的。
由文献[5],R-Mod 中的满态射f是Tor1-满态射的当且仅当f是纯满的;由文献[7],R-Mod 中的单态射g是Ext1-单态射的当且仅当g是纯单的。
定理1设R是一个环,则
(1)如果左R-模态射f:M→N是Torn-单态射的,则对任意的正整数m(m>n),f是Torm-单态射的;
(2)如果环R是凝聚环,且R-Mod 中的R-模态射g:P→Q是Extn-满态射的,则对任意的正整数m(m>n),g是Extm-满态射的。
证明(1)对任意的右R-模X,存在短正合列

其中,H为投射右R-模。于是可得行正合的交换图:
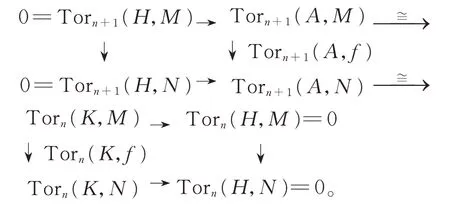
因为 Torn(K,f) 是单态射的,所以Torn+1(A,f)是单态射的,由数学归纳法,对任意的正整数m且m>n,f是Torm-单态射的。
(2)对任意的(有限表示)左R-模Y,因为R是凝聚环,所以存在短正合列

其中,F为有限生成投射左R-模,E为有限表示左R-模。于是可得行正合的交换图:

因为Extn(E,g)满态射,所以Extn+1(B,g)满态射,从而由数学归纳法,对任意的正整数m且m>n,g是Extm-满态射的。
定理2设R是一个环,则
(1)左R-模态射f:M→N是Torn-单态射的当且仅当在Mod-R中有f+:N+→M+是Extn-满态射的;
(2)如果环R是凝聚环,那么R-Mod 中的R-模态射g:P→Q是Extn-满态射的当且仅当Mod-R中的g+:Q+→P+是Torn-单态射的。
证明(1)对任意的(有限表示)右R-模X,可得交换图:

由文献[10],因θ和δ标准自然同构,所以Torn(X,f)是单态射的当且仅当Torn(X,f)+满态射当且仅当Extn(X,f+)满态射。因此,R-Mod 中的左R-模态射f:M→N是Torn-单态射的当且仅当Mod-R中的f+:N+→M+是Extn-满态射的。
(2)对任意的(有限表示)左R-模Y,可得交换图:
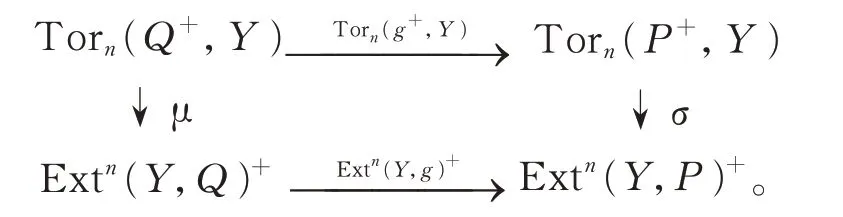
由文献[10],因μ 和σ 同构,所以Extn(Y,g)满态射当且仅当Extn(Y,g)+单态射当且仅当Torn(g+,Y)单态射。因此,R-Mod 中的R-模态射g:P→Q是Extn-满态射的当且仅当Mod-R中的g+:Q+→P+是Torn-单态射的。

