回路范畴的扩张及其应用

冯 清 ， 黄 菊 ， 郑丽红

（1.福建师范大学福清分校 电子与信息工程学院， 福建 福清 350300； 2.闽南师范大学 数学与统计学院，福建 漳州 363000； 3.福建师范大学 数学与信息学院， 福建 福州 350100； 4.列东中学，福建 三明 365000）

1968 年，Bass[1]为研究范畴 K1群结构，引入了回路范畴，并给出了一族范畴同构.2012 年，张锦州[2]给出关于K1群的一个定理，并构造出回路范畴上的一个Recollement.在此基础上，文献[3]讨论了平凡扩张范畴、冲积范畴与回路范畴的交换关系.受此启发，本文主要讨论函子范畴、推出范畴与回路范畴之间的交换关系.

1 回路范畴与函子范畴

范畴论中，研究范畴间的函子关系是研究两范畴关系的一个基本手段，函子范畴是指两个范畴间的函子所具有的范畴结构，是范畴论发展的一个重要分支.许多常见的范畴均为函子范畴，如G-集范畴，直向图范畴等等.本节讨论回路范畴与函子范畴的交换关系，并给出实例.

先给出回路范畴，函子范畴的定义，具体参见文献[1,4].

定义1[1]设D 是范畴，定义回路范畴D 如下：

定义2 设C 是小范畴，D 是范畴，定义函子范畴DC如下：

DC的对象为F：C→D 为共变函子.

DC的态射为：F→G.合成是自然变换的合成.

现给出函子范畴DC与回路范畴D 之间的关系，即

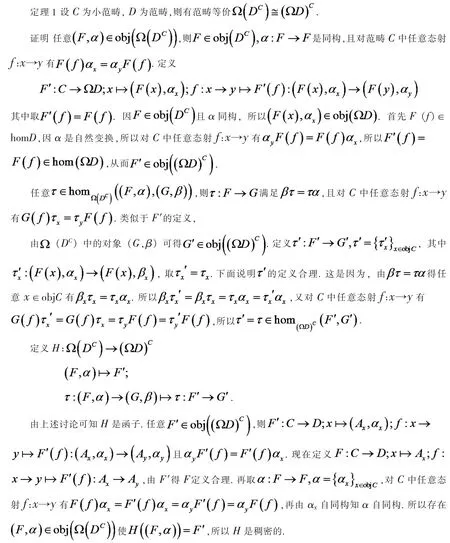
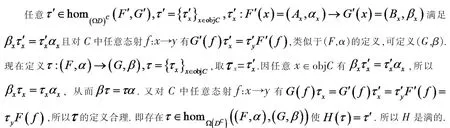
再由H 中态射的对应易知H 是忠实的.综合上述讨论知H 是等价函子， 所以有范畴等价.

现将定理1 应用于Abel 群范畴及图范畴.

例 1 设 R 是环 R 的单对象范畴， Ab 是 Abel 群范畴， R-Mod 是环 R 的左模范畴，则.其中对应关系为

图1 图范畴交换图Fig.1 The exchange graph of graph category

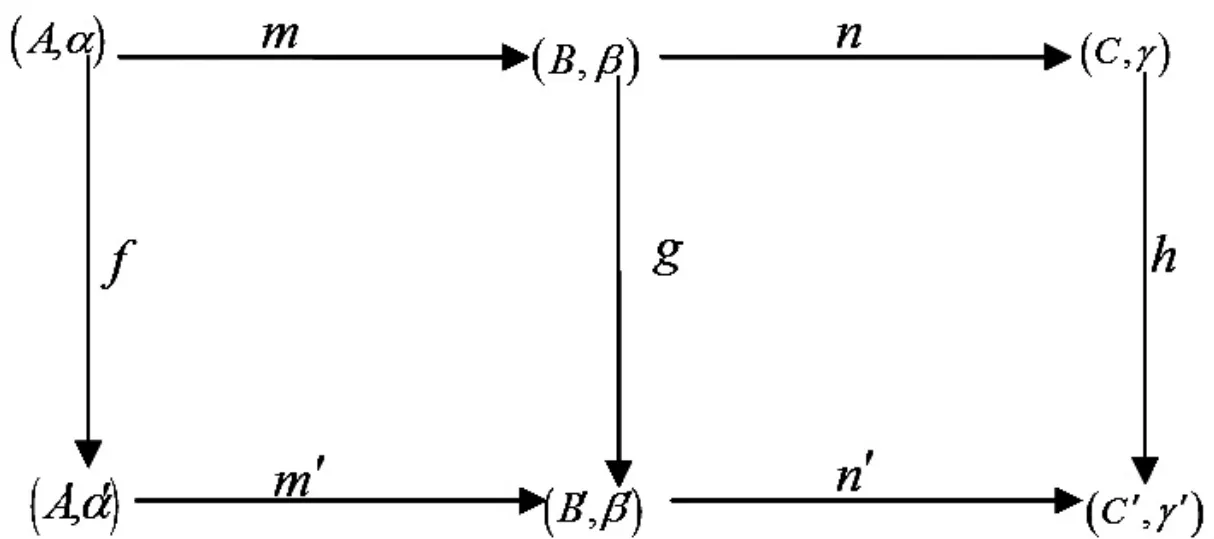
图2 回路范畴的图范畴交换图Fig.2 The exchange graph of graph category of Loop category

2 回路范畴与推出范畴

拉回与推出（纤维积与纤维余积）是范畴论中两个重要的对偶概念.沈倩芳[5]定义了推出范畴，并证明了加法范畴的推出范畴仍是加法范畴.事实上，推出范畴作为范畴的一种扩张保持原范畴的诸多同调性质.本节讨论回路范畴与推出范畴之间的交换关系.

定义5[5]设D 是范畴，以D 中的推出作为对象，推出态射作为态射构成范畴，称之为D 的推出范畴，记为DO.

现给出本节的主定理，即

图3 推出范畴交换图Fig.3 The exchange graph of push category