链刚性和剪切场对纳米棒在纳米复合体系中分布和取向的影响
李丰庆,何林李
(温州大学 数理学院 物理系,浙江 温州 325035)
由不同形状的纳米粒子组成的聚合物纳米复合材料(PNCs),因其各项性能均较纯聚合物材料有显著提高,引起了人们的极大兴趣。特别是各向异性纳米棒分散至聚合物基质中时可增强其电学、光学、磁学、机械等性能[1-4]。最大的挑战是如何确保纳米棒均匀分散于聚合物材料。计算机模拟方法对人们理解PNCs 复杂体系起了举足轻重的作用[5],同时施加剪切场也被证明是阻止纳米填料聚集的有效手段[6]。MA 等[7]用粗粒化分子动力学模拟方法研究了剪切场下PNCs 导电率的变化,发现剪切场能有效改善纳米棒的分散状态,大大提高PNCs 的导电率。GAO 等[8]发现,当向具有一定刚性的聚合物链施加剪切场时,在剪切场诱导下的高分子链更容易引导纳米粒子的分散行为。本文用分子动力学模拟(molecular dynamics simulations,MD)方法探究高分子链与纳米棒间的相互作用、链刚性、剪切场等因素对纳米棒分布和取向的影响。在弱相互作用下,纳米棒趋于聚集状态,通过调控高分子链的刚性和施加剪切场可提高纳米棒在聚合物基体中的分散程度和取向度。本文旨在探究在保留填料固有属性的前提下,剪切场在减缓或阻止纳米棒聚集中的作用,以便更好地控制纳米棒的有序排列。
1 模型与模拟方法
采用分子动力学模拟方法研究高分子链/纳米棒复合体系,模拟体系由纳米棒和线形高分子链构成。其中高分子链采用标准的珠粒弹簧模型,体系中高分子链为2 070 条,每条高分子链由10 个直径和质量分别为σ和m的单体组成。纳米棒共400 个,每个纳米棒由5 个直径和质量也为σ和m的单体组成,即单体半径Rn=0.5σ。体系中均为无量纲量。同一高分子链或纳米棒的相邻单体均通过有限伸缩非线性弹性(FENE)势相连成键:
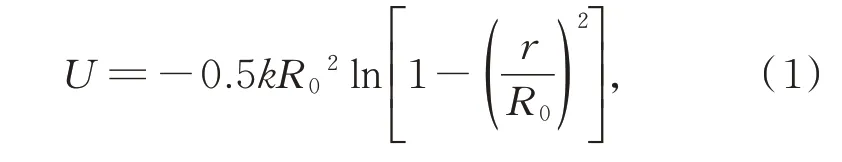
其中,k=30ε/σ2,R0=1.5σ。
高分子链或纳米棒的刚性由角度弯曲势描述[9]:
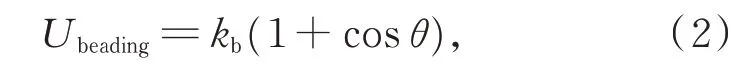
其中,θ为相邻键之间的夹角。对于纳米棒,kb=200 以确保其刚性;高分子链的刚性可通过kb值控制。本文中高分子链kb的取值范围为0~40。
为防止单体重叠,高分子链与纳米棒单体之间的相互作用由Lennard-Jones(LJ)势描述:

其中,r为任意2 个单体之间的距离,rcutoff为截断距离,C为常数。式(3)保证了势能在截断距离处是连续的。在此模拟系统中,高分子链与高分子链之间的相互作用参数和截断距离分别为εpp=1.0 和;纳米棒与纳米棒之间的相互作用参数和截断距离分别为εnn=1.0 和rnn=2.5σ;高分子链与纳米棒之间的截断距离为rnp=2.5,通过εnp调控高分子链与纳米棒间的相互作用强度。剪切率,表示剪切强度,其中最大速度vZ出现在x=0 和x=L处,最小速度vZ出现在x=L/2 处。本模拟中,约化单位ε=1,σ=1,m=1 和τ0=分别为能量、长度、质量和时间单位。
将所有高分子链和纳米棒放置于边长为L=30σ的立方体盒子中,其对应的聚合物熔体粒子数密度为ρ*=0.85σ−3。在模拟过程中,向3 个方向均施加周期性边界条件,并用正则系统进行分子动力学模拟实验,其中郎之万热浴温度固定为T*=1.0,以ε/kb为单位。用熟知的Velocity-Verlet 算法积分运动方程,所有模拟数据均为通过足够长时间的大量样本统计得到的统计平均值,其中时间步长为δt=0.005τ0,时间单位为。每个程序至少运行200 万步,系统于前150 万步达到平衡。在确保系统达到平衡状态后,后50 万步按每5 万步进行抽样统计。模拟工作均在基于分子动力学方法的LAMMPS[10]平台上展开。
2 结构与讨论
2.1 高分子链与纳米棒的相互作用强度对纳米棒分散的影响
在该模拟体系中,高分子链与纳米棒相互吸引,用参数εnp表示高分子链与纳米棒之间的吸引强度,在不同εnp下,纳米棒在聚合物熔体中表现出不同的聚集与分散行为。模拟系统中有400 个纳米棒,用纳米棒间的径向分布函数(RDF)表征聚集与分散状态。将高分子链与纳米棒间的相互作用从εnp=0.5 提高至εnp=20.0,同时保持其他参数不变。如图1(a)所示,在弱相互作用下,如当εnp=0.5 时,在r=1σ处出现一个峰(其中σ为单体直径),表明纳米棒间为直接接触的聚集状态,此时纳米棒与高分子链发生了宏观相分离。随着相互作用强度的增加,如当εnp=2.5 时,RDF 曲线未出现峰值,说明纳米棒均匀分散于聚合物基体。随着相互作用强度的进一步提高,如当εnp=10.0 时,RDF 曲线在r=2σ和r=3σ附近出现微小峰值,说明纳米棒呈现“桥接”的聚集状态,即纳米棒间隔了1 或2 条高分子链。图1(b)为在不同相互作用强度εnp下,对应纳米棒在聚合物熔体中的分布情况。在弱相互作用下,观察到纳米棒和聚合物是分离的;在中等相互作用下,纳米棒均匀分散;在强相互作用下,纳米棒间以“桥接”的方式聚集。为进一步说明纳米棒分散状态随高分子链与纳米棒间相互作用强度εnp的变化,对每个纳米棒在r=1.1σ范围内的其他纳米棒珠子数N进行了统计,统计曲线同样反映了纳米棒在熔体中的3 种典型状态:直接接触聚集、分散、“桥接”聚集。其中在中等相互作用强度(εnp=2.5)下,纳米棒处于最佳分散状态,如图1(c)所示。纳米棒周围聚合物链的径向分布函数gnp(r)如图1(d)所示。在弱相互作用下,当εnp=0.5 时,gnp(r)曲线平缓且值较小,说明纳米棒周围高分子链分布较少,纳米棒发生聚集。当εnp=2.5 时,gnp(r)曲线在r=1σ处有峰值,说明纳米棒周围优先分布高分子链。当εnp=10.0 时,gnp(r)曲线在r=1σ,r=2σ和r=3σ附近有明显峰值,说明此时高分子链缠绕在纳米棒周围形成了紧密的“桥接”聚集。
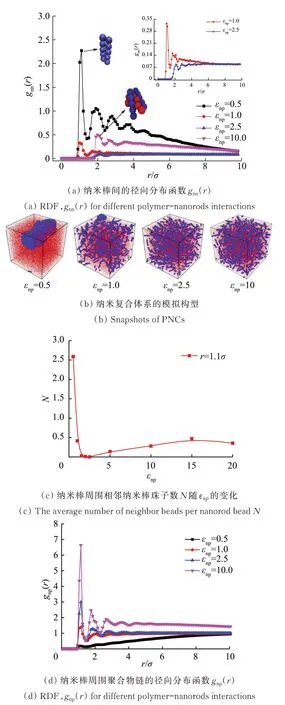
图1 纳米复合体系的模拟构图及纳米棒的分布状态统计Fig.1 Snapshots of PNC's and the statistics of the distribution state of nanorods
2.2 高分子链刚性与剪切场对纳米棒分散的影响
当高分子链与纳米棒间的相互作用较弱时,纳米棒间呈直接接触的聚集状态,不利于纳米复合材料力学性能的改善。下面将研究高分子链刚性kb对纳米棒分散程度的影响。
如图2(a)所示,当εnp=0.5 时,径向分布函数gnn(r)峰值位于r=1σ处,即纳米棒处于直接接触聚集状态。随着链刚性kb的增加,曲线在r=1σ附近的峰值略有下降。说明随着链刚性的增加,链间排斥体积效应增大,导致纳米棒间的聚集程度逐渐下降。图2(b)呈现的为纳米棒周围相邻纳米棒珠子数N随kb的变化。由图2(b)可知,随着kb的增加,纳米棒聚集体分散为小的聚集体,但仍无法达到理想的分散状态。
施加外部剪切场通常被认为是改善纳米棒分散状态的有效手段。以εnp=0.5 为例,对体系中高分子链施加z方向的剪切场,观察提高剪切率后纳米棒的空间分布。图2(c)呈现的为当kb=0 时,纳米棒周围相邻纳米棒珠子数N随剪切率的变化当较小时,纳米棒表现为直接接触聚集状态。当增大到一定值时,纳米棒分散良好。在强剪切场作用下,高分子链类似于活性剂,黏附在纳米棒表面,带动纳米棒运动。如当=0.05 时,纳米棒由直接接触聚集状态转变为分散状态;当足够大时,在连续剪切场作用下,纳米棒团簇一旦被分散就很难聚集成新的团簇。为更清晰地表示纳米棒的分散情况,分别绘制了当剪切率=0,0.020,0.035,0.060 时N随kb的变化曲线,如图2(d)所示。从图2(d)中可明显看出,在不同的剪切场强度下,聚合物链刚性的增加对纳米棒的分散有不同影响。当剪切率=0.020和0.035 时,在剪切场作用下纳米棒的分散程度随kb的变化较=0 时更明显,随着kb的增大,纳米棒的分散程度迅速增强,且在kb≥30 时,纳米棒基本达到较好的分散状态。当=0.060 时,纳米棒已处于较好的分散状态,此时与高分子链的刚性无关。这些结果证实了剪切场具有重要作用,有利于促进纳米棒分散。
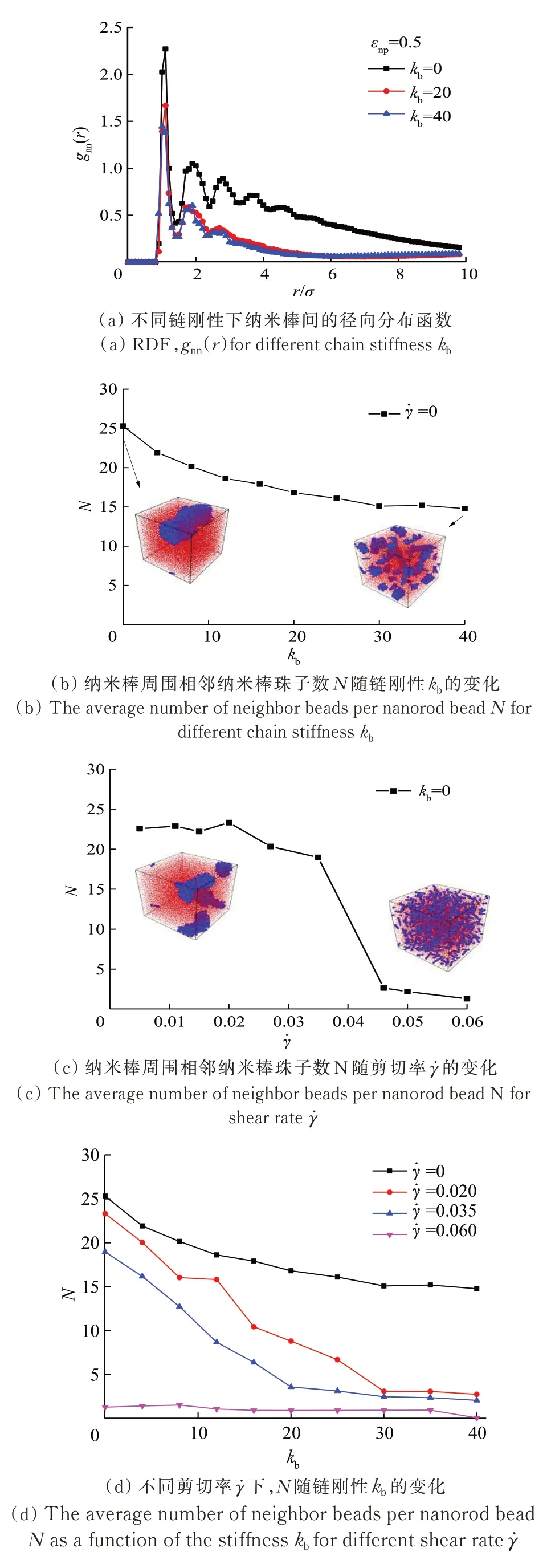
图2 纳米棒的分布和取向随链刚性和剪切率的变化Fig.2 The distribution and orientation of nanorods for chain stiffness kb and shear rate γ̇
2.3 高分子链刚性与剪切场对纳米棒取向度的影响
在纳米复合材料的制备过程中,若填料为各向异性的纳米颗粒,则不仅要求填料在熔体中均匀分散,而且颗粒排列的取向性对复合材料的性能也有很大影响。为探究高分子链的刚性和剪切场是如何诱导纳米棒的取向行为的,引入了二阶勒让德多项P2(cosθ)[11],并将其作为表征剪切过程中纳米棒取向有序度的参数:
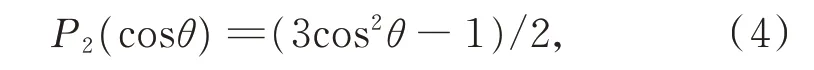
其中,θ表示纳米棒的键矢量与剪切场方向之间的夹角。当P2(cosθ)越接近1.0 时,纳米棒的取向与剪切场方向越一致。计算结果如图3 所示,在弱剪切率下,纳米棒的取向是无序的;当̇>0.015 时,纳米棒取向度迅速提高;当̇=0.035 时,P2(cosθ)接近1.0,纳米棒基本沿剪切场方向排列;随着的进一步增大,P2(cosθ)开始下降。在弱剪切率下,纳米棒聚集且取向无序,剪切率越强,高分子链在剪切场作用下的拉伸幅度越大。由于纳米棒与高分子链之间存在相互作用,在适当强度的剪切场作用下,高分子链的拉伸方向与剪切场方向一致,从而诱导纳米棒有序排列。从图3 的插图中可看出,此时纳米棒聚集成柱状,有较高的取向度。在强剪切率(̇>0.035)下,纳米棒的取向度受强烈拉伸的高分子链干扰,聚集体开始分散,导致P2(cosθ)下降。
同时考虑链刚性和剪切场对纳米棒取向度的影响。选定kb=20,并向体系施加剪切场。图4 为纳米棒取向度(左轴)和纳米棒周围相邻纳米棒珠子数N(右轴)随剪切率̇的变化。从图4 的插图中可看出,当̇=0.02 时,纳米棒具有较高的取向度,但仍处于聚集状态。当̇增至0.035 时,纳米棒的分散状态有了很大提高,即图中红色曲线N值较小,说明纳米棒均匀分散于聚合物熔体,且仍然保持较高的取向度。当进一步增大时,纳米棒的取向度又开始显著下降且保持较好的分散状态,说明剪切场强度超过临界值后,高分子链失去诱导纳米棒向列转化的能力。显然,平衡高分子链的刚性与剪切场强度是提高纳米棒取向度和分散程度的关键。随着剪切率的不断增强,半刚性的高分子链被不同程度地拉伸,对纳米棒造成不同程度的干扰。半刚性高分子链较柔性链具有更规则的拓扑结构,在同等剪切率下对纳米棒的干扰也相对较强。正如图3(b)中插图所示,在中等剪切强度下,半刚性高分子链的拉伸刚好使纳米棒分散,且此时纳米棒的取向度依然较高,高分子链诱导纳米棒取向分布达到了平衡。当高分子链与纳米棒相互作用较弱时,通过调节高分子链刚性和剪切场强度,使得原本聚集的纳米棒均匀且有序地排列在聚合物熔体中,获得取向度高且均匀分散的纳米棒复合体系,从而提高纳米复合体系的各项性能。
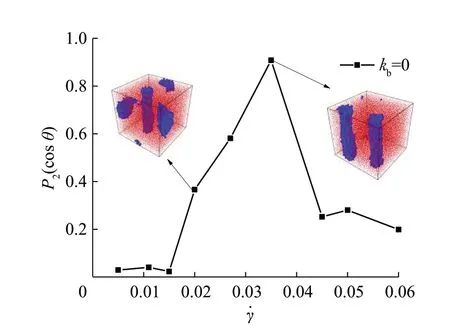
图3 当kb=0 时,纳米棒的取向度随剪切率的变化Fig.3 The order parameter P2(cos θ)as a function of the shear rate for kb=0

图4 当kb=20 时,纳米棒取向度(左轴)和纳米棒周围相邻纳米棒珠子数N(右轴)随剪切率的变化Fig.4 The order parameter P2(cos θ)(left axis)and the average number of neighbor beads per nanorod bead N(right axis)as a function of the shear rate
3 结论
采用分子动力学模拟方法研究了纳米棒在聚合物熔体中的分布与取向行为。当高分子链与纳米棒间的相互作用较弱时,纳米棒自然地呈现直接接触聚集状态。为提高纳米棒在高分子链中的分散程度和有序取向度,实验探究了高分子链刚性和剪切场的诱导作用。随着高分子链刚性的增大,纳米棒间的分散程度略有提高,即从大的聚集体分散为小的聚集体。剪切场显著影响纳米棒的分散程度,当向柔性高分子链体系施加剪切场时,纳米棒的分散程度随剪切率的增强明显提高;当向kb=20 的半刚性高分子链施加剪切场时,纳米棒的分散度与取向度很大程度上取决于剪切场强度与链刚性的协同作用。随着剪切率的增大,纳米棒的取向度先升高再下降。同时纳米棒先分散再聚集再向分散转变。尤其在=0.035 时,纳米棒的分散程度和取向程度均较高,表明通过调节高分子链刚性与剪切场强度可诱导纳米棒均匀分散和有序排列。处理好剪切场强度与高分子链刚性之间的协同关系是本研究的关键,在无须修饰纳米棒表面特性的前提下,可引导纳米棒在聚合物基体中呈现高分散度和高取向度。本研究为工业制造中材料的设计提供了新的思路。

