具有一般关联结构母子公司担保债券的定价和风险分析
林建伟,宋丽平
(莆田学院 数学与金融学院,福建 莆田 351100)
随着债券市场的发展,信用等级较低的公司通过第三方担保、母公司为子公司担保、债券保险以及信用准备金等增信方式提高其信用等级,其中母公司同时为旗下多家子公司担保的方式尤为常见。例如:2018 年4 月,杭州海康威视数字技术股份有限公司宣布为旗下17 家子公司债券提供担保,担保额度达224.50 亿元;2018 年10 月,阳光城宣布为旗下7家子公司债券提供担保,担保额度达52.98 亿元;2018 年11 月,中南建设集团股份有限公司宣布为旗下24 家子公司债券提供担保,担保额度达143.40 亿元。子公司债券获得母公司担保有助于增强子公司到期还本付息的能力,提高子公司债券的信用等级,降低子公司的融资成本,从而解决子公司融资难的问题。但同时应意识到母公司为子公司债券提供担保所隐含的违约传染性风险,即子公司的违约可能增加母公司的违约概率,或直接导致母公司违约,因此在一家母公司为n家子公司债券提供担保时,建立合理的公司债券定价模型是研究热点。
JARROW 等[1]首次通过违约强度传染模型描述了关联公司之间的违约依赖性结构,并对具有单向违约传染结构的2 家关联公司债券进行定价;COLLIN-DUFRESNE 等[2]采用测度变换方法,研究了具有环形违约传染结构的2 家关联公司债券定价问题;白云芬等[3]通过测度变换方法,研究了具有双曲衰减违约强度传染结构的2 家关联公司债券定价问题;FAN[4]采用总的违约强度构建方法,对具有环形违约传染结构的3 家关联公司债券进行定价。以上研究主要基于利率为常数的假设,讨论无担保关联公司债券定价问题。
在担保债券定价问题上,任学敏等[5]在随机利率服从Vasicek 模型下,采用约化方法对在第三方担保下的公司债券进行了定价,但模型忽略了担保所引起的违约传染性。林建伟等[6]通过环形违约强度传染模型刻画了2 家公司之间由于互相担保所引起的违约传染性,采用总的违约强度构建法考虑了双方互相担保公司债券定价问题,但模型未考虑随机利率风险的影响。夏鑫等[7]基于随机利率服从CIR模型,通过单向指数衰减违约传染模型描述了2 家公司之间因具有担保所引起的违约传染性,采用测度变换方法考虑了单方担保债券的定价问题,但模型仅获得了定价的积分表达式。近年来,杨招军等[8]采用均衡定价理论,考虑了在混合担保下企业的最优资本结构和混合担保成本的定价问题。蒋和胜等[9]实证研究了资产支持证券和资产担保债券对银行信贷的影响,认为资产担保债券具有较高的信用评级,有助于银行降低资金成本。李恩来[10]采用计量经济学方法,实证研究了担保增信措施对公司债券的作用和影响,结果表明,担保增信措施提高了公司债券的信用等级,扩大了融资规模,降低了公司债券的发行利差。江源[11]实证检验了担保增信措施对城投债信用评级和发行价格的影响关系,发现担保增信措施提高了城投债的信用等级,但对城投债发行利差无显著影响。综上,现有研究未考虑随机利率风险的影响和担保所引起的违约传染性风险[8-11]。此外,只考虑在单方担保下的公司债券定价问题[5-11],而未考虑同时为n家关联公司提供担保时的公司债券定价问题。
本文拟在随机利率服从CIR 模型[12]下,采用约化方法,考虑具有一般关联结构母子公司担保债券的定价问题。基于n+1 家公司违约强度传染性模型,刻画由一家母公司同时为n家子公司提供担保而形成的公司违约相互依赖性,采用随机分析理论,建立具有一般关联结构母子公司担保债券的数学模型,得到相应子公司债券定价的显式表达式和母公司的违约概率,并分析了定价中所蕴含的随机利率风险和因母子公司担保而产生的违约传染性风险。
1 母子公司担保债券定价
1.1 模型假设
(1)设(Ω,F,Q)表示完备概率测度空间,其中Ω 为样本空间,F是Ω 上的σ-代数,Q为(Ω,F)上的等价鞅 测度[13]。{F}0≤t≤T表示F的 一个子σ-代数流,且FT=F。rt表示随机利率过程,Fr,t=σ(rs:s≤t)为其产生的自然流。τi(i=1,2,…,n)表示子公司i的违约时间,τn+1为母公司的违约时间,Ni,t=I{τi≤t}为子公司i的违约过程,Nn+1,t=I{τn+1≤t}为 母公司的违约过程,且母公司和子公司的违约过程均独立于随机利率过程rt,以及n家子公司的违约过程两两之间相互独立。设Fi,t=σ(Ni,s:s≤t),i=1,2,…,n,n+1 表示母公司和子公司产生的自然流,Ft=Fr,t∨F1,t∨F2,t∨…∨Fn,t∨Fn+1,t表示[0,t]内市场产生的所有信息。λi,t表示随机时间τi(i=1,2,…,n,n+1)内一个非负Ft可测的违约强度过程,且在等价鞅测度Q下,对任何t≥0,数学期望和补偿过程Mi,t=Ni,t−是一个Ft可测鞅。
(2)在等价鞅测度Q下,随机利率过程rt演化服从CIR[12]模型:
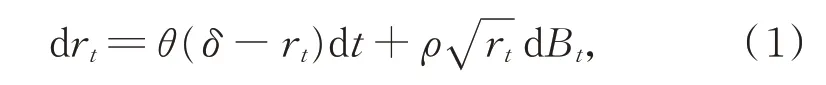
其中,θ,δ,ρ为常数,且满足2θδ≥ρ2,{Bt}t≥0为标准布朗运动。
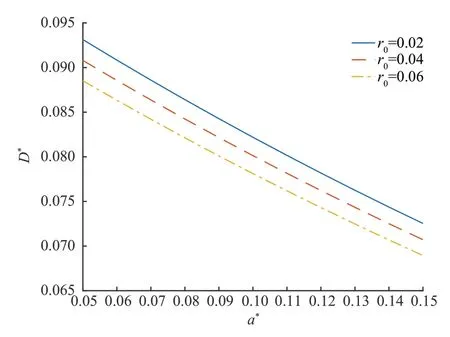
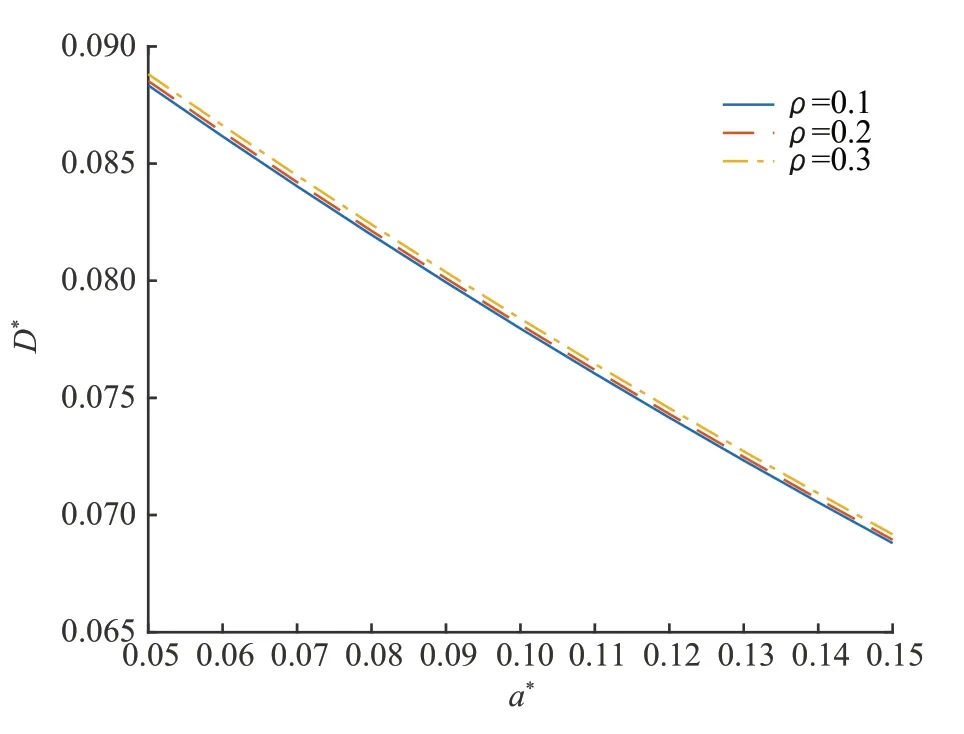
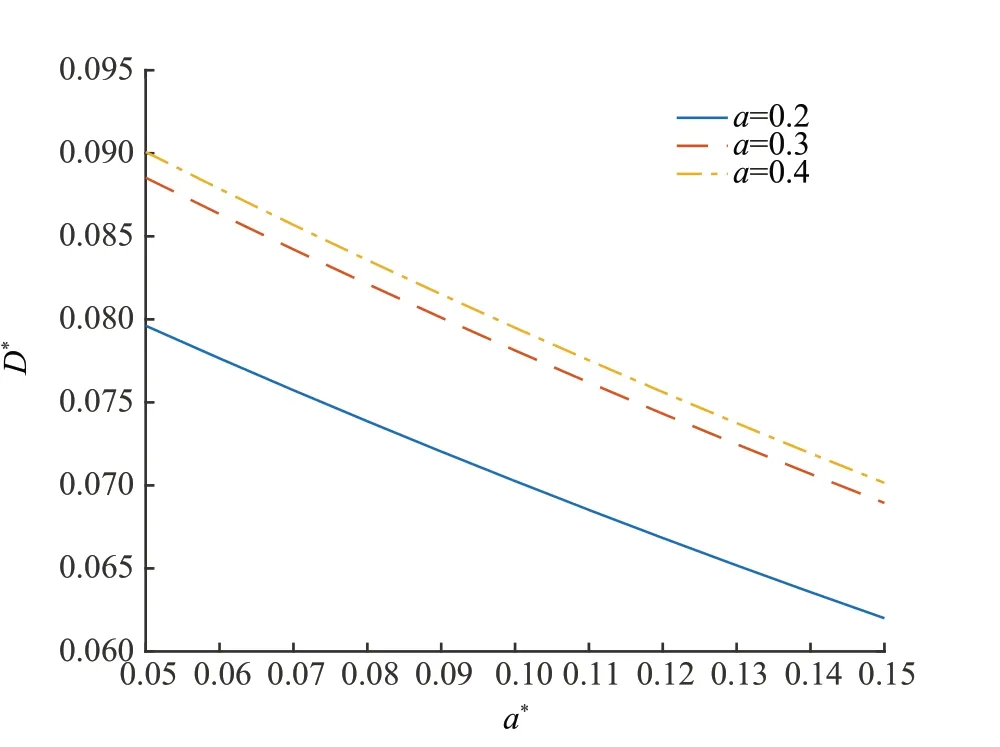
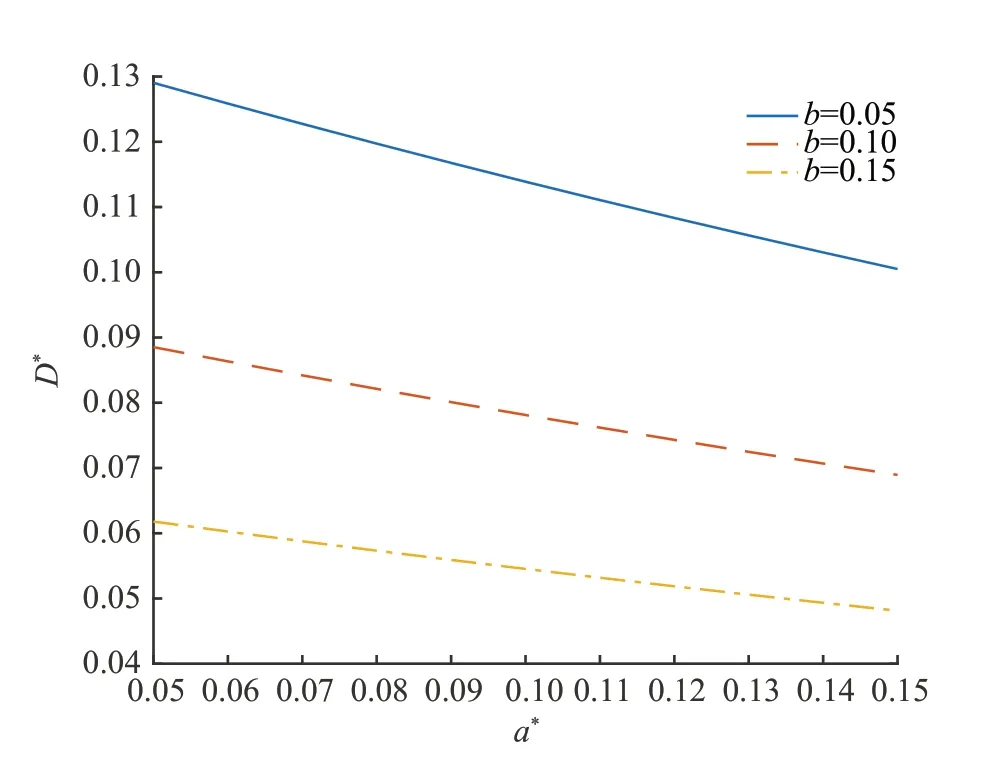
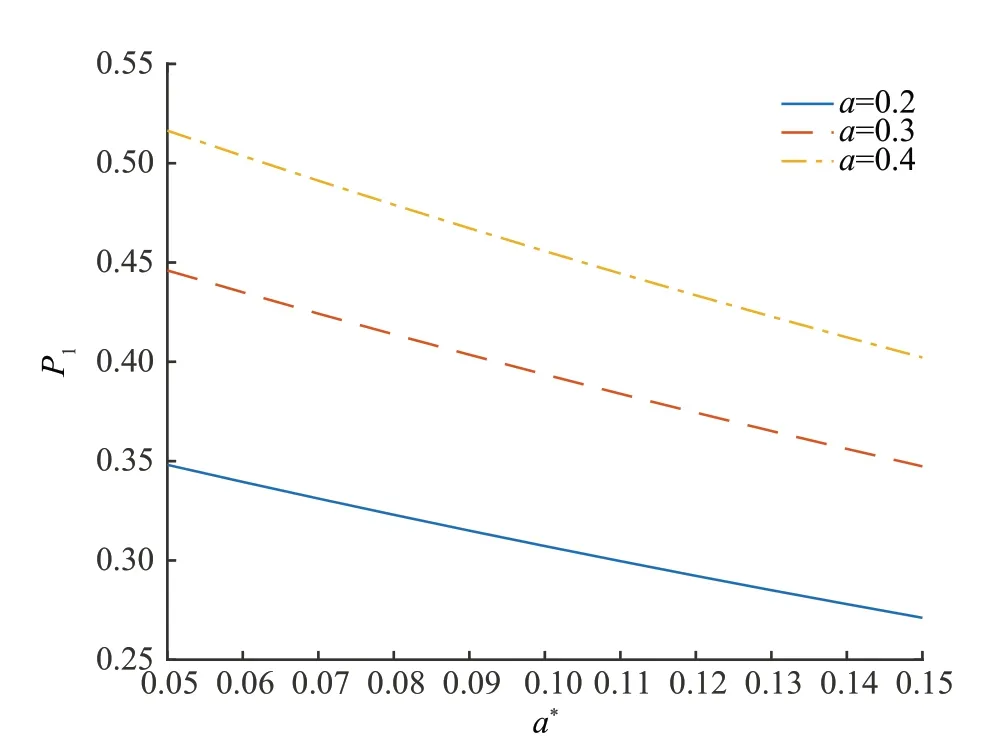
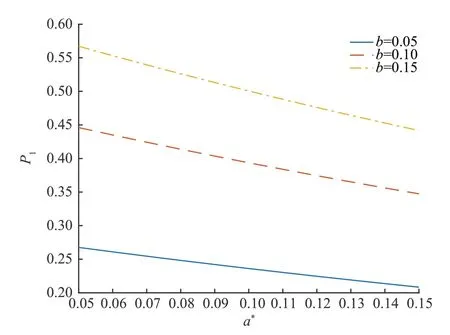
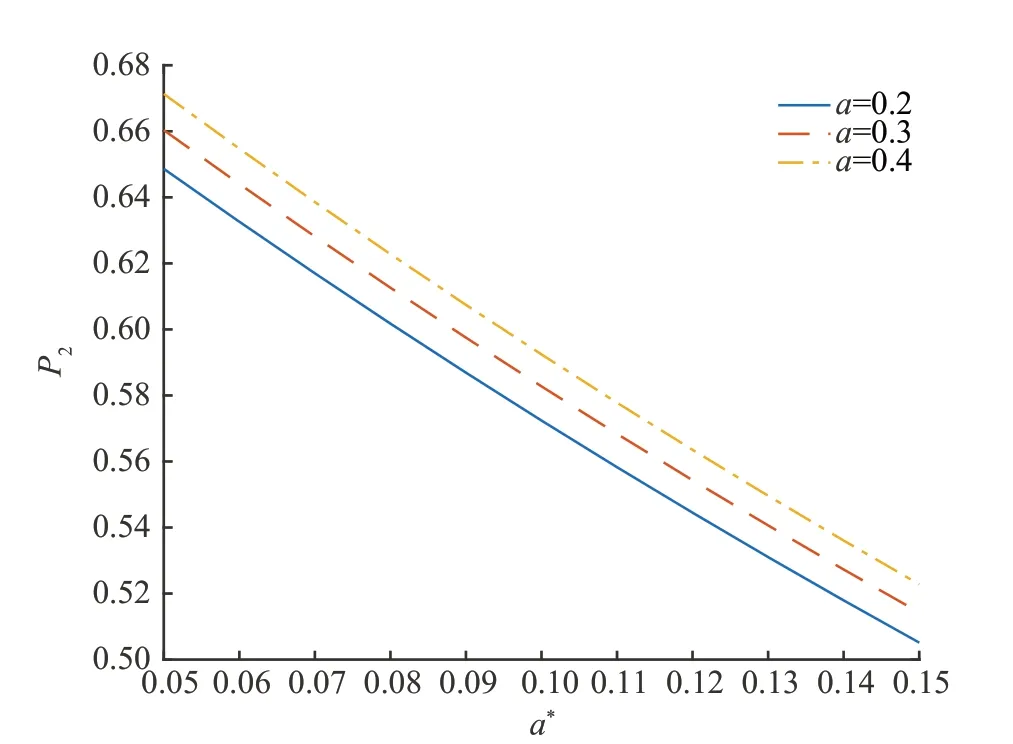
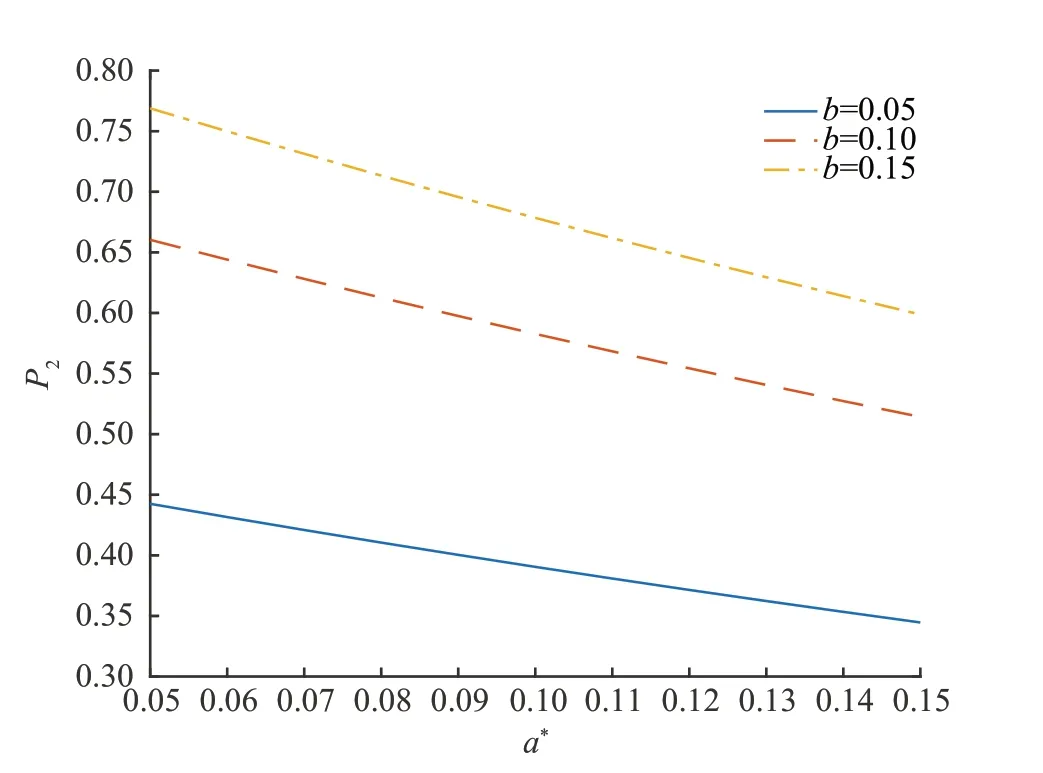
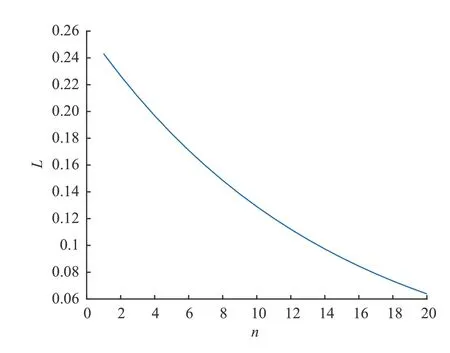
(3)设n家子公司同时发行了零息票债券,到期日为T,在债券期限[0,T]内,母公司同时为n家子公司债券提供担保,任一家子公司i在债券期限内一旦发生违约,若母公司在债券期限内没有发生违约,则子公司i的债券损失将由母公司承担,债券持有者在到期日获得1 元;若母公司在债券期限内也发生违约,子公司i的债券持有者只能在到期日得到R元,0 (4)母子公司违约强度传染性模型为 该模型刻画了一家母公司同时为n家子公司债券提供担保而形成的违约依赖性结构,侧重于母公司与子公司的差异性,而未区分n家子公司的差异性。a,a*均为正常数,分别表示子公司和母公司的自身违约因子;b为正常数,且a>b,表示因母公司为子公司i债券提供担保而形成的违约传染因子,即子公司i一旦违约,若母公司没有违约,因母公司为子公司i债券提供担保,其违约强度将发生跳跃,从a*增至a*+b。 注1条件a>b体现了由子公司i全部债务引起的违约影响程度大于仅由子公司i债券损失所造成母公司的违约影响程度。 (5)任意两家公司同时发生违约的概率为零。 由于不区分n家子公司之间的差异性,n家子公司所发行担保债券具有相同价值,因此以子公司1所发行担保债券定价为主。根据模型假设(1)~(5),在随机利率背景下具有一般关联结构母子公司担保债券定价的数学模型为 其中,D(0,T)表示子公司1 所发行的担保债券价格,式(3)右边括号内第1 项表示若子公司1 在担保债券期限内未发生违约,则债券持有者可在到期日获得1 元;第2 项表示若子公司1 在债券期限内已经违约,而母公司在债券期限内未发生违约,根据母子公司担保合约规定,母公司将承担子公司1 因发生违约而造成的损失,担保债券持有者仍将在到期日获得1 元;第3 项表示若子公司1 在债券期限内已经违约,且母公司在债券期限内也发生违约,则担保债券持有者只能在到期日获得R元。 基于式(3),结合COX 等[12]关于随机贴现因子的结果,可得母子公司担保债券价格。 定理1任意给定正数a,a*,b,满足a>b,母子公司担保债券价格D(0,T)的显式表达式为 证明基于式(3),结合随机利率r与违约时间(τ1,τ2,…,τn+1)的独立性,有 下面求解EQ(I{τ1≤T}I{τn+1 对任意k=1,2,…,n−2, 同理,可得 由此可得 综上,可求得式(4)。证毕! 在无担保情形下,母子公司违约强度的数学模型为 子公司1 债券定价的数学模型为 经计算,无担保情形下子公司1 的债券定价公式为 母公司为子公司债券提供担保所产生的价值体现在有担保与无担保2 种情形下子公司发行债券的价差,即子公司债券担保价值D*=D(0,T)−(0,T),由式(4)和式(8),可得 定理2任意给定正数a,a*,b,满足a>b,母公司担保下D*的表达式为 且D*>0。 证明由式(4)和式(8),易求得D*。由式(3),结合λ1,t==a,有 (0,T),因此,D*>0。 注2D*>0 表明母公司为子公司发行债券提供担保增大了子公司债券的发行价值,提升了子公司的信用等级,降低了子公司的融资成本,一定程度上克服了子公司融资难问题。 根据母子公司担保合约规定,一家母公司承担n家子公司可能发生违约所造成的债务损失,从而引发违约传染风险,导致母公司违约概率大大增加。设Prob(τn+1 定理3任意给定正数a,a*,b,满足a>b,P1,P2的表达式分别为 证明由式(6)可得 由式(2),并考虑n家子公司的对称性,有 对任意k=1,2,…,n−1,有 同理可得, 综上,可得P1的表达式(10)。证毕! 下面推导P2的表达式。 以及Prob(τ1 可求得 根据有担保和无担保情形下n+1 家母子公司的违约强度模型(2)和(6),可知 即P2≥P1≥0。 注3P2≥P1≥0,表明母公司为n家子公司同时提供担保,一方面,提高了子公司债券的价值,提升了子公司的信用等级;另一方面,由于母公司承担子公司违约的风险,可能引发违约传染,并增大母公司违约风险,特别在子公司肯定在到期日之前违约条件下,母公司违约概率增大幅度将是巨大的。 基于式(9)~式(11),考查随机利率风险和母公司担保对子公司债券定价的影响。基本参数设定为a=0.3,a*=0.1,b=0.1,θ=0.6,δ=0.1,ρ=0.2,r0=0.06,n=10,R=0.5,T=2.5。 图1 和图2 分别为母公司为子公司债券担保所体现价值关于初始市场利率r0和随机利率波动率ρ的依赖关系。可知,担保价值D*恒为正,且随r0和母公司的自身违约因子a*的增大而减小,随ρ的增大而增大。其蕴含的金融意义为:(1)母公司担保增强了子公司到期还本付息的能力,提升了子公司信用等级,由此提升了子公司债券的发行价值;同时母公司的信用等级越高,其为子公司债券担保所体现的价值越大;(2)市场经济越不景气,市场环境波动越大,母公司为子公司债券担保所体现的价值越大。 图1 担保价值D*关于a*和r0 的变化关系Fig.1 The guarantee value D* with varying a* and r0 图2 担保价值D*关于a*和ρ 的变化关系Fig.2 The guarantee value D* with varying a* and ρ 图3 和图4 分别为母公司的担保价值D*关于子公司自身违约因子a和违约传染因子b的依赖关系。可知,担保价值D*随子公司自身违约因子a的增大而增大,随违约传染因子b的增大而减小。其蕴含的金融意义为:子公司的信用等级越低,母公司的信用增级作用越明显,相应地,母公司的担保价值越大;但当子公司违约对于母公司造成的违约传染程度越严重时,母公司担保对于增强子公司到期还款付息能力减弱,从而降低母公司的担保价值。 图3 担保价值D*关于a*和a 的变化关系Fig.3 The guarantee value D* with varying a* and a 图4 担保价值D*关于a*和b 的变化关系Fig.4 The guarantee value D* with varying a* and b 图5 和图6 分别为母公司违约概率增大幅度P1关于子公司自身违约因子a和违约传染因子b的依赖关系。可知,相比于无担保情形,担保情形下母公司在到期日之前违约概率增大幅度恒为正,且其随子公司自身违约因子a和违约传染因子b的增大而增大。其蕴含的金融意义为:在债券到期日之前,若子公司发生违约,因母公司同时为n家子公司发行的债券提供担保,承担子公司违约所造成的债务损失,致使母公司的违约强度发生跳跃,可能由b增至nb,因此增大了母公司的违约概率,即P1恒为正,同时当子公司自身违约因子a和违约传染因子b增大时,均造成违约传染程度加剧,P1更大,特别是当b=0.15 时,P1最大值约为0.57。 图5 违约概率增大幅度P1 关于a*和a 的变化关系Fig.5 The increasing range of default probability P1 with varying a* and a 图6 违约概率增大幅度P1 关于a*和b 的变化关系Fig.6 The increasing range of default probability P1 with varying a* and b 图7 和图8 分别为母公司条件违约概率增大幅度P2关于子公司自身违约因子a和违约传染因子b的依赖关系,进一步表明,在n家子公司于到期日之前肯定违约条件下,母公司由于为子公司担保而引发的违约传染程度进一步扩大,P2更大,特别是当b=0.15 时,P2最大值约为0.77。这也蕴含了母公司担保虽然可使子公司信用增级,但也可能引发巨大的违约传染风险。 图7 条件违约概率增大幅度P2 关于a*和a 的变化关系Fig.7 The increasing range of conditional default probability P2 with varying a* and a 图8 条件违约概率增大幅度P2 关于a*和b 的变化关系Fig.8 The increasing range of conditional default probability P2 with varying a* and b 图9 子公司债券价值增长率L 关于n 的变化关系Fig.9 The increasing ratio of the subsidiary bond value L with varying n 图10 母公司违约概率增长率Q 关于n 的变化关系Fig.10 The increasing ratio of parent company default probability Q with varying n 综合采用随机分析理论和约化方法,在随机利率服从CIR 模型背景下,基于一家母公司和n家子公司的违约强度传染模型,刻画了母公司为n家子公司债券提供担保所形成的违约相关性,建立了具有一般关联结构母子公司担保债券定价的数学模型,得到母子公司担保债券解的闭合表达式。相比于无担保情形,进一步获得了母公司为子公司担保所体现的担保价值和可能引发的母公司违约概率增大幅度的显式表达式。围绕担保价值和母公司违约概率增大幅度2 个重要因素对随机利率风险和母子公司担保所隐含的违约传染风险进行金融意义分析。结果表明:(1)母公司为子公司担保,增强了子公司到期还本付息的能力,提升了子公司的信用等级,从而提高了子公司发行债券的价值,且市场经济越不景气、市场环境震荡越大,母公司为子公司担保所体现的担保价值越大;(2)母公司为子公司担保可能引发违约传染,导致母公司违约概率增大,特别在n家子公司于债券到期日之前肯定违约条件下,母公司条件违约概率增大幅度将是巨大的;(3)母公司应在权衡担保价值和违约概率2 个重要因素下决定担保子公司个数,从而规避违约传染风险造成的损失。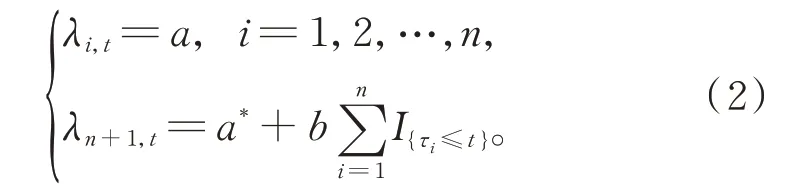
1.2 母子公司担保债券的数学模型和定价公式
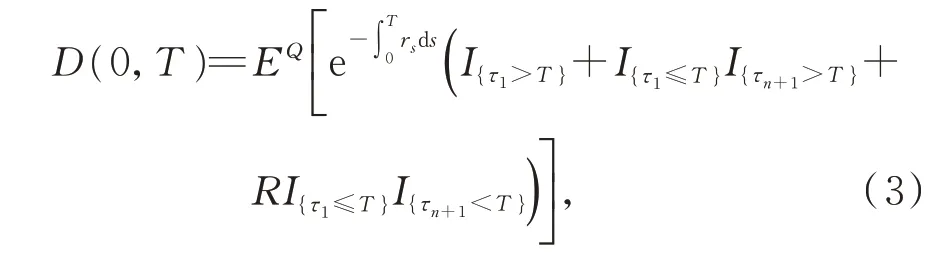
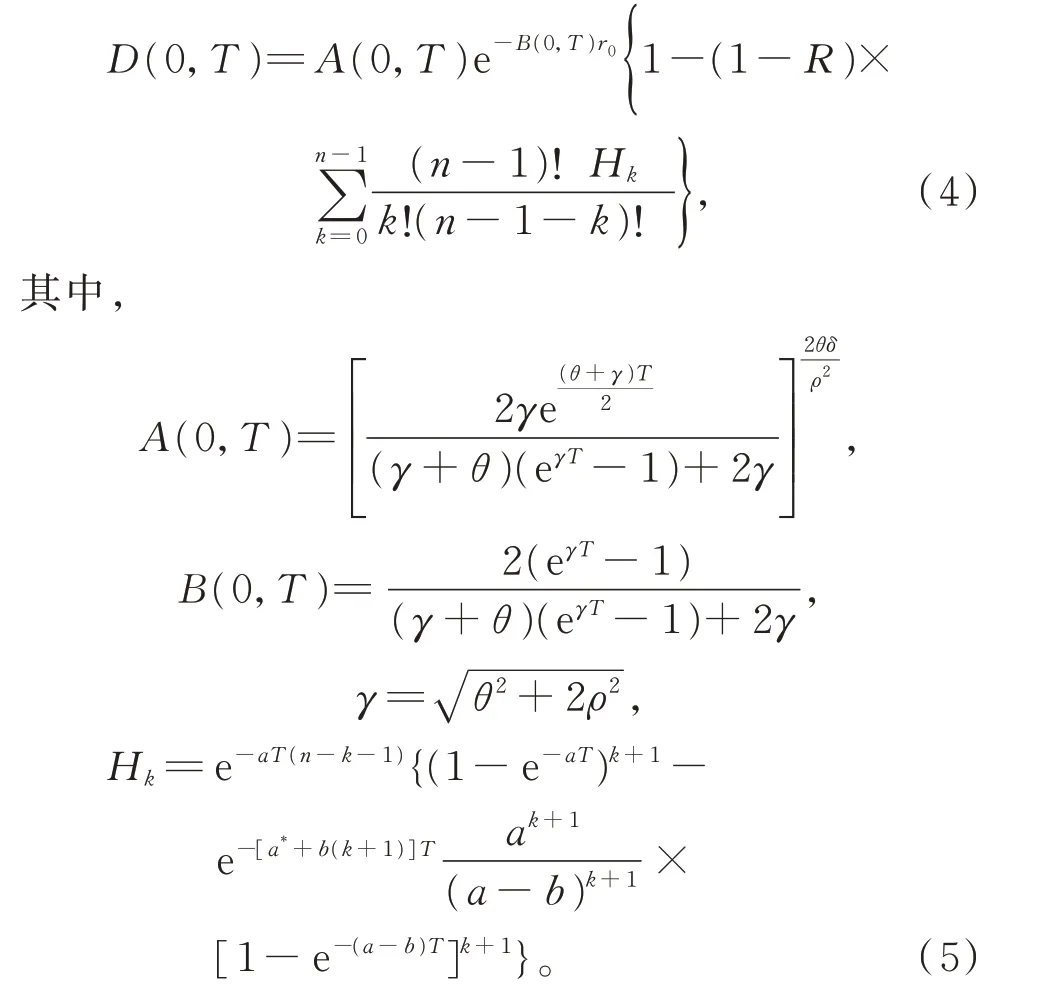
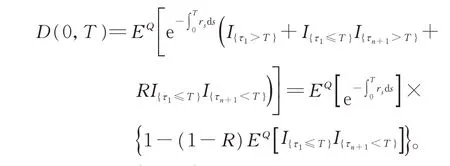
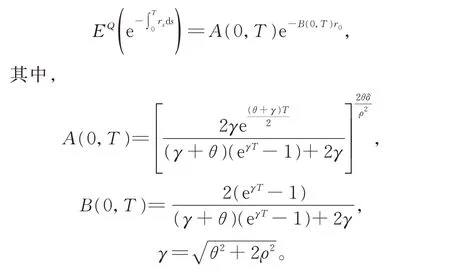
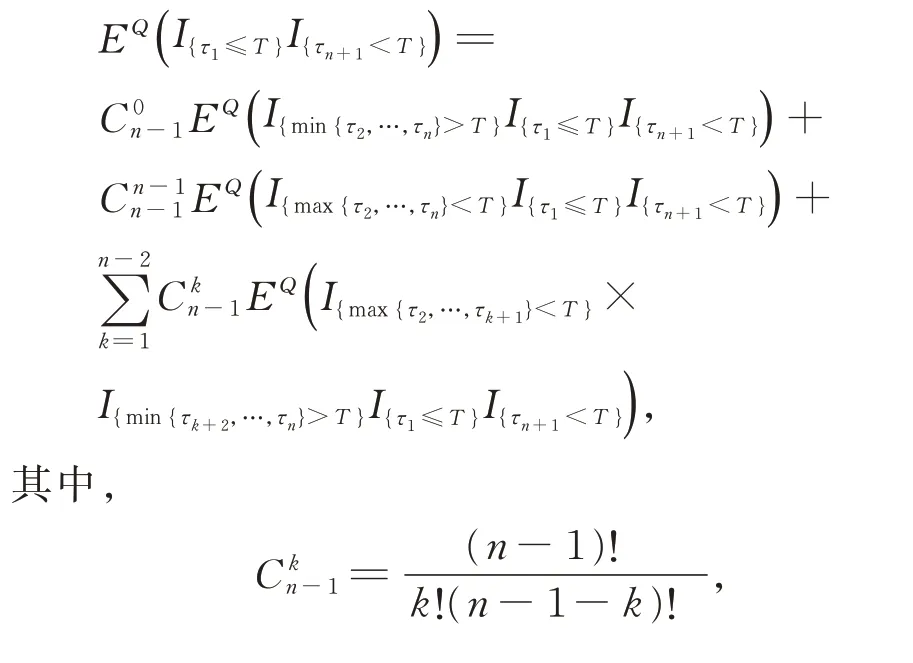
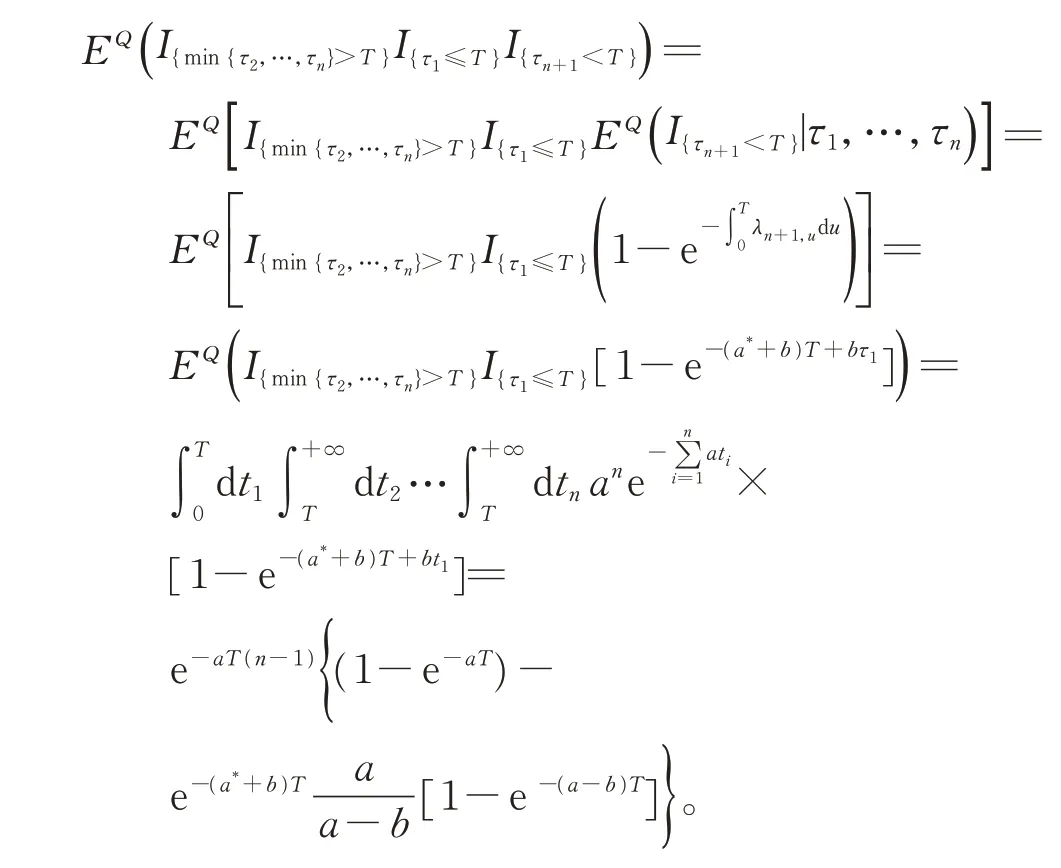

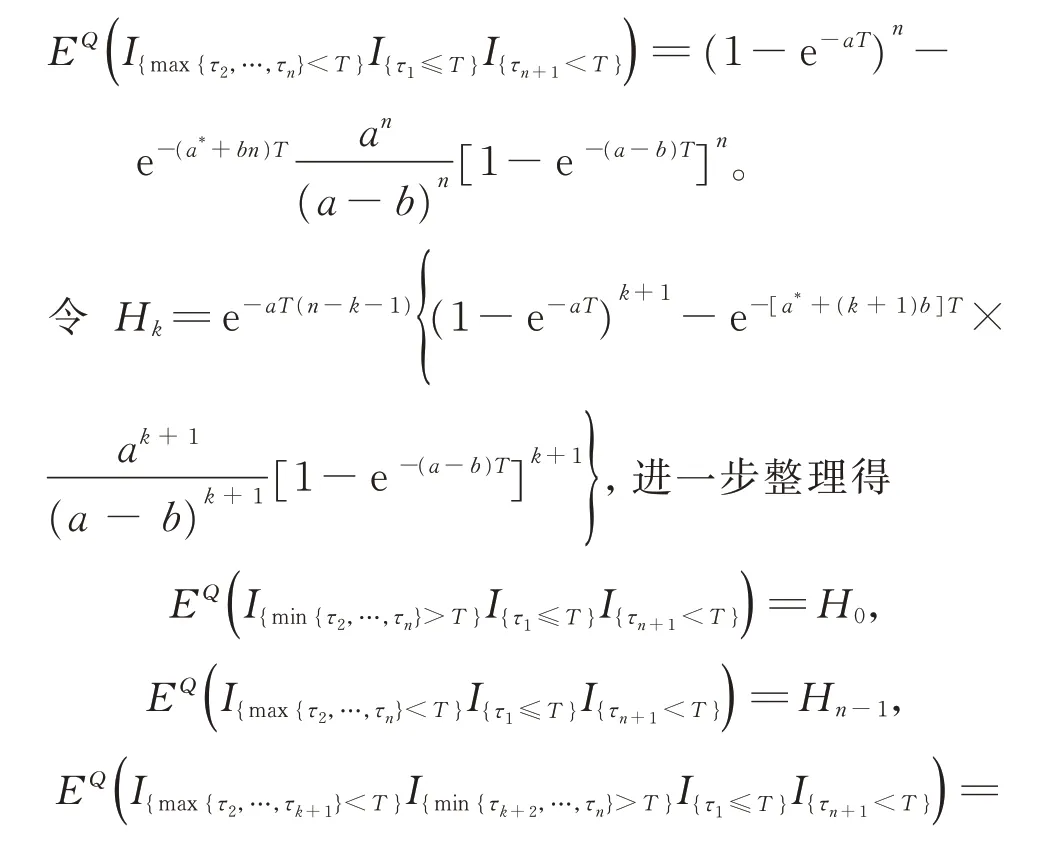
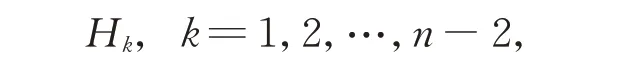
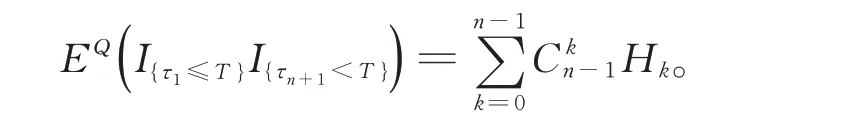
1.3 无担保情形下的公司债券定价
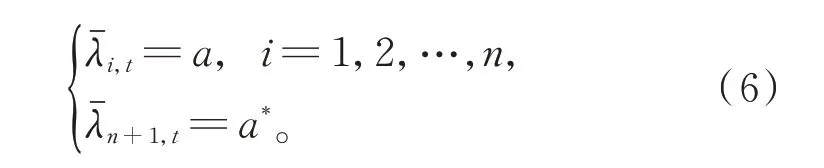
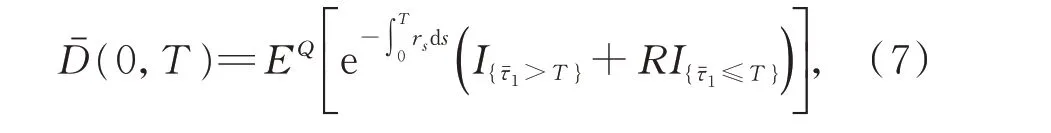
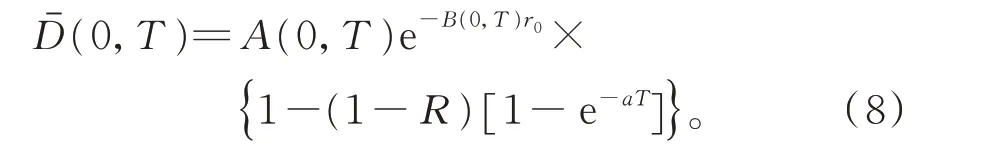
2 金融意义分析
2.1 子公司债券担保价值
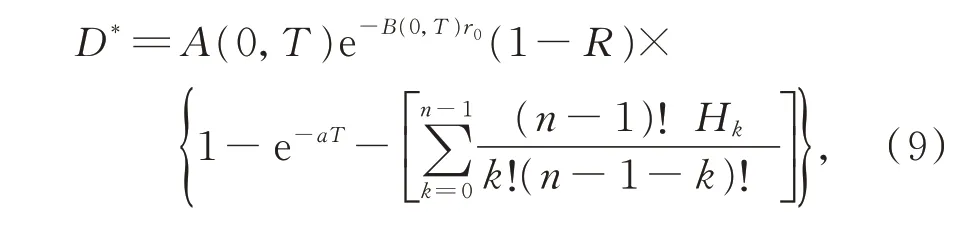
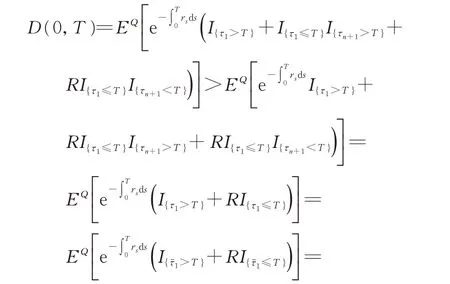
2.2 母公司违约概率
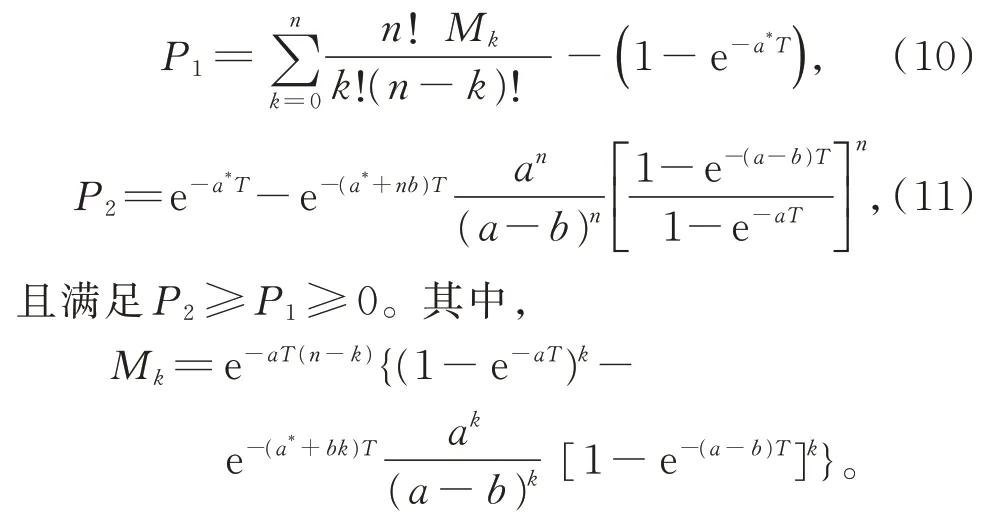
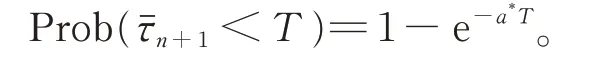

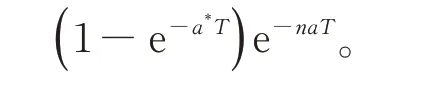
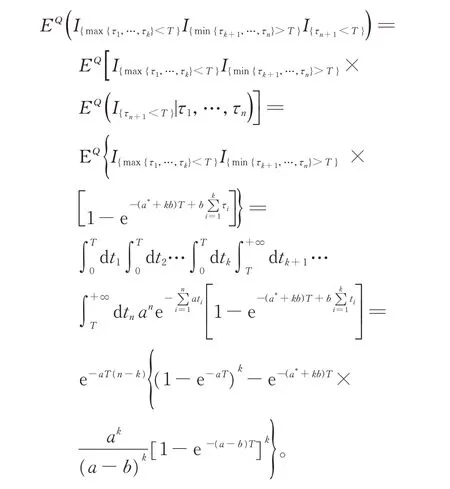

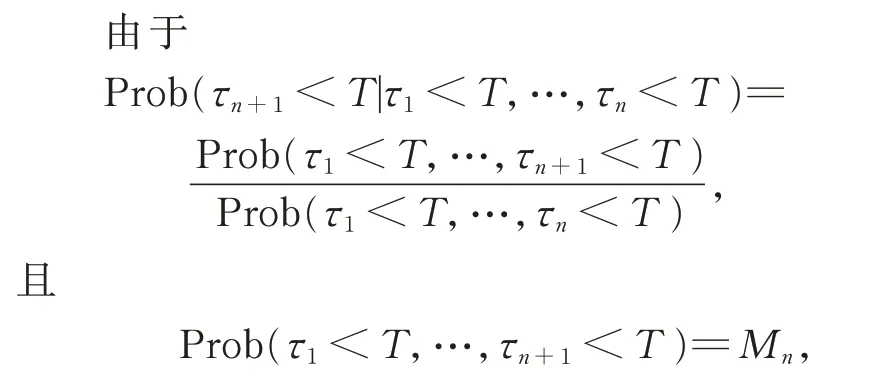
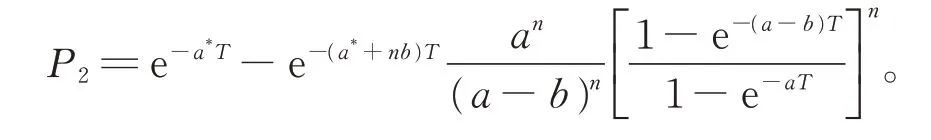
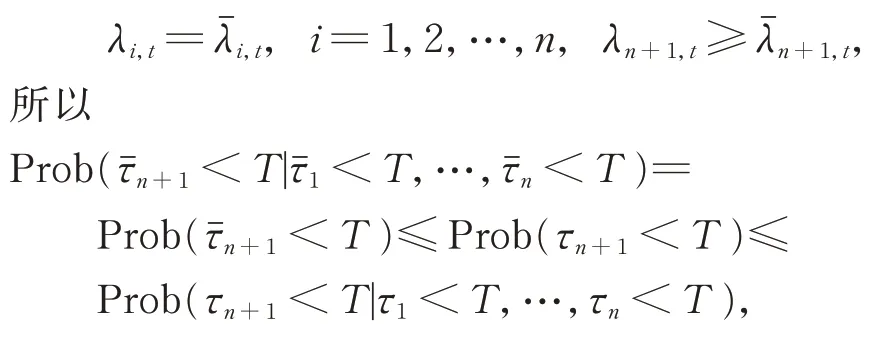
3 数值分析

4 结论

