牛顿-矩阵多分裂多参数TOR 迭代法弱收敛性分析
张理涛,张一帆
(郑州航空工业管理学院数学学院,河南 郑州 450046)
0 引言
考虑光滑非线性方程组[1-2]

其中,F是非线性映像,Ω 是RN中任一有界集,x是Ω的一个向量。对于式(1)的求解,许多学者做了大量研究工作,得到了一系列有效的计算方法[1-8]。但求解非线性方程组的迭代方法大多由求解线性方程组的迭代方法衍生而来。对于线性方程组的求解,LEARY 等[9]提出了基于矩阵多分裂的并行多分裂迭代法。此后开展了许多相关研究并给出了收敛定理,如文献[10-12]研究了系数矩阵的(局部松弛)SOR、AOR 和TOR 方法。文献[13]对SOR、AOR和JOR 松弛方法的收敛速度和发散速度进行了比较。文献[14]分析了不同权矩阵的收敛性。文献[15]研究了系数矩阵的USAOR 迭代法。文献[16]将该方法推广至非线性方程组,构造并研究了牛顿-并行多分裂方法。文献[17]设计并研究了牛顿-全局松弛矩阵多分裂迭代法。本文将求解线性方程组的松弛矩阵多分裂迭代法推广至求解非线性方程组,研究了牛顿-全局松弛非定常多分裂多参数迭代法,建立了局部收敛定理,估计了收敛速度。
求解式(1)的牛顿法为
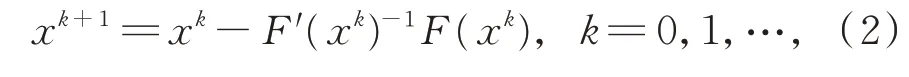
其牛顿方程组为

则式(3)可表示为

式(1)的相关知识可参阅文献[17-18]。若对A(xk)x=b(xk)应用松弛矩阵多分裂迭代法,则可得到牛顿-全局松弛矩阵多分裂迭代法(NGRM 迭代法)。
算法1矩阵多分裂多参数迭代法
任取初始近似x(0)∈RN,对m=0,1,…,重复步骤1和步骤2,直至收敛。
步骤1对t=1,2,…,α,(并行)求解yt:

步骤2计算
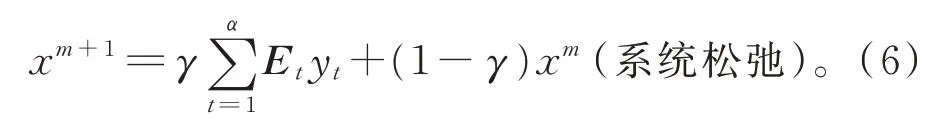
注1yt表示第t台处理机得到的解,Mt表示第t台处理机对应于A(xk)的分裂,Et表示第t台处理机的加权矩阵。
注2如果Et的对角线元素之一为零,则yt不需要计算相应分量,从而大大节省了工作量。这表明Et还扮演着分配每个处理器工作负载的角色。应尽最大努力平衡处理器之间的负载,以降低同步等待的成本。由此可见,算法1 具有天然的并行性。
定义1A=(aij)∈RN×N,ZN×N={A∈RN×N|aij≤0,i≠j}。

(4)若aij≥0,i,j=1,2,…,n,则称A为非负矩阵,并表示为A≥0,记|A|=(|aij|)。
若A−B≥0,则表示为A≥B,可得
引理1若A,B∈RN×N,D=diag(A),
(1)若A为M-矩阵,则D≥0,且D非奇异;
(2)若A为M-矩阵,B∈ZN×N,且A≤B,则B为M-矩阵;
(3)若A为H-矩阵,则A非奇异,且;
(4)已知A,B均为M-矩阵,若A≤B,则A−1≥B−1;
(5)若A为H-矩阵,且A=D−B,则D非奇异,且ρ(|D|−1|B|)<1。
1 牛顿-矩阵非定常多分裂多参数TOR 迭代法
算法2矩阵多分裂多参数TOR迭代法(MTOR)
任取初始近似x(0)∈RN,对m=0,1,…,重复步骤1和步骤2,直至收敛。
步骤1对k=1,2,…,l,(并行)求解yk:

步骤2计算

算法2 可改写为
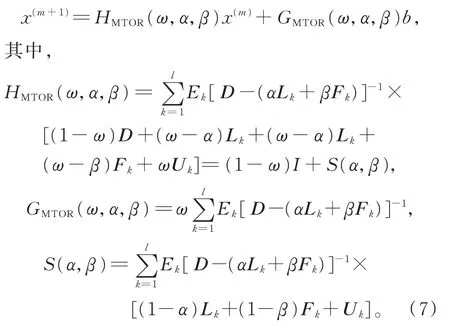
引理2若A∈Rn×n是H-矩 阵,令A=D−B=D−Lk−Fk−Uk(1≤k≤l),其 中D=diag(A),Lk,Fk是严 格意义下的三角矩 阵,而Uk是一般矩阵,且(D−Lk−Fk,Uk,Ek),k=1,2,…,l,是矩阵A的多分裂TOR 法且满足。如果

引理3[20]若A∈Rn×n是H-矩阵,令A=D−B=D−Lk−Fk−Uk(1≤k≤l),其 中D=diag(A),Lk,Fk是严格意义下的三角矩阵,而Uk是一般矩阵,且(D−Lk−Fk,Uk,Ek),k=1,2,…,l,是矩阵A的多分裂TOR 迭代法且满足。如果

则ρ(HMTOR(ω,α,β))≤ρ(|HMTOR(ω,α,β)|)<1。

则ρ(HMTOR(ω,α,β))≤ρ(|HMTOR(ω,α,β)|)<1。

3 收敛性分析
为证明引理2,需证明9 种可能的情况(表1)。

表1 参数α,β 的不同区域Table 1 Different areas of the parameter α,β
引理2的证明由于ρ(S(α,β))≤ρ(|S(α,β)|),只需证明ρ(|S(α,β)|)<1。定义

由假设条件易知,D−αLk−βFk是H-矩阵,k=1,2,…,l。由引理5 及比较矩阵定义,知
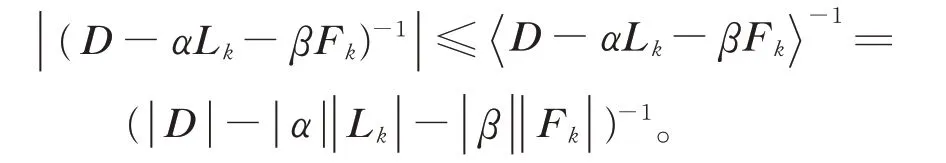
因此,可得


考虑矩阵A′k,k=1,2,…,l的分裂:

令γmin=min {α,β},有

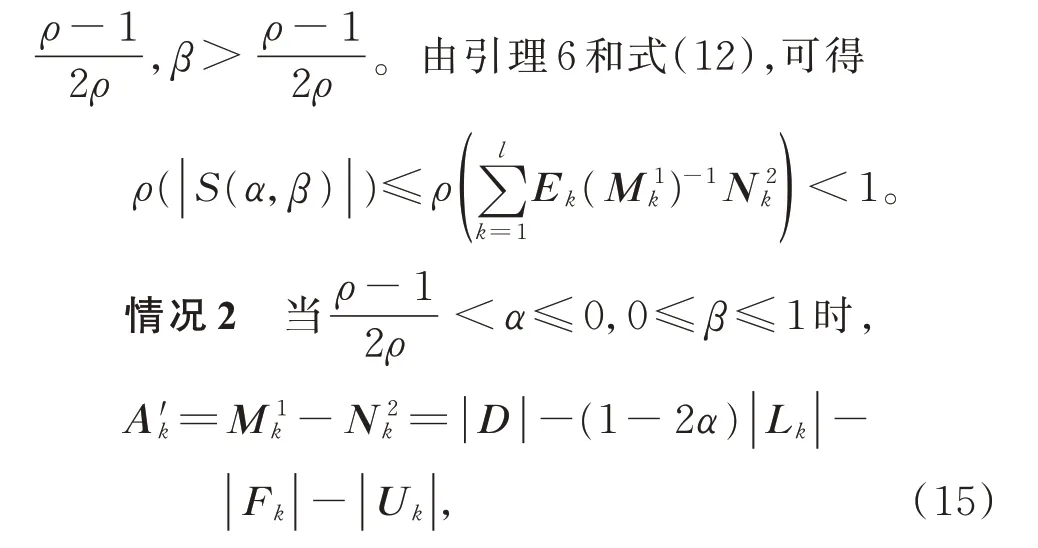
由于α≤0,0 ≤β≤1和−1≥−(1−2α),可得

(i)当 1−2α≥2β−1 时,有−(1−2α)≥−(2β−1),由于α≤0 和−(1−2α)≤−1,可得

(ii)当1−2α≥2β−1 时,有−(2β−1)≤−(1−2α),由于β≥1 和−(2β−1)≤−1,可得

由于β≤0和−1≥−(1−2β),可得

由于A是H-矩 阵,是单调矩阵,k=1,2,…,l且ρ<1。由引理6 和式(12),可得

由于β≥1和−1≥−(2β−1),可得

(i)当2α−1≥1−2β时,有−(2α−1)≤−(1−2β),由于α≥1 和−(2α−1)≤−1,可得

(ii)当2α−1≤1−2β时,有−(1−2α)≤−(2β−1),由于β≤0 和−(1−2β)≤−1,可得
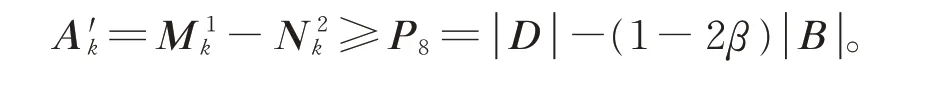

由于α≥1和−1≥−(2α−1),可得
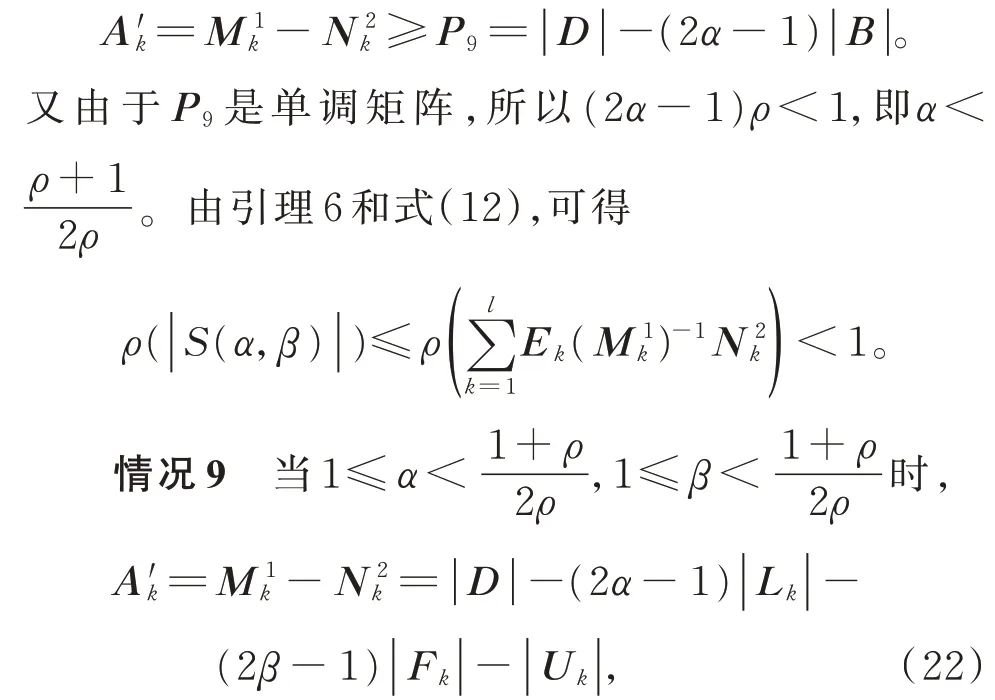
令γmax=max {α,β},则

4 结论
当牛顿方程的维数较高时,牛顿法的计算量将非常大,其精确解的计算成本较高。在已有研究基础上,通过引入多重松弛因子,提出了牛顿-矩阵多分裂多参数TOR 迭代法,建立了局部收敛定理,并估计了收敛速度。

