朗伯三锥体的后向LRCS
宫彦军,谭佳伟
(湖南科技学院 智能制造学院,湖南 永州 425199)
随着国家对国防科技的发展越来越重视,对国家安全,特别是对国家领空安全的重视,使得目标雷达散射截面(LRCS)测量系统对雷达散射截面的研究有了更加实际的指导意义。Wang等[1]对LRCS模型验证在基于特征的选择验证方法的基础上进行实验研究,可以运用在民用方面和在军事方面上,就导弹方面而言,基于LRCS系统的自动跟踪技术是很重要的[2]。在远、小、快等特性的目标上,郝晓慧等[3]分析在最小距离限的LRCS研究。罗龙[4]的外场测量的补偿计算,则有着很深的借鉴意义。把目标“点”化,是物理上的常用手段,如果点化就能使得目标的测量其LRCS的计算易于系统研究[5],非理想条件下的测量对精度有很高的要求[6]。LRCS能够全面又客观地体现出各种因素对目标激光散射特性的影响,其中包括激光的波长、目标的材料特性及几何形状[7-8]、目标所处大气环境等[9]。孙绎成等[10]所研究的隐身飞行器LRCS特性对我国国防与民用航空激光雷达等方面也有一定的促进作用。李双江[11]在散射体远红外波段上进行研究。利用激光散射特性来发现、识别目标[12]。经过对LRCS测量的进一步研究分析,包学志等[13]研究精度的影响范围进一步扩大,其还应包括背景散射。在理想条件下要求获得散射光的功率,可运用激光测量系统来计算。非理想条件下,包学志等[14]所研究的校正方法使得LRCS测量结果更接近事实,运用更广。王明军等[15]在复杂目标的LRCS的数值计算,研究不仅限于可见光。李良超等[16]对在目标实物上覆盖多种材料,一一控制变量因素,进行LRCS计算,使得飞机的战略隐形技术得到理论支持。张骏等[17]的弹道导弹弹头的LRCS相干分量预估也是很关键的。开展目标光散射的研究是很有必要的,这些方法将可能会影响到整个系统性能的目标实物的散射特性[18-19]。Cao等[20]给出凸回转体的LRCS的计算方法,采用的是统一积分法,缺点:一是存在舍掉误差,二是不适用于非凸的回转体。本文设计朗伯三椎体的后向LRCS的计算算法,给出统一积分法和差异积分法的两种计算方法,其中差异积分法能克服统一积分法中存在的舍掉误差,这个误差是在计算时分母为0时舍掉的误差。利用射线跟踪设计遮挡剔除算法,实现朗伯三椎体后向LRCS的精确计算。
1 三锥体的LRCS算法
1.1 目标面元的LRCS
三锥体目标上每一可照射面元后向LRCS为:
dσ=4πfr(β)cos2βdA,
(1)
其中:fr(β)为三锥体表面材料在后向方向上的双向反射分布函数,是面元的本地入射角β的函数,当表面材料为朗伯面时,fr(β)是一个常数,fr(β)=ρ/π,ρ是表面材料的半球反射率,对于理想朗伯体fr(β)=1/π;dA为面元面积的微分。对于凸目标上满足cosβ>0的点就可以被照射到。将fr(β)=1/π代入式,同时考虑到cosβ>0可照射,凸目标上表面面元的后向LRCS为:
dσ=(cosβ+|cosβ|)2dA。
(2)
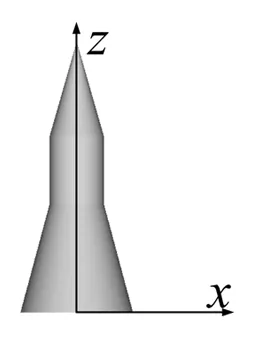
图1 三锥体坐标系框架
三锥体表面的所有面元后向LRCS的累加就是三锥体的后向LRCS。cosβ是面元法线与观测方向的夹角的余弦,可以用法线方向的单位矢量与观测方向的单位矢量的内积计算。三锥体形状和坐标系如图1所示。其中,圆台高h0,圆台半锥角α,圆柱高h1,圆柱半径r,圆锥高h2。令h=h0+h1+h2为三椎体的高。坐标系的原点为底面圆心,三锥体的轴为z轴,选与z轴垂直的一个方向建立右手直角坐标系,圆心为点O,三椎体侧面的方程由式给出,底面在xOy平面半径为r+h0tanα。
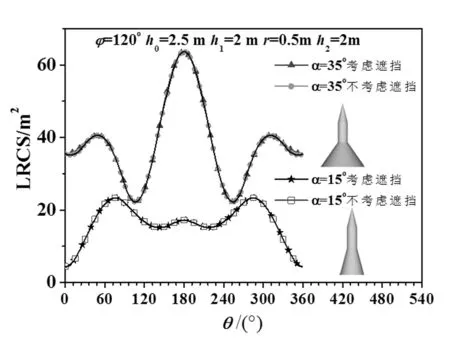
x2+y2-f02(z)=0(0≤z≤h0),x2+y2-r2=0(h0 x2+y2-f12(z)=0(h0+h1 (3) (4) 观测方向的天顶角为θ、方位角为φ,观测方向的单位矢量S为: S=(sinθcosφ,sinθsinφ,cosθ), (5) 球坐标系的天顶角θ为0°~180°,本文为0°~360°,对给定的φ,当θ大于180°时,这时天顶角为360°-θ,当φ≤180°时,方位角为180°+φ,则此时的方向矢量为: S′=(sin(360°-θ)cos(180°+φ),sin(360°-θ)sin(180°+φ),cos(360°-θ)), (6) S′=(sinθcosφ,sinθsinφ,cosθ) 。 (7) 从式(7)可以看出,对于θ>180°,φ≤180°,可以认为此时的天顶角为θ,方位角还是φ,用球坐标计算的方向矢量也是正确的。对于θ>180°,φ>180°,这时天顶角为360°-θ,方位角φ-180°,可以认为是180°+φ,对于θ>180°,φ>180°,把θ、φ作为天顶角、方位角计算出来的方向一致。因此对于给定的方位角φ,θ可以为0°~360°。S的x、y、z分量分别为Sx、Sy、Sz。则Sx=sinθcosφ,Sy= sinθsinφ,Sz=cosθ。 根据式(2)得 (8) 三锥体表面任意一点的法线方向单位矢量为n,式(8)中cosβ为: cosβ=n·S。 (9) 根据式(9)、(5)和(3)得式(10) (10) 因为三椎体不是凸体,锥柱和圆台之间存在遮挡。利用射线跟踪设计剔除遮挡的原理是,从目标上面元的中心点沿着观测方向发出一条射线,如果与目标相交,这个面元被遮挡,否则没有遮挡。 1.3.1 遮挡 从目标表面上的点(x,y,z)沿着观测方向发出的射线上的点p为: p=(x,y,z)+lS, (11) 对于三椎体的锥柱和圆台之间的遮挡,把式(11)代入式(3)得关于l的一元二次方程: al2+bl+c=0 。 (12) 圆台、圆柱、圆锥遮挡的a、b、c分别由式(13)、(14)和(15)给出, a1=Sx2+Sy2-Sz2tan2α,b1=2[xSx+ySy+(r+h0tanα-ztanα)Sztanα],c1=x2+y2-(r+h0tanα-ztanα)2, (13) a2=Sx2+Sy2,b2=2(xSx+ySy),c2=x2+y2-r2, (14) (15) 根据式(12),可得: (16) 根据式(16),存在下面的结论: 1)如果a≠0 (1)如果b2-4ac<0,l无解,面元没有被遮挡; 2)如果a=0,根据式(12)得: bl+c=0 。 (17) (1)如果b≠0,l=-c/b。如果l>0,并且z1≤z+lSz≤z2,遮挡;否则不遮挡。 (2)如果b=0,不遮挡。 其中,z1、z2分别为目标z值的最小值、最大值。 1.3.2 遮挡函数 根据上面的讨论,引入遮挡函数Vis(x,y,z,θ,φ,a,b,c)为: (18) 1.3.3 统一积分法 根据式(8)朗伯三椎体统一积分法的后向LRCS计算公式为: (19) 1.3.4 差异积分法 (20) 式(19)和(20)对比,对于侧面的计算,式(19)采用dxdz积分,而式(20)用dxdz和dydz两种积分方式,所以称为差异积分法。 当θ=0°时可以推导出三椎体的后向LRCS的理论值为: (21) 图2 不同h0三椎体的统一积分法计算的后向LRCS随着φ的变化 θ=0°,h0=2.5 m,α=15°,h1=2 m,r=0.5 m,h2=2 m。理论值:4.400 1 m2。本文的计算结果与计算精度有关,Δz=Δx=Δy为2 mm、1 mm、0.5 mm、0.1 mm的计算结果分别为4.393 35 m2、4.396 8 m2、4.398 4 m2、4.399 8 m2。本文的计算精度:Δz=0.5 mm、Δx=0.5 mm、Δy=0.5 mm。 θ=120°,α=15°,h1=2 m,r=0.5 m,h2=2 m,h0由2.5 m变化到0 m,变化间隔为0.5 m三锥体的统一积分法计算的激光后向LRCS如图2所示。 图3 不同h0三椎体的差异积分法计算的后向LRCS随着φ的变化 由图2可知,θ、α、h1、h2、r取固定值时,能够看出h0越小,三椎体的后向LRCS也随之变小。不同h0的RLCS计算的结果不同,当h0等于2.5 m时最大,即三锥体的圆台高越大,计算结果越大。这是因为目标的尺寸变大。三椎体的轴为Z轴,当θ固定时,φ变化,由于轴对称,后向LRCS应该不变,根据式(19),计算时分母会出现为0的情况,舍掉,存在舍掉误差,所以图2给出的结果存在波动。 θ=120°,α=15°,h1=2 m,r=0.5 m,h2=2 m,h0由2.5 m变化到0 m,变化间隔为0.5 m三锥体的考虑遮挡的差异积分法计算的激光后向LRCS随着φ变化的结果如图3所示。 由图3可知:θ,α,h1,h2,r取固定的值时,差异积分法计算的后向LRCS随着方位角的变化,变化很小,LRCS变化不大,这是因为采用差异积分法分母不会出现为0的情况,不存在舍掉误差。 φ=120°、h0=2.5 m、h1=2 m、r=0.5 m、h2=2 m,α=15°、35°差异积分法考虑遮挡和不考虑遮挡计算的激光后向LRCS随着θ的变化如0图3所示。 从图4可知:α=15°,在θ=75°、180°、285°附近存在3个峰值。对于圆台,θ=90°-α=75°,在此方向上圆台有法线为观测方向的面元,本地入射角为0°,对于圆锥,圆锥的半锥角=artan(0.5/2)=14.0°,峰值为θ=76°位置,因此在75°到76°为峰值位置;180°是底面的贡献,这时底面的法线为观测方向;285°为对称位置。α=35°,圆台θ=55°为峰值位置,圆锥在76°位置,图中的峰值位置为49°,180°、311°存在峰值。两条曲线以180°为中心存在中心对称,这符合三椎体的对称性。从图4中看不出考虑遮挡和不考虑遮挡的区别,不考虑遮挡与考虑遮挡的差值如图5所示。 图4 差异积分法考虑遮挡和不考虑遮挡计算的激光后向LRCS随着θ的变化 图5 差异积分法考虑遮挡和不考虑遮挡计算的激光后向LRCS的差值随着θ的变化 从图5可以看出,考虑遮挡和不考虑遮挡,两者的LRCS存在差值,有的位置不存在遮挡,对于θ=0°、90°、270°理论上不存在遮挡,图5给出的结果也给出同样的结论,两者的差值为0。 设计朗伯三锥体的后向LRCS的计算算法,从理论上进行朗伯三锥体LRCS公式的推导。设计两种计算方法:统一积分法、差异积分法。利用射线跟踪设计剔除遮挡算法,提高计算精度。分析观测方向的方位角、天顶角对LRCS的影响,分析三椎体的几何参数对后向LRCS的影响,能清楚地得出不同影响因素对LRCS的影响。对于目标的不同尺寸,计算所得的LRCS值也不同。从给出的测试结果可以看出,朗伯三锥体的LRCS算法可以给出正确的结果,设计的剔除算法提高了计算精度。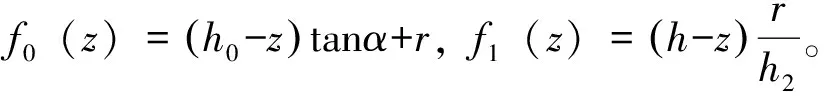
1.2 LRCS公式
1.3 射线跟踪剔除遮挡
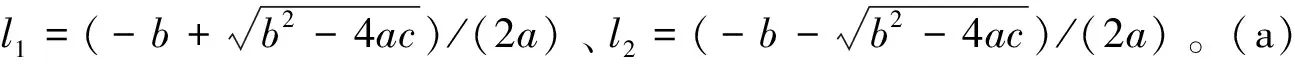
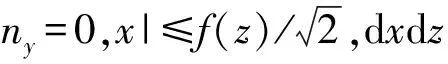
2 三锥体LRCS计算与讨论
2.1 理论值与数值对比
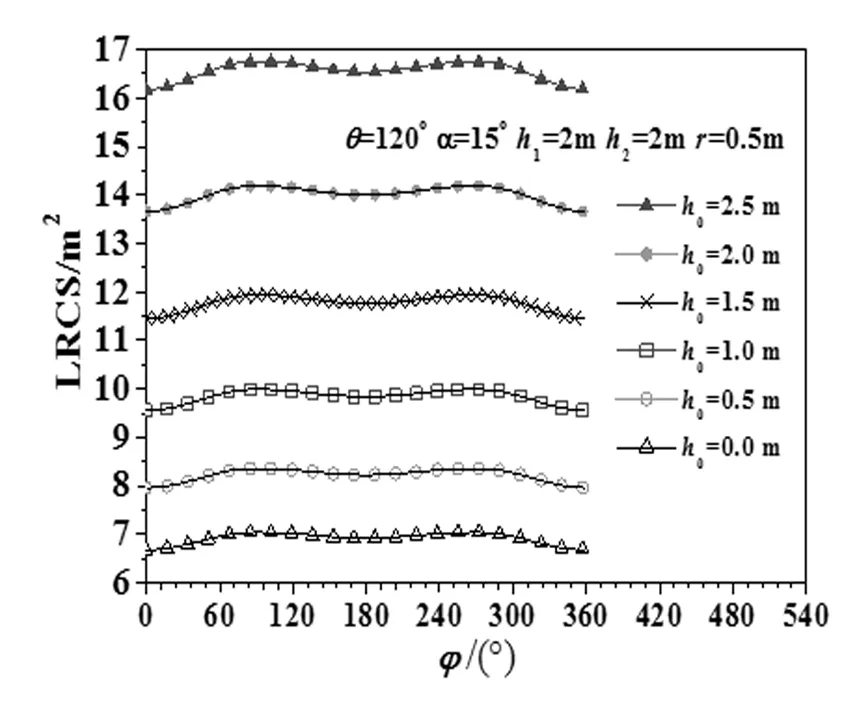
2.2考虑遮挡的统一积分法
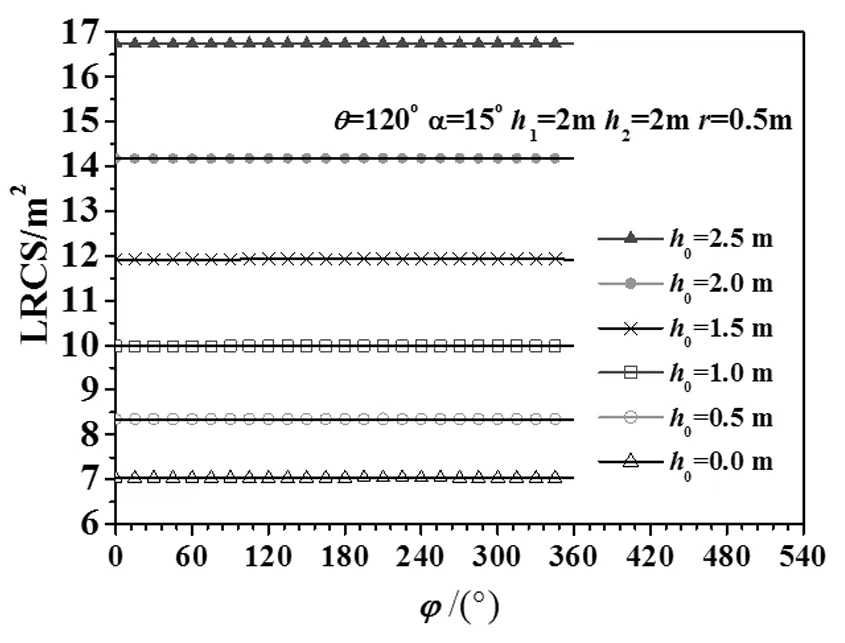
2.3 考虑遮挡的差异积分法
2.4 差异积分法考虑遮挡和不考虑遮挡
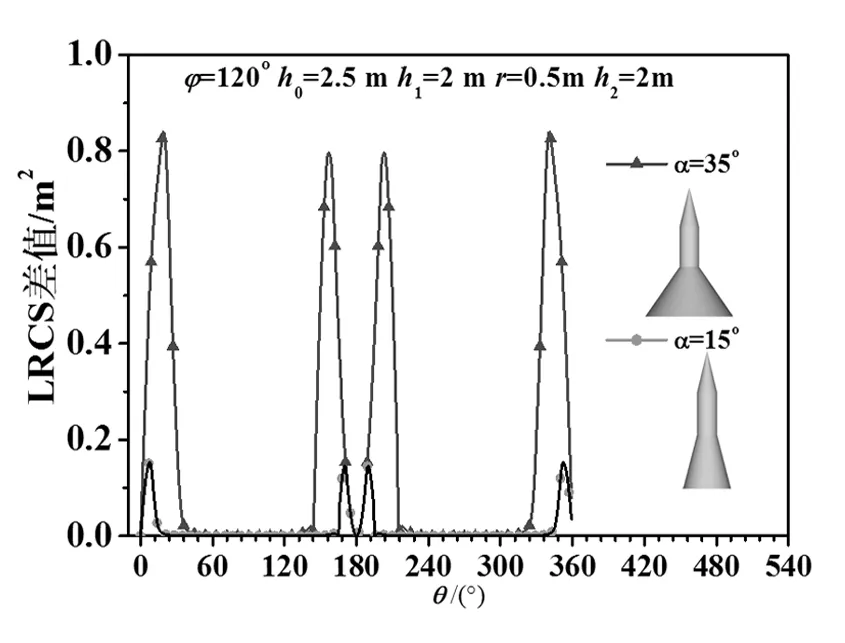
3 结语

