基于数学模型下平板折叠桌的创意设计

覃雪清，翁世有

(1. 桂林信息科技学院 数学教研部， 广西 桂林 541004；2. 苏州市职业大学 基础部，江苏 苏州 2151041)

折叠桌因其占地面积小，易折叠的优点，受到诸多企业的欢迎。在众多的公共场合如酒店等经常会看到折叠桌和折叠椅，但其牢固性和灵活性受其设计参数的制约，因此恰当的参数设计有助于提高其商用价值。

图1 平板折叠桌示意图

由图1可知，桌面呈圆形，多根木条组成桌腿且木条有空槽可滑动，桌腿可随铰链的活动平铺成一张平板。桌子外形由直纹曲面构成，造型美观。不管在做任何商品时，商家都会考虑三大重要顾虑：一是耗材多少问题，能否尽最大可能节省材料，减少不必要的浪费以期减少制作经费，使利益最大化；二是工艺品是否美观问题，商品是用来出售的东西，对于违反人类审美观的商品是走不远的；三是实际工艺操作中能否实现该折叠桌的制作。

就以上的三个顾虑的考量，文章利用数学模型拟解决以下三个实际问题：

(1)已知长方形平板120 cm(长)×50 cm(宽)×3 cm(厚度)，木条宽为2.5 cm，折叠后桌子的高度为53 cm。对于给定的数据设计出此折叠桌的的各个参数如桌腿木条开槽的长度和桌脚边缘线等。

(2)给定折叠桌高度和桌面直径，讨论矩形平板材料和折叠桌的最优设计加工参数。

(3)根据问题1和问题2所建立的模型设计几个设计的创意平板折叠桌。要求给出相应的设计加工参数。

表1 符号及文字说明

续表1

其他符号使用时会在文中说明。

2 问题1的求解

文章的模型是假设实际加工误差对设计无影响、钢筋尺寸不计以及切割木条损耗很小不计木条间空隙的基础之上建立起来的。

2.1 求解木条长度

如图2所示，由对称性，只取1/4平板、8根木条进行研究，图中从下至上木条的编号为1，2，...，8。取第一根木条中点B，连接OB,设AB=d1，在直角三角形OAB中应用勾股定理计算：

(1)

可求解出第一根木条的长度L1。同理可求其余木条的长度：

(2)

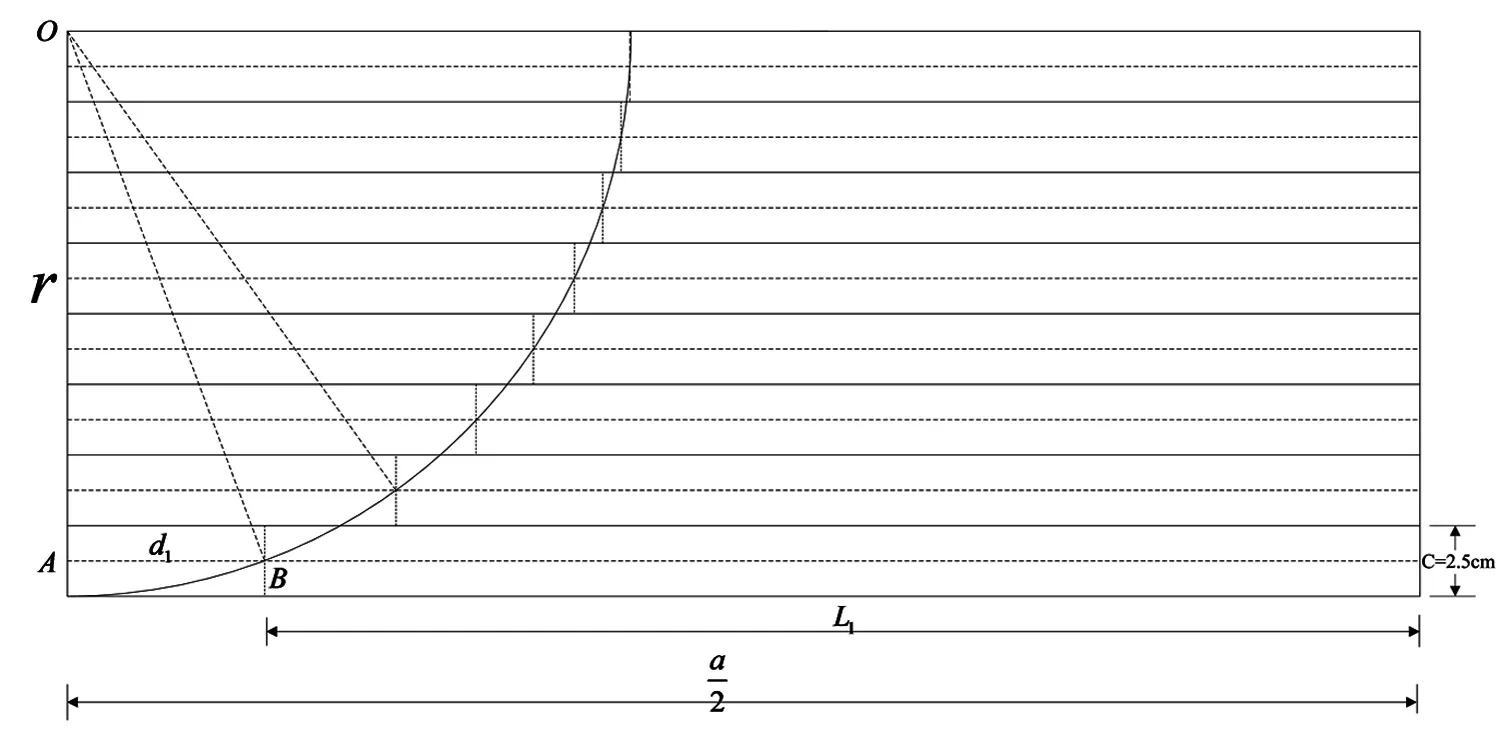
图2 木条编号示意图

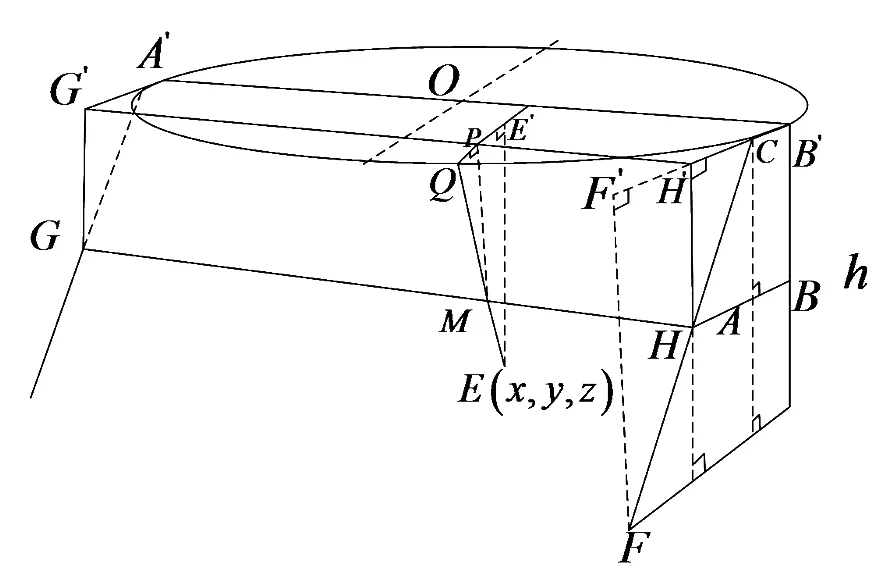
图3 折叠桌几何示意图

利用MATLAB编程[1]求解得出各木条长度如表2所示。

表2 各木条长度

2.2 求解开槽长度

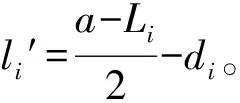
取圆周上任意点Q，M点为折叠后钢筋与木条的交点.作MP⊥G′H′,由射影定理，P位于线段G′H′上，在RtΔPQM中，

PQ=di-HB，

HB=HA+AB，

联立方程，解出开槽下端点到木条上端点的距离li″。利用MATLAB编程[3]，得表3数据。

表3 木条开槽长度

2.3 确定桌脚边缘线上点的坐标

取每根木条底端的中点，求出坐标。为了确定各点坐标，以桌面圆的圆心作为坐标轴起点，沿半径方向作x轴，y轴，垂直向上作z轴建立直角坐标系，具体如图4所示。 取桌脚边缘上任意一点E(xi,yi,zi)。

图4 直角坐标系下的折叠桌示意图

(2)求E点在z轴方向上投影.显然转化为求EE′长度。RtΔPQM～RtΔE′QE。由相似三角形的性质，有：

根据以上算法，用MATLAB编程[1]求出EE′长度.则z轴方向上投影：z=-|EE′|。

(3)求y轴方向上投影。由于平板桌折叠过程中木条平行移动，而木条折叠后，部分木条向内凹，部分木条向外凸，故分两种情况讨论。

情形一: 木条折叠后向内凹。求yi即转为求E′N长度。由图4中的几何关系可得：

此时yi=-|NE′|。

情形二：木条向外凸。如图5，取圆周上一点R。KK′垂直于J′R，JJ′垂直于J′R。由图中的几何关系，建立关系式：

此时yi=-|J′I|。

用Matlab编程[4]求出桌脚边缘线上点的坐标并画出对应曲线图5。

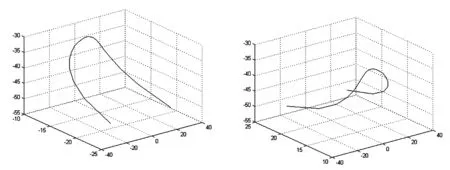
图5 桌脚左边与右边的边缘线

3 问题2模型的建立与求解

问题2属于一定约束条件下的优化问题.假设平板的厚度为3 cm，每根木条的宽度为4 cm。对产品的稳固性、加工难易程度、材料使用情况综合考虑。

产品的稳固性从两方面考虑。其一，考虑最外侧的四条桌腿的接地点形成的四边形，分析证明出当该四边形为正方形时，折叠桌的稳定性最强，同时材料也得到充分合理的利用；其二，我们考虑将位于最外侧的木条平移，平移后与最中间的的木条相交，如图4所示。理想情况下，三角形AOB为等边三角形时，由力的合成知此时可承受的合力最大，折叠桌稳定性最好[5]。

产品的加工难易程度与开槽的长度有关。因此，我们用所有木条槽长之和刻画加工的难易程度，即槽长之和越小，加工难度越小。钢筋位置应该与木条的槽长有一定关联，考虑用射影几何[6]相关知识求解。

3.1 讨论稳定性与材料最大化利用

圆桌面在水平地面的投影和4条桌脚的着地点的位置关系如图6a、6b和6c所示，将这三种情况进行受力分析[7]得出结论：(1)对比图6a，图6b时发现，当图6c中左右两条边越往圆周靠近，桌脚越短。所以，出现图6a时较省材料；(2)对比图6a，图6c时发现，当出现图6c时，由物理理学分析可知，当AB的长度小于桌面直径时，桌子支撑力将随着AB的减小而减小，所以，当出现图6a情形时，较为稳定。综合考虑，图6b对材料造成浪费，图6c稳定性不高，而图6a中，ABCD为正方形且与圆相切，这样可以保证稳定性的同时也不造成材料浪费。故本文的分析以图6的情形为基础。

3.2 讨论稳定性与钢筋穿过的位置

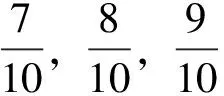
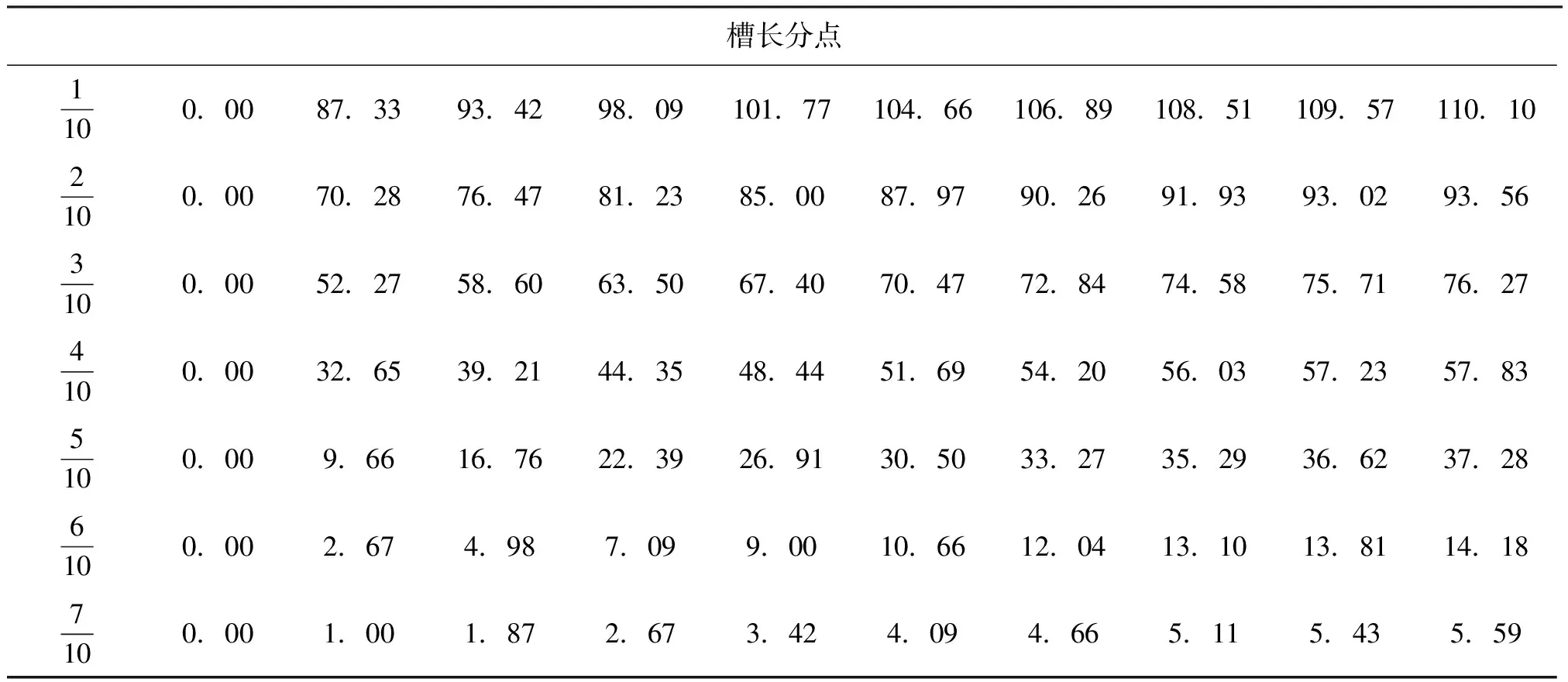
表5 各等分点开槽长度

表6 各等分点总槽长

如图7所示，将最外侧木条CF平移至与中间最短木条相交，连接点A,B,G得ΔABG。当ΔABG为等边三角形时，折叠桌能承受的合力最大[8]。假设木条厚度为3 cm，木条宽度为4 cm，从实际考虑，对位于中间的木条，其开槽的上端至圆边界保留3 cm比较合理。

图7 折叠桌最大受力状态图

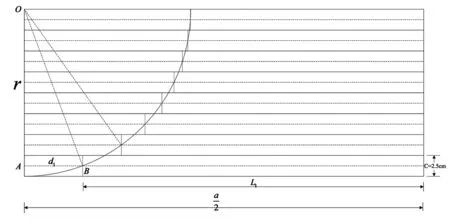
图8 木条长度关系示意图

因此，设置求解开槽长度的算法，步骤如下:

(1)开槽点与圆面交点的距离为：KF=r-d1+3，

现对题目中桌高70 cm，桌面直径80 cm的情形进行讨论，根据MATLAB编程[9]，最终求得开槽长度如表7。

表7 各木条开槽长度 cm

3.3 确定各木条长度及平板尺寸

如图10，在直角三角形CEF中，利用勾股定理确定最外侧木条的长度L1:

(70-3)2+(r-di)2=L12，

同理可求其余木条的长度：

根据程序计算，求得二分之一圆周上的各木条长度如表8所示。

表8 各木条长度

平板宽度及厚度已经确定，只需考虑平板长度。平板长度为：a=2Li+2di。

4 问题3的求解

针对问题3，在问题2的基础上，提出折叠桌的制作过程中应当考虑的优化条件及考虑的最优参数情况，给出一款“8”字形的桌子的设计方案如图9、图10所示。

假设所用材料切割的木条的宽度均为2.5 cm，木板的厚度均为3 cm。图形桌面的设计步骤如下：

步骤1 考虑到产品的稳固性、加工方便和用材少，我们可以根据第二题的讨论来确定参数，即要让桌面的底角所连成的多边形恰好是桌面在地表面的投影的外切图形，则据此我们可以算出木条的长度Li=(r-di)2+(h-c)2。

步骤2 考虑到尽可能地让最短的腿与最长腿投影过去刚好能围成正三角形时最稳定，因此，开槽点就应选取在距离最长木条端的长度为r-di+3 cm处；

步骤3 最后利用勾股定理计算出每根木条开槽的长度(具体的计算参数结果，可由Matlab编程得到)。

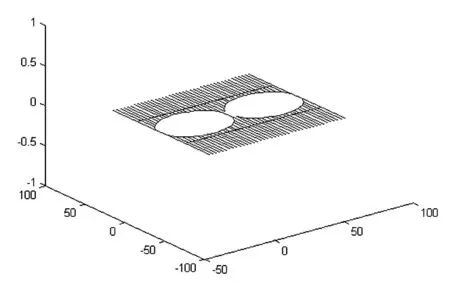
图9 折叠后状态图

图10 折叠前状态

5 结语

针对问题1，对于已知的长方形平板尺寸，通过建立空间直角坐标系，刻画折叠桌面上的点的坐标。从点的运动轨迹，分析坐标从起点到终点的变化。由所求坐标，计算出折叠桌的四分之一圆周的10根木条开槽的长度为：

表9 问题一各木条开槽长度

针对问题2，关于折叠桌的最优设计加工参数，属于多目标规划问题[9]。对于问题2中给定的桌高和桌面直径代入所建立的模型，求解出最优的设计参数，其中开槽长度求解公式为[10]：

开槽长度的值如表10所示。

表10 问题二各木条开槽长度 cm

针对问题3，在问题2的基础上，提出折叠桌的制作过程中应当考虑的优化条件，并给出了几款形状的折叠桌的设计算法。并根据所考虑的最优参数情况，给出一款“8”字形的桌子的设计方案，并画出其位置变化图。