高频RCS预估中判别阴影区域的并行算法

张月园，刘志伟，张晓燕，刘颖婷，何 姗

高频RCS预估中判别阴影区域的并行算法

*张月园1，刘志伟2,3，张晓燕2,3，刘颖婷2，何 姗2

(1. 华东交通大学国际学院，江西，南昌 330013；2. 华东交通大学信息工程学院，江西，南昌 330013；3. 毫米波国家重点实验室，江苏，南京 210096）

利用物理光学方法预估高频雷达散射截面(RCS)时，需要判别目标表面的阴影区域。本文提出了一种基于树型结构的多重阴影判别算法，将判断面元是否被面元遮挡转变为判断面元是否被分组遮挡，极大地降低了计算复杂度。与此同时，引入并行技术，将基于树型结构的多重阴影遮挡算法并行化，进一步节省计算时间。数值算例表明，基于树型结构的多重阴影判别算法与传统的阴影判别方法相比，在保证计算精度一致的前提下，计算效率更加高效。

电磁场；高频散射；并行遮挡判别；计算电磁学；物理光学

高频电磁散射是指电尺寸较大目标的电磁散射。作为雷达目标特性研究的重要手段，采用电磁散射理论高效分析高频电磁散射及雷达散射截面，对雷达设计、目标识别、雷达成像等具有重要意义[1]。由于目标的电尺寸较大，采用矩量法(MoM: Method of Moment)[2-4]、有限元(FEM: Finite Element Method)[5-6]等数值方法计算电磁散射时，计算时间较长，内存需求较大，难以实现高效仿真。然而，高频电磁散射呈现一部分光学特性，因此可以利用光学特性进行近似，即采用物理光学(PO: Physical Optics)[7-8]方法实现电磁散射的高效求解。

不失一般性，假设三维目标表面用平面三角形建模，被剖分为个三角形面元。当采用物理光学方法计算高频电磁散射时，由于每个面元上的感应电流和磁流只由入射电磁波决定，使得计算复杂度为()。因此，物理光学方法是预估高频电磁散射的高效算法。但是目标表面并不是每个面元都存在感应电流和磁流。根据物理光学原理，目标表面仅有一部分被入射电磁波“照明”，剩下的部分即“阴影”区域[9]。被照明的区域存在感应电流和磁流，而阴影区域的感应电流和磁流为零。因此，在采用物理光学方法计算电磁散射时，首先需要判断照明和阴影区域。当目标表面被剖分为许多个三角形面元时，传统的判别方法是逐个判断每个面元是否被其余面元遮挡。该判别过程计算复杂度为(2)。当三角形个数非常多，即目标非常大时，遮挡判别的时间将非常长，将严重影响物理光学方法对散射场的求解。

本文首先分析了传统的遮挡判别方法，并在传统方法基础上，引入了树型结构和并行技术，从根本上实现了遮挡判别的提速。为了验证方法的正确性和高效性，本文利用新方法对飞机模型和坦克模型的遮挡关系进行了判别，并给出了相应的仿真结果。

1 高频RCS预估中的阴影判别原理

目标电磁散射的高频近似原理认为，目标被入射波照亮的部分会产生感应电流和磁流，目标未被入射波照亮的部分电流和磁流为零。因此，整个目标分为两个区域，照明区和阴影区。高频方法首先要把散射体模型的照明面和阴影面分离出来，该过程就是判别阴影面元。一个高效的自动判别算法既直接影响计算结果的精度，又可使计算过程更加快速。

为了判别阴影区域，先将整个过程分为单重和多重两类：如果某个面元仅仅是因为朝向，使得入射射线无法到达面元的外表面，从而被判断为阴影面，则称为该面元被单重遮挡；如果某个面元被判断为阴影面，其原因是它面元挡在该面元与入射波之间，则称该面元被多重遮挡。单重判别比较简单，只需要利用面元的外法向量和入射波的方向矢量即可，如图1(a)所示。

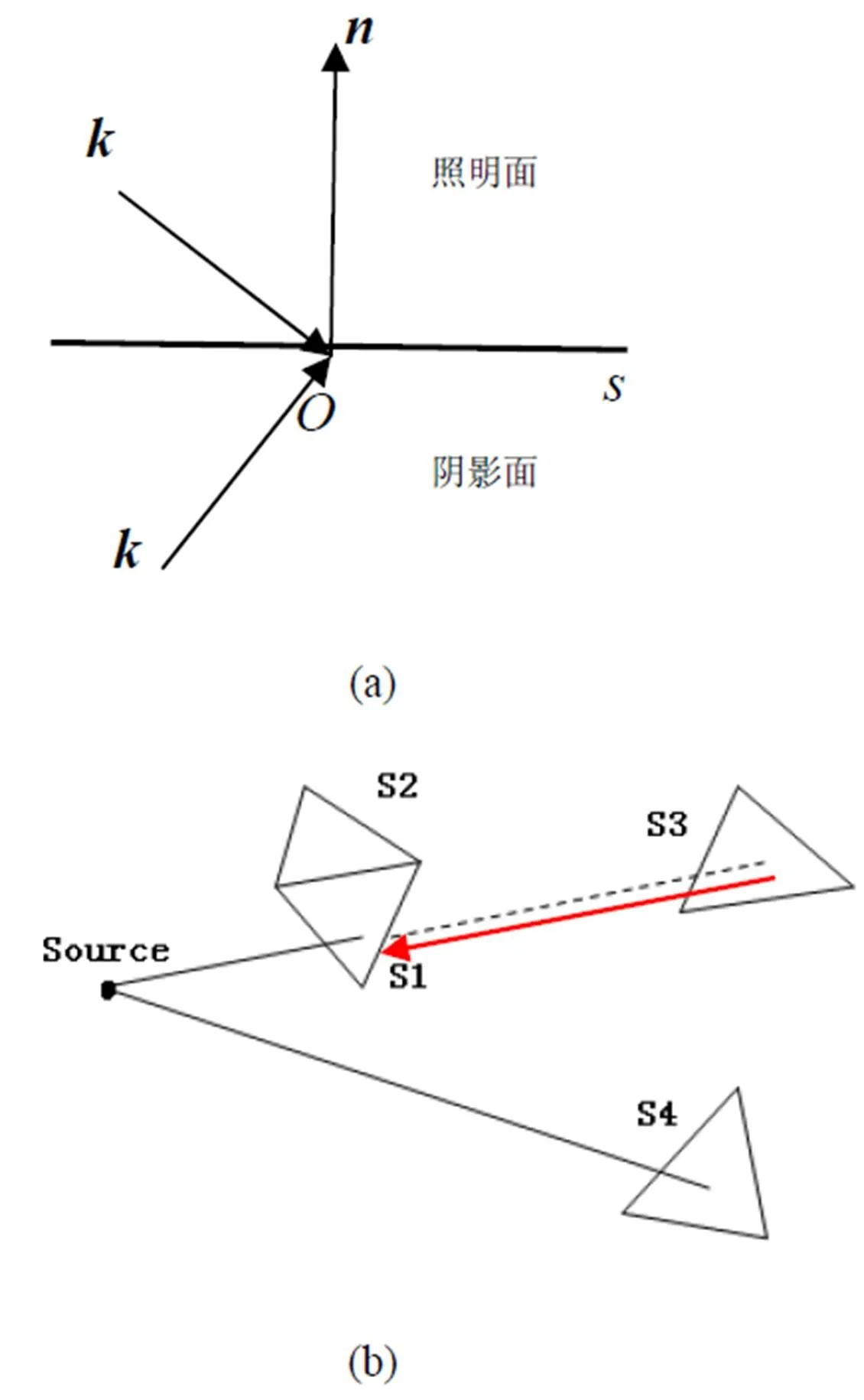
图1 高频散射中的遮挡：(a) 单重遮挡示意图；(b) 多重遮挡示意图

单重判别的运算过程简单，运算速度快。但单重判别只能用于几何体简单的情况。

对于多重判别，计算过程比单重要复杂，一般在单重识别后，对剩余的照明面元再进行处理。多重判别的示意图如图1(b)所示，假定此时面元1、2、3和4在单重判别的过程中被识别为照明面，下面分析3的多重判别过程。首先从面元3的中点引出一条射线，方向为入射波方向的反方向，从而将问题转化为分析该射线与其余面元是否有交点。依次判断该射线与各个面元是否有交点，如果有，则面元3被判断为阴影面；反之，面元3被判断为照明面。由此可见，要分析每个面元的遮挡关系，就需要从每个面元引出射线，再判断射线与所有的面元是否相交，当面元很多时计算量是巨大的。因此，研究快速算法非常必要。

2 基于树型结构的多重遮挡判别方法

多重判断的运算量主要集中在通过几何关系求解射线与面元之间的交点。经过单重判断后，假设有个面元被判定为照明，则多重判别的运算过程需要求解2次交点。对于电大尺寸目标，面元特别多，则多重判别过程就特别缓慢。为了加速这个过程，可以引入八叉树结构[10]。

2.1 基于树型结构的多重遮挡判别算法

图2 树型分组结构

计算射线与面元的交点时，可以先计算射线与分组的交点；若射线与某个分组没有交点，则该分组包含的所有面元都不会与该射线有交点；若射线与某个分组有交点，则依次计算该区域包含的所有面元与该射线的交点。通过这种分组的策略，大大降低了射线与面元求交的过程，提高了计算效率。对于更大规模的问题，可以通过多层的树型结构来加速。即判断出射线与某个分组有交点时，则进一步与该分组的子分组依次判断，直到子分组为最细层的分组为止，再对分组中的面元进行判断。其运算复杂度从传统方法的(2)降为(log)，对于电大尺寸目标，计算效率得到极大地改善。

2.2 利用并行技术对算法加速

在利用树型结构求解多重遮挡时，还可以引入并行计算技术。传统的串行策略，每次判断一条射线，个三角形单元，则需要判断次。采用并行技术后，求解所有面元引出的射线与面元的交点可以同时进行。假设机器的计算单元有个，则每次可以同时判断次射线。理论上的计算时间则将为原来的1 /，从而可以极大地节省计算时间。但由于并行效率不一定达到理想情况，实际的加速效果会比1 /要差一点。

3 数值算例

3.1 树型遮挡判别算法的效率分析

下面用两组数值算例来说明物理光学方法中遮挡算法的效率，模型分别是VFY-218和Tank，剖分的平面三角形面元个数分别是108600和335892。图3和图4分别给出了这两个算例的判别结果，途中深色部分表示照明区域，而途中浅色部分表示阴影区域，红色箭头表示平面波的入射方向。从图中可以看出，本文算法的正确性。表1给出了传统算法与基于树型结构的算法的计算时间，可以看出，引入树型结构之后，算法的效率极大提高。但随着树型结构层数的不断增加，计算时间先快速降低然后又升高，原因是分层数量不断增加，射线与面元之间的交点计算时间不断减少，但射线与子区域之间的交点计算时间逐渐增加，并逐渐成为计算的主要负担。

图3 VFY-218飞机的多重遮挡结果：(a) 顶部入射 (= 0°,= 0°)；(b) 侧面入射 (= 90°,= 90°)

Fig.3 Result of VFY-218：(a) Illuminated from top (= 0°,= 0°)；(b) Illuminated from side (= 90°,= 90°)

图4 Tank的多重遮挡结果：(a) 顶部入射 (θ = 0°, φ = 0°)；(b) 侧面入射 (θ = 90°, φ = 90°)

表1 传统多重遮挡方法和基于树型结构的多重遮挡方法比较(时间：秒)

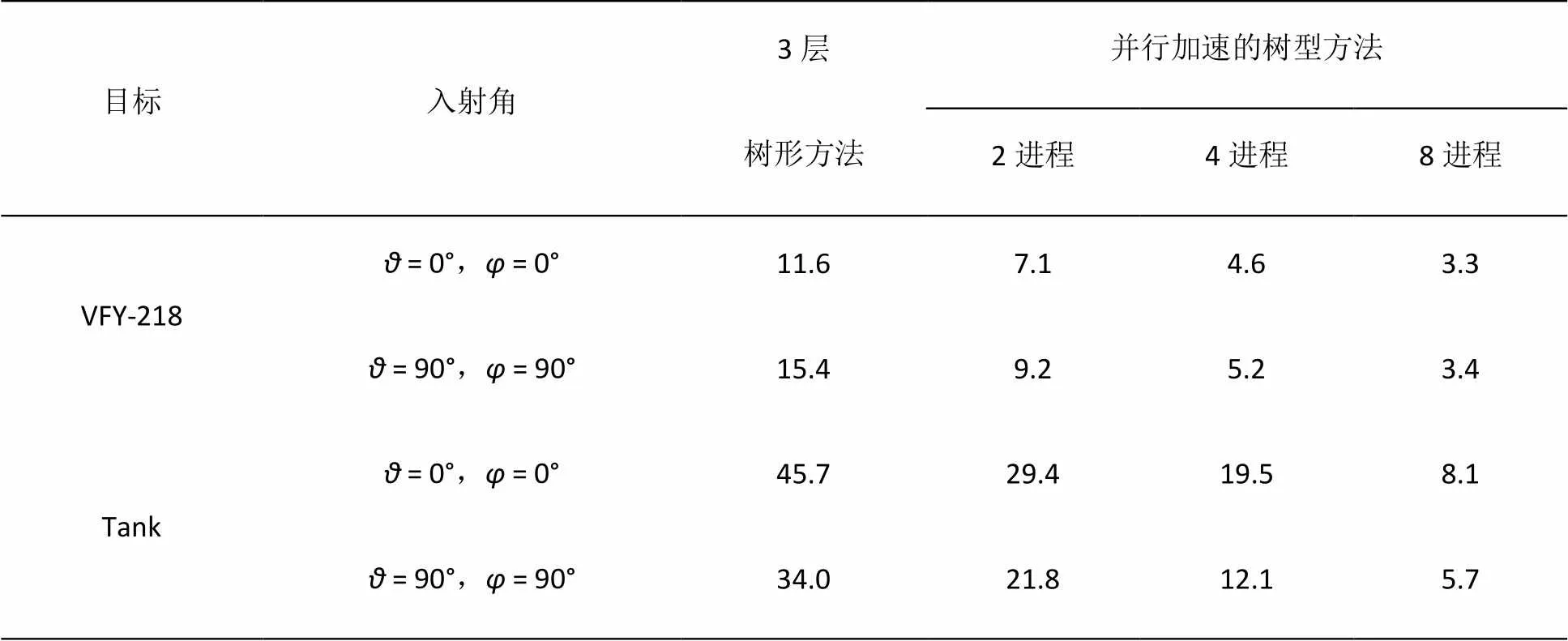
表2 串行方法与并行方法计算时间比较(时间：秒)

从表1中可以看出，基于树形结构的快速遮挡算法，可以极大地改善计算效率。然而，对于单站RCS计算、雷达回波数据仿真等问题，需要反复地判别遮挡区域，使得有必要寻求更多地方法对遮挡判别进行加速。随着计算机技术的发展，目前的PC机逐渐都是双核或四核处理器，使得在PC机上能够很容易实现并行算法。对于遮挡判别问题来说，由于每个面元的判别过程是独立于其它面元的，不存在前后的因果关系。因此，可以在树形结构加速的基础上，采用并行处理技术，对遮挡判别再次加速。下面列出采用并行技术后，VFY-218和Tank的遮挡判别时间。

3.2 算法并行化后的效率分析

表2中列举的树形结构为3层时，是否采用并行技术判别遮挡的计算时间比较。当采用并行技术时，进程数的选取分别为2、4和8。当采用的并行技术后，从表2中可以看出遮挡判断的时间显著降低。然而，随着进程数的不断增加，时间并没有按照反比的关系降低，原因是程序在执行过程中还存在着进程之间的通信，浪费了少部分时间。

4 结论

本文提出了一种基于树型结构的阴影区域识别方法，用于三维目标的高频电磁散射计算。该方法将利用树型分组结构将三维目标分为若干区域，从而将面元与面元之间的遮挡关系转变为面元与分组之间的遮挡关系。由于分组数目在数量级上远小于面元数目，因此本文提出的遮挡识别方法与传统方法相比，计算时间可以降低一个数量级。此外，本文还在树型结构的基础上，引入并行技术，在原有加速的效果上，再次减少计算量。树型结构和并行技术的结合使用，使高频电磁散射分析中的遮挡判别的计算量问题得到较好解决。飞机和坦克模型的数值算例也证明了本文提出的方法的正确性和高效性。

[1] Ascher U, Mattheij R, Russell R. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations [M]. US: Prentice-Hall, 1988: 100-120.

[2] Harrington R. Field computation by moment methods [M]. Malabar, Fla.: R. E. Krieger, 1968: 100-120.

[3] Chew W, Jin J, Michielssen E. et al. Fast and Efficient Algorithms in Computational Electro- magnetics [M]. Boston, MA: Artech House, 2001: 100-120.

[4] 张晓燕, 李子, 江代力,等. 随机粗糙面上电磁散射的高效迭代IEM计算[J]. 华东交通大学学报，2012, 25(3): 16-20.

[5] Chen R, Yung E, Chan C. et al. Application of SSOR preconditioned conjugate gradient algorithm to edge-FEM for 3-dimensional full wave Electromagnetic boundary value problems [J]. IEEE Trans. MTT., 2002, 50(4): 1165-1172, 2002.

[6] Chen R, Ping X, Yung E. Application of Diagonally Perturbed Incomplete Factorization Preconditioned CG Algorithms for Edge FEM Analysis of Helemholtz Equations [J]. IEEE Trans. AP., 2006, 54(5): 1064-1068.

[7] Knott E. A progression of high-frequency RCS prediction technique [J]. IEEE Proceedings, 1985, 73(2): 252-264.

[8] 刘志伟, 张月园, 陈嘉琪,等. 移变模式双站SAR信号模型及电磁仿真研究[J]. 华东交通大学学报，2012, 25(1): 24-29.

[9] F. Saez de Adana, Gonzalez I, Gutierrez O, et al. Asymptotic method for analysis of RCS of arbitrary targets composed by dielectric and / or magnetic matericals [J]. IEE Proc. Radar Sonar Navig., 2003, 150(5): 375-378.

[10] Liu Z, Ding D, Chen R. Octree based technique for fast analyzing shadowing relationship of complex target [C]. APMC, Hongkong, China. 2008.

[11] Lu C, Chew W. Fast algorithm for solving hybrid integral equations [J]. IEE Proceedings-H, 1993, 140(6): 455-460.

[12] Song J, Chew W. Multilevel fast-multipole algorithm for solving combined field integral equations of electromagnetic scattering [J]. Micro. Opt. Tech. Lett., 1995, 10(10): 14-19.

PARALLELED MULTIPLE SHADOW RECOGNITION ALGORITHM FOR EVALUATION OF HIGH FREQUENCY RCS

*ZHANG Yue-yuan1, LIU Zhi-wei2,3, ZHANG Xiao-yan2,3, LIU Ying-ting2, HE Shan2

(1. International School, East China Jiaotong University, Nanchang, Nanchang, Jiangxi 330013, China;2. School of Information Engineering, East China Jiaotong University, Nanchang, Jiangxi 330013, China;3. State Key Laboratory of Millimeter Wave, Southeast University, Nanjing, Jiangsu 210096, China)

Using physical optics method to evaluate high frequency radar cross section (RCS), the shadow recognition is required and time consuming. A tree structure based method is proposed for multiple shadow recognition. Judging whether a facet is obstructed by another facet is replaced by judging whether a facet is obstructed by another sub-group. The computational complexity is able to be reduced greatly by this method. Furthermore, the parallel technique is introduced. The computation time can be saved by the paralleled tree-base multiple shadow recognition algorithms. Numerical results demonstrate that the proposed method is more efficient than traditional method.

electromagnetic field; high frequency scattering; paralleled shadow recognize; computational electromagnetic; physical optics

O441.4

A

10.3969/j.issn.1674-8085.2013.04.009

1674-8085(2013)04-0041-05

2013-05-15；

2013-05-26

国家自然科学基金项目(61261005)；毫米波国家重点实验室 (K201326)；江西省科技厅青年基金项目 (20122BAB211018)；江西省教育厅青年基金项目(GJJ13321)

*张月园(1981-)，女，浙江金华人，讲师，硕士，主要从事计算机应用技术研究 (Email: aney0360_cn@sina.com);

刘志伟(1982-)，男，江西南昌人，讲师，博士，主要从事计算电磁学研究 (Email: zwliu1982@hotmail.com);

张晓燕(1979-)，女，云南楚雄人，副教授，博士，主要从事计算电磁学研究 (Email: xy_zhang3129@sina.com);

刘颖婷(1988-)，女，湖南冷水江人，硕士生，主要从事计算电磁学研究 (Email: yingtingmm@163.com);

何 姗(1989-)，女，安徽安庆人，硕士生，主要从事计算电磁学研究 (Email: lucky-shan@163.com).