多涡卷四阶Jerk系统的仿真研究

刘明华

多涡卷四阶Jerk系统的仿真研究

刘明华

(井冈山大学电子与信息工程学院，江西，吉安 343009)

对四阶Jerk系统中通过引入具有多个线性分段的锯齿波函数实现多涡卷混沌吸引子的机理进行了分析。在MATLAB中分别采用M语言和SIMULINK平台实现了多涡卷四阶Jerk系统的数值仿真，设计了多涡卷四阶Jerk电路，在EWB电路仿真软件中搭建了电路并进行了相关电路仿真。理论分析、数值仿真及电路仿真的相关结果一致，进一步证实了多涡卷混沌吸引子的存在。多涡卷混沌吸引子的存在，为混沌在信息安全中的应用提供了理论基础。

四阶Jerk系统；锯齿波函数；多涡卷混沌吸引子；仿真

0 引言

混沌行为是一种非常复杂的动力学行为，它具有对初始值的高度敏感性、不可预见性、内随机性和类噪声性[1-3]。正因为混沌具有这些特性，它在诸如保密通信领域、图像加密领域中有着广泛的应用前景。与单或双涡卷混沌吸引子相比，多涡卷混沌吸引子具有更多更复杂的动力学行和多个螺旋密钥参数[4]，在信息安全、保密通信等工程领域具有更好的应用前景，是目前混沌研究领域的一个热点课题[5-12]。

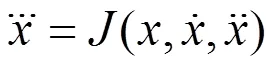
1 多涡卷形成机理分析

文献[5]在只能产生双涡卷混沌吸引子的四阶Jerk系统的基础上，通过引入具有多个线性分段的锯齿波函数()，使系统可以产生多涡卷混沌吸引子。多涡卷四阶Jerk系统的状态方程为

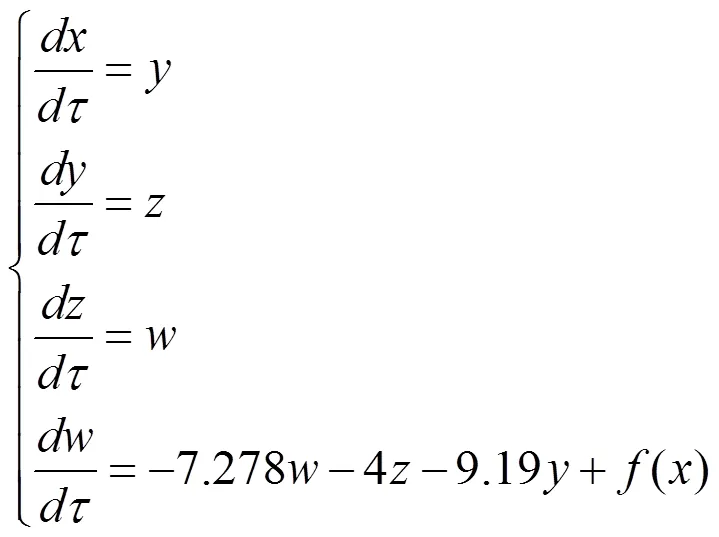
式中锯齿波函数()为

参数=7.9，＞ 0，≥ 1。参数A可以控制涡卷的大小，即A越小时涡卷就越小，在运算放大器的有限电压范围内能产生更多数量，反之A越大时涡卷就越大，在运算放大器的有限电压范围内能产生数量就受到限制。

令(1)式的左边为零，可知系统的平衡点方程为

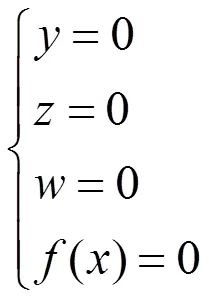
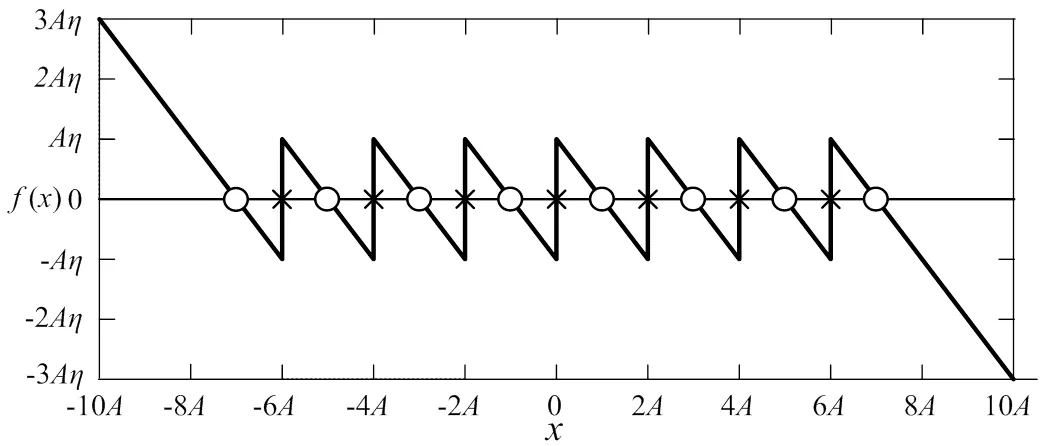
以=4为例，锯齿波函数()的平衡点分布如图1所示，图中符号“O”和“×”分别表示指标2和指标1的鞍焦平衡点。现在考察指标2的鞍焦平衡点对应的特征值。对应的Jacobian矩阵为

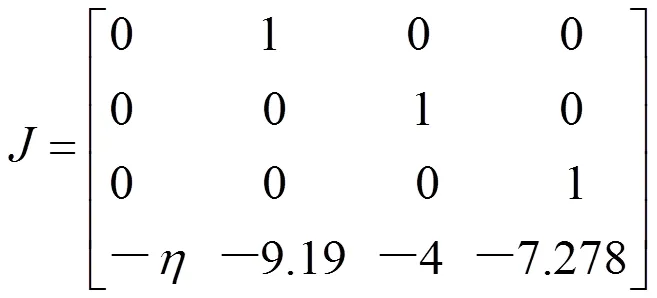
式中=7.9。得对应的特征值为λ1,2=0.18682± 1.1956i，λ3=-6.866，λ4=-0.78568。因而“O”表示的平衡点为指标2的鞍焦平衡点，每个鞍焦平衡点能产生一个涡卷，故图1所示的锯齿波函数()可产生8或9卷混沌吸引子。

2 多涡卷系统的MATLAB仿真

MATLAB是一种面向科学与工程计算的高级语言，将数值分析、矩阵计算、科学数据可视化及非线性动态系统的建模和仿真等强大功能集于一体，为科学研究、工程设计等提供一种全面解决方案，具有极高的编程效率。值得注意的是，MATLAB中还集成了SIMULINK，它提供了图形编辑器、可自定义的定制模块库以及和求解器，便于进行动态系统建模和仿真[15]。

下面以8涡卷混沌吸引子为例，分别采用M语言和SIMULINK平台这两种不同方法实现系统(1)的数值仿真。这时系统(1)的状态方程可改写为

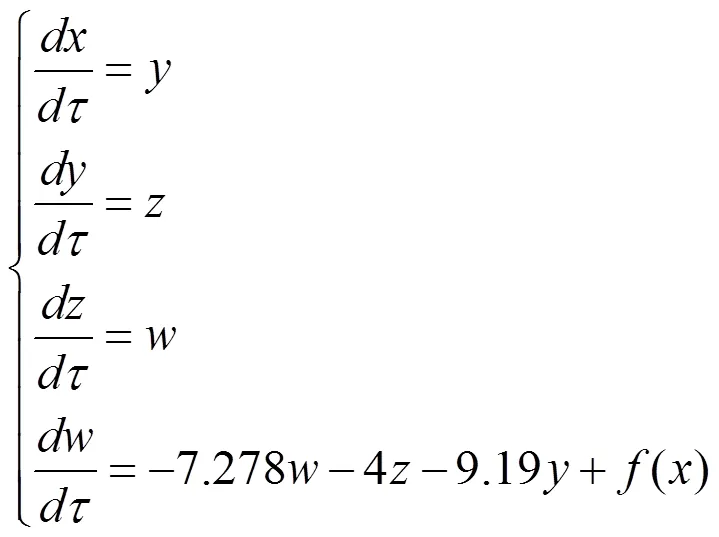
式中() = -+[sgn() + sgn(-2) + sgn(+2) + sgn(-4) + sgn(+4) + sgn(-6) + sgn(+6)]，参数=7.9，=1。

采用M语言来实现的步骤为：(a)根据(4)式的微分方程，建立相应的函数文件。

function dxdt=Jerk_multiscroll(t,x)

eta=7.9; A=1; b=9.19; c=4; d=7.278;

f=-eta*x(1)+eta*A*(sign(x(1))+sign(x(1)-2*A)+

sign(x(1)+2*A)+sign(x(1)-4*A)+sign(x(1)+4*A)+

sign(x(1)-6*A)+sign(x(1)+6*A))；%锯齿波函数

dxdt=[x(2);x(3);x(4);-b*x(2)-c*x(3)-d*x(4)+f];

(b)调用微分方程求解函数ode45。

t0=[0 1e+3]; %仿真时间

x0=[0.1, 0.27, 0.3, 0.4]; %系统初始值

[t,x]=ode45(' Jerk_multiscroll ',t0,x0,options);

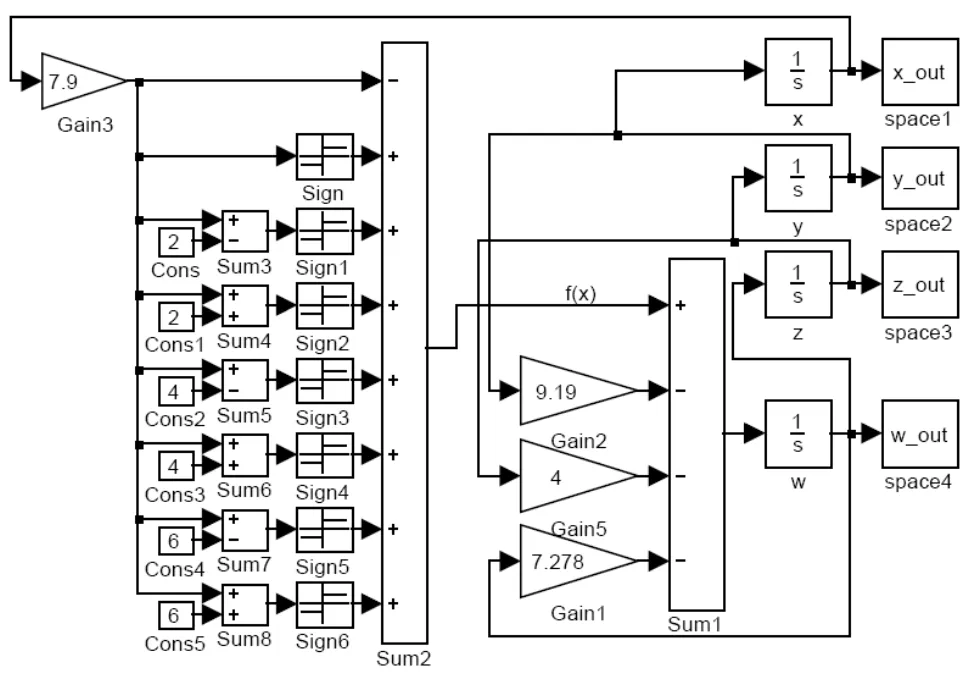
图2 8涡卷四阶Jerk系统的SIMULINK仿真图

基于SIMULINK平台的动态仿真步骤为：(a)先用SIMULINK模型库构建仿真系统。根据系统(4)的状态方程特点，将所需要用到的单元功能模块(积分模块、求和模块、增益模块以及实现符号函数的模块Sign)拖放到平台搭建窗口，并按系统(4)的状态方程把各模块连接起来，搭建好的仿真系统如图2所示。(b)设置系统的初始值及仿真时间。在此，初始值为设置为(0.1, 0.2, 0.3, 0.4)，仿真时间为200s，其它参数为默认。用XY graph观察混沌吸引子相图，观察到的8涡卷混沌吸引子数值仿真结果如图3(a)所示，采用类似方法可搭建9涡卷的SIMULINK仿真系统并进行相关的数值仿真，仿真结果如图3(b)所示。

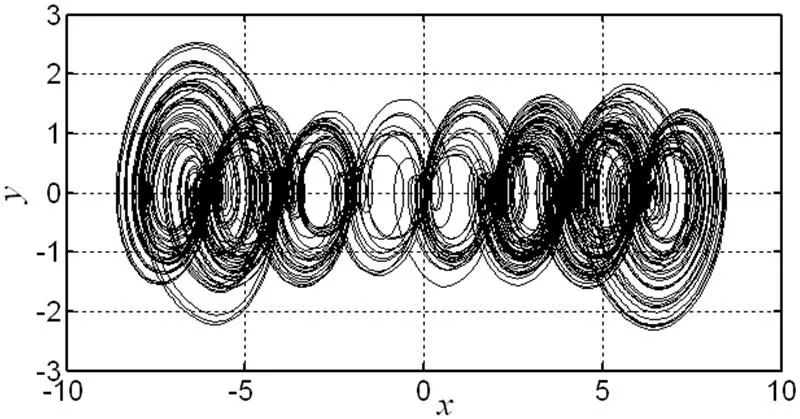
(a)

(b)

图3 数值仿真结果 (a)8涡卷; (b)9涡卷

Fig.3 The results of numerical simulation (a)8-scroll; (b)9-scroll

3 电路仿真

根据系统(4)的状态方程，设计了一种可以产生8涡卷混沌吸引子的四阶Jerk电路，如图4所示。整个电路由两大模块组成，分别为实现非线性函数-()的N1模块和实现系统(1)中的微积分函数的N2模块，其中N2模块又是由反相比例加法电路、积分电路和反相电路组成。

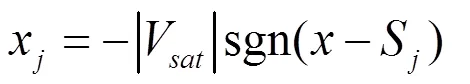
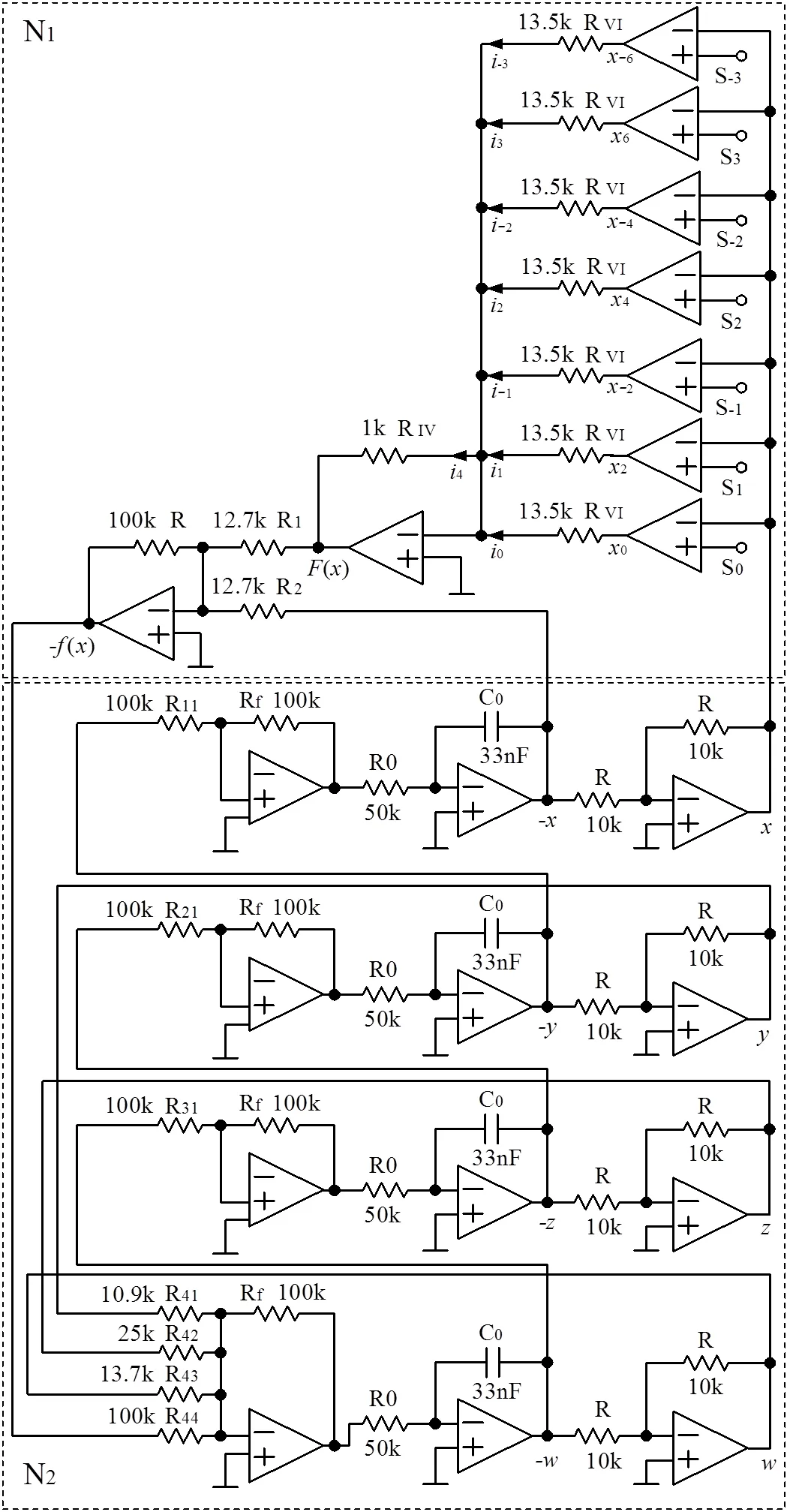
图4 8涡卷四阶Jerk电路图

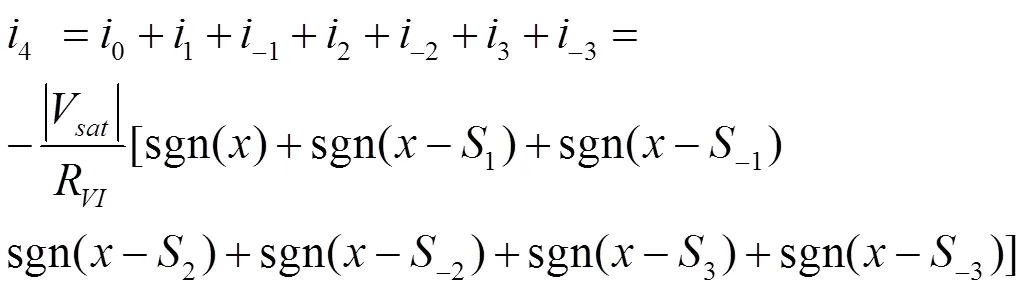
再将电流转换为电压，可以得到

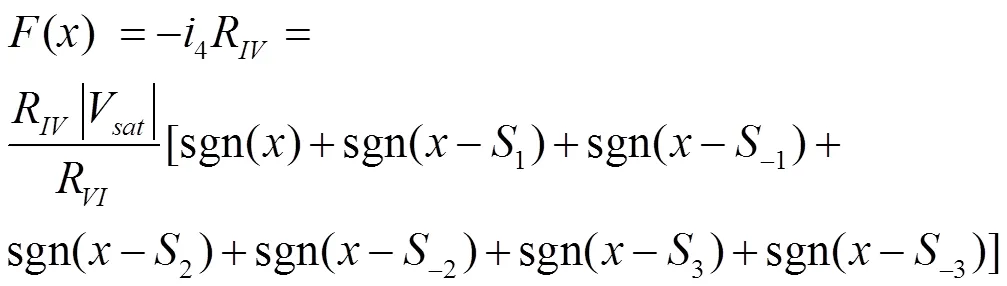
故非线性函数-()的状态方程可表示为

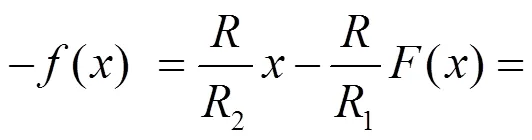
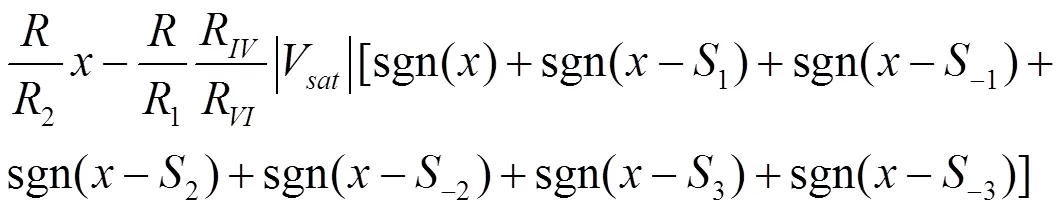
当=4，=7.9，=1，可产生8多涡卷混沌吸引子的锯齿波函数()的表达式为

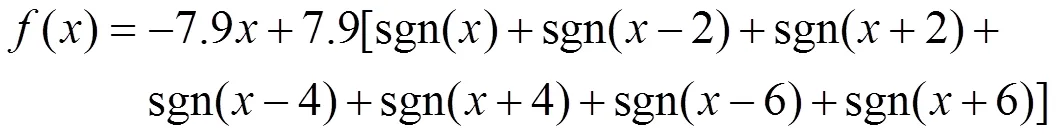
在N2中，可以推导出电路对应的状态方程为

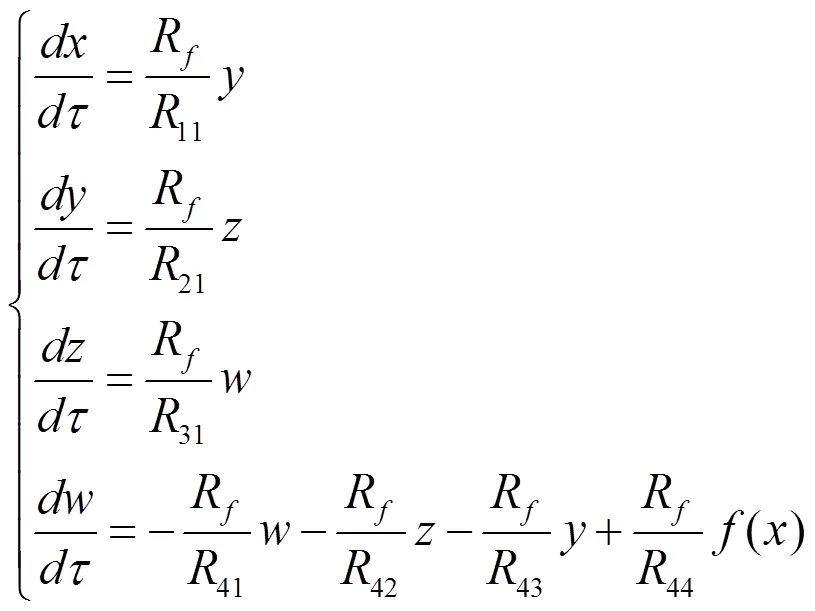
(a)

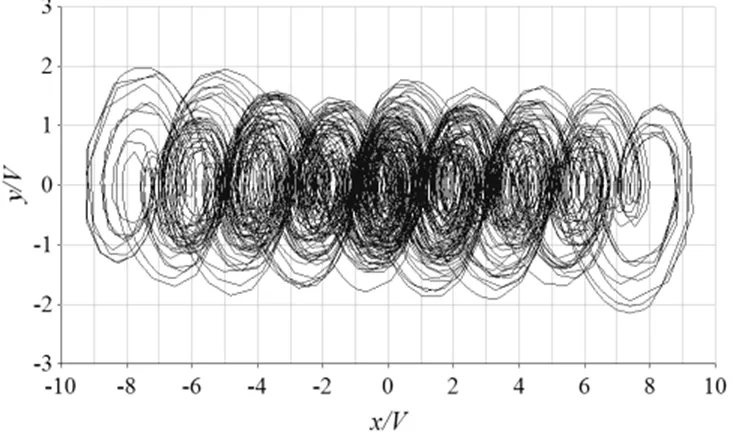
(b)

4 结论

本文采用M语言和SIMULINK平台实现了多涡卷四阶Jerk系统的数值仿真，更进一步，在EWB电路仿真软件中搭建了多涡卷四阶Jerk电路并进行了相关电路仿真，数值仿真与电路仿真结果一致，证实了多涡卷混沌吸引子的存在，为其在信息安全中的应用提供了理论基础。本文采用的有关数值仿真和电路仿真方法具有普适性，可以推广到其它混沌系中。

[1] 王梓坤. 论混沌与随机[J]. 北京师范大学学报:自然科学版,1994, 30(2):199-202.

[2] Chen Guanrong, Yu Xinghuo. Chaos control: Theory and applications[M]. Berlin, Heidelberg: Springner- Verlag, 2003.

[3] 陈关荣, 吕金虎. Lorenz系统族的动力学分析、控制与同步[M]. 北京: 科学出版社, 2003.

[4] 禹思敏. 混沌系统与混沌电路—原理、设计及其在通信中的应用[M]. 西安: 西安电子科技大学出版社, 2011.

[5] 刘明华, 禹思敏. 多涡卷高阶广义Jerk电路[J]. 物理学报, 2006, 55(11):5707-5713.

[6] 张朝霞, 禹思敏. 用时滞和阶跃序列组合生成网格多涡卷蔡氏混沌吸引子[J]. 物理学报, 2009, 58(1):120-130.

[7] 包伯成, 刘中, 许建平, 等. 基于Colpitts振荡器模型生成的多涡卷超混沌吸引子[J]. 物理学报, 2010, 59(3):1540-1548.

[8] 晋建秀, 丘水生. 基于物理混沌的混合图像加密系统研究[J]. 物理学报, 2010, 59(2):793-800.

[9] 刘金梅, 丘水生，刘伟平. 基于超混沌系统的图像加密算法的安全性分析[J]. 计算机应用研究, 2010, 27(3):1042-1045.

[10] 王静,蒋国平.一种超混沌图像加密算法的安全性分析及其改进[J].物理学报,2011,60(6):60503-1-060503-11.

[11] 刘慧杰, 冯久超, 任斌. 开环全光混沌通信系统中的光纤信道结构[J]. 光子学报, 2012, 41(11):1267-1273.

[12] Yu Simin, Lü Jinhu, Yu Xinghuo, et al. Design and Implementation of Grid Multiwing Hyperchaotic Lorenz System Family via Switching Control and Constructing Super-Heteroclinic Loops[J]. IEEE Trans. Circuits and Systems-I, 2012, 59(5):1015- 1028.

[13] Sprott J C. Simple chaotic systems and circuits[J]. Amer. J. Phys., 2000, 68(8):758-763.

[14] Chlouverakis K E, Sprott J C. Chaotic hyperjerk systems[J]. Chaos, Solitons and Fractals, 2006, 28: 739-746.

[15] MATLAB及在电子信息课程中的应用[M]. 3版. 北京: 电子工业出版社, 2006.

SIMULATION INVESTIGATION MULTI-SCROLL FOUR-ORDER JERK SYSTEM

LIU Ming-hua

(School of Electronics and Information Engineering, Jinggangshan University, Ji’an, Jiangxi 343009, China)

The mechanism of generating multi-scroll chaotic attractors which can be obtained by introducing sawtooth function based on four-order Jerk system is analyzed. Some numerical simulations of multi-scroll chaotic attractors are realized by M language and SIMULINK platform in MATLAB. A novel multi-scroll four-order Jerk circuit is designed. The circuit is built on Electronics Workbench (EWB) platform, and circuit simulation is experimented. Theoretical analysis, numerical simulation results and circuit simulation results are agreed, which confirmed the multi-scroll chaotic attractors exist. The existing of multi-scroll chaotic attractors provides the theoretical basis for the application of chaos in information security.

fourth-order Jerk system; sawtooth nonlinear function; multi-scroll chaotic attractor; simulation

TN710；TN918

A

10.3969/j.issn.1674-8085.2013.04.012

1674-8085(2013)04-0059-05

2013-02-18；

2013-05-20

江西省教育厅科技项目 (GJJ13542)；井冈山大学自然科学基金项目 (JZB1203)

刘明华(1975-)，男，江西吉水人，副教授，博士，主要从事非线性电路与系统研究(E-mail:liuminghua2000@sina.com).