覆盖粒计算的新模型

张 辉，王丽华，李令强

覆盖粒计算的新模型

*张 辉，王丽华，李令强

（聊城大学数学科学学院，山东，聊城 252059）

基于覆盖重新定义了Zoom-in算子，通过Zoom-in算子和Zoom-out算子的不同复合分别得到论域及粒化了论域上的近似算子，并将它们与拓扑中的预内部算子、闭包算子建立联系。此外还详细讨论了它们的性质。

粒计算；Zoom-in算子；Zoom-out算子；近似算子；粒化

0 引言

粒计算是近十年发展起来的一门新学科。它以姚一豫提出的粒计算三元论(即多视角、多层次粒结构和粒计算三角形)为基本研究框架，从哲学、方法论、信息处理三个侧面进行结构化思维、结构化问题求解、结构化信息处理的深入探究，并吸纳、提炼及抽象各个学科中粒处理思想，以期建立系统的、与具体学科知识无关的粒计算原理，从而指导人类问题求解和实现机器问题求解[1-2]。在粒计算中，粒是基本概念之一。现实生活中，人类在处理大量复杂信息时，由于人类认知能力有限，往往会把大量复杂信息按其各自特征和性能将其划分为若干较为简单的块，每个被分出来的块就被看成是一个粒。实际上，一些个体通过不分明关系、相似关系、邻近关系或功能关系等所形成的块就是粒。我们通常把划分粒的过程称为信息粒化。通过粒化，人类获得对客观世界和主观世界多层的描述与理解。目前关于粒计算已有众多的研究成果，例如，粗糙集与粒计算的交叉问题的研究、基于相容关系的粒计算模型及其在进化计算﹑机器学习和数据挖掘中的应用等[3-7]。这些成果的取得及相关理论的研究对人工智能和相关的问题求解理论等都有重要的应用前景。

粒计算模型主要有3种：词计算模型、粗糙集模型和商空间模型。一些学者在此基础上又提出了许多新的模型，其中，折延宏等人和王国朋等人先后基于覆盖找到了两类不同的粒计算模型[8-9]。其中，文献[9]使得粒化得到的信息更加丰富，从而进一步拓宽了基于覆盖的粒计算模型的应用范围，但是，有时通过这个模型得到的信息对我们的研究是毫无意义的。

于是，本文重新定义了Zoom-in算子，给出了一种基于覆盖的粒计算新模型。经过这个模型得到的信息较文献[9]更加精确，而较文献[8]得到的信息更加丰富。然后，对Zoom-in和Zoom-out算子进行复合分别得到论域及粒化了论域上的近似算子，并详细讨论了它们的性质。与此同时，将它们与拓扑中的预内部算子、闭包算子建立了联系。下面，回顾一下有关的基本概念和定义，其中未提及的符号均来自文献[10]。

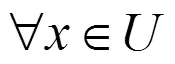
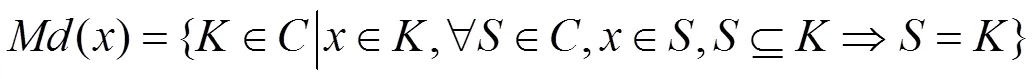
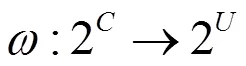
则称为一个Zoom-in算子。

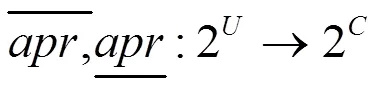
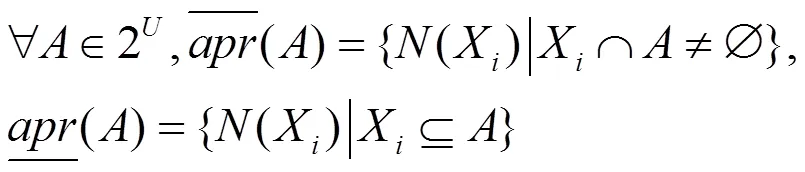
注记：这里的X有双重身份，它既是论域的子集，又是有限覆盖的一个元素。为了区别起见，采用了Yao在文献[12]中的表示方法。用(X)表示是覆盖的一个元素，而用X表示论域的子集。

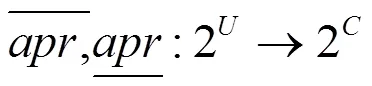
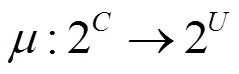
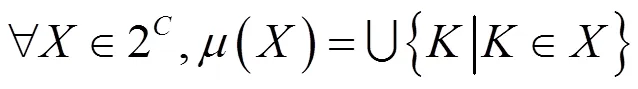
则称为一个Zoom-in算子。

1 基于覆盖的粒计算新模型

以上SHE YH和WANG GP都基于覆盖找到了两种不同的粒计算模型。在本节中，我们找到了一种新的基于覆盖的粒计算模型，并采用与上述文献不同的方式重新定义了Zoom-in算子。

则称为一个Zoom-in算子。

下面的例子说明了，本文定义的Zoom-in算子与定义1、定义3中的Zoom-in算子是不相同的。

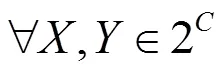
证明 性质(1)显然成立。

(3)由(2)立得。

下例说明性质(2)的逆命题不成立。

2 论域上的近似算子与

由式(2)及式(4)可得，

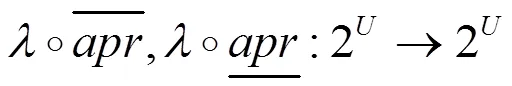
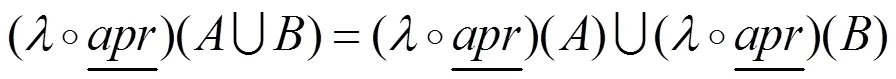
证明：由性质1及性质2可得证。

由定义5及性质3可得：

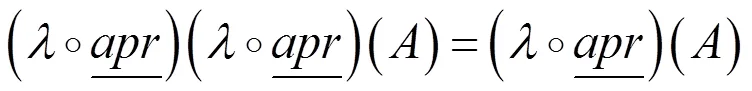
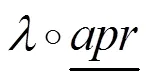
3 粒化论域上的近似算与

性质4 设为一个非空论域，为一个有限覆盖，则

证明：由性质1、性质2以及上述定义容易证得。

由上述定义及性质可得：

推论3 设是非空论域，是上的一元典型覆盖，则

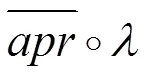
4 结论

本文通过利用元素邻域重新定义Zoom-in算子找到了不同于文献[8，9]的基于覆盖的粒计算新模型。本文还将Zoom-in和Zoom-out进行了重新复合，得到了论域及粒化了的论域上的近似算子，并将它们与拓扑中的预内部算子、闭包算子建立了联系，同时详细讨论了它们的性质。但是，如何将这两个近似算子与Galois联络联系起来还有待我们继续研究。

[1] 姚一豫.粒计算三元论[M].北京:科学出版社,2010: 115-143.

[2] Yao J T.Novel Developments in Granular Computing: Applications for Advanced Human Reasoning and Soft Computation[M].Information Science Reference, Herskey, PA2010:1-15.

[3] Lin T Y. Granular computing on binary relations I: Data mining and neighborhood systems[C]. In: Skowron A,P- olkowski L, eds. Rough Sets in Knowledge Discovery. Heidelberg: Physica-Verlag, 1998:107-121.

[4] Lin T Y. Granular computing on binary relations II:Rough set representations and belief functions[C].In:Skowron A, Polkowski L, eds. Rough Sets in Knowledge Discovery. Heidelberg: Physica-Verlag ,1998:121-140.

[5] Ma J M, Zhang W X, Li T J. A covering model of granular computing[C]. In: Proc. of the 2005 Int’l Conf. In Mac- hine Learning and Cybernetics.2005:1625-1630.

[6] Wang G Y, Hu F, Huang H, Wu Y. A granular computing model based on tolerance relation[J].The Journal of China Universities of Posts and Telecommunications, 2005, 12(3):86-90.

[7] Zhang L, Zhang B. The quotient space theory of problem solving[J].Fundamenta Informaticae,2004,59(2-3):287- 298.

[8] She Y H, Wang G J. Covering Model of Granular Computing[J]. Journal of Software, 2010, 21(11) : 2782- 2789.

[9] 王国朋,王程.一种新的粒计算的覆盖模型[J].聊城大学学报:自然科学版,2011,24(4):34-36.

[10] Yao Y Y. A partition model of granular computing[J]. Lecture Notes in Computer Science, 2004,3100:232-253.

[11] Bonikowski Z, Bryniarski E ,Wybraniec-Skardowska U. Extensions and intentions in the rough set theory[J]. J-ournal of Information Sciences, 1998,107:149-167.

A NEW COVERING-BASED MODEL OF GRANULAR COMPUTING

*ZHANG Hui, WANG Li-hua, LI Ling-qiang

(School of Mathematics Science, Liaocheng University, Liaocheng, Shandong 252059, China)

Based on covering, a new Zoom-in operator is presented. Furthermore, a new model of granular computing is investigated. Different rough approximations of the universe of discourse and granulated universe of discourse are obtained by different combinations of Zoom-in and Zoom-out operators. Then we established the relation that they and topology of preliminary internal operator, closure operator. In addition, their properties are discussed in detail.

granular computing; Zoom-in; Zoom-out; approximation operator; granulated

O159.1

A

10.3969/j.issn.1674-8085.2013.04.001

1674-8085(2013)04-0001-04

2012-12-18；

2013-03-23

国家自然科学基金项目(61273044)

*张 辉(1989-)，男，山东济宁人，硕士生，主要从事模糊拓扑学研究(E-mail:cxzhanghui@16.com);

王丽华(1988-)，女，山东济宁人，硕士生，主要从事拓扑学研究(E-mail:1615288127@qq.com);

李令强(1980-)，男，山东济南人，讲师，博士，主要从事拓扑与序结构研究(E-mail:lilingqiang@126.com).