小学高年段数学审辨式教学的思考与实践

蒋巧君

（浙江省义乌市宗泽小学）

发展学生的数学审辨思维，对培养他们的问题解决能力和创造性思维具有重要的作用。一个具有数学审辨思维能力的人，在面对不同情境时，能够勇于质疑、理性分析、不断反思，得出合理结论，提出有效解决方案。

在教学中，既不能忽视学生数学审辨思维的发展与培养，又不能过高地估计他们审辨思维品质发展的水平。我们要分析、综合由审辩式思维派生出的抽象、概括、比较、分类、具体化和系统化等思维过程，根据不同年龄段学生的思维特点，引导他们通过实践这些过程，达到培养审辩式思维的目的。在低年段，要根据学生具象化思维为主的特点，引导他们直接观察，选择的培养方向应尽量简单。在高年段，则要根据学生处于抽象逻辑思维发展加速期和独创性思维开始具备的特点，开展数学审辨式教学。小学高年段申辩式教学，可以围绕“高认知审辨”进行“质疑批判、分析论证、综合生成、反思评价”，防止“策略性思维”的学习任务下降到“技能”甚至是“记忆”的水平。我们认为，在小学高段开展的审辨式教学，重点应是设计数学审辨思维层次评价单，难点是提炼会有理有据地进行分析论证，要点是形成凸显数学审辩思维要素的课堂教学样态。我们采取了如下的实施策略。

一、研发数学审辨思维层次评估单

根据SOLO分类理论，教师在课前应认真设计好“审辨学习层次评价单”。在审辨式教学的整个过程中，可以根据课程的重难点有选择地考评每个学生在某一板块的数学审辨思维层次水平。在审辨式教学中，学习层次水平评估单的内容要突显审题、提问、探索和反思等重点，并在课后评估每个学生的数学审辨思维层次和反思，进行后续教学的思考。下面呈现的是“‘烙饼问题’数学审辨思维层次评估单（教师用）”的综合表。（如表1）

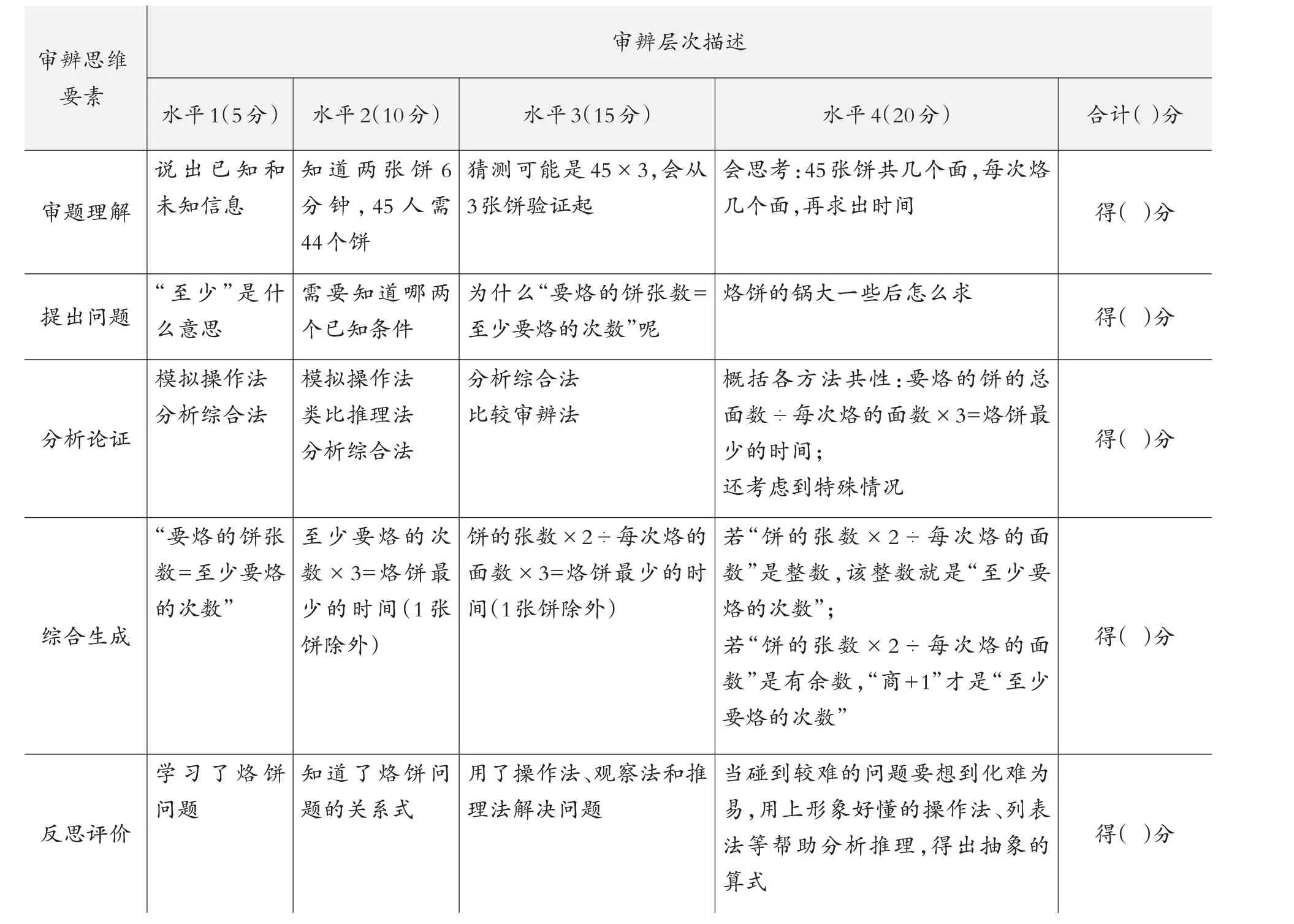
表1 “烙饼问题”审辨思维层次评估单（教师用）

二、提炼有理有据分析论证的内联式策略

小学高段数学的审辨式教学指向“分析、评价和创新”高级认知目标，在引导学生质疑批判的同时，培养学生有理有据分析论证的能力。借助比较形象的“操作模拟法、画图列表法、实验验证法”等可见思维，学习用“假设法、倒推法”等特殊方法找到解题的突破口，突出“分析综合法、比较审辨法、抽象概括法”这一系列具有内联式关系策略的培养，促使学生自主揭示客观事物的本质特征和内部联系，以提高小学高年段学生对已有知识经验的改组、建构能力，而不是只按现成的方案和程序直接解决问题。（如图1）

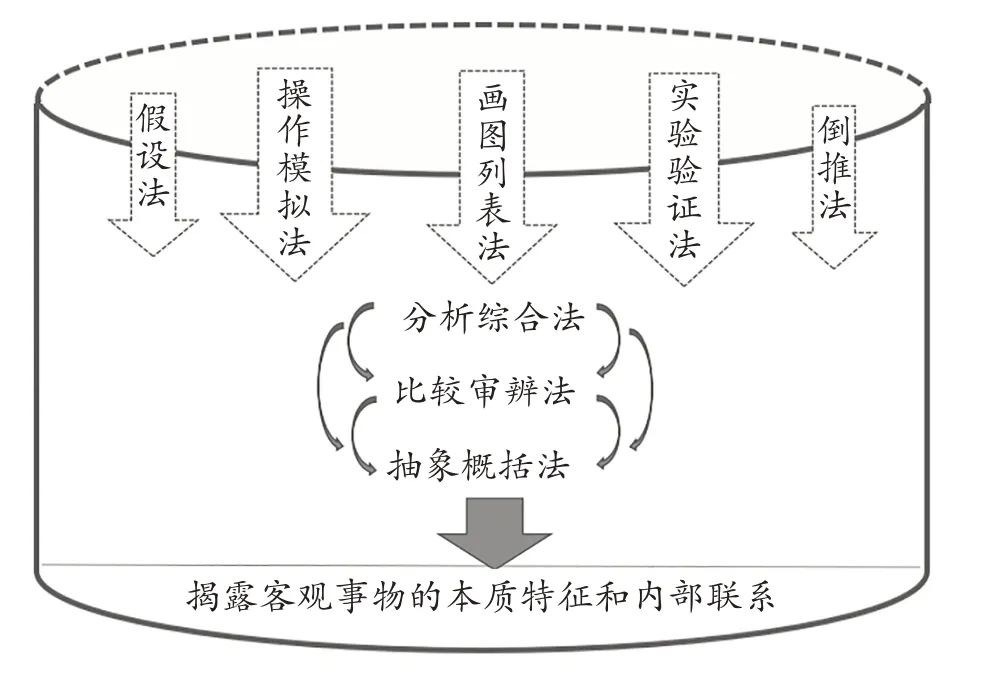
图1 有理有据分析论证的内联式策略图示

（一）分析综合法

“分析综合法”又叫混合分析法，是同时从已知条件与结论出发，寻找它们之间的联系而沟通思路的方法。在解题过程中，分析法和综合法是统一的，不能把分析法和综合法孤立起来使用。分析和综合相辅相成，有时先分析后综合，有时先综合后分析，有时会同时“两头兜”。如“烙饼问题”中的分析综合过程。（如图2）

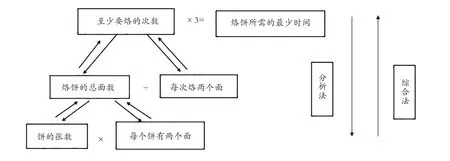
图2 “烙饼问题”分析综合过程

（二）比较审辨法

比较是在思想上把各种对象和现象加以对比，确定它们之间的相同点、不同点及其关系。比较是以分析为前提的，只有在思想上把不同对象的部分特征区别开来，才能进行比较。同时，比较还要确定它们之间的关系，所以比较又是一个综合的过程。比较是重要的思维方法，因为有比较才能有鉴别，只有通过比较才能找到事物的共同特征和差异点，才能正确地确定活动的方向。

如“烙饼问题”中的比较审辨过程。（如表2）

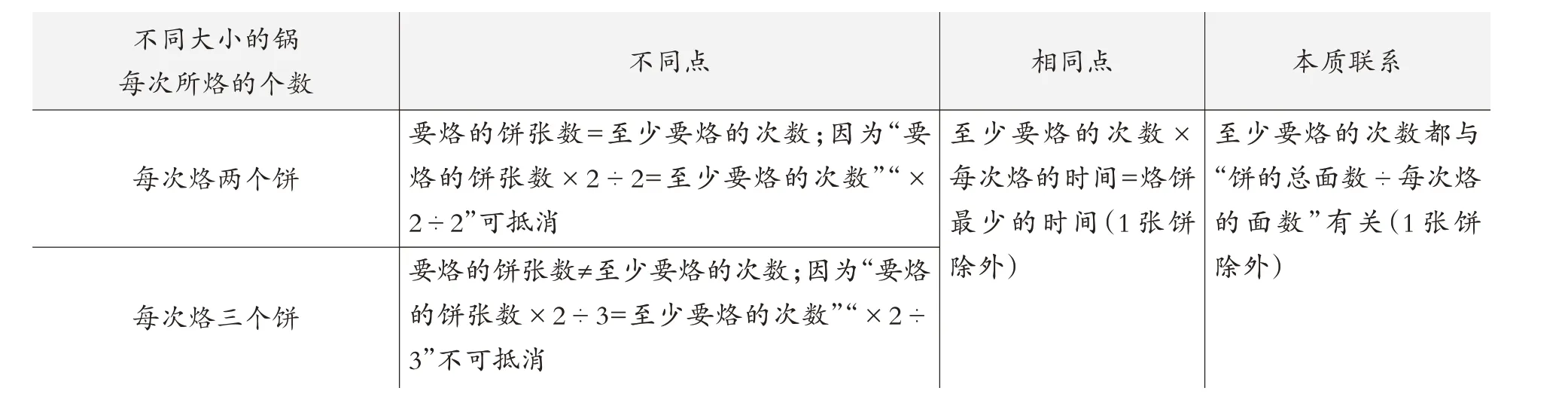
表2 “烙饼问题”中的比较审辨过程

（三）抽象概括法

先抽象再概括。所谓抽象是指在思考过程中，从具体的客观事物中抽取出其本质特征，而摒弃非本质特征的思维活动。数学抽象有利于认识事物的本质、认识一般性事物、认识数学中的无限、认识数学应用的广泛性。概括是把抽象出来的若干事物的共同属性归结出来进行考察的一种思维方法。概括要以抽象为基础，它是抽象的发展，是一种特殊形式的综合。概括是思维活动能迅速进行迁移的基础。如抽象概括“烙饼问题”中各方法的共性之处：要烙的饼的总面数÷每次烙的面数×每次烙的时间=烙饼最少的时间。在概括之后便于正向迁移，活学活用：若“饼的张数×2÷每次烙的面数”是整数，该整数就是“至少要烙的次数”；若“饼的张数×2÷每次烙的面数”是有余数的，“商+1”才是“至少要烙的次数”。

从图3中可知，学生从原有知识经验出发，经历“分析综合法、比较审辨法、抽象概括法”这一系列具有内联式关系的策略之后，才能得到“新的思维成果”。反思整个思维过程是具有探究性、审辨性的，而不是把现有答案或程序技能化。

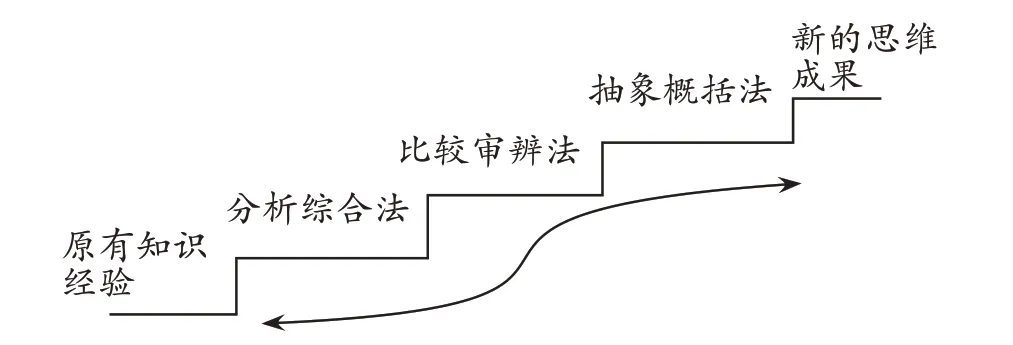
图3 学生数学思维形成过程

三、形成凸显数学审辨思维要素的课堂教学样态

根据数学审辨思维的四要素，我们形成了下面这样的审辨式教学流程图。（如图4）因为审辨思维始于质疑，归于反思，包括质疑批判、分析论证、综合生成、反思评价四个要素，是一个循环往复的过程。要让学生面对问题解决，不断地经历思考方法、积累思考方法、获取思考方法、应用思考方法。

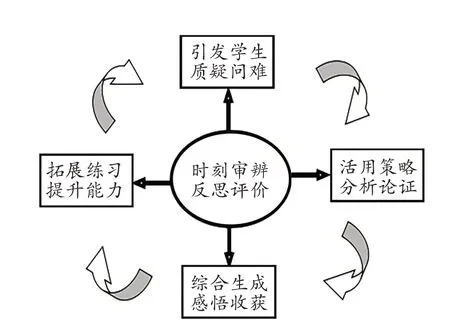
图4 审辨式教学流程

在审辨式教学对话过程中，师生之间设问、追问、反问成为新常态。培育数学审辨思维的要诀是：教师善于在困惑之处不懈追问，引导学生在争议之处双向质疑，在追问与质疑之处用证据说话。

师生之间可以主动运用“因为……所以”“如果……那么”“不仅……而且”“我猜想……经验证，得出结论”“我认为……依据是”等体现逻辑推理的关联词思考问题和交流分析问题，使小学高年段学生数学思维的深刻性、广阔性、批判性和自我控制的水平获得迅速发展。通过日积月累，学生逐渐就能养成数学审辨式思维的表达方式，也能养成言语推理的习惯。

根据审辨式教学中不同大问题的“高认知任务”，可以把审辨式教学主要分为三种课型：再造型审辨课、比较型审辨课和拓展型审辨课。

（一）再造型审辨课

探究性的“高认知学习任务”是指让学生经历再创造的主要来自于教材例题的新知。这些新知是属于教材中有现成的方法、原理或程序进行解答的常规数学问题，但对学生而言，是面临新的问题情境又缺乏现成对策的新知。我们一般用“疑-析-评-联”的审辨流程，让学生经历再创造的过程。这样的课型，我们称之为再造型审辨课。（如表3）

表3 再造型审辨课流程

教师的教是为了以后的“不用教”，学生的学是为了以后的“会自学”。有时，我们要求小学高年段学生在课前能主动自学，填写质疑卡和感悟卡。学生在自学过程中，充分经历独立思考和判断反思过程，这就是一个很好的审辨过程。

（二）比较型审辨课

辨析性的高认知学习任务是指易错易混的变式性问题，这类题能够刺激非常规的解决方法和触发学生的创新思维。这种常规问题的变式型高认知任务，一般的教学流程为“变-辨-辩-编”，这样的课型，我们称之为辨析性审辨课。（如表4）

表4 比较型审辨课流程

我们基于学情精心编制了易错、易混、内容较难的审辨精练册。审辨精练册由“审辨内容、审辨缘由、审辨难点、解题方法、解题思路、审辨过程”组成。此外，我们还将《易错易混审辨册》编制成微课，如“圆周长的一半和半圆的周长”“速度的平均数与平均速度”等易错、较难内容辨析探究，使学生在“尝试探索、辨析论证和发现规律”中慢慢提升审辨思维能力。

（三）拓展型审辨课

拓展性的“高认知学习任务”是指基于教材但拓展延伸的非常规问题。解决这类问题不能只靠一个简单明确的情境，而是需要创造性思维并应用一系列基于认知策略理解问题的情境来找到方法。这种非常规问题的“高认知任务”，要给学生思考时间，让他们慢慢地去发现、去拓展。一般的教学流程为“探—立—破—再立”，这样的课型，我们称之为一小时拓展型审辨长课。（如表5）

表5 拓展型审辨课流程

如“二十四点的秘密”“包装的学问”“百变正方体”等数学审辨思维含金量较高的课，可以让学生充分经历“分析综合法、比较审辨法和抽象概括法”，深挖细究，积累、获取并应用审辨思维方法解决非常规问题。我们还设计了学生就地取材的《审辨探索册》，引导他们从实际生活中发现数学问题、积极探索并解决问题，培养了学生独立思考和问题解决能力，提升了高阶思维水平。

总之，我们基于审辨思维“质疑批判、分析论证、综合生成、反思评价”的四要素，精心设计高认知水平的审辨任务。通过“初审三思、再审二找、终审悟法”这三大环节，引领学生导读审辨式任务、导学审辨式勾连、导引审辨式迁移，根据课时目标需求而灵活使用审辨学习层次评价单，开展审辨层次的评估。学生在审题质疑、独立思考后学会理解别人的解法，比较不同方法并优化解法，概括提炼后拓展延伸。这样，促进了学生的认知从单点结构向拓展结构发展，逐渐形成了“独立思考，不懈质疑，分析论证，有理有据，及时反思，正向迁移”的小学高年段数学审辨式教学新样态。（如图6）

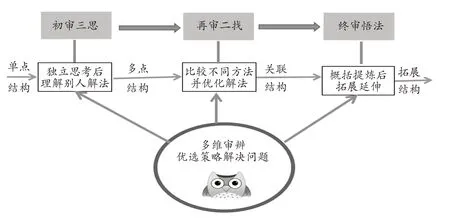
图6 用数学审辨思维解决问题的教学实践路径