小学数学深度学习的样态初探

邵明雪

摘要：关于深度学习的内涵与特征，不少研究者作出过解读，其中有一些高频词，如理解、迁移、应用、批判性、高阶思维等。基于学段定位，结合学科特征，探究小学数学深度学习的样态：注重知识迁移，着重数学理解，强调学以致用。

关键词：深度学习;小学数学;知识迁移;数学理解;学以致用

关于深度学习的内涵与特征，不少研究者作出过解读。苏州大学付亦宁博士认为：“深度学习是以内在学习需求为动力，以理解性学习为基础;运用高阶思维批判性地学习新的思想和事实;能够在知识之间进行整体性联通，将它们融入原有的认知体系进行建构;能够在不同的情境中创造性地解决问题;能够运用元认知策略对学习进行调控，并达到专家学习程度的学习。” 西北师范大学安富海教授认为：“深度学习是一种基于理解的学习，是指学习者以高阶思维的发展和实际问题的解决为目标，以整合的知识为内容，积极主动地、批判性地学习新的知识和思想，并将它们融入原有的认知结构中，且能将已有的知识迁移到新的情境中的一种学习。”上海师范大学黎加厚教授认为：“深度学习的三大特点是理解与批判、联系与构建、迁移与应用。”虽然界定不一，但出现了一些高频词：迁移、理解、应用、批判性、高阶思维等。這些关键词，给一线教学实践以清晰的指引。基于学段定位，结合学科特征，笔者尝试围绕迁移、理解、应用三个维度，探究小学数学深度学习的样态。

一、注重知识迁移

数学知识的迁移在小学数学学习中非常普遍。教学中，我们经常引导学生使用类比等手段，找到知识间的关联，对已有的知识结构进行重组，再加入新认知，形成新的知识结构。根据数学教育心理学的特点，迁移有方向性，可分为水平迁移和垂直迁移。

（一）水平迁移

水平迁移指逻辑关系并列的知识在学习间的相互影响。

比如，在学习图形的面积时，当学生掌握了长方形的面积公式后，其他图形的面积公式都可以此为基础推导出来：可以将长方形面积公式中的长和宽都代换为边长来推导正方形的面积;可以用“割补”的方法转化为长方形，从而求出平行四边形面积;可以用2个相同的三角形拼成平行四边形，来推导三角形的面积公式。总而言之，都是通过联想，在已有的知识经验基础上生成新的知识。

那如何使学生自主获得水平迁移？以《梯形的面积》教学为例，可设计如下小组活动：

1.观察梯形，思考并猜想：梯形的面积可能会跟哪种图形的面积有关？

2.根据猜想，可以用提供的梯形拼一拼、剪一剪、折一折。

3.变化后的图形是什么？将它的面积和原来的梯形相比，你有什么发现？

4.想一想，怎么求出梯形的面积？

这样设计，是因为学生已有长方形、正方形、三角形和部分组合图形面积的探究经验，所以小组活动的每个任务都强调知识的迁移过程：第1个任务，需要回顾已学过的图形面积知识，唤起相关图形记忆;第2个任务，需要借鉴已有的活动经验，并将之用于本节课的操作活动中;第3个任务，勾连新图形和原有图形;第4个任务，建构新的认知。通过这样递进的学习活动，学生自主习得梯形面积公式，借助迁移实现了深度学习。

（二）垂直迁移

垂直迁移主要是在概括性和抽象性上处于不同层次的数学学习之间的相互影响。

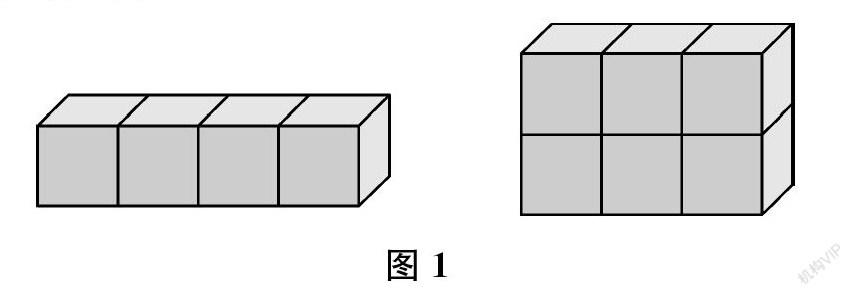
比如，很多学生通过课前学习，都知道“长方体的体积=长×宽×高”，但知其然而不知其所以然。同样是图形的学习，在学习“平面图形的面积”时，我们是使用1平方厘米的小正方形作为测量工具，通过测量不同的长方形，进而观察、归纳出长方形的面积公式。那么在学习长方体的体积公式时，这样的经验完全可以迁移过来用以探索立体图形的体积。

通过图1中2个长方体体积大小的比较，学生认识到长方体的体积和体积为1立方厘米的小正方体的个数有关。这时，有学生就想到：这和四年级学习长方形的面积计算有点像，把长方形换成长方体，小正方形换成小正方体就可以了。借着学生的思路，教师鼓励学生思考：怎么探究长方体的体积？

学生通过小组讨论得出探究步骤：

1.用不同的小正方体搭不同形状的长方体，记录长、宽、高、体积等数据。

2.观察长方体的长、宽、高、体积和小正方体个数之间的关系。

3.讨论长方体的体积公式。

其中，后两步完全是由长方形的面积公式探索经验迁移得来的，但是第一步，学生在经验基础上有所改进——探索长方形的面积时，长方形是给定的，但长方体没有办法直接给定，所以在探索时可以改变一下，直接用小正方体来搭建不同的长方体。

整个探究过程都由学生设计操作完成，形成经验，教师只需从旁帮助引导。这样的学习，解放了教师，让学生站在了课堂的中央;更重要的是，让学生在形成“双基”的基础上，有效迁移探究活动经验，实现深度学习。

二、着重数学理解

对数学知识的理解可简称为“数学理解”。目前对“数学理解”的若干研究聚焦于建立对数学概念、规则和方法的内部理解网络，数学理解水平的个体层次性，以及数学理解的认知结构和知识意义的建构过程。所以“数学理解”不是静态的，而是要形成知识体系的，要深层次地、动态地、批判地理解。

比如，思维导图是学生表达数学理解的一个形象化方式。利用思维导图对学习的数学知识进行归纳和总结，要求学生对数学知识有深入理解和掌握，包括理解算法背后的算理、理解知识的结构体系、理解数学的思想方法。通过组织学生自主梳理思维导图，可以帮助他们对知识进行系统归纳，促进学生的自主学习能力和思维能力的提高。

以《因数与倍数》单元复习课为例，借助思维导图开展教学主要分为三步。第一步：准备思维导图。在授课前一天的“助学单”上，布置梳理单元知识并形成思维导图的任务。第二步：小组解读思维导图。先由小组第一位成员解读自己的思维导图，再由组内其他成员进行补充和纠正，同时在第一位成员的思维导图上进行修改，直至所有成员补充完毕。第三步：全班解读思维导图。请一个小组解读自己小组完成的思维导图，由其他小组补充、评判、分析，也可以分享不同的思维导图。第四步：完成本单元知识梳理。

思维导图的应用，有助于学生以中心词为起点发散思维，根据知识之间的连接进行联想，从而建构知识网络。同时，在与他人交流、辨析的过程中，不断发散和丰富思维，深化数学理解。

三、强调学以致用

能否运用所学的知识解决生活中的问题是检验学生是否真正学会知识的重要标准。深度学习要求学生能够从生活情境出发，自主建构数学模型并获得解决问题的经验。所以在教学中，教师要引导学生将生活中的问题数学化，并将教学内容和生活情境合理关联，提高学生实践知识的可能性。

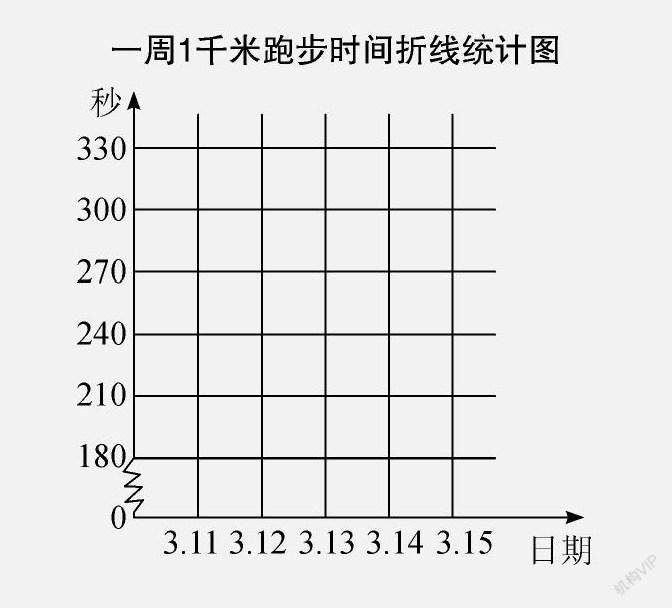
比如，学习《折线统计图》时，有学生认为，可以利用折线统计图表示事物变化的特点，将自己每天的跑步时间记录下来，用来观察自己跑步的变化情况。教师引导学生根據自己的需求探讨相关统计图的设计。通过讨论，学生制作出《一周1千米跑步时间折线统计图》，其中，折线统计图的横轴记录跑步日期，竖轴记录跑步所用时间。但竖轴每格表示多少，又成了争论的焦点：竖轴每格表示的时间既不能过长，以免统计数据过于笼统;也不能过短，以免统计数据太过烦琐。最后，经过商定，学生将竖轴每格的时间定为30秒，并且从3分钟后开始记录成绩，得到图2。

接下来的一周，学生每天坚持跑步并记录。一周后，教师询问：“通过一周的观察，之前的折线统计图有没有需要改进的地方？”学生迫不及待地举手回答：“我觉得可以缩小竖轴的范围。通过一周的实验发现，我们的成绩在短期内基本上都是在一个很小的时间段里，比如，我的成绩都在4分钟左右，所以可以把竖轴的时间范围设定在3分半到4分半，然后每格表示10秒，这样就更精确了。”“一周的时间太短了，看不出进步。我们可以把时间拉长一些，如3个星期或者一个月，这样变化才能更明显。”就这样，学生根据自己的实际情况，改进了自己的跑步时间折线统计图，深化了对折线统计图的理解和运用。

在这样的学习中，学生不仅需要解决相关的问题，同时也需要考虑各种随着事件发展而产生的新问题，并要构思新的解决方案，而这其中关系到的信息都需要学生自己去选择和分析。这在很大程度上提高了学生的思维质量和问题解决水平，学生也在不知不觉中达成了深度学习。

参考文献：

[1] 付亦宁.深度学习的教学范式[J].全球教育展望，2017（7）.

[2] 安富海.促进深度学习的课堂教学策略研究[J].课程·教材·教法，2014（11）.

[3] 何玲，黎加厚.促进学生深度学习[J].现代教学，2005（5）.

[4] 曹才翰，章建跃.数学教育心理学[M].北京：北京师范大学出版社，2006.