指向数学大概念的问题设计

夏繁军 常丽 艳尤飞

摘要：指向数学大概念理解或感悟的教学应该是问题驱动式的，这样的教学具有学习评价伴随性的特征。大概念是更加抽象、上位的概念，因此，需要更加开放、综合的问题来教学和评价。而大概念又是在具体知识、技能基础上的抽象概括，因此，开放、综合的问题也要能够细化、分解。在实践中，提取数学大概念后，主要通过多元化的方式设计（选取）指向数学大概念理解或感悟的问题，具体包括：开放探源，设计单元或课时基本问题;综合应用，设计单元探究问题;步步为营，设计课时引导性问题;目标分解，设计课时诊断性问题;以生为本，捕捉课堂生成性问题。

关键词：数学大概念;问题设计;大概念教学;大概念评价

卡尔·波普尔认为：“知识的增长永远始于问题，终于问题——越来越深化的问题，越来越能启发大量新问题的问题。”学习的过程本质上是解决问题的过程，也是学习如何解决问题的过程。无论是教师提出问题，还是学生发现问题，问题都是促使学生学习进程发生和发展的不竭动力。问题有启发性，学生能在解决问题的过程中不断理解知识的本质，明确思考的逻辑。问题还有导向性，能够引导学生有目的地组织有效的方法策略，利于学生建构学习内容之间的联结。

《普通高中数学课程标准（2017年版2020年修订）》（以下简称“课标”）在“教学建议”中指出：“基于数学学科核心素养的教学活动应该把握数学的本质，创设合适的教学情境、提出合适的数学问题，引发学生思考与交流，形成和发展数学学科核心素养。”数学核心素养是抽象概括出来的、比较上位的、具有广泛联系整合作用的、能够广泛迁移应用的数学概念和观点，是一种数学大概念。因此，指向数学大概念理解或感悟的教学，也应该是问题驱动式的，或者说是启发引导式、探究发现式的。这样的教学具有学习评价伴随性的特征：教师提出的问题，既促进学生的学习，又起到评价学生学习情况的作用。也就是说，教学和评价很大程度上是一体的。

大概念是更加抽象、上位的概念，需要更加开放、综合的问题来教学和评价。而大概念又是在具体知识、技能基础上的抽象概括，开放、综合的问题也要能够细化、分解。此外，大概念贯穿于多个内容，因此，还需要持续性教学和评价。在实践中，提取数学大概念后，我们主要通过以下方式设计（选取）指向数学大概念理解或感悟的问题。值得注意的是，这些问题有时是交叉的，就像连续光谱一样不好区分。

一、开放探源，设计单元或课时基本问题

基本问题是指在学科或课程中处于核心位置、能促进学生深入思考和探究、能激發知识的联系和迁移的总结性问题或单元（多个相关联的内容所形成的整体）的主题性问题。威金斯和麦克泰格将基本问题比作大概念教学的航标：“最好的问题是指向和突出大概念的。它们就像一条过道，通过它们，学习者可以探索内容中或许仍未被理解的关键概念、主题、理论、问题，在借助启发性问题主动探索内容的过程中加深自己的理解。”在他们的单元整体设计模板中，基本问题和大概念是相配套的。珀金斯则直接称基本问题为“大问题”。

如果说传统的问题倾向于“闭合性”，也就是对固定答案的寻求，那么，基本问题恰恰相反，倾向于“开放性”。因此，基本问题能引发与大概念相关的持续性思考，不断激活具体经验，达成深度理解。比如，语法是怎么产生的？为什么会有语法？汉语的语法和英语的语法有什么区别？数学是发明，还是发现？某个数学概念为什么这么定义？由此定义能够得到什么？……有时，基本问题甚至会带有一些“挑衅性”，通过连续的追问打破学生原有的观点，引导学生深入思考，建立复杂的认知结构。此外，基本问题也可以是一个话题（主题），主要是引导学生往“大处”想。

基本问题具有本源性与整合性，是单元教学的“魂”，往往会在单元教学开始时提出，牵引学生进行单元学习。单元教学结束时，可再让学生根据本单元的学习回答基本问题。原来谜底在这儿！原来基本问题的答案是它！这些应该是学生学完一个单元后的体会。如果没有这样的感觉，那就说明教师的教学有待改进。

例如，《函数》单元教学，基本问题可以是：你如何理解函数是描述两个变量之间关系最基本的数学语言（工具），或者函数是一个量随另一个量变化而变化的模型？什么是函数的性质？如何研究函数的性质？为什么要研究函数的性质？函数发展历史是怎样的？你怎么看待函数？……还可以在学生学完函数的概念和表示、函数的性质、幂函数、指数函数、对数函数、三角函数等内容后，让他们再回答这些问题。

又如，《概率》单元教学，可以提出这样的基本问题：现有5个签，其中2个签有奖，5个同学先后来抽签，每人抽一个，那么中奖机会均等吗？这个问题学生熟悉，答案在给定条件下不唯一，能引起学生的争论，直指大概念“随机性”“事件的关系与运算”。教学样本空间、随机性、事件的关系与运算等内容时，都可以用。

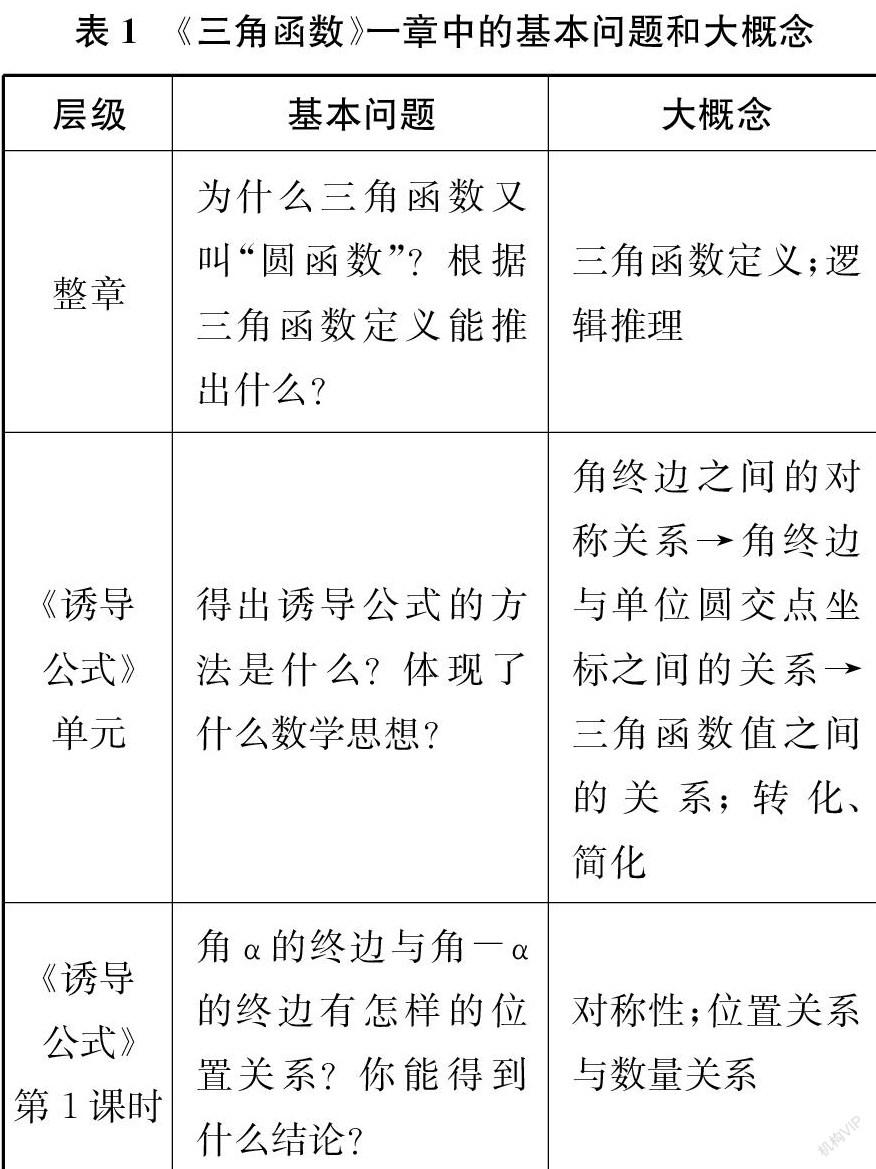
此外，大概念的层级性决定了基本问题的层级性。例如，《三角函数》一章中基本问题和大概念存在对应关系（如表1所示）。

二、综合应用，设计单元探究问题

基本问题和探究问题都具有复杂性。但是，相对而言，基本问题偏向本源，因开放思辨而比较“虚”——答案不确定;探究问题偏向应用，因综合实践而比较“实”——完成比较难。因此，基本问题可以用于单元教学的开头和结尾，而探究问题主要用于单元教学的结尾。课标附录2中给出的“教学与评价案例”大多是比较典型的探究问题。这些探究问题通常是对课时学习内容的综合应用，可以促进学生的深度学习，让学生持续理解大概念。

例如，《统计》单元教学后，教师让学生分组选择一个感兴趣的问题，给出一份完整的统计分析案例。比如，对人们线上、线下生活消费数额与年龄的关系，刹车距离与车速的关系，学校近三年男生和女生平均身高、体重情况（学校医务室有数据可用）等，利用统计的方法进行分析，然后作出合理的决策。课外，学生尝试探究;课上，师生交流遇到的问题。在完成这个探究问题（任务）的过程中，学生学会把调查到的社会现象数据化，设计调查问卷，抽样调查，分析整理数据，分析变量之间的相关性分析。

再如，“指数函数”（《基本初等函数Ⅰ》单元）以及“极限”（《导数》单元）教学后，教师让学生在知道复利计算公式[y=a（1+r）x，x∈N*]，以及本息和随存款期数呈指数型增长的基础上，研究相同的本金和存款总时间、总利率下不同复利分期带来的不同本息和（分期的利率等于总利率除以期数）。进而引导学生发现：随着复利分期的增加，本息和也在增加，但是增加得越来越缓慢，并且好像趋向一个常数。然后，教师让学生做一个极端的假设，即本金为1，总利率为100%，研究本息和随复利分期的变化趋势;并让学生借助计算器或计算机完成计算，引导他们发现：当n趋向于+∞，（1+1/n）n趋向于定值2.71828…。由此，介绍自然对数底数的由来，同时让学生感悟“在一定的局限条件下，凡事多有极限，不会无限增长，不会‘永动”的大概念。

三、步步为营，设计课时引导性问题

学生对基本问题的思考很难一步到位，而且常会觉得无从下手。对此，在具体的课时教学中，教师要准确把握教学内容，精准分析学情，设计层层递进的引导性问题（串），启发学生抽丝剥茧，有逻辑地思考，不断理解与感悟、逐步揭示数学大概念。

例如，面面平行的性质定理研究的是两个平面平行的条件下，直线与平面、直线与直线的位置关系的不变性，思想方法是从一般到特殊。这是个大概念。对此，在课时教学中，提出如下引导性问题串：

问题：类比线面平行的研究，我们研究面面平行的性质定理，首先要弄清楚：面面平行的性质定理研究的是面面平行的条件下，谁与谁的位置关系的规律性或不变性？

追问1：先看两个平面平行时，一个平面内的任一条直线与另一个平面的位置关系。如图1，已知α∥β，lCα ，判断l与β的位置关系。

追问2：再看两个平面平行时，分别在两个平面内的两条直线的位置关系。如图2，已知α∥β，lCα，mCβ ，判断l与m的位置关系。

追问3：平面β内与l平行的直线有多少条？

追问4：如何在平面β内找出一条与l平行的直线？

追问5：类比线面平行性质定理的发现，在平面β内取一点P，过点P如何作直线l的平行线？

追问6：任作一个平面与α、β相交于两条直线，这两条直线是否平行？

整个研究过程贯彻数学大概念“从一般到特殊、从整体到局部的方法”。对于追问4，在学生想不到过l作平面γ与平面β相交，从而找到直线m的情況下，追问5可以为学生建构面面平行的性质定理搭建“脚手架”：当学生看到直线与直线外一点时，容易联系线面平行的性质定理，作平面γ与平面β相交。

四、目标分解，设计课时诊断性问题

引导性问题既可以用于教学，也可以用于评价。诊断性问题主要用于评价（即课堂检测，也可以看作是教学的一部分，因为还是服务于教学的），可以采用定性与定量（如口头访谈与书面测试）相结合的方式，实现了解学生的学习情况（对大概念的理解或感悟），指导教师精准教学（以学定教、因材施教），提高教学效率的目的。具体设计诊断性问题时，要特别注意依据抽象、上位的教学目标进行细化分解，从而提升评价的有效性和可行性。

例如，课标对“函数的单调性”的学习要求是：“借助函数图像，会用符号语言表达函数的单调性、最大值、最小值，理解它们的作用和实际意义。”仅依据此，很难编写诊断性问题。

对此，初步细化分解时，可以聚焦大概念，考虑到底想要学生掌握什么，用自己的话稍加详细地转述。仔细分析上述目标要求，从知识结果上看，是要学生理解单调性的定义，会用定义证明函数的单调性，会用单调性解决一些数学问题;从方法过程上看，是让学生掌握抽象概括的方法和运算求解的技能。但是，这时还是较难编写具体的诊断性问题。

对此，进一步细化分解时，就要考虑操作性，如怎么才算理解函数的单调性、怎么才算简单应用函数的单调性，将目标要求变成一个个外显的、有层次的操作行为。比如，可以通过具体化行为动词和核心概念，以及适当添加行为条件，把“理解函数的单调性”由浅到深地分解为：（1）能从学过的函数中举出具有单调性的例子;（2）能用自己的话概括描述函数单调性的含义;（3）能对照函数图像求出函数的单调区间;（4）能在教师的启发下抽象出函数单调性的符号表示，结合具体问题体会到函数单调性定义的要点;（5）能用定义证明一些简单函数的单调性。

其中，第1个目标和第2个目标本身就可以当作诊断性问题。对于第3个目标，教材和课后练习中都有相关的题目可以作为诊断性问题。对于第5个目标，教材中有相关的例题可以作为诊断性问题。第4个目标中，对概念要点的理解很关键：学生自己常常认识不到;而且有时，教师给学生写出“几点注意”，学生也不理解为什么。因此，教师要设计好诊断性问题，让学生在问题情境中认识单调性定义的要点。具体地，可以设计如表2所示的诊断性问题。

五、以生为本，捕捉课堂生成性问题

课堂是一个充满生机和活力的地方，学生经常提出一些我们始料未及的问题。这些问题是学生的疑点，有时也是我们进行数学大概念教学和评价的契机。

例如，学习“平面向量基本定理”时，学生提问：“基底是什么？”对此，教师反问：“对于‘基底，大家如何理解？生活中有没有类似的例子？”在学生的沉默思考中，教师提示：“同学们学过绘画吗？”一些学生恍然大悟：“底色，三基色！”顺势，教师解释：“五彩缤纷的颜色可以通过红、绿、蓝三色按照不同的比例合成产生，同样，绝大多数单色光也可以分解成红、绿、蓝三种色光。这是色度学最基本的原理，即‘三基色原理。三种基色是相互独立的，任何一种基色都不能由其他两种基色合成。基底{e1，e2}就是平面向量中的基色。”进而，教师引导学生从数学到其他领域展开关于“基底”的联想：

平面坐标系内一点P由两个坐标（x，y）决定;等差数列{an}由公差和首项决定;圆由圆心和半径决定……

汉字复杂多样，但是基本笔画只有几种;音乐美丽动听，但是基本音调只有几个……

小到个人，大到国家，都有自己的基底。一个人的基底就是这个人的德、智、体、美、劳;一个国家的基底可以从政治体制、经济实力、军事力量、外交政策、科技水平这几个角度反映出来，更能从国民的一言一行中反映出来。

基底思想是一个大概念，体现简化和转化的意识。对学生疑问的反馈，既能帮助学生深度理解概念，也能对学生进行思想品德教育。

再如，指数函数应用的复利计算问题：“有些银行存款是按照复利的方式计算利息的，即把前一期的利息与本金加在一起作为本金，再计算下一期的利息。假设最开始的本金为a元，每期的利率为r，存x期后本息和为f（x）元。至少要经过多少期，本息和才能不小于本金的2倍？”求解的最后，教师指出：银行业经常使用“70原则”，因为ln 2≈0.69315，并且当r比较小时ln（1+r）≈r，所以大约要经过70/100r期（假设年利率为5%，则为14年），本息和才能倍增。这时，学生提问：为什么当r比较小时ln（1+r）≈r？这是解决实际问题经常使用的近似方法，并且对学生理解对数函数、幂函数之间的关系以及对数函数的运算这些大概念很有帮助。因此，教师从函数图像平移到函数y=ln（1+x）在原点处的切线是y=x进行分析，让学生看到近似的合理性。

参考文献：

[1] 卡尔·波普尔.猜想与反驳——科学知识的增长[M].傅季重，纪树立，周昌忠，等译.上海：上海译文出版社，2001.

[2] 李刚，吕立杰.国外围绕大概念进行课程设计模式探析及其启示[J].比较教育研究，2018（9）.

[3] 格兰特·威金斯，杰伊·麦克泰格.追求理解的教学设计（第二版）[M].閆寒冰，宋雪莲，赖平，译.上海：华东师范大学出版社，2017.

[4] 戴维·珀金斯.为未知而教，为未来而学[M].杨彦捷，译.杭州：浙江人民出版社，2015.

[5] 夏繁军，张鹤.“整章—单元—课时”的教学设计及反思——以人教B版第十一章第3单元“空间中的平行关系”为例[J].中学数学教学参考，2021（1）.

[6] 夏繁军.话说“基底”[J].中小学数学（高中版），2013（10）.

[7] 唐恒钧，张维忠.数学问题链教学的内涵与特征[J].教育研究与评论（中学教育教学），2021（1）.

[8] 段志贵，张雯，沈桂如.“设问诱思”：数学课堂教学的有效策略[J].教育研究与评论（中学教育教学），2021（8）.

[9] 李祎，陈柳娟.教学不是一种“告诉”行为[J].教育研究与评论，2021（1）.

*本文系北京市教育科学规划2021年度一般课题“大概念和学习进阶视角下高中数学单元教学实施策略研究”（编号：CDDB21315）的阶段性研究成果。