三角矩阵环上的Gorenstein AC-投射模

牟 婷, 王 淼, 王占平

(1. 西北师范大学 数学与统计学院, 兰州 730070; 2. 绍兴文理学院 数学系， 浙江 绍兴 312000)

1 引言与预备知识

自从Enochs等[1]引入了任意结合环R上Gorenstein投射模的概念以来, 关于任意结合环上Gorenstein同调理论的研究得到广泛关注. 作为Gorenstein投射模的特殊情形, Ding等[2]引入了强Gorenstein平坦模, 文献[3]称其为Ding投射模. 为研究一般环上的稳定模范畴, Bravo等[4]引入了FP∞型模、level模和Gorenstein AC-投射模, 并研究了其同调性质, 这3种模的定义分别为: 如果存在右R-模的正合列

…→Pn→Pn-1→…→P1→P0→M→0,

P·=…→P-1→P0→P1→…,

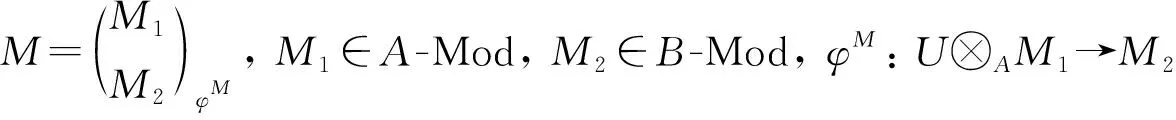
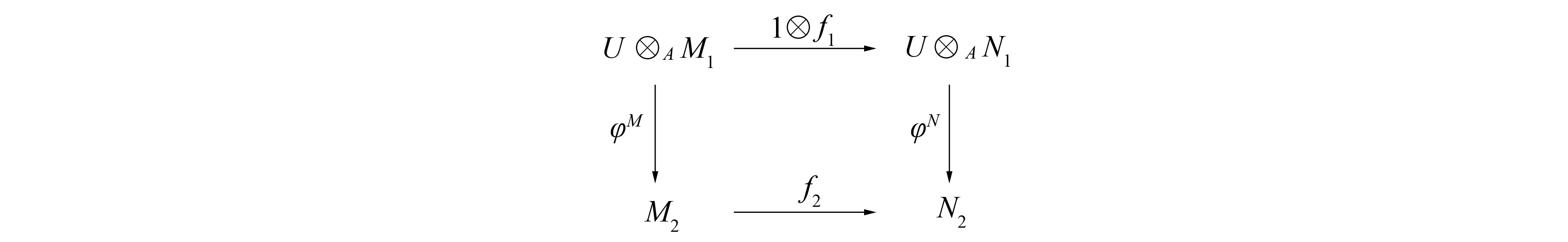
2 Gorenstein AC-投射模

引理1设W=(W1,W2)φW是右T-模, 则:

2)W是有限生成右T-模当且仅当W2是有限生成右B-模, 且CokerφW是有限生成右A-模[11].

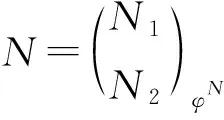
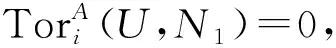
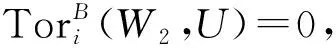
引理3[7]设X·是投射左R-模的正合序列. 若fd(UR)<∞, 则U⊗RX·是正合序列.

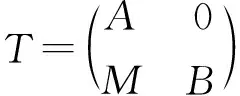
3) 若φL是单同态, CokerφL是level左B-模,L1是level左A-模, 且UA是有限生成投射模, 则L是level左T-模.

证明: 1) 设W1是FP∞型右A-模, 则有右A-模的正合列P·=…→P1→P0→W1→0, 其中每个Pi(i≥0) 是有限生成投射右A-模. 从而有右T-模的正合列…→(P1,0)→(P0,0)→(W1,0)→0. 由引理1知, 每个(Pi,0)(i≥0)是有限生成投射右T-模, 故(W1,0)是FP∞型右T-模. 由L是level左T-模及引理2中1)知,

因此L1是level左A-模.

2) 设W2是FP∞型右B-模, 则有右B-模的正合列Q·=…→Q1→Q0→W2→0, 其中每个Qi(i≥0)是有限生成投射右B-模. 因为BU是平坦模, 所以Q·⊗BU正合. 从而有右T-模的正合列

…→(Q1⊗BU,Q1)→(Q0⊗BU,Q0)→(W2⊗BU,W2)→0.

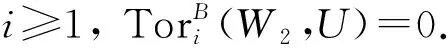
故L2是level左B-模.

3) 因为φL是单同态, 故有左B-模的正合列

从而有左T-模的正合列

设(W1,W2)是FP∞型右T-模, 则有右T-模的正合列

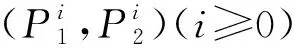
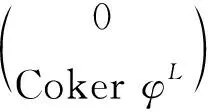
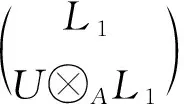
推论1下列结论成立:

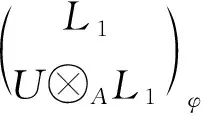
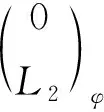
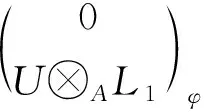
证明: 1) 由引理2中3)知, 结论显然成立.

2) 设(W1,W2)是FP∞型右T-模, 则由引理1知,W2是FP∞型右B-模. 又由L2是level左B-模及引理2中2)知,

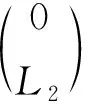
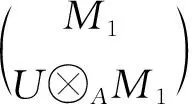
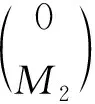
证明: 1) 因为M1是Gorenstein AC-投射左A-模, 则有投射左A-模的正合列

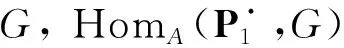
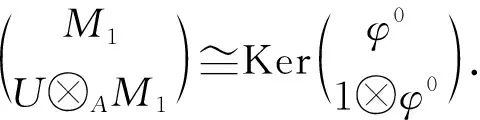
2) 因为M2是Gorenstein AC-投射左B-模, 故有投射左B-模的正合列

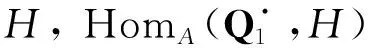
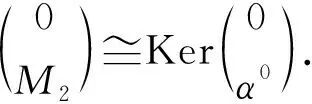
定义1[14]设X是左R-模, 令ld(X)=inf{n∈|存在左R-模的正合列 0→Ln→Ln-1→…→L1→L0→X→0, 使得对所有的i=0,1,…,n,Li是level左R-模}. 称ld(X)为X的level维数. 若这样的n不存在, 则令ld(X)=∞.

证明: 充分性显然成立.

0→HomR(P·,Ln)→…→HomR(P·,L0)→HomR(P·,G)→0.

又因为对所有的i=0,1,…,n, HomR(P·,Li)正合. 再由文献[15]中定理6.3知, HomR(P·,G)正合.

下面给出本文的主要结果.

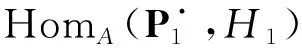
其中

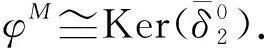
充分性. 因为φM:U⊗AM1→M2是单同态, 所以有左T-模的正合列

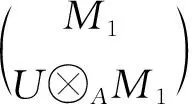
由定理1可得以下推论.

1)M是Gorenstein AC-投射左T(R)-模;

2)M1,CokerφM是GorensteinAC-投射左R-模, 且φM是单同态;

3)M2,CokerφM是Gorenstein AC-投射左R-模, 且φM是单同态.